График силы трения от скорости

Введение

Люди долго жили в неведении и из всего происходящего, из любого природного процесса, люди, ведомые инстинктами, либо извлекали или пытались извлечь пользу, либо опасались и прятались.

Много позже, когда люди стали куда умнее, развились и овладели элементарными навыками и, возможно, знаниями, они пытались узнать больше о том или ином явлении, пытались истолковать его по-другому, кроме как, приписывая любое дуновение ветерка к воле божьей.

По большей части изучали мир астрономы и просто одарённые, кому устройство мира было интересно. Они и положили начало развитию науки и принесли в мир первые знания, которые мы теперь используем в своих целях. Примечательно то, что сегодня, за всего один день, человек узнаёт больше, чем 200 лет тому назад, человек узнавал за всю свою жизнь.

Сила трения и ее физическая природа

Сила трения в природе и технике изучается в 7 классе.

Например, когда вы пытаетесь толкнуть шкаф по полу, трение затрудняет это. Сила трения всегда действует в направлении, противоположном скольжению.

Величина трения зависит от материалов, из которых изготовлены две поверхности. Чем грубее поверхность, тем больше возникает трения.

Иногда мы хотим уменьшить силу трения. Для этого можно использовать антифрикционное масло для уменьшения трения между движущимися частями внутри автомобильного двигателя. Такое масло разделяет поверхности и может течь между ними. Уменьшенное трение означает меньший износ движущихся частей автомобиля и меньшее выделение тепла.

Формула силы трения

Трение равно приложенной силе, которая стремится переместить тело в состоянии покоя. Трение увеличивается по мере приложения силы. У него есть определенное максимальное значение. Трение не увеличивается сверх этого значения.

Формула коэффициента трения:Максимальное значение трения известно как сила предельного трения (Fs). Это зависит от нормальной силы (силы нажатия) между двумя контактирующими поверхностями. Соотношение между силой предельного трения Fs и нормальной реакцией поверхности R является постоянным. Эта постоянная называется коэффициентом трения и представлена μ.

Коэффициент трения:

Сила трения и ее виды

Прежде чем перейти к ответу на вопрос, от чего зависит коэффициент трения, следует рассмотреть собственно само явление и его виды.

Каждый человек интуитивно понимает, что любой вид трения предполагает наличие физического контакта минимум двух поверхностей. Это могут быть твердые, жидкие и газообразные среды.

Трение между твердыми телами делится на три вида. Самой большой силой обладает так называемое трение покоя. Многие замечали, что для смещения шкафа или короба, стоящего на полу, необходимо приложить некоторую силу. Величина, которая препятствует этому смещению, называется трением покоя.

Следующий вид — скольжения. По абсолютной величине оно, как правило, на 10-30 % меньше проявляет себя, когда два тела скользят друг по другу. Например, движение конькобежца или лыжника возможны благодаря небольшому значению трения скольжения. В то же время скользить в ботинках по асфальту нельзя из-за значительной силы трения.

Трение качения действует, когда тело с круглой поверхностью катится по некоторой плоскости. Например, движение шарика или ролика в подшипнике или колеса по дороге. В ряде случаев величина трения качения на один-два порядка меньше, чем трения скольжения.

Любые перемещения в жидкостях и газах также сопровождаются появлением трения. В отличие от предыдущих видов, трение в текучих субстанциях зависит от скорости перемещения объекта в них.

Важно понимать, что какой бы вид трения ни рассматривался, соответствующая сила всегда препятствует механическому движению

Сила вязкого трения

Существуют определенные закономерности, которым подчинены и силы трения и сопротивления среды с условным обозначением суммарной силы силой трения. Ее величина находится в зависимости от:

формы и размеров тела;
состояния его поверхности;
скорости относительно среды и ее свойства, называемого вязкостью.

Для изображения зависимости силы трения от скорости тела по отношению к среде используют график рисунка 1 .

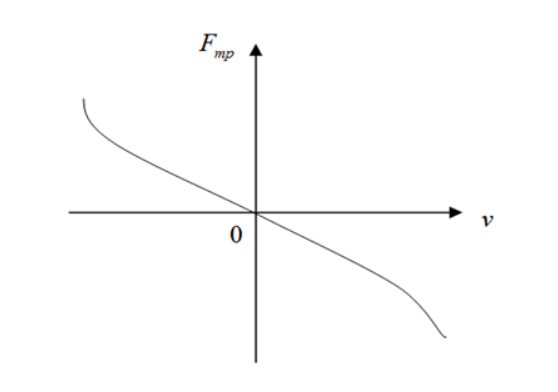
Рисунок 1 . График зависимости силы трения от скорости по отношению к среде

Если значение скорости мало, то сила сопротивления прямо пропорциональна относительно υ , а сила трения линейно увеличивается со скоростью:

F т р = — k 1 υ ( 1 ) .

Наличие минуса означает направление силы трения в противоположную сторону относительно направления скорости.

При большом значении скорости происходит переход линейного закона в квадратичный, то есть рост силы трения пропорционально квадрату скорости:

F т р = — k 2 υ 2 ( 2 ) .

Если в воздухе уменьшается зависимость силы сопротивления от квадрата скорости, говорят о скоростях со значениями нескольких метров в секунду.

Величина коэффициентов трения k 1 и k 2 находится в зависимости от формы, размера и состояния поверхности тела и вязких свойств среды.

Если рассматривать затяжной прыжок парашютиста, то его скорость не может постоянно увеличиваться, в определенный момент начнется ее спад, при котором сила сопротивления приравняется к силе тяжести.

Значение скорости, при котором закон ( 1 ) производит переход в ( 2 ) , зависит от тех же причин.

Происходит падение двух различных по массе металлических шариков с одной и той же высоты с отсутствующей начальной скоростью. Какой из шаров упадет быстрее?

Дано: m 1 , m 2 , m 1 > m 2

Решение

Во время падения оба тела набирают скорость. В определенный момент движение вниз производится с установившейся скоростью, при которой значение силы сопротивления ( 2 ) приравнивается силе тяжести:

F т р = k 2 υ 2 = m g .

Получаем установившуюся скорость по формуле:

Следовательно, тяжелый шарик обладает большей установившейся скоростью падения, чем легкий. Поэтому достижение земной поверхности произойдет быстрее.

Ответ: тяжелый шарик быстрее достигнет земли.

Парашютист летит со скоростью 35 м / с до раскрытия парашюта, а после – со скоростью 8 м / с . Определить силу натяжения строп при раскрытии парашюта. Масса парашютиста 65 к г , ускорение свободного падения 10 м / с 2 . Обозначить пропорциональность F т р относительно υ .

Дано: m 1 = 65 к г , υ 1 = 35 м / с , υ 2 = 8 м / с .

Найти: T — ?

Решение

Перед раскрытием парашютист обладал скоростью υ 1 = 35 м / с , то есть его ускорение было равным нулю.

По второму закону Ньютона получаем:

После того, как парашют раскрылся, его υ меняется и становится равной υ 2 = 8 м / с . Отсюда второй закон Ньютона примет вид:

0 — m g — k υ 2 — T .

Для нахождения силы натяжения строп необходимо преобразовать формулу и подставить значения:

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: силы в механике, сила трения, коэффициент трения скольжения.

Сила трения — это сила взаимодействия между соприкасающимися телами, препятствующая перемещению одного тела относительно другого. Сила трения всегда направлена вдоль поверхностей соприкасающихся тел.

В школьной физике рассматриваются два вида трения.

1.Сухое трение. Оно возникает в зоне контакта поверхностей твёрдых тел при отсутствии между ними жидкой или газообразной прослойки. 2.Вязкое трение. Оно возникает при движении твёрдого тела в жидкой или газообразной среде или при перемещении одного слоя среды относительно другого.

Сухое и вязкое трение имеют разную природу и отличаются по свойствам. Рассмотрим эти виды трения по отдельности.

Примеры измерений в различных условиях

Коэффициент трения скольжения может быть измерен в различных условиях и относительно разных пар поверхностей. Рассмотрим несколько примеров измерений в различных ситуациях:

Измерение коэффициента трения скольжения на металле

Для измерения коэффициента трения скольжения на металлической поверхности можно использовать специальные испытательные устройства. При этом одна поверхность устанавливается на вертикальной платформе, а на нее наносится металлическая пластина. После этого на пластину надавливают силой и начинают постепенно повышать силу, пока не наступит скольжение. Путем измерения силы и угла наклона пластины можно получить значение коэффициента трения скольжения.
Измерение коэффициента трения скольжения на разных поверхностях

Чтобы измерить коэффициент трения скольжения на различных поверхностях, можно воспользоваться методом наклона двух тел. Для этого одно тело устанавливают на наклонной плоскости, а на него наносят второе тело. Наклон плоскости увеличивается, пока не наступит скольжение. Путем измерения угла наклона и силы, необходимой для вызова скольжения, можно определить коэффициент трения скольжения на этих поверхностях.
Измерение коэффициента трения скольжения при использовании смазки

Для измерения коэффициента трения скольжения при использовании смазочных материалов, используются специальные испытательные стенды. На эти стенды устанавливаются испытательные пары, которые смазываются различными смазками. Затем на пары наносится сила, и измеряется сила скольжения. Путем деления силы скольжения на приложенную силу можно получить значение коэффициента трения скольжения при использовании разных смазочных материалов.

Примеры измерений коэффициента трения скольжения в различных условиях демонстрируют, что этот показатель может быть определен для разных материалов и условий эксплуатации. Измерение коэффициента трения скольжения является важным заданием для многих инженеров и специалистов, так как позволяет оценить свойства трения материалов и выбрать оптимальные смазочные материалы.

Разновидности силы трения

При условии наличия относительного движения двух контактирующих между собой тел, возникающие в таком процессе силы трения подразделяются на такие виды:

Трение скольжения (представляет силу, возникающую как следствие поступательного перемещения одного из взаимодействующих тел относительно второго и воздействующая на данное тело в направлении, которое будет противоположным направлению скольжения).
Трение качения (представляет момент сил, способный возникать в условиях процесса качения одного из двух контактирующих с другим тел).
Трение покоя (считается силой, возникающей между двумя взаимодействующими телами, при этом она становится серьезным препятствием для возникновения относительного движения. Такая сила преодолевается с целью приведения данных контактирующих тел в движение относительно друг друга. Такой вид трения появляется при микроперемещениях (к примеру, при деформации) контактирующих тел. При возрастании усилий начнется повышение и силы трения.
Трение верчения (является моментом силы, возникающим между контактирующими телами в условиях вращения одного из них в отношении другого и направленным против вращения). Определяется формулой: $M=pN$, где $N$ — нормальное давление, $p$- коэффициент трения верчения, имеющий размерность длины.

Экспериментальным образом была установлена независимость силы трения от площади поверхности, вдоль которой наблюдается соприкосновение тел, и пропорциональность силе нормального давления, с которой одно тело будет действовать на второе.

Определение 2

Постоянная величина представляет коэффициент трения, при этом зависимый от природы и состояния трущихся поверхностей.

В определенных ситуациях трение оказывается полезным. Можно привести примеры с невозможностью хождения человека (при отсутствии трения) и движением автотранспорта. Наряду с тем, трение может оказывать и вредный эффект. Так, оно провоцирует износ соприкасающихся деталей механизмов, дополнительный расход топлива для транспортных средств. Средством противостояния этому служат различные смазки (воздушные или жидкостные подушки). Еще одним эффективным способом считается замена скольжения качением.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При измерении коэффициента трения брусок перемещали но горизонтальной поверхности стола и получили значение силы трения $ F_1 $. Затем на брусок положили груз, масса которого в 2 раза больше массы бруска, и получили значение силы трения $ F_2 $. При этом сила трения $ F_2 $

1) равна $ F_1 $
2) в 2 раза больше $ F_1 $
3) в 3 раза больше $ F_1 $
4) в 2 раза меньше $ F_1 $

2. В таблице приведены результаты измерений силы трения и силы нормального давления при исследовании зависимости между этими величинами.

Закономерность $ \mu=N/F_{тр} $ выполняется для значений силы нормального давления

1) только от 0,4 Н до 2,0 Н
2) только от 0,4 Н до 3 Н
3) только от 0,4 Н до 4,5 Н
4) только от 2,0 Н до 4,5 Н

3. При измерении силы трения брусок перемещали по горизонтальной поверхности стола и получили значение силы трения $ F_1 $. Затем брусок перемещали, положив его на стол гранью, площадь которой в 2 раза больше, чем в первом случае, и получили значение силы трения $ F_2 $. Сила трения $ F_2 $

1) равна $ F_1 $
2) в 2 раза больше $ F_1 $
3) в 2 раза меньше $ F_1 $
4) в 4 раза меньше $ F_1 $

4. Два деревянных бруска массой $ m_1 $ и $ m_2 $ скользят по горизонтальной одинаково обработанной поверхности стола. На бруски действует сила трения скольжения $ F_1 $ и $ F_1 $ соответственно. При этом известно, что $ F_2=2F_1 $. Следовательно, $ m_1 $

1) $ m_1 $
2) $ 2m_2 $
3) $ m_2/2 $
4) ответ зависит от значения коэффициента трения

5. На рисунке приведены графики зависимости силы трения от силы нормального давления. Сравните значения коэффициента трения.

1) $ \mu_2=\mu_1 $
2) $ \mu_2>\mu_1 $
3) $ \mu_2<\mu_1 $
4) $ \mu_2>>\mu_1 $

6. Учащийся выполнял эксперимент по измерению силы трения, действующей на два тела, движущихся по горизонтальным поверхностям. Масса первого тела $ m_1 $, масса второго тела $ m_2 $, причем $ m_1 =2m_2 $. Он получил результаты, представленные на рисунке в виде диаграммы. Какой вывод можно сделать из анализа диаграммы?

1) сила нормального давления $ N_2=2N_1 $
2) сила нормального давления $ N_1=N_2 $
3) коэффициент трения $ \mu_1=\mu_2 $
4) коэффициент трения $ \mu_2=2\mu_1 $

7. Два автомобиля одинаковой массы движутся один но асфальтовой дороге, а другой — по грунтовой. На диаграмме приведены значения силы трения для этих автомобилей. Сравните значения коэффициента трения ($ \mu_1 $ и $ \mu_2 $).

1) $ \mu_2=0.3\mu_1 $
2) $ \mu_2=\mu_1 $
3) $ \mu_2=1.5\mu_1 $
4) $ \mu_2=3\mu_1 $

8. На рисунке приведён график зависимости силы трения от силы нормального давления. Чему равен коэффициент трения?

1) 0,5
2) 0,2
3) 2
4) 5

9. Санки весом 3 кг скользят по горизонтальной дороге. Сила трения скольжения их полозьев о дорогу 6 Н. Чему равен коэффициент трения скольжения полозьев о дорогу?

1) 0,2
2) 0,5
3) 2
4) 5

10. При движении тела массой 40 кг по горизонтальной поверхности действует сила трения скольжения 10 Н. Какой станет сила трения скольжения при уменьшении массы тела в 5 раз?

1) 1 Н
2) 2 Н
3) 4 Н
4) 5 Н

11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при увеличении массы бруска, движущегося по столу. В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила трения
Б. Коэффициент трения
B. Сила нормального давления

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Сила трения покоя больше приложенной к телу силе.
2) Сила трения качения меньше силы трения скольжения при той же массе тела.
3) Коэффициент трения скольжения прямо пропорционален силе нормального давления.
4) Сила трения зависит от площади опоры движущегося тела при одинаково обработанной его поверхности.
5) Максимальная сила трения покоя равна силе трения скольжения.

Часть 2

13. Автомобиль, имея скорость 72 км/с, начинает тормозить с выключенным двигателем и проходит путь 100 м. Чему равны ускорение автомобиля и время торможения?

Дополнительные примеры по коэффициенту трения

Чтобы повысить вашу компетентность в решении задач на коэффициент трения, вот еще несколько примеров.

Блок массой $10\, \text{kg}$ помещен на стол и опирается с противоположных сторон на две пружины, прикрепленные к массе $5\, \text{kg}$ и $12\, \text{kg}$ соответственно. Если блоки и стол имеют стандартный коэффициент трения $0.4$, найдите ускорение и напряжение в пружинах.

Решение:

Составьте диаграмму, чтобы иметь более четкое представление о том, о чем идет речь в вопросе.

Рис. 9. Определение натяжения пружин с помощью коэффициента трения.

Теперь вам нужно определить силы, действующие на объект на столе, и обозначить их диаграммой

Здесь нужно быть очень внимательным, обратите внимание, что поскольку масса $12\, \text{kg}$ будет тянуть с большей силой, чем масса $5\, \text{kg}$, то объект, скорее всего, будет двигаться вправо

Однако эта ваша гипотеза зависит от того, превышает ли сила силу трения, иначе объект останется неподвижным на столе.

Следовательно, сила трения действует вправо, чтобы предотвратить натяжение, создаваемое $12\, \text{kg}$ массой.

Рис. 10. Иллюстрация сил, действующих на тело, притянутое пружинами, прикрепленными к массам.

Из приведенной выше диаграммы вы поймете, что происходит в каждой точке.

Не волнуйтесь, просто начните с крайних точек, левой или правой, и продолжайте анализировать действие сил, пока не дойдете до противоположного конца.

Из крайнего левого положения видно, что масса $5\, \text{kg}$ прикладывает силу вниз, $49\, N$, но система над ней вызывает напряжение, $T_2$, которое стремится переместить массу вверх с ускорением $a$. Таким образом, это можно выразить как

Это происходит потому, что в итоге масса $5\, \text{kg}$ подтягивается и движется с ускорением, $a$.

Теперь, что касается предмета на столе, вы заметите, что напряжение $T_2$ стремится притянуть предмет влево. Кроме того, сила трения действует влево, поскольку она пытается препятствовать движению вправо, вызванному напряжением $T_1$, действующим вправо. Это выражается как

Это происходит потому, что после того, как две силы, направленные влево (т.е. $T_2$ и $F$), попытались преодолеть силу, направленную вправо $T_1$, и потерпели неудачу, ожидается, что объект массой $10\, \text{kg}$ будет двигаться вправо с ускорением $a$.

Если посмотреть на третью массу, расположенную слева, то можно заметить, что она прикладывает силу $117.6\, \text{N}$, направленную вниз, и ей противодействует натяжение пружины вверх, $T_1$. Таким образом, это можно выразить как

Поскольку предполагается, что сила, приложенная вниз $117.6\, \text{N}$, должна преодолеть силу натяжения $T_1$, то масса $12\, \text{kg}$ должна двигаться с ускорением $a$.

Теперь у нас есть три уравнения из объясненных выше.

Эти три уравнения таковы:

Суммируем все 3 уравнения, следовательно, \ что дает

Обратите внимание, что

тогда,

Поэтому подставим значение $F$ в уравнение и получим

Разделите обе стороны на 27, чтобы найти ускорение, $a$, как

Чтобы определить натяжение пружин, $T_1$ и $T_2$, мы подставим в ранее приведенные уравнения.

Вспомните, что

Поэтому,

это даёт

Добавьте $49\, \text{N}$ к обеим сторонам уравнения, чтобы получить наше напряжение, $T_2$, как

Вспомните, что

и $F$ — $39.2\, \text{N}$, $a$ — $1.09\, \text{ms}^{-2}$ и $T_2$ — $54.45\, \text{N}$.

Следовательно, подставьте в уравнение

что даёт

Добавьте $93.65\, \text{N}$ к обеим сторонам уравнения, чтобы получить наше напряжение, $T_1$, как

Человек стоит неподвижно на склоне горы, и коэффициент трения между подошвой его ноги и поверхностью горы равен $0.26$. Если в следующем году произошло извержение вулкана, которое увеличило коэффициент трения между подошвой его ноги и горой на $0.34$, на какой угол увеличился или уменьшился склон горы?

Решение:

Чтобы определить угол, образуемый склоном горы, вспомним, что \

Следовательно, текущий склон горы имеет угол

Возьмите обратную величину, чтобы найти $\theta$

Следовательно, текущий склон горы имеет угол \.

Однако через год после этого на горе произошло извержение, которое увеличило коэффициент трения на $0.34$. Таким образом, новый коэффициент трения равен

что даёт

Нам нужно определить новый угол наклона горы, используя

Таким образом,

Возьмите обратную величину, чтобы найти $\theta$

Следовательно, новый склон горы имеет угол

Склон горы имел прежний угол $14.57°$, но после извержения он увеличился до $30.96°$.

Поэтому извержение увеличило угол между склонами горы на $16.39°$.

Определение силы трения

Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.

Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.

Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел. Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.

Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.

Виды силы трения

В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.

Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:

трение скольжения,
трение покоя,
трение качения.

Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.

Практическое применение коэффициента трения скольжения

Коэффициент трения скольжения является важным параметром при решении задач, связанных с движением тел. Он находит широкое применение в различных областях науки и техники.

Одной из основных областей, где применяется коэффициент трения скольжения, является машиностроение. Если мы знаем коэффициент трения скольжения между двумя соединенными деталями, мы можем рассчитать силы, которые действуют на эти детали. В результате этого можно предотвратить повреждение и износ деталей, увеличить их срок службы и улучшить эффективность работы механизмов.

Также коэффициент трения скольжения применяется в автомобильной промышленности. Знание коэффициента трения скольжения между шинами автомобиля и дорожным покрытием позволяет оптимизировать тормозные системы и повысить безопасность движения. Кроме того, он учитывается при разработке шин с максимальным сцеплением, что позволяет улучшить управляемость автомобиля и снизить расход топлива.

Другим практическим применением коэффициента трения скольжения является строительство. Знание коэффициента трения скольжения между различными материалами позволяет определить максимальный наклон, на котором возможно строительство склонов, поверхностей с высоким коэффициентом трения. Это позволяет предотвратить срыв земляных масс и обеспечить безопасность на строительной площадке.

Также коэффициент трения скольжения используется в металлургической и химической промышленности. Знание этого коэффициента позволяет правильно рассчитать силы трения между материалами при их перемещении или смешивании, что обеспечивает безопасность производственных процессов и предотвращает аварии и разливы опасных веществ.

Таким образом, коэффициент трения скольжения имеет широкое практическое применение в различных областях науки и техники. Знание этого параметра позволяет оптимизировать работу механизмов, повысить безопасность и эффективность процессов и предотвращать аварии и повреждения оборудования.

Независимость от площади [ править | править код ]

Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой. На самом деле, площадь соприкосновения, казалось бы, ровных поверхностей может находиться в пределах 0 , 01 % − 0 , 001 % <displaystyle 0,01\%-0,001\%> от всей мнимой площади соприкосновения. А в случае поверхностей максимально гладких начинает возникать межмолекулярное притяжение.

Обычно это демонстрируется примером:

Два цилиндра из мягких металлов соединяют плоскими частями, а затем с легкостью отрывают. После этого два цилиндра соединяют и немного двигают относительно друг друга. При этом все неровности поверхности притираются друг к другу, образуя максимальную площадь соприкосновения: появляются силы межмолекулярного притяжения. А после разъединить эти два цилиндра становится очень сложно.

Коэффициент трения

Когда он качал кресло-качалку, слушая «2 rocking chairs» Джона Беллиона, его осенило: «Что будет, если это кресло никогда не перестанет качаться?». «Как насчет двигателей в машинах, представьте, что они работают бесконечно, никогда не останавливаясь. Эврика! Я нашел это», — закричал мистер Финики Спинс в восторге и сказал: «Всему нужен тормоз, чтобы не сломаться. Мы применяем тормоза, чтобы передохнуть, отсюда трение». InВ этом увлекательном путешествии вы узнаете об уравнении, формуле, устройстве для измерения, а также о единицах измерения коэффициента трения. Давайте качаться, не ломаясь!

Задачи на Движение под действием силы трения

Тренировочные задания для подготовки к контрольным,
самостоятельным и диагностическим работам по теме
«ЗАДАЧИ на Движение под действием силы трения» + Решения

Модуль силы трения скольжения можно определить по формуле: F_тр = µN, где µ — коэффициент трения, N— модуль силы нормального давления (и силы реакции опоры). Максимальная сила трения покоя: (F_тр)_мах = µN. При одинаковых условиях сила трения скольжения намного больше силы трения качения. Вектор силы трения скольжения всегда направлен противоположно вектору скорости тела. Коэффициент трения можно определить по формуле: µ = F_тр/N. Это величина безразмерная.

Если на тело действует только сила трения, то такое тело движется равнозамедленно до остановки. Расстояние, которое тело проходит до остановки, называют тормозным путем. Обозначают буквой l. Время торможения — время, нужное для остановки.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Автомобиль массой 5 т движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен 0,03. Определите силу тяги, развиваемую двигателем.

ОТВЕТ: F_тяги = 1470 Н.

РЕШЕНИЕ:

Задача № 2.
Сани со стальными полозьями перемещают равномерно по льду, прилагая горизонтальное усилие 2 Н. Каков вес саней?

ОТВЕТ: Вес саней 100 Н.

Задача № 3.
Деревянный брусок массой 3 кг тянут по горизонтальной деревянной доске с помощью пружины. Коэффициент трения равен 0,3. Найти удлинение пружины, если ее жесткость 10 кН/м.

ОТВЕТ: Удлинение пружины 0,09 см.

Задача № 4.
Велосипедист, ехавший со скоростью 36 км/ч, увидел примерно в 10 м от себя препятствие и резко затормозил. Успеет ли велосипедист остановиться до препятствия?

ОТВЕТ: Велосипедист успеет остановиться до препятствия, так как S = 10 м (расстояние до препятствия), а тормозной путь велосипедиста ≈ 7 м. Если скорость движения возрастет вдвое, то тормозной путь увеличится в 4 раза.

Задача № 5.
Автомобиль движется со скоростью 10 м/с по гладкой горизонтальной дороге. Пройдя с выключенным мотором расстояние 150 м, автомобиль останавливается. Сколько времени автомобиль двигался с выключенным мотором и каков коэффициент трения при его движении?

ОТВЕТ: t = 30 с; µ = 0,033.

ЗАДАЧИ на Движение под действием силы трения

Задача № 6.
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определить величину силы сопротивления.

ОТВЕТ: F_тp= 15 Н.

Задача № 7.
Тело скользит равномерно по наклонной плоскости с углом наклона 30°. Определите коэффициент трения тела о плоскость.

ОТВЕТ: µ ≈ 0,58.

Задача № 8.
С какой наибольшей скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 80 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикального положения он при этом отклоняется?

ОТВЕТ: v_мах = 17,7 м/с = 64 км/ч — наибольшая скорость движения; a ≈ 22°.

Задача № 9.
Шофер грузовика, едущего со скоростью 72 км/ч, заметил на дороге знак. Сможет ли он, не сбавляя скорости, проехать поворот, если его радиус равен 25 м? Считать коэффициент трения шин о дорогу 0,4.

ОТВЕТ: Шофер должен уменьшить скорость движения, так как радиус окружности, которую опишет грузовик при данной скорости, 100 м, а радиус поворота — 25 м. В противном случае грузовик занесет на обочину дороги.

Дополнительный материал для решения задач

Конспект урока по физике «ЗАДАЧИ на Движение под действием силы трения с решениями». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:

Вернуться к Списку конспектов по физике для 7-11 классов
Найти конспект через Кодификатор ОГЭ по физике
Найти конспект через Кодификатор ЕГЭ по физике

Классификация коэффициента трения

В физике существует несколько видов коэффициента трения, которые классифицируются по условиям, в которых возникает трение. Рассмотрим основные типы коэффициента трения:

Статический коэффициент трения

Статический коэффициент трения обозначается как μ_ст. Он характеризует силу трения между двумя неподвижными поверхностями. Этот коэффициент определяет минимальную силу, необходимую для начала движения одной поверхности относительно другой.

Кинетический коэффициент трения

Кинетический коэффициент трения обозначается как μ_к. Он характеризует силу трения между движущимися поверхностями. Этот коэффициент определяет силу трения при постоянной скорости движения.

Кроме того, в зависимости от приложенной силы и условий трения, коэффициенты трения могут быть различными. Например, коэффициент трения может зависеть от состояния поверхностей, их материала, размеров и т.д. Поэтому при изучении трения необходимо учитывать все факторы, влияющие на его характеристики.