Основные понятия теории графов

ВВЕДЕНИЕ

Среди жителей Кёнигсберга была распространена такая практическая головоломка: можно ли пройти по всем мостам через реку Преголя, не проходя ни по одному из них дважды? В 1736 году выдающийся математик Леонард Эйлер заинтересовался задачей и в письме другу привел строгое доказательство того, что сделать это невозможно. В том же году он доказал замечательную формулу, которая связывает число вершин, граней и ребер многогранника в трехмерном пространстве. Формула таинственным образом верна и для графов, которые называются «планарными». Эти два результата заложили основу теории графов и неплохо иллюстрируют направление ее развития по сей день. Граф как математический объект оказался полезным во многих теоретических и практических задачах. Наверное, дело в том, что сложность его структуры хорошо отвечает возможностям нашего мозга: это структура наглядная и понятно устроенная, но, с другой стороны, достаточно богатая, чтобы улавливать многие нетривиальные явления.

Побывав в зимней математической школе при МФТИ, я узнала о небольшой, но в то же время сложной олимпиадной теме. Речь идет о теме “Двудольные графы”. Времени на нее уделялось относительно немного, и я решила изучить ее более подробно самостоятельно.

Актуальность. Данная тема актуальна, так как такие задачи могут встретиться в олимпиадах различного уровня. Но, к сожалению, школьная математика не предусматривает решения задач на двудольные графы. Некоторые дети заинтересованы в том, чтобы поступить в университеты с помощью олимпиад, таким образом, я попыталась собрать всю информацию по данной теме в своем проекте. Стоит заметить, что решение задач на эту тему, развивает логику.

Объектом исследования является процесс изучения темы “Двудольные графы”.

Предмет исследования – возможность применения полученных знаний.

Цель исследования – рассмотреть и овладеть знаниями о теме “Двудольные графы”.

В процессе работы я поставила перед собой следующие задачи :

Разобрать всевозможную теорию по теме “Двудольные графы”;
Собрать в своем проекте различные задачи на данную тему.

Связанные определения[править | править код]

Дерево с отмеченной вершиной называется корневым деревом.
- m{\displaystyle m}-й ярус дерева T{\displaystyle T} — множество узлов дерева, на уровне m{\displaystyle m} от корня дерева.
- на вершинах: u≺v{\displaystyle u\prec v}, если вершины u{\displaystyle u} и v{\displaystyle v} различны и вершина u{\displaystyle u} лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной v{\displaystyle v}.
- корневое поддерево с корнем v{\displaystyle v} — подграф {v}∪{w∣v<w}{\displaystyle \{v\}\cup \{w\mid v<w\}}.
- В контексте, где дерево предполагается имеющим корень, дерево без выделенного корня называется свободным.

Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:

уровень корня дерева T{\displaystyle T} равен 0;
уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева T{\displaystyle T}, содержащего данный узел.

Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

Несводимым называется дерево, в котором нет вершин степени 2.

Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
Центроид — вершина, при удалении которой размеры получившихся компонент связности не превышают n2{\displaystyle {\dfrac {n}{2}}} (половины размера исходного дерева)

Удаление вершины

В некоторых задачах требуется выполнить удаление заданной вершины v из дерева (предположим, что f — отец удаляемой вершины).

Задача удаления достаточно проста и выполняется за константное время, если у удаляемой вершины v не более одного поддерева (предположим, что если поддерево у вершины v существует, то w — его корень). В этом случае можно выполнить непосредственное удаление вершины v, после чего выполняются следующие действия:

если v — корень дерева, то корнем дерева станет вершина w (если у вершины v сыновей не было, то дерево перестанет существовать);
если v — лист, то ссылка у вершины f, указывающая на вершину v, станет пустой;
если v не лист и не корень дерева, то ссылка у f, указывающая на v, будет указывать на w.

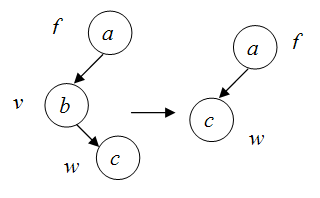
Случай удаления вершины v, у которой два поддерева, можно свести к предыдущему. При этом непосредственного удаления вершины v из дерева не происходит, а ключ вершины v заменяется на значение минимального (максимального) ключа среди вершин правого (левого) поддерева вершины v — такое удаление называют правым (левым).

Рассмотрим более подробно правое удаление. Предположим, что минимальный ключ в правом поддереве вершины v имела вершина z. Запишем ключ вершины z в вершину v, что приведёт к тому, что в дереве появятся две вершины v и z с одинаковыми ключевыми значениями, а это недопустимо для бинарного поискового дерева.

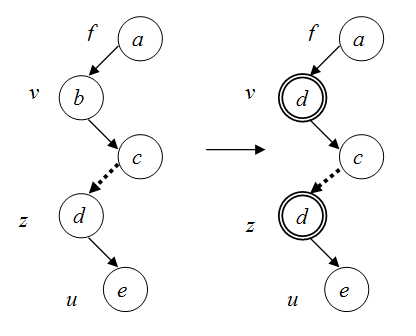
Поэтому, удаляем вершину z из дерева. Это сделать проще, так как вершина z не имеет левого поддерева (возможно, является листом) и завершаем процедуру удаления.

Деревья

Дерево — это связный неориентированный граф без циклов.

Пример дерева

Свойства дерева:

У дерева с хотя бы 2 вершинами всегда есть висячая вершина — вершина степени 1.

Действительно, если начать из любой вершины идти по непосещенным ранее вершинам, то в какой-то момент мы прекратим это делать, ведь граф конечный. При этом если из этой вершины не может быть ребер в непосещенные вершины — ведь тогда прекращать рано, и не может быть ребер в посещенные ребра (помимо предыдущей) — ведь тогда есть цикл. А значит, есть ребро только в предыдущую вершину, значит степень равна 1.

У дерева с хотя бы 2 вершинами всегда есть две висячие вершины.

Действительно, если предыдущий алгоритм начать из висячей вершины, то мы уткнемся в другую висячую вершину.

У дерева с $N$ вершинами всегда ровно $N-1$ ребро.

Давайте отрезать от дерева его висячие вершины — при этом число вершин уменьшится на один, число ребер тоже уменьшится на один, а граф останется деревом. Раз граф остается деревом, у него все время будет висячая вершина, пока $N > 1$. В какой-то момент останется только одна вершина и ноль ребер. Раз мы отрезали столько же вершин, сколько ребер, и получили 1 вершину и 0 ребер, значит изначально вершин было ровно на одну больше.

Между любыми двумя вершинами в дереве есть ровно один простой путь.

Действительно, если их два, то в графе есть цикл. Быть ноль их не может — ведь граф связный.

Дерево — это минимальный по числу рёбер связный граф на $N$ вершинах.

Действительно, если есть связный граф, в котором меньше, чем $N-1$ ребро, то давайте уберем из его цикла ребро. Граф при этом остается связным, а число ребер уменьшается. Давайте повторять это, пока в какой-то момент циклов в графе не будет, а значит осталось дерево. Но мы уже доказали, что в дереве $N-1$ ребро, это противоречие, ведь у нас сначала было меньше ребер, а мы еще и удалили сколько-то.

Поиск циклов в графе

Циклом в графе $G$ называется ненулевой путь, ведущий из вершины $v$ в саму себя. Граф называют ацикличным, если в нем нет циклов.

В обычном dfs мы используем два цвета (1 — вершина посещена, 0 — не посещена), если же нам надо найти цикл, то давайте хранить 3 цвета:

0 — вершина не просмотрена
1 — мы входили DFS-ом в эту вершину, но еще не вышли (а значит из нее есть путь до текущей),
2 — мы входили DFS-ом в эту вершину

Заметим, что цикл будет тогда и только тогда, когда мы пытаемся войти в вершину с цветом 1.

В неориентированном графе также надо дополнительно рассмотреть случай, когда мы идем в предка — это циклом все-таки не считается, для этого нужно отдельно добавить второй аргумент prev, где хранить предыдущую вершину в dfs, и никогда не идти в неё.

Практическое задание

9 задача в контесте на поиск цикла в графе.

#Ссылка на контест

https://informatics.msk.ru/mod/statements/view3.php?id=33377

Свойства

Каждое дерево является двудольным графом. Граф двудольный тогда и только тогда, когда он не содержит циклов нечетной длины. Поскольку дерево вообще не содержит циклов, оно является двудольным.
Каждое дерево является медианным графом.
Каждое дерево со всего счетным числом вершин является плоским граф.
Каждый связный граф G допускает остовное дерево, которое является деревом, содержащим каждую вершину G и чьи ребра являются ребрами G.
Каждый связный граф только с счетное число вершин допускает нормальное остовное дерево (Diestel 2005, Предложение 8.2.4).
Существуют связанные графы с несчетным числом вершин, которые не допускают нормального остовного дерева (Diestel 2005, Предложение 8.5.2).
Каждое конечное дерево с n вершинами и n>1 имеет как минимум две конечные вершины (листья). Это минимальное количество листьев характерно для графов путей ; максимальное число n — 1 достигается только звездчатыми диаграммами. Количество листьев не меньше максимальной степени вершины.
Для любых трех вершин в дереве три пути между ними имеют ровно одну общую вершину (эта вершина называется медианой этих трех вершин).
Каждое дерево имеет центр, состоящий из одной или двух смежных вершин. Центр — это средняя вершина или две средние вершины на каждом самом длинном пути. Аналогично, каждое дерево с n вершинами имеет центроид, состоящий из одной или двух смежных вершин. В первом случае удаление вершины разбивает дерево на поддеревья с числом вершин менее n / 2. Во втором случае удаление ребра между двумя центроидными вершинами разбивает дерево на два поддерева с ровно n / 2 вершинами.

Доказать, что всякое дерево является двудольным графом.

Пожалуйста, используйте IE6/7/8 с плагином MathPlayer, Firefox с установленными математическими шрифтами или Opera 9.5 и выше.

Объявления	Последний пост
	Работодателям и кадровым агентствам: Размещение вакансий	26.03.2008 03:07
	Запущен новый раздел «Задачки и головоломки»	29.08.2019 00:42
	ML Research Engineer, до $8k/мес net	06.09.2023 14:11

26.01.2011 11:42
Дата регистрации:12 лет назад
Доказать, что всякое дерево является двудольным графом.

«Доказать, что всякое дерево является двудольным графом.»

Нужно полное доказательство. Если можно — с примером.

Редактировалось 1 раз(а). Последний 31.01.2011 19:58.

26.01.2011 11:59
Дата регистрации:14 лет назад
Посты: 3 155

1. Граф является двудольным тогда и только тогда, когда он не содержит цикла нечётной длины.2. В дереве нет как четных, так и нечетных циклов.

26.01.2011 12:20
Дата регистрации:15 лет назад
можно и конструктивно

Подвесим дерево за какую-нибудь вершину. Скажем, что это первый этаж. Все вершины, которые смежны с ней, образуют второй этаж. Все нерассмотренные вершины, которые смежны с вершинами второго этажа, поселим на третий этаж и т.д.

А потом вершины с нечетных этажей в одну долю, с четных — в другую.

26.01.2011 12:30
Дата регистрации:12 лет назад

«Граф является двудольным тогда и только тогда, когда он не содержит цикла нечётной длины.»Доказательство этого я нашёл.

«В дереве нет как четных, так и нечетных циклов.»А есть како-либо доказательство этого? Или так и записывается в ответе к заданию?

Прошу прощения, если туплю, но я просто вообще ничего не смыслю в Теории графов.

B-дерево

B-дерево – это структура хранения данных, являющаяся разновидностью дерева поиска. Особенностями В-деревьев является:

сбалансированность,
ветвистость,
отсортированность
логарифмическое O(log n) время работы всех стандартных операций (поиск, вставка, удаление).

Сбалансированность означает, что все листы находятся на одинаковом расстоянии от корня. В отличие от бинарных деревьев В-деревья допускают большое число потомков для любого из узлов. Это свойство называется ветвистостью. Благодаря ветвистости, В-деревья очень удобны для хранения крупных последовательных блоков данных, поэтому такая структура часто находит применение в базах данных и файловых системах.

С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц памяти, то есть каждому узлу дерева соответствует блок памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.

Порядок(m) В-дерева – это максимальное число потомков для любого узла. Кроме узлов в дереве присутствует ещё одна сущность – ключи. Именно в них и содержится вся полезная информация. Каждый узел дерева можно представить в виде упорядоченной последовательности ”потомок1; ключ1; потомок2; ключ2; … потомок(N-1); ключ(N-1); потомокN”

Важно заметить, что ключи располагаются между ссылками на потомков и, таким образом, ключей всегда на 1 меньше. В организации В-дерева можно выделить несколько ключевых правил:

Каждый узел содержит строго меньше m (порядок дерева) потомков.
Каждый узел содержит не менее m/2 потомков.
Корень может содержать меньше m/2 потомков.
У корневого узла есть хотя бы 2 потомка, если он не является листом.
Все листья находятся на одном уровне и содержат только данные (ключи). Но это не значит что ключи находятся только в листьях.

Ключи во внутреннем узле окружены указателями или смещениями записей, отсылающими к ключам, которые либо все больше, либо все меньше окруженного ключа. Например, все ключи, меньшие 22, адресуются левой ссылкой, все большие — правой. Для простоты здесь не показаны адреса записей, связанные с каждым ключом.

B+‍‍ дерево — структура данных на основе B-дерева, сбалансированное n-арное дерево поиска с переменным, но зачастую большим количеством потомков в узле. B+‍‍ дерево состоит из корня, внутренних узлов и листьев, корень может быть либо листом, либо узлом с двумя и более потомками.

Изначально структура предназначалась для хранения данных в целях эффективного поиска в блочно-ориентированной среде хранения — в частности, для файловых систем; применение связано с тем, что в отличие от бинарных деревьев поиска, B+‍‍ деревья имеют очень высокий коэффициент ветвления (число указателей из родительского узла на дочерние, обычно порядка 100 или более), что снижает количество операций ввода-вывода, требующих поиска элемента в дереве.

Построение B+‍‍-дерева может требовать перестройки промежуточной структуры, это связано с тем, что количество ключей в каждом узле (кроме корня) должно быть от t до 2t, где t — степень (или порядок) дерева. При попытке вставить в узел 2t+1-й ключ возникает необходимость разделить этот узел, в качестве ключа-разделителя сформированных ветвей выступает t+1-й ключ, который помещается на соседний ярус дерева. Особым же случаем является разделение корня, так как в этом случае увеличивается число ярусов дерева. Особенностью разделения листа B+‍‍-дерева является то, что он делится на неравные части. При разделении внутреннего узла или корня возникают узлы с равным числом ключей k. Разделение листа может вызвать «цепную реакцию» деления узлов, заканчивающуюся в корне.

Определение дерева

Дерево с типом узлов T — это либо:пустое дерево; либо
некоторая вершина типа T (корень) с конечным числом связанных с ней
отдельных деревьев с типом узлов T, называемых поддеревьями.

Данное определение является рекурсивным. Рекурсия используется в большом
числе алгоритмов работы с деревьями.

Из определения дерева ясно, что линейный список можно рассматривать как
дерево, в котором каждая вершина имеет не более одного поддерева. Поэтому список
иногда назы-вают вырожденным деревом.

Изображение структуры деревьев

Вложенные множества.

Здесь A — корневая вершина; B — корень первого поддерева для A; C — корень
второго поддерева для A.
Вложенные скобки.
( A ( B (D (I), E (J, K, L) ), C (F (O), G (M, N), H (P) ) ) )
Таблица

A

B C

D E F G H

I J K L O M N P

Отступы

Уровни
1	2	3

A
	B
		D
			I
		E
			J
			K
			L
	C
		F
			O
		G
			M
			N
		H
			P

Граф

Дерево — связный граф без циклов. Изображается корнем сверху.

Некоторые определения

Упорядоченное дерево — это дерево, к которого ребра (ветви), исходящие
из каждой вершины, упорядочены. Поэтому следующие два упорядоченных дерева —
разные, отличные друг от друга объекты:

Непосредственный потомок вершины X — вершина Y, находящаяся
непосредственно ниже X и связанная с ним. При этом вершина X является
непосредственным предком Y (X родительская вершина для Y). Например, в
следующем дереве вершины J, K, L являются потомками E, а E для них — предок. В
свою очередь, E является потомком B, а B для нее — предок.

Если вершина не имеет потомков, то ее называют терминальной вершиной
или листом. Нетерминальные вершины (имеющие потомков) называются
внутренними.

Уровень вершины (узла) дерева — удаленность вершины от корня. Уровень
корня равен нулю.

Максимальный уровень вершин в дереве называется высотой или
глубиной дерева.

Пример:

Высота дерева равна 3; листья: B, D, F, G; внутренние вершины: A, C, E.

Число потомков вершины называется степенью вершины. Например, в
следующем дереве

степень E равна 3, степень B — 2, степень D — 1, степени I, J, K, L — 0
(листья всегда имеют степень 0).

Линейный список можно рассматривать как дерево со степенью узлов не выше 1.
Например, список A — B — C — D — E можно представить в виде следующих
вырожденных деревьев:

Двоичные (бинарные) деревья

Двоичное (бинарное) дерево — это упорядоченное дерево со степенью
вершин не вы-ше 2. У каждой вершины такого дерева есть не более 2 поддеревьев,
называемых левым и правым поддеревьями. Примеры:

Дерево выражения (a+b/c)*(d-e*f):
Генеалогическое дерево, где у каждого человека есть отец и мать.

Везде далее будем под термином подразумевать .

Поле info содержит информацию, хранящуюся в вершине, а поля llink и rlink
являются указателями на левое и правое поддерево соответственно. Если у вершины
нет какого-либо из поддеревьев, то соответствующий ему указатель равен nil.

Тогда дерево выражения (a+b/c)*(d-e*f) в памяти будет храниться следующим
образом:

(root — указатель на корень дерева).

Алгоритм построения дерева из n вершин с равномерным их размещением

При заданном числе вершин n минимальная высота дерева будет достигнута, если
на всех уровнях, кроме последнего, помещается максимально возможное число вершин
(на уровне k можно разместить до 2k вершин). Такое дерево называется идеально
сбалансированным.

Если общее число вершин n известно, то для построения идеально
сбалансированного дерева необходимо размещать новые вершины в дереве поровну
слева и справа от каждой вершины. Проще всего записать такой алгоритм, использую
рекурсию:

Взять одну вершину в качестве корня.
Построить таким же способом левое поддерево из nl = n div 2 вершин.
Построить таким же способом правое поддерево из nr = n — nl — 1 вершин.

Функция Tree строит идеально сбалансированное дерево из n вершин и возвращает
ука-затель на корень дерева:

Использование:

Пример работы для 7 узлов A, B, C, D, E, F, G (нарисовать структуру вложенных
рекурсивных вызовов):

Печать дерева на экране начиная со строки номер h

(функция wherex из модуля crt возвращает текущую координату x курсора, а
процедура gotoxy устанавливает курсор в заданную позицию на экране).

(нарисовать структуру вложенных рекурсивных вызовов для дерева из 7
узлов)

Литература

Вирт Н. Алгоритмы и структуры данных: Пер. с англ. — М.: Мир, 1989.
Кнут Д. Искусство программирования для ЭВМ: Т.1: Основные алгоритмы: Пер.
с англ. — М.: Мир, 1976.

Структуры данных во внешней памяти

Кроме оперативной памяти, в компьютере используется внешний носитель, как правило, представляющий собой магнитные диски (или твердотельный накопитель). Хотя диски существенно дешевле оперативной памяти и имеют высокую емкость, они гораздо медленнее оперативной памяти из-за механического построения считывания.

Для того чтобы снизить время ожидания, связанное с механическим перемещением, при обращении к диску выполняется обращение одновременно сразу к нескольким элементам, хранящимся на диске. Информация разделяется на несколько страниц одинакового размера, которые хранятся последовательно друг за другом в пределах одного цилиндра (набора дорожек на дисках на одном расстоянии от центра), и каждая операция чтения или записи работает сразу с несколькими страницами. Для типичного диска размер страницы варьируется от до КБайт. После того, как головка установлена на нужную дорожку, а диск поворачивается так, что головка становится на начало интересующей нас страницы, чтение и запись становятся полностью электронными процессами, не зависящими от поворота диска, и диск может быстро читать или писать крупные объёмы данных.

В типичном приложении с B-деревом, объём хранимой информации так велик, что вся она просто не может храниться в основной памяти единовременно. Алгоритмы B-дерева копируют выбранные страницы с диска в основную память по мере надобности и записывает обратно на диск страницы, которые были изменены. Алгоритмы B-дерева хранят лишь определённое количество страниц в основной памяти в любой момент времени; таким образом, объём основной памяти не ограничивает размер B-деревьев, которые можно создавать.

Система в состоянии поддерживать в процессе работы в оперативной памяти только ограниченное количество страниц. Мы будем считать, что страницы, которые более не используются, удаляются из оперативной памяти системой; наши алгоритмы работы с В-деревьями не будут заниматься этим самостоятельно. Поскольку в большинстве систем время выполнения алгоритма, работающего с В-деревьями, зависит в первую очередь от количества выполняемых операций чтения/записи с диском, желательно минимизировать их количество и за один раз считывать и записывать как можно больше информации. Таким образом, размер узла В-дерева обычно соответствует дисковой странице. Количество потомков узла В-дерева, таким образом, ограничивается размером дисковой страницы.
Для больших В-деревьев, хранящихся на диске, степень ветвления обычно находится между и , в зависимости от размера ключа относительно размера страницы. Большая степень ветвления резко снижает как высоту дерева, так и количество обращений к диску для поиска ключа. Например, если есть миллиард ключей, и , то поиск ключа займёт две дисковые операции.

Перечисление

Деревья с метками

Формула Кэли утверждает, что там — это n деревьев на n помеченных вершинах. Классическое доказательство использует последовательности Прюфера, которые, естественно, показывают более сильный результат: количество деревьев с вершинами 1, 2,…, n степеней d 1, d 2,…, d n соответственно, является полиномиальным коэффициентом

(n — 2 d 1 — 1, d 2 — 1,…, dn — 1). {\ displaystyle {n-2 \ choose d_ {1} -1, d_ {2} -1, \ ldots, d_ {n} -1}.}

Более общая проблема состоит в подсчете остовных деревьев в неориентированном графе, к которому обращается теорема о матричном дереве. (Формула Кэли является частным случаем остовных деревьев в полном графе.) Аналогичная проблема подсчета всех поддеревьев независимо от размера: # P-complete в общем случае (Джеррам (1994)).

Деревья без меток

Подсчитать количество свободных деревьев без меток — более сложная задача. Замкнутая формула для числа t (n) деревьев с n вершинами от до изоморфизма графов неизвестна. Первые несколько значений t (n):

1, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159,… (последовательность A000055 в OEIS ).

Otter (1948) доказал асимптотическую оценку

t (n) ∼ C α nn — 5/2 при n → ∞, {\ displaystyle t (n) \ sim C \ alpha ^ {n} n ^ {- 5/2} \ quad {\ text {as}} n \ to \ infty,}

со значениями C и α, примерно равными 0,534949606… и 2.95576528565… (последовательность A051491 в OEIS ), соответственно (здесь f ~ g означает, что lim n → ∞ f / g = 1.) Это является следствием его асимптотической оценки числа r (n) немаркированных корневых деревьев с n вершинами:

r (n) ∼ D α nn — 3/2 при n → ∞, {\ displaystyle r ( n) \ sim D \ alpha ^ {n} n ^ {- 3/2} \ quad {\ text {as}} n \ to \ infty,}

с D около 0,43992401257… и тем же α, что и выше (см. Knuth (1997), глава 2.3.4.4 и Flajolet Sedgewick (2009), глава VII.5, стр. 475).

Первые несколько значений r (n):

1, 1, 2, 4, 9, 20, 48, 115, 286, 71 9, 1842, 4766, 12486, 32973,… (последовательность A000081 в OEIS )

Презентация на тему: » Дерево это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами.» — Транскрипт:

Дерево это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершинами имеется только по одному пути. Ориентированное (направленное) дерево -ориентированный граф, не содержащий циклов)

Дерево не имеет кратных рёбер и петель. Любое дерево с вершинами содержит ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда, где число вершин, число рёбер графа. Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственным элементарным путём. Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами. Для любых трёх вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.

Двоичное дерево древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Для практических целей обычно используют два подвида бинарных деревьев двоичное дерево поиска и двоичная куча. Общее применение управление иерархией данных; упрощение поиска информации (см. обход дерева); управление сортированными списками данных; синтактический разбор арифметических выражений, оптимизация программ; в качестве технологии компоновки цифровых картинок для получения различных визуальных эффектов; форма принятия многоэтапного решения

Двоичное дерево поиска это двоичное дерево, для которого выполняются следующие дополнительные условия Свойства дерева поиска : Оба поддерева левое и правое, являются двоичными деревьями поиска. У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X. В то время, как у всех узлов правого поддерева того же узла X значения ключей данных не меньше, нежели значение ключа данных узла X. Для различных операций двоичное дерево поиска можно определить так: Двоичное дерево состоит из узлов (вершин) записей вида (data, left, right), где data некоторые данные привязанные к узлу, left и right ссылки на узлы, являющиеся детьми данного узла — левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также определения поля parent в каждом узле (кроме корневого) — ссылки на родительский элемент. Данные (data) обладают ключом (key), на котором определена операция сравнения «меньше». В конкретных реализациях это может быть пара (key, value) — (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неё. Для любого узла X выполняются свойства дерева поиска: key]

Есть три способа обхода: Прямой Поперечный Обратный

Префиксный (прямой) обход сначала обрабатывается текущий узел, затем левое и правое поддеревья; Префиксный обход: A, B, D, H, E, C, F, I, J, G

Инфиксный (симметричный) обход сначала обрабатывается левое поддерево текущего узла, затем корень, затем правое поддерево; инфиксный обход: D, H, B, E, A, I, F, J, C, G

Постфиксный (обратный) обход сначала обрабатываются левое и правое поддеревья текущего узла, затем сам узел. постфиксный обход: H, D, E, B, I, J, F, G, C, A

1. Двоичная куча, пирамида, или сортирующее дерево такое двоичное дерево, для которого выполнены три условия: 2. Значение в любой вершине не меньше, чем значения её потомков. 3. Глубина листьев (расстояние до корня) отличается не более чем на 1 слой. 4. Последний слой заполняется слева направо. 5. Также двоичная куча просто реализуемая структура данных, позволяющая быстро (за логарифмическое время) добавлять элементы и извлекать элемент с максимальным приоритетом (например, максимальный по значению).

class Heap { int[] data; // массив с элементами (индексация с 1, 0 — фиктивная вершина) int pnt = 0; // указаетель на последний элемент /* Конструктор */ Heap(int size) { data = new int ; } /* Добавить элемент */ void add(int x) { data = x; for (int v = pnt, p = v >> 1; p > 0 && data > data; swap(data, p, v), v = p, p >>= 1); } /* Извлечь минимум */ int extractMin() { int ret = data; swap(data, 1, pnt—); for (int v = 1; (v

Примечания

, п. 171.
, п. 172.
^ Видеть .
^ , п. 206.
^ Видеть .
^ Видеть .
^ Видеть .
Стэнли Гилл Уильямсон (1985). Комбинаторика для компьютерных наук. Courier Dover Publications. п. 288. ISBN 978-0-486-42076-9.
Мехран Месбахи; Магнус Эгерштедт (2010). Теоретико-графические методы в многоагентных сетях. Издательство Принстонского университета. п. 38. ISBN 978-1-4008-3535-5.
Дин-Чжу Ду; Кер-И Ко; Сяодун Ху (2011). Разработка и анализ алгоритмов аппроксимации. Springer Science & Business Media. п. 108. ISBN 978-1-4614-1701-9.
^ , п. 207.
Джонатан Л. Гросс; Джей Йеллен; Пинг Чжан (2013). Справочник по теории графов, второе издание. CRC Press. п. 116. ISBN 978-1-4398-8018-0.
Бернхард Корте; Йенс Выген (2012). Комбинаторная оптимизация: теория и алгоритмы (5-е изд.). Springer Science & Business Media. п. 28. ISBN 978-3-642-24488-9.
Дэвид Макинсон (2012). Наборы, логика и математика для вычислений. Springer Science & Business Media. С. 167–168. ISBN 978-1-4471-2499-3.
Кеннет Розен (2011). Дискретная математика и ее приложения, 7-е издание. McGraw-Hill Science. п. 747. ISBN 978-0-07-338309-5.
Александр Шрайвер (2003). Комбинаторная оптимизация: многогранники и эффективность. Springer. п. 34. ISBN 3-540-44389-4.
, п. 150.
^ , п. 173.
Видеть
Видеть .