Сколько десятизначных чисел можно составить из 10 цифр

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

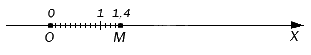
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Как здания строят из кирпичей, а слова складывают из букв, так натуральные числа записывают с помощью специальных знаков, которые называют цифрами . Этих цифр десять:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .

Натуральные числа, записанные одной цифрой, называют однозначными, двумя цифрами − двузначными , тремя цифрами − трехзначными и т.д. Все числа, кроме однозначных, называют многозначными. Многозначное число может начинаться с любой цифры, кроме цифр 0 .

Легко прочитать трехзначное число 917, однако число 17025543607 прочитать намного сложнее. Чтобы прочитать многозначное число, цифры его записи разбивают справа налево на группы по три цифры: 17 025 543 607 (при этом крайняя слева группа может состоять из трех цифр, из двух, как в данном примере, или из одной цифры). Эти группы называют классами . Первый справа класс называют классом единиц , второй справа − классом тысяч , третий − классом миллионов , четвертый − классом миллиардов и т.д.

При чтении многозначного числа число, записанное в каждом классе, читают как трехзначное, двузначное или однозначное, добавляя при этом название класса (как правило, название класса единиц не произносят). Число 17 025 543 607 читают: » 17 миллиардов 25 миллионов 543 тысячи 607 «.

Каждый класс разбивается справа налево на три разряда : единицы, десятки, сотни.

Так в приведенном примере в классе единиц 7 единиц, 0 десятков, 6 сотен, а в классе миллионов − 5 единиц, 2 десятка, 0 сотен. Названия всех разрядов числа 17 025 543 607 приведены в следующей таблице.

Запись натуральных чисел, который мы пользуемся, называют десятичной . Такое название связано с тем, что десять единиц каждого разряда составляют одну единицу следующего разряда, старшего разряда. Например, десять единиц составляют один десяток, десять десятков − одну сотню и т.д.

Число 2 958 можно представить в виде суммы:

2 958 = 2 000 + 900 + 50 + 8

2 958 = 2 * 1 000 + 9 * 100 + 5 * 10 + 8 * 1 .

Последнее равенство называют записью числа 2 958 в виде суммы разрядных слагаемых.

Общая стратегия решения

Для решения задачи, в которой Катя записала десятизначное число с различными цифрами, можно использовать следующую стратегию:

1. Анализ задачи. Внимательно прочитайте условие задачи и убедитесь, что правильно понимаете, что она требует от вас.

2. Понимание числа

Изучите записанное число Катей и обратите внимание на его особенности. В данной задаче цифры числа должны быть различными

3. Поиск возможных вариантов решения. Рассмотрите различные способы решения задачи. В данной задаче можно использовать перебор чисел, а также использовать математические операции и свойства чисел.

4. Выбор наиболее эффективного способа. Оцените время и усилия, которые требуются для каждого варианта решения, и выберите наиболее эффективный способ решения задачи.

5. Решение задачи и проверка. Примените выбранный способ решения задачи и получите результат. Проверьте правильность решения, сравнив его с условием задачи.

Следуя данной общей стратегии решения, вы сможете разгадать задачу, в которой Катя записала десятизначное число с различными цифрами.

Анализ доступных цифр

Десятизначное число представляет собой число, состоящее из десяти различных цифр. Такая задача задается Катей. Чтобы разгадать эту задачу, необходимо проанализировать доступные цифры.

Построение числа методами комбинаторики

Для разгадки задачи, которую записала Катя, о десятизначном числе с различными цифрами, можно использовать комбинаторику.

Комбинаторика — это раздел математики, который изучает способы комбинирования исходных элементов для получения новых комбинаций.

В данном случае нам нужно построить число из десяти различных цифр. Это означает, что каждая цифра должна быть выбрана из десяти возможных (от 0 до 9), и каждая цифра должна быть уникальной.

Для этого можно использовать принципы перестановок и сочетаний.

Перестановка — это упорядоченная выборка элементов из заданного множества. В нашем случае это десять цифр, которые Катя записала. Чтобы построить число с различными цифрами, необходимо выбрать первую цифру из десяти возможных, вторую — из оставшихся девяти, третью — из оставшихся восемь, и т.д. Таким образом, существует 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 10! (факториал) возможных перестановок.

Сочетание — это неупорядоченная выборка элементов из заданного множества. В нашем случае это также десять цифр, которые Катя записала. Так как порядок не имеет значения, нам не нужно учитывать все возможные перестановки. Количество сочетаний можно вычислить с помощью формулы сочетаний: С(n, k) = n! / (k! * (n-k)!) , где n — количество элементов, а k — количество выбранных элементов. В нашем случае, чтобы построить число с различными цифрами, нам нужно выбрать 10 цифр из десяти возможных, то есть С(10, 10) = 10! / (10! * (10-10)!) = 1.

Таким образом, существует только одно число, которое можно построить методами комбинаторики из десяти различных цифр, записанных Катей.

Различные способы проверки верности результата

Математический метод:

Для определения количества десятизначных чисел, которые можно составить из 10 цифр, необходимо использовать принцип комбинаторики. Для первой позиции числа можно выбрать любую из 10 цифр (от 0 до 9), для второй позиции — любую из оставшихся 9 цифр и так далее. Поэтому общее количество десятизначных чисел можно вычислить как произведение количества доступных цифр на каждой позиции.

Таким образом, общее количество десятизначных чисел равно 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3 628 800.

Важно учитывать, что это количество включает все десятизначные числа, включая ведущие нули (например, 0000000001). Проверка с помощью программного кода:

Проверка с помощью программного кода:

Другим способом проверки верности результата является написание программного кода для подсчета всех возможных десятизначных чисел из 10 цифр. Например, можно написать программу на языке программирования Python, которая будет генерировать все возможные комбинации цифр и считать их количество.

Вот пример программного кода на языке Python:

Запустив эту программу, мы получим результат, который должен быть равен 3 628 800. Если программа выведет другое значение, значит, что-то не так.

Итак, мы рассмотрели задачу о составлении десятизначных чисел из 10 цифр. При решении этой задачи мы использовали принципы комбинаторики и перестановок. В результате мы узнали, что количество десятизначных чисел, которые можно составить из 10 цифр, составляет:

• 9 вариантов для первой цифры числа, так как ноль не может стоять на первом месте;
• 10 вариантов для второй цифры;
• 10 вариантов для третьей цифры;
• …
• 10 вариантов для десятой цифры.

Итого, общее количество десятизначных чисел равно произведению количества вариантов для каждой цифры:

9 * 10 * 10 * 10 * 10 * 10 * 10 * 10 * 10 * 10 = 90 000 000 000.

Таким образом, можно составить 90 000 000 000 десятизначных чисел из 10 цифр.

Арифметическая последовательность чисел

Арифметическая последовательность чисел представляет собой последовательность, в которой каждый следующий элемент получается прибавлением к предыдущему элементу одного и того же числа, называемого разностью. Как найти наименьшее десятизначное число в такой последовательности?

Для этого необходимо определить разность арифметической последовательности, а затем последовательно прибавлять ее к начальному числу до тех пор, пока полученное число не будет иметь десять знаков.

Например, если разность равна 1, то наименьшее десятизначное число можно получить, начиная с числа 1 и последовательно прибавляя 1, пока не получится число с десятью знаками. В этом случае наименьшее десятизначное число будет равно 10,000,000,001.

Если разность равна -1, то наименьшее десятизначное число можно получить, начиная с числа 9 и последовательно прибавляя -1, пока не получится число с десятью знаками. В этом случае наименьшее десятизначное число будет равно 9,999,999,999.

Таким образом, чтобы найти наименьшее десятизначное число в арифметической последовательности, необходимо знать разность и выполнять последовательные прибавления или вычитания до получения числа с десятью знаками.

Понятие арифметической прогрессии

Арифметическая прогрессия это последовательность чисел, в которой каждое следующее число получается путем прибавления к предыдущему числу одного и того же фиксированного числа, называемого разностью.

Десятизначное число — это число, которое содержит 10 цифр. Для записи наименьшего десятизначного числа, в котором разность между соседними числами будет равна, например, 5, нужно взять число 10^9 и прибавить к нему 5, затем прибавить 5 к результату и так далее, пока не получится число с 10 цифрами.

Как записать наименьшее десятизначное число с разностью 5 в арифметической прогрессии? Одним из способов будет следующий:

1. Начинаем с числа 10^9 = 1000000000
2. Прибавляем к нему разность 5 и получаем 1000000005
3. Прибавляем еще разность 5 и получаем 1000000010
4. Продолжаем такое действие еще 6 раз, получаем 1000000035

Примеры арифметических последовательностей

Арифметическая последовательность — это последовательность чисел, в которой каждый следующий член получается прибавлением одного и того же числа к предыдущему. Такие последовательности можно использовать в различных математических моделях и задачах.

Как записать наименьшее десятизначное число, используя арифметическую последовательность? Для этого можно воспользоваться формулой арифметической прогрессии:

an = a1 + (n-1)d,

где an — n-й член последовательности, a1 — первый член последовательности, d — разность между соседними членами.

Чтобы получить наименьшее десятизначное число, можно выбрать a1 = 1 и d = 1. Тогда можно записать последовательность чисел следующим образом:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10

Таким образом, наименьшее десятизначное число можно записать с помощью арифметической последовательности, начинающейся с числа 1 и имеющей разность 1.

Первая цифра десятизначного числа

Для определения значения десятизначного числа необходимо обратить внимание на его первую цифру. Первая цифра обозначает разрядность числа, а также позволяет понять его порядок величины

Следующие пункты помогут разобраться с первой цифрой десятизначного числа:

1. 0: Если первая цифра равна нулю, то это означает, что число начинается с нуля и имеет более одной цифры. Например, число 0123456789 начинается с нуля, но не считается десятизначным числом, так как ноль в начале числа не имеет значения.
2. 1-9: Если первая цифра десятизначного числа от 1 до 9, то она указывает на разрядность числа. Например, если первая цифра равна 1, то число находится в диапазоне от 1000000000 до 1999999999. Аналогично, если первая цифра равна 9, то число находится в диапазоне от 9000000000 до 9999999999.

Первая цифра десятизначного числа играет важную роль при его интерпретации и позволяет сразу понять примерный порядок величины числа. Это помогает лучше понять его значимость и оценить его относительность в рамках других чисел.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , ( 4 ) , а 76 , 134134134134 … – как 76 , ( 134 ) .

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 ( 7 ) и 0 , 6 ( 77 ) и т.д. Также допустимы записи вида 0 , 67777 ( 7 ) , 0 , 67 ( 7777 ) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0 , 6 ( 7 ) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 ( 34 ) .

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 ( 0 ) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 ( 9 ) , 31 , 6 ( 9 ) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают ( 0 ) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8 , 31 ( 9 ) можно заменить на соответствующую ей дробь 8 , 32 ( 0 ) . Или 4 , ( 9 ) = 5 , ( 0 ) = 5 .

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Значимость количества цифр в десятизначном числе

Десятизначные числа играют важную роль в математике и повседневной жизни. Количество цифр в десятизначном числе определяет его значимость и может влиять на многие аспекты, такие как точность, представление данных и понимание числовых концепций. В данной статье мы рассмотрим несколько аспектов значимости количества цифр в десятизначном числе.

Точность и представление чисел

Десятизначное число имеет 10 цифр, от 0 до 9. Чем больше цифр, тем больше чисел можно представить. Например, десятизначное число может быть 1000000000 (1 с 9 нулями) или 999999999 (9 девяток). Каждая цифра в числе имеет определенную позицию, которая определяет ее вес, и влияет на общую величину числа.

Операции с десятизначными числами

Количество цифр в десятизначном числе влияет на результаты математических операций. Например, при сложении двух десятизначных чисел сумма может превысить или быть меньше десятизначного числа, в зависимости от цифр и их весов. Аналогично, при умножении или делении десятизначных чисел, количество цифр может влиять на точность и представление результата.

Числа и информация

В повседневной жизни десятизначные числа часто используются для представления информации, такой как номера телефонов, даты, коды и т. д. Количество цифр в числе может быть ограничено требованиями и нормами. Например, номер телефона может быть задан фиксированным количеством цифр для облегчения идентификации и набора.

Заключение

Таким образом, количество цифр в десятизначном числе имеет значимость в математике, точности операций и представлении информации. В зависимости от контекста использования, количество цифр может ограничиваться и влиять на различные аспекты числовых концепций.

Определение [ править | править код ]

Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.

Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:

x = ± ∑ k = 0 n − 1 a k 10 k <displaystyle x=pm sum _^a_10^> , где a k <displaystyle a_> — это целые числа, называемые цифрами, удовлетворяющие неравенству 0 ≤ a k ≤ 9. <displaystyle 0leq a_leq 9.>

Обычно для ненулевого числа x требуют, чтобы старшая цифра a n − 1 <displaystyle a_> в десятичном представлении x была также ненулевой.

Например, число сто три представляется в десятичной системе счисления в виде:

103 = 1 ⋅ 10 2 + 0 ⋅ 10 1 + 3 ⋅ 10 0 . <displaystyle 103=1cdot 10^<2>+0cdot 10^<1>+3cdot 10^<0>.>

С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до 10 n − 1 <displaystyle 10^-1> , то есть, всего 10 n <displaystyle 10^> различных чисел.

Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:

a n − 1 a n − 2 … a 1 a 0 , a − 1 a − 2 … a − ( m − 1 ) a − m = ∑ k = − m n − 1 a k 10 k , <displaystyle a_a_dots a_<1>a_<0>,a_<-1>a_<-2>dots a_<-(m-1)>a_<-m>=sum _^a_10^,>

где n — число разрядов целой части числа, m — число разрядов дробной части числа.

Двоично-десятичное кодирование

В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр, при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Двоично-десятичные числа требуют большего количества битов для своего хранения . Так, четыре двоичных разряда имеют 16 состояний, и при двоично-десятичном кодировании 6 из 16 состояний двоичной тетрады не используются .

Таблица сложения в десятичной системе счисления

+		1	2	3	4	5	6	7	8	9	10
		1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10	11
2	2	3	4	5	6	7	8	9	10	11	12
3	3	4	5	6	7	8	9	10	11	12	13
4	4	5	6	7	8	9	10	11	12	13	14
5	5	6	7	8	9	10	11	12	13	14	15
6	6	7	8	9	10	11	12	13	14	15	16
7	7	8	9	10	11	12	13	14	15	16	17
8	8	9	10	11	12	13	14	15	16	17	18
9	9	10	11	12	13	14	15	16	17	18	19
10	10	11	12	13	14	15	16	17	18	19	20

Таблица умножения в десятичной системе

×		1	2	3	4	5	6	7	8	9	10
1		1	2	3	4	5	6	7	8	9	10
2		2	4	6	8	10	12	14	16	18	20
3		3	6	9	12	15	18	21	24	27	30
4		4	8	12	16	20	24	28	32	36	40
5		5	10	15	20	25	30	35	40	45	50
6		6	12	18	24	30	36	42	48	54	60
7		7	14	21	28	35	42	49	56	63	70
8		8	16	24	32	40	48	56	64	72	80
9		9	18	27	36	45	54	63	72	81	90
10		10	20	30	40	50	60	70	80	90	100

Примеры решения

Пример 1:

Пример 2:

Пример 3:

Предположим, что Катя записала число 1122334455. В этом случае мы видим, что некоторые цифры повторяются. Поэтому мы не можем быть уверены, что это число, которое Катя записала.

Таким образом, чтобы разгадать задачу Кати, необходимо проверить, все ли цифры в числе различны. Если да, то это и есть число, которое Катя записала. Если нет, то мы не можем быть уверены в правильном ответе.

Пример с перебором вариантов

Катя записала десятизначное число, в котором все цифры различны. Теперь она задает тебе вопрос: «Можешь ли ты разгадать это число?». Представь себе задачку, в которой нужно перебрать все возможные варианты чисел с разными цифрами.

Для решения этой задачи можно использовать циклы и условные операторы. Например, можешь начать с цифры 1 и проверить, можно ли собрать десятизначное число, используя только разные цифры. Если это не получается, то переходи к следующей цифре и так далее, пока не найдешь число, удовлетворяющее условиям задачи.

Например, представим, что Катя записала число, где первая цифра 1, вторая цифра 2, третья цифра 3 и так далее до 9. То есть число будет выглядеть следующим образом: 123456789. Такое число удовлетворяет условиям задачи, так как все цифры различны и число имеет десять цифр.

Таким образом, пример с перебором вариантов позволяет найти число, удовлетворяющее условиям задачи Кати. Однако, следует учитывать, что такой подход может быть достаточно времязатратным, особенно при большом количестве цифр.

Пример с математическим анализом

Предположим, что Катя записала десятизначное число, в котором все цифры различны. Давайте проанализируем, что можно сказать о таком числе в математическом плане.

Первое, что стоит отметить, это то, что десятизначное число обязательно содержит все цифры от 0 до 9. Таким образом, можно утверждать, что Катя записала число, в котором используются все цифры от 0 до 9 и ни одна цифра не повторяется.

Также стоит отметить, что в десятизначном числе порядок цифр имеет значение. Это значит, что если переставить цифры местами, то получится совершенно другое число. Если Катя записала число, причем все цифры различны, то каждая цифра занимает свое место в числе и изменение порядка цифр приведет к совершенно другому значению.

Иными словами, если Катя переставит цифры числа, она получит новое число, которое будет отличаться от исходного числа. Это свойство можно использовать для нахождения различных перестановок и анализа чисел, получаемых при перестановке цифр.