Что означает значение дроби равное нулю?

Смысл и значение дробей

Одним из основных смыслов дробей является представление части от целого. Например, если имеется пирог, который разделен на 4 равные части, то каждая часть может быть представлена в виде дроби: 1/4 пирога. Дроби помогают нам разделить целое на равные части и указать, сколько частей мы имеем или используем.

Дроби также используются для представления числителей и знаменателей в различных физических и математических контекстах. Например, в физике дроби могут представлять отношение массы к объему, плотность или скорость. В математике дроби широко используются для представления десятичных дробей, долей и процентов.

Однако, следует помнить, что дробь равна нулю тогда и только тогда, когда ее числитель обращается в ноль. Это математическое свойство позволяет нам определить особые значения и свойства дробей и использовать их в решении математических задач и уравнений.

Таким образом, понимание смысла и значения дробей является необходимым навыком для успешного применения и использования их в реальных ситуациях. Независимо от того, используем ли мы их для вычислений, измерений или анализа данных, дроби остаются важным инструментом, который помогает нам лучше понять и описать мир вокруг нас.

Как решать неопределенные дроби

Для решения неопределенных дробей необходимо следовать определенным шагам:

Шаг 1: Найдите неопределенную дробь в задаче. Обычно она выглядит в виде 0/0 или ∞/∞.

Шаг 2: Преобразуйте неопределенную дробь, чтобы ее можно было решить. Один из способов — использование арифметических операций для сокращения дробей или замены переменных.

Шаг 3: Примените правила арифметики и алгебры для решения получившейся неопределенной дроби. Это может включать упрощение, раскрытие скобок, факторизацию и другие операции.

Шаг 4: Используйте предельные значения, чтобы найти конечный результат. Если неопределенная дробь относится к определенной функции или графику, подставьте пределы вместо переменных и рассчитайте результат.

Шаг 5: Проверьте ответ с помощью математических вычислений или графиков, если это возможно. Убедитесь, что ваш ответ правильный и соответствует задаче.

Решение неопределенных дробей может быть сложным, но правильное применение арифметических и алгебраических операций позволяет найти корректный результат.

Деление на ноль и области определения

При делении числа на ноль, получается результат, который не имеет смысла и не определен. Такую ситуацию называют «делением на ноль». Математические операции над числами предполагают определенные правила и законы, которые делают их область определения конечной и понятной.

Область определения описывает множество значений, для которых функция (в данном случае деление) имеет смысл и является определенной. Деление на ноль не имеет области определения, так как результат не может быть определен в математическом смысле.

Деление на ноль может привести к различным противоречивым и нелогичным результатам. Например, возникает противоречие при вычислении таких выражений, как 1/0 или 0/0. В целом, данная ситуация не имеет решения и не может быть представлена в виде десятичной дроби или дроби в общем виде.

Поэтому, в математике и в программировании существуют правила, которые запрещают деление на ноль. Это сделано для обеспечения корректного и понятного результата вычислений.

Важно помнить, что при программировании и использовании математических выражений, необходимо проверять область определения функции и избегать деления на ноль. В противном случае, может возникнуть ошибка или некорректный результат, который будет трудно отследить и исправить

Таким образом, деление на ноль не имеет области определения и не имеет смысла в математике. Правила и законы математических операций предполагают определенность и понятность результатов, поэтому деление на ноль запрещено и следует избегать.

Обоснование метода

В основе доказательства утверждения из предыдущего пункта лежит хорошо известный факт: дробь a/b , b≠0 равна нулю тогда и только тогда, когда ее числитель есть нуль. Этот факт вытекает из определения дроби (дробь a/b , b≠0 есть такое число c , что b·c=a ) и из того, что произведение двух чисел тогда и только тогда равно нулю, когда одно из чисел есть нуль.

Начнем с доказательства частных случаев.

Докажем, что решение уравнения 0/g(x)=0 есть ОДЗ для него. В силу того, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, равенство 0/g(x)=0 является верным для любого числа x , при котором оно имеет смысл. Очевидно, что равенство 0/g(x)=0 имеет смысл тогда и только тогда, когда x принадлежит ОДЗ для уравнения 0/g(x)=0 . Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.

Докажем, что уравнение C/g(x)=0 , где С – отличное от нуля число, не имеет решений. Так как дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, то равенство C/g(x)=0 , C≠0 не может быть верным ни для какого числа x . Следовательно, уравнение C/g(x)=0 , C≠0 не имеет решений.

Теперь будем считать, что числитель дроби f(x)/g(x) есть выражение с переменной, а не число, и докажем, что множество решений уравнения f(x)/g(x)=0 совпадает с множеством решений уравнения f(x)=0 на ОДЗ для уравнения f(x)/g(x)=0 . Для этого достаточно доказать два момента: первый — что любой корень уравнения f(x)/g(x)=0 является корнем уравнения f(x)=0 , второй — что любой корень уравнения f(x)=0 , принадлежащий ОДЗ для уравнения f(x)/g(x)=0 , является корнем уравнения f(x)/g(x)=0 .

Приступаем к доказательству первой части. Пусть x – корень уравнения f(x)/g(x)=0 . Тогда f(x)/g(x)=0 – верное числовое равенство. Из этого неравенства и из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что f(x)=0 . А это равенство означает, что x – корень уравнения f(x)=0 .

Первая часть доказана. Приступаем к доказательству второй части.

Пусть x принадлежит ОДЗ для уравнения f(x)/g(x)=0 и при этом x — корень уравнения f(x)=0 . Так как x принадлежит ОДЗ для уравнения f(x)/g(x)=0 , то дробь f(x)/g(x) имеет смысл. Так как x – корень уравнения f(x)=0 , то f(x)=0 – верное числовое равенство. Из этих результатов, а также из того факта, что дробь равна нулю тогда и только тогда, когда ее числитель есть нуль, следует, что дробь f(x)/g(x) равна нулю, то есть, f(x)/g(x)=0 . А это равенство означает, что x – корень уравнения f(x)/g(x)=0 .

Так доказана вторая часть и все утверждение в целом.

Деление на ноль приводит к неопределенности

Когда деление на ноль осуществляется в математике, результат становится неопределенным. Это означает, что мы не можем однозначно определить значение данного выражения. Почему это происходит?

Прежде чем мы попытаемся разобраться, давайте вспомним основы математики. В математике существует правило, которое гласит: «Деление любого числа на ноль запрещено». И это не произвольное правило, а зависит от самой природы чисел и операций над ними.

Возьмем, к примеру, простую дробь 1/0. Попробуем разобраться, как бы мы могли определить ее значение. Если мы поделим 1 на очень маленькое число, то получим очень большое число. Но когда мы пытаемся приблизиться к делению на ноль, наш результат стремится к бесконечности. Однако, бесконечность — это не конкретное число, а скорее понятие, которое находится за рамками числовой оси.

Таким образом, когда мы пытаемся разделить число на ноль, мы не можем установить точное значение для этой операции. Просто потому, что деление на ноль остается вне сферы определенности в математике.

Деление на ноль приводит к неопределенности во многих областях. Например, в физике и инженерии, где числа являются инструментом для моделирования и предсказания различных явлений, деление на ноль может вызвать некорректные результаты и привести к ошибкам.

Также стоит упомянуть, что деление на ноль не имеет математического смысла. Если мы делим что-то на что-то другое, мы ожидаем получить результат. Но когда мы делаем это на ноль, мы сталкиваемся с противоречием в математических правилах и понятиях.

В целом, деление на ноль является интересным исследовательским вопросом для математиков. Чтобы понять, как обрабатывать такие операции и избежать неопределенностей, нужно строить математические модели и разрабатывать новые подходы для работы с делением на ноль.

Математические операции с неопределенными дробями

Сложение неопределенных дробей

При сложении неопределенных дробей с одинаковыми знаменателями, числители складываются:

a/b + c/b = (a + c)/b

Если числители имеют одинаковую структуру, можно сократить:

k(b + b) / b = 2kb / b = 2k

Если знаменатели разные, то сложение невозможно, так как значения знаменателей неизвестны.

Вычитание неопределенных дробей

При вычитании неопределенных дробей с одинаковыми знаменателями, числители вычитаются:

a/b — c/b = (a — c)/b

Если числители имеют одинаковую структуру, можно сократить:

k(b — b) / b = 0

Если знаменатели разные, то вычитание невозможно, так как значения знаменателей неизвестны.

Умножение неопределенных дробей

При умножении неопределенной дроби на число, значение числителя умножается на это число, знаменатель остается неизменным:

a/b * c = (a * c)/b

Умножение неопределенных дробей не имеет особенностей в зависимости от структуры числителей и знаменателей.

Деление неопределенных дробей

При делении неопределенной дроби на число, значение числителя делится на это число, знаменатель остается неизменным:

a/b / c = (a / c)/b

Также, можно сократить неопределенную дробь, если числитель и знаменатель имеют одинаковую структуру:

(kb)/(kb) = 1

Операции с неопределенными дробями требуют аккуратности и внимательности, чтобы избежать ошибок и получить верный результат.

Сложение и вычитание неопределенных дробей

Для сложения неопределенных дробей необходимо иметь общий знаменатель. Если знаменатели различаются, нужно привести их к общему знаменателю. Затем сложить числители и записать результат вместе с общим знаменателем.

Пример:

Неопределенная дробь	Сложение
2/x	+	3/x	=	2 + 3/x	=	5/x

Для вычитания неопределенных дробей также необходим общий знаменатель. Полученную разность числителей записывают вместе с общим знаменателем.

Пример:

Неопределенная дробь	Вычитание
5/x	—	3/x	=	5 — 3/x	=	2/x

Сложение и вычитание неопределенных дробей сводятся к простой алгебраической операции сложения или вычитания чисел в числителях, при условии совпадения знаменателей.

Важно помнить, что неопределенные дроби могут могут иметь различные условия на переменные (например, исключения на значения переменных), поэтому результаты сложения и вычитания не всегда будут иметь общий знаменатель

Умножение и деление неопределенных дробей

В случае умножения двух неопределенных дробей, необходимо умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби. Полученные числитель и знаменатель образуют новую неопределенную дробь.

Например, умножение неопределенной дроби x/_y на a/_b будет выглядеть следующим образом: x * a/_{y * b}.

При делении двух неопределенных дробей, необходимо умножить числитель первой дроби на знаменатель второй дроби и знаменатель первой дроби на числитель второй дроби. Результатом будет новая неопределенная дробь.

Например, деление неопределенной дроби x/_y на a/_b будет выглядеть следующим образом: x * b/_{y * a}.

Важно помнить, что неопределенные дроби сохраняют свои особенности при умножении и делении. Если у неопределенной дроби есть знаменатель равный нулю, то результат умножения или деления будет также неопределенной дробью с знаменателем равным нулю

Умножение и деление неопределенных дробей является важным элементом в решении математических задач и используется в различных сферах, таких как физика, экономика, и т.д.

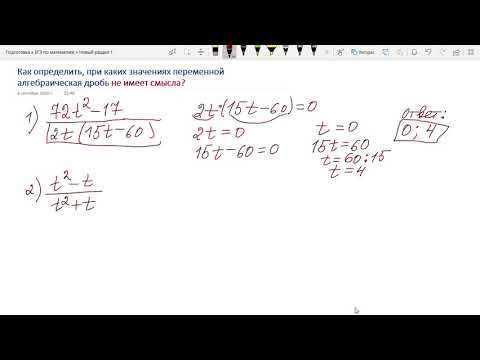
Видео:Как найти значения переменной, при которых алгебраическая дробь не имеет смысла?Скачать

Действия с нулем

Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов действий
:

• Сложение;
• Умножение;
• Вычитание;
• Деление (ноля на число);
• Возведение в степень.

Важно!
Если при сложении к любому числу прибавить ноль, то это число останется прежним и не поменяет своего числового значения. То же произойдет, если от любого числа отнять ноль

При умножении и делении все обстоит немного иначе. Если умножить любое число на ноль
, то и произведение тоже станет нулевым.

Рассмотрим пример:

Запишем это как сложение:

Всего складываемых нолей пять, вот и получается, что

Попробуем один умножить на ноль
. Результат также будет нулевым.

Ноль также можно разделить на любое другое число, не равное ему. В этом случае получится , значение которой также будет нулевым. Это же правило действует и для отрицательных чисел. Если ноль делить на отрицательное число, то получится ноль.

Также можно возвести любое число в нулевую степень
. В таком случае получится 1

При этом важно помнить, что выражение «ноль в нулевой степени» абсолютно бессмысленно. Если попытаться возвести ноль в любую степень, то получится ноль

Пример:

Пользуемся правилом умножения, получаем 0.

Так можно ли делить на ноль

Итак, вот мы и подошли к главному вопросу. Можно ли делить на ноль
вообще? И почему же нельзя разделить число на ноль при том, что все остальные действия с нулем вполне существуют и применяются? Для ответа на этот вопрос необходимо обратиться к высшей математике.

Начнем вообще с определения понятия, что же такое ноль? Школьные учителя утверждают, что ноль-это ничто. Пустота. То есть когда ты говоришь, что у тебя 0 ручек, это значит, что у тебя совсем нет ручек.

В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь ноль называют неопределенностью, так как если провести небольшое исследование, то получается, что при делении ноля на ноль мы можем в результате получить любое другое число, которое не обязательно может быть нолем.

Знаете ли вы, что те простые арифметические действия, которые вы изучали в школе не так равноправны между собой? Самыми базовыми действиями являются сложение и умножение
.

Для математиков не существует понятий « » и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:

Таким образом, получается, что неизвестной разностью является некое число, которое нужно прибавить к 3, чтобы получить 5. То есть, не нужно ничего вычитать, нужно просто найти подходящее число. Это правило действует для сложения.

Немного иначе дела обстоят с правилами умножения и деления.
Известно, что умножение на ноль приводит к нулевому результату. Например, если 3:0=х, тогда, если перевернуть запись, получится 3*х=0. А число, которое умножалось на 0 даст ноль и в произведении. Получается, что числа, которое бы давало в произведении с нолем какую-либо величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.

Но что будет, если попытаться разделить сам ноль на себя же? Возьмем как х некое неопределенное число. Получается уравнение 0*х=0. Его можно решить.

Если мы попробуем взять вместо х ноль, то мы получим 0:0=0. Казалось бы, логично? Но если мы попробуем вместо х взять любое другое число, например, 1, то в конечном итоге получится 0:0=1. Та же ситуация будет, если взять любое другое число и подставить его в уравнение
.

В этом случае получится, что мы можем как множитель взять любое другое число. Итогом будет бесконечное множество разных чисел. Порой все же деление на 0 в высшей математике имеет смысл, но тогда обычно появляется некое условие, благодаря которому мы сможем все-таки выбрать одно подходящее число. Это действие называется «раскрытием неопределенности». В обычной же арифметике деление на ноль снова потеряет свой смысл, так как мы не сможем выбрать из множества какое-то одно число.

Важно!
На ноль нельзя разделить ноль

Компьютерная арифметика

Большинство калькуляторов, таких как этот Инструменты Техаса ТИ-86, остановит выполнение и отобразит сообщение об ошибке, когда пользователь или запущенная программа попытается разделить на ноль.

Деление на ноль на Android 2.2.1 калькулятор показывает символ бесконечности.

В Стандарт IEEE с плавающей запятой, поддерживается практически всеми современными единицы с плавающей запятой, указывает, что каждый плавающая точка арифметическая операция, включая деление на ноль, дает четко определенный результат. Стандарт поддерживает подписанный ноль, а также бесконечность и NaN (не число). Есть два нуля: +0 (положительный ноль) и −0 (отрицательный ноль), и это устраняет любую двусмысленность при разделении. В IEEE 754 арифметика, а ÷ +0 положительная бесконечность, когда а положительная, отрицательная бесконечность, когда а отрицательно, и NaN, когда а = ± 0. Знаки бесконечности меняются при делении на −0 вместо.

Обоснованием этого определения является сохранение знака результата в случае арифметическое истощение. Например, при вычислении с одинарной точностью 1 / (Икс/ 2), где Икс = ±2−149, вычисление Икс/ 2 переполняется и дает ± 0 со знаком соответствия Икс, и результат будет ± ∞ с соответствием знаков Икс. Знак будет соответствовать точному результату ± 2150, но величина точного результата слишком велика для представления, поэтому бесконечность используется для обозначения переполнения.

Целочисленное деление на ноль обычно обрабатывается иначе, чем деление с плавающей запятой, поскольку для результата нет целочисленного представления. Некоторые процессоры генерируют исключение когда делается попытка разделить целое число на ноль, хотя другие просто продолжат и сгенерируют неверный результат для деления. Результат зависит от того, как реализовано деление, и может быть либо нулем, либо иногда максимально возможным целым числом.

Из-за неправильных алгебраических результатов приписывания любого значения делению на ноль многие компьютеры языки программирования (в том числе используемые калькуляторы ) явно запрещает выполнение операции и может преждевременно остановить программу, которая пытается ее выполнить, иногда сообщая об ошибке «Делить на ноль». В этих случаях, если требуется какое-то особое поведение для деления на ноль, условие должно быть явно проверено (например, с использованием если заявление ). Некоторые программы (особенно те, которые используют арифметика с фиксированной точкой там, где нет специального оборудования с плавающей запятой) будет использовать поведение, аналогичное стандарту IEEE, используя большие положительные и отрицательные числа для аппроксимации бесконечностей. В некоторых языках программирования попытка разделить на ноль приводит к неопределенное поведение. Графический язык программирования Scratch 2.0 и 3.0 Используемый во многих школах, возвращает Infinity или -Infinity в зависимости от знака дивиденда.

В два дополнения В арифметике попытки разделить наименьшее целое число со знаком на -1 сопровождаются аналогичными проблемами и обрабатываются с тем же диапазоном решений, от явных условий ошибки до неопределенное поведение.

Большинство калькуляторов либо возвращают ошибку, либо сообщают, что 1/0 не определено; однако некоторые TI и HP графические калькуляторы оценят (1/0)2 до ∞.

Microsoft Math и Mathematica вернуть за 1/0. Клен и SageMath возвращает сообщение об ошибке для 1/0 и бесконечность для 1 / 0,0 (0,0 указывает этим системам использовать арифметику с плавающей запятой вместо алгебраической арифметики).

Некоторые современные калькуляторы позволяют деление на ноль в особых случаях, когда это будет полезно студентам и, предположительно, будет понятно математикам в контексте. Некоторые калькуляторы, онлайн Desmos калькулятор является одним из примеров, разрешить арктангенс (1/0). Студентов часто учат, что функция обратного котангенса арккотангенс, следует вычислить, взяв арктангенс обратной величины, поэтому калькулятор может разрешить арктангенс (1/0), давая результат π2{ displaystyle { tfrac { pi} {2}}}, который является правильным значением арккотангенса 0. Математическое обоснование состоит в том, что предел, когда x стремится к нулю арктангенса 1 / x, равен π2{ displaystyle { tfrac { pi} {2}}}.

2.5 Что такое ноль?

1. Потребность в нуле появилась при определении операции вычитания.
2. Для разрешения большей части неопределенностей вычитания было введено “правило перестановки”. Знак минус перед числом, по сути, является маркером “отложенного вычитания”. Все что “правило перестановки” не осилило, закрыл собой ноль. По сути, ноль был введен для обозначения понятия “ничто”.
   В предыдущей части статьи (при проективном расширении числовой прямой) мы “с потолка” ввели беззнаковую бесконечность. Ноль, аналогичная “затычка” для всего, что нам не понятно. Последствия, в виде появления новых неопределенностей, оказываются весьма предсказуемы.
3. У понятия “ничто”, отсутствует связь с понятием “количество” (основа для определения натуральных чисел и сложения). Эти понятия существуют сами по себе и мы можем “созерцать” их совершенно независимо, например “пять яблок” и “вакуум”. Отсюда следует, что в своей сути ноль так же не связан с натуральными числами, как понятие “ничто” не связанно с понятием “количество”.

Вычитание использует данное понятие, но не порождает его.Отсутствие породившей операции качественно отличает ноль от всех остальных чисел.

Для того, чтобы была ясна связь не рассмотренных нами типов чисел с операциями, продолжим, максимально кратко, тему эволюции. Мы остановились на делении. Комплексные числа и часть иррациональных порождаются операцией взятия корня (логарифмированием) над отрицательным числом. Прочие иррациональные (число Пи и число Эйлера) появляются за счет введения бесконечных сумм и бесконечных умножений. Мнимые единицы кватернионов даны по определению и не выведены арифметически. Соответственно, инородны в рамках эволюции чисел.
4. Вероятно именно из-за возможности одновременного “созерцания” понятия “ничто” и понятия “количество” к натуральным числам. Однако гораздо более логичным видится вынесение нуля как минимум в отдельный тип чисел.
5. Было принято, что ноль единый и абсолютный. Именно из этого, весьма спорного, предположения следуют “правила сложения/вычитания нуля” с другими числами. Как следствие, ноль обладает уникальным свойством, которое отсутствует у всех остальных чисел. В результате сложения нуля с произвольным числом неизвестно, сколько нулей участвовало в операции и были ли они вообще.

невозможно дать ответМатематическим языком:


колесах“знаковым нулем”Математическим языком:

Целые рациональные уравнения

Если в уравнении нет переменной \(x\) в знаменателе, то такое уравнение называется целым. Или, другими словами, нигде в уравнении нет деления на переменную.
Метод решения целых рациональных уравнений сильно зависит от того, какой степени перед вами уравнения.

Степень уравнения — это максимальная степень у переменной \(x\).

Например, уравнение \(x^2+5x-1=0\) будет второй степени, так как есть \(x^2\).
Пример уравнения первой степени: \(5x-1=17\);
Уравнение третьей степени: \(5x^3-3x^2=0\);
Уравнение четвертой степени: \(7x^4-5x^2+x-5=0\);
И т.д.

Основной алгоритм решения целых уравнений:

• Если есть скобки, раскрываем их;
• Перекидываем все слагаемые в левую часть так, чтобы в правой части остался только \(0\). Не забываем при этом менять знак этих слагаемых;
• Приводим подобные слагаемые;
• Если получилось уравнение первой степени (в уравнении есть только \(x\)), то решаем его так (линейные уравнения);
• Если получилось уравнение второй степени (в уравнении есть \(x^2\)), то оно решается вот так (квадратные уравнения).
• А вот если в преобразованном уравнении получились члены \(x^3\) или большей степени, то придется применять нестандартные методы решения. Например, замена переменной, группировка, схема Горнера и т.д.

Чаще всего уравнения после преобразований будут сводиться к уравнениям первой (линейные уравнения) и второй (квадратные уравнения) степени.

Разберем примеры целых рациональных уравнений:

Пример 1
$$-4(-7+6x)=-9x-5;$$
Первым делом раскрываем скобки:
$$28-24x=-9x-5;$$
Перекидываем все слагаемые из правой части в левую:
$$28-24x+9x+5=0;$$
Поменяем слагаемые местами, чтобы удобнее было приводить подобные слагаемые:
$$-24x+9x+5+28=0;$$
$$-15x+33=0;$$
Получили линейное уравнение. Чтобы его решить, перекидываем свободный член (тот, что без \(x\)) в правую часть:
$$-15x=-33;$$
И поделим уравнение слева и справа на \(-15\):
$$x=\frac{-33}{-15};$$
$$x=\frac{11}{5}=2,2;$$
Ответ: \(x=2,2.\)

Важно отметить, то, что уравнение линейное, стало видно сразу после раскрытия скобок: у нас же не было степени у \(x\)-ов. Поэтому разумно было сразу решать его как линейное: перенести все слагаемые с \(x\) в левую часть, а все числа в правую

Так бы получилось немного короче.

Пример 2
$$4*(x+1)^2-2(x+3)=(2x-5)^2;$$
Тут сразу и не скажешь, какой степени уравнение. На первый взгляд кажется, что квадратное, но давайте раскроем скобки, воспользовавшись формулами сокращенного умножения:
$$4*(x^2+2x+1)-2x-6=4x^2-20x+25;$$
$$4*x^2+8x+4-2x-6=4x^2-20x+25;$$
Перекинем все в левую часть, не забывая поменять знак:
$$4*x^2+8x+4-2x-6-4x^2+20x-25=0;$$
Поменяем местами слагаемые, чтобы было проще приводить подобные:
$$4x^2-4x^2+8x-2x+20x+4-6-25=0;$$
$$26x-27=0;$$
Как видите, все квадраты сократились, и уравнение превратилось в линейное:
$$26x=27;$$
$$x=\frac{27}{26};$$
Ответ: \(x=\frac{27}{26}.\)

Пример 3
$$\frac{x}{6}+\frac{x}{12}+x=-\frac{35}{4};$$
Домножим уравнение слева и справа на \(12\). Почему именно на \(12\)? Потому что в уравнении есть дроби с знаменателями \(6\), \(12\) и \(4\), на все эти числа \(12\) можно разделить:
$$12*(\frac{x}{6}+\frac{x}{12}+x)=12*(-\frac{35}{4});$$
$$12*\frac{x}{6}+12*\frac{x}{12}+12*x=12*(-\frac{35}{4});$$
$$2x+x+12x=-3*35;$$
$$15x=-105;$$
$$x=\frac{-105}{15}=-7;$$
Ответ: \(x=-7.\)

Подробнее про линейные уравнения можно почитать в отдельной статье.

Пример 4
$$(x-1)^2=2x^2-6x-31;$$
Раскроем скобки:
$$x^2-2x+1=2x^2-6x-31;$$
$$x^2-2x+1-2x^2+6x+31=0;$$
$$x^2-2x^2-2x+6x+1+31=0;$$
$$-x^2+4x+32=0;$$
После приведения подобных слагаемых в уравнении остался \(x^2\), а значит перед нами квадратное уравнение, которое можно решить через дискриминант:
$$a=-1; \quad b=4; \quad c=32;$$
$$D=b^2-4ac=4^2-4*(-1)*32=16+128=144=12^2;$$
$$x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-4+12}{2*(-1)}=\frac{8}{-2}=-4;$$
$$x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-4-12}{2*(-1)}=\frac{-16}{-2}=8;$$
Ответ: \(x=-4; \qquad x=8.\)

Другие теоремы

Кроме известных теорем, таких как теоремы Ферма, Ферма-Эйлера, Пуанкаре, Эйлера, Пифагора и других, в математике есть также много других теорем, пока еще не доказанных или не полностью доказанных.

Одной из таких теорем является гипотеза Римана, которая относится к теории функций комплексного переменного. Гипотеза утверждает, что все нетривиальные нули функции Римана расположены на прямой Re(s)=1/2. Эта теорема является одной из важнейших задач в математике и до сих пор не имеет подтверждения.

Также стоит упомянуть теорему Гольдбаха, которая гласит, что любое четное число можно представить в виде суммы двух простых чисел. Несмотря на многочисленные проверки теоремы, ее доказательства до сих пор не существует.

• Теорема Бейкера — Гилберта — Париса, относящаяся к логике первого порядка и невозможности доказать некоторые утверждения в теории множеств и арифметике.
• Миранда многомерной системы динамических уравнений, относящейся к теории динамических систем и имеющая связь с теорией хаотических процессов.

Все эти теоремы являются объектами изучения многих математиков со всего мира, и до сих пор остаются теоретическими задачами. Однако именно такие нетривиальные и не решаемые задачи существенно расширяют границы знаний и способствуют развитию математики.

Какие теоремы в математике до сих пор не доказаны?

Существует множество теорем в математике, которые до сих пор не доказаны. Одной из самых известных является гипотеза Римана, которая связана с распределением простых чисел. Также существуют нерешенные задачи в теории чисел, геометрии и логике.

Каковы последствия для области математики, если эти теоремы никогда не будут доказаны?

Если теоремы, которые не доказаны, останутся нерешенными, это может иметь огромные последствия для развития математики. Многие важные теории могут оказаться ошибочными или неполными, если не будет возможности доказать или опровергнуть эти нерешенные задачи.

Почему теоремы не доказаны?

Существует множество причин, почему теоремы в математике могут оказаться неразрешимыми. Некоторые из них связаны с техническими проблемами или сложностью математических проблем, другие — с недостатком информации, а другие — просто случайностью.

На сколько близко к доказательству эти теоремы?

Доказательства для некоторых нерешенных теорем могут быть очень близко, тогда как для других доказательства вряд ли найдутся в скором времени. Результаты компьютерных вычислений и экспериментов могут помочь в определении путей для доказательства, но это может занять много лет.

Каково значение этих нерешенных задач для математики?

Нерешенные задачи в математике имеют огромное значение для развития науки. Эти задачи могут оказаться испытанием для новых методов решения, стимулируя развитие техники. Кроме того, решение этих задач может привести к новым открытиям, которые возможны только благодаря раскрытию истинности утверждений, вытекающих из этих теорем.

Может ли решение этих задач изменить наше понимание мира?

К сожалению, мы не можем предсказать, каким образом решение этих задач может изменить наше понимание мира. Возможно, решение этих задач приведет к открытию новых принципов, которые изменят наше представление о мире. Это может привести к развитию новых технологий, новых открытий и многого другого.

Как математики работают над теоремами, которые не доказаны?

Математики продолжают работать над не доказанными теоремами, использованием различных методов и техник. Иногда они используют компьютеры для выполнения большого количества вычислений, позволяющих выявить закономерности. Другие методы включают работу в коллективе и обмен идеями с другими учеными.

Практическое применение дробей с нулевым значением

Дробь с нулевым значением, то есть дробь, у которой числитель равен нулю, обладает рядом особенностей, которые могут быть полезными в различных практических ситуациях.

Одним из распространенных применений дробей с нулевым значением является обобщение и упрощение дробных выражений. Например, при решении уравнений или систем уравнений может возникнуть необходимость в упрощении выражений, содержащих дроби, включая дроби с нулевым числителем. Упрощение выражений с помощью дробей с нулевым значением может значительно упростить дальнейшие математические операции.

Другим примером практического применения дробей с нулевым значением является использование их в программировании. Дробь с нулевым числителем может служить особой маркерной дробью, обозначающей отсутствие значения или невозможность выполнения некоторой операции. Например, при делении на ноль в программе можно использовать дробь с нулевым числителем для обработки исключительной ситуации.

Кроме того, в некоторых областях науки и техники, где возникают стремления к бесконечности или границам, дробь с нулевым значением может иметь смысл и использоваться для математического моделирования и анализа. Например, в теории вероятностей дробь с нулевым значениям может использоваться для представления событий, которые не могут произойти вообще.

Таким образом, дроби с нулевым значением имеют практическую пользу и могут применяться в различных областях. Они позволяют упрощать математические выражения, обрабатывать исключительные ситуации в программировании и строить математические модели

Важно понимать особенности и использование дробей с нулевым значением для достижения эффективного и верного результата в практических задачах