Погрешность измерительных трансформаторов тока
Трансформатор тока (ТТ) осуществляет преобразование переменного тока, характеризующегося токовыми и угловыми характеристиками. При этом образуется погрешность как по величине тока (токовая), так и по фазе (угловая). Вторичный ток ТТ не совпадает по фазе с первичным, угол сдвига между ними и является угловой погрешностью.
При этом в качестве токовой фигурирует относительная погрешность в процентах, в то время как угловая погрешность выражается в радианах или сантирадианах (срад), то есть является абсолютной.
Все средства измерения, включая измерительные трансформаторы, имеют определённый класс точности, характеризующий величину отклонения измеренного значения величины от действительного.
Класс точности ТТ, в соответствии с ГОСТ 7746—2001, представляет собой численное выражение допустимого отклонение результатов измерений при полной загрузке ТТ от действительной величины, выраженное в процентах.
Например, для ТТ класса точности 0,1 поверка осуществляется на трёх значениях токовой нагрузки и должна давать следующие результаты:
- при токе нагрузки 5% от номинального значения, отклонение по току не должно превышать ±0,4%, по углу — ±0,45 сантирадиан (срад);
- при загрузке 20% пределы токового отклонения ±0,2%, углового — ±0,24 срад;
- загрузка на 100 – 120% должна обеспечивать точность по току ±0,1%, по углу — ±0,15 срад.
Приведенные данные свидетельствуют о том, что точность измерения тока в большой степени определяется уровнем загрузки ТТ. Отсюда можно сделать вывод, что повышения точности измерений в условиях эксплуатации ТТ можно добиться, если добиться его загрузки на 100%.
В обозначении класса точности может присутствовать буква S, которая означает, что поверка данного ТТ должна проводиться на пяти нагрузочных точках. Например, если класс точности обозначен как 0,2S, характеристики при поверке должны быть следующими:
- для режима загрузки 1% от номинала отклонения тока допускается в пределах ±0,75%, угла — ±0,9 срад;
- 5-ти процентная загрузка даёт отклонения ±0,35% и ±0,45 срад;
- в точках, соответствующих загрузке на 20, 100 и 120%, действительное значение измеряемого тока находится в рамках ±0,2%, а угла — в пределах ±0,3 срад.
Таким образом, показатели точности измерений для ТТ с литерой S в обозначении класса точности соответствуют заявленным в более широком диапазоне нагрузок (от 20% до 120%).
Важность учета погрешности
При выполнении любых измерений, будь то в физике, химии или технике, необходимо учитывать возможность появления погрешностей. Это является одним из основных принципов научного метода и является неотъемлемой частью проведения любых экспериментов и опытов.
Погрешности могут возникать из-за множества факторов, таких как неточности измерительных приборов, ошибки оператора, атмосферные условия, а также расхождения между теорией и практикой.
Если погрешности не будут учитываться, то результаты эксперимента могут оказаться неверными, что может привести к серьезным последствиям, например, к авиакатастрофе или сбою в работе ядерной электростанции.
Учитывая все вышеперечисленные факторы, учет погрешности является крайне важным и необходимым для получения достоверных результатов.
| Тип погрешности | Описание |
|---|---|
| Случайная | Обусловлена неточностями измерительных приборов и не зависит от условий эксперимента. |
| Систематическая | Обусловлена ошибками в работе приборов и отклонениями от нормальных условий эксперимента. Эту погрешность можно учесть и уменьшить методами калибровки приборов. |
Таким образом, учет погрешностей позволяет получить более точные результаты эксперимента и придерживаться знаний научного метода.
Вопрос-ответ
Вопрос: Какие могут быть причины случайной погрешности?
Ответ: Причинами случайной погрешности могут быть шумы в электрической цепи, непостоянность условий при проведении измерений, случайные колебания в принимающей системе, искажения в записи данных и т.д.
Вопрос: Может ли случайная погрешность привести к неверным результатам?
Ответ: Да, случайная погрешность может привести к неправильным результатам измерений. Она вносит случайные колебания в показания, что может сильно исказить результат и мешает получить точный результат.
Вопрос: Как уменьшить сильную случайную погрешность?
Ответ: Чтобы уменьшить влияние сильной случайной погрешности, нужно провести большое количество измерений и взять среднее значение. Чем больше измерений, тем менее вероятно, что случайные колебания увеличат погрешность.
Вопрос: Можно ли полностью исключить случайную погрешность из измерений?
Ответ: Невозможно полностью исключить случайную погрешность из измерений. Она возникает из-за множества случайных факторов, не контролируемых в процессе измерения.
Главная — Полезно — Шаг за шагом: как эффективно обнаружить случайную погрешность в любых исследованиях
Комментарии
DarkKnight
5.0 out of 5.0 stars5.0
Neo89
5.0 out of 5.0 stars5.0
Статья очень полезна, теперь знаю, как найти случайную погрешность. Благодарю автора за объяснения.
Иван Иванов
5.0 out of 5.0 stars5.0
Однако, я хотел бы добавить, что в моей практике иногда возникают некоторые трудности с точным измерением значения переменной в эксперименте
И я считаю, что важно не только уметь находить случайную погрешность, но и уметь справляться с ней. Например, можно уменьшить влияние случайной погрешности, увеличивая число измерений или используя специальные математические методы обработки данных
Все в целом, я считаю эту статью очень полезной и наглядной, и рекомендую ее всем, кто интересуется этой темой.
Максим
5.0 out of 5.0 stars5.0
Я всегда считал, что погрешность это просто разница между результатом и ожидаемым значением. Но после прочтения этой статьи я осознал, что вопрос намного сложнее. Случайная погрешность это частичка погрешности, которая возникает из-за случайных факторов и которую нельзя устранить. Нашел много полезных советов, где искать случайную погрешность
Особенно важно понимать это для тех, кто работает с измерительной техникой. Я бы хотел отметить, что данная статья очень доступна и понятна даже для тех, кто раньше не сталкивался с этой темой
Это большой плюс, так как она заинтересует широкую аудиторию. Мне понравилась структура статьи и то, как автор объясняет все тонкости этого вопроса. Рекомендую прочитать всем тем, кто хочет получить более глубокое понимание этой темы. PS: Один косяк на самом деле в статье есть. В одном месте есть опечатка. Но не существенная.
Александр
5.0 out of 5.0 stars5.0
Читая статью, я узнал, что случайная погрешность – это ошибка, которая возникает в любом измерении, даже при тщательном выполнении всех условий измерения. В статье очень хорошо описаны способы нахождения случайной погрешности, а также объяснено, какие факторы могут ее вызывать. Большое спасибо авторам за полезную информацию!
Петр Петров
5.0 out of 5.0 stars5.0
Статья очень помогла мне разобраться в том, как найти случайную погрешность. Рекомендую!
Инструменты для определения случайной погрешности
Существует несколько инструментов, которые могут помочь в определении случайной погрешности измерений. Один из них — это среднеквадратическое отклонение (СКО).
СКО — это статистическая мера, которая показывает, насколько данные распределены вокруг своего среднего значения. Она может быть использована для определения случайной погрешности в измерениях.
Еще один инструмент — это стандартная ошибка (SE). Она вычисляется путем деления СКО на квадратный корень из количества измерений. Данный инструмент позволяет оценить точность измерений.
| Измерение | Результат |
|---|---|
| Среднее значение | 10.14 |
| СКО | 0.28 |
| Стандартная ошибка | 0.125 |
| 1 | 10.2 |
| 2 | 9.8 |
| 3 | 10.5 |
| 4 | 9.9 |
| 5 | 10.3 |
Использование данных инструментов является важным этапом в определении случайной погрешности. Однако, следует учитывать, что для точных результатов необходимо провести несколько измерений.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения измеряемой величины. Для этого разделим 0,5 мм на 706 мм
В результате получим:
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины: и указывает на качество измерения. Ее можно выразить в процентах.
Пути снижения погрешности трансформаторов тока
Точность измерений ТТ напрямую связана с его характеристикой намагничивания. Для обеспечения наиболее высокой точности, ТТ должен работать в пределах прямолинейного участка кривой намагничивания. Существует два основных пути повышения точности:
- обеспечение оптимальной загрузки ТТ, относящееся к эксплуатационным мероприятиям;
- конструктивные усовершенствования ТТ, связанные в первую очередь с использованием сердечников с улучшенными магнитными характеристиками.
Существуют также способы коррекции отрицательной токовой погрешности, заключающиеся в уменьшении номинального числа витков вторичной обмотки ТТ. Это мероприятие повышает величину тока вторичной обмотки, приводящее к коррекции погрешности в сторону увеличения. Иногда такая мера может даже привести к изменению знака на противоположный.
Проверка и калибровка измерительных приборов
Правильная работа измерительных приборов основана на их точной калибровке и регулярной проверке. Эта процедура позволяет убедиться в том, что приборы работают с высокой точностью и минимальными случайными погрешностями. В данном разделе мы рассмотрим, как правильно проверять и калибровать измерительные приборы для достижения наилучших результатов.
1. Проверка прибора на заводские дефекты: перед использованием нового измерительного прибора необходимо проверить его на наличие заводских дефектов или скрытых повреждений. Это можно сделать путем проведения нескольких тестовых измерений с использованием эталонных значений. Если прибор показывает существенные отклонения от ожидаемых значений, следует обратиться к производителю для замены или ремонта.
2. Периодическая калибровка: калибровка измерительных приборов должна проводиться регулярно в соответствии с рекомендациями производителя или стандартными методиками. Калибровка позволяет установить соответствие показаний прибора эталонным значениям и внести необходимые корректировки. Частота калибровки зависит от типа прибора, его точности и чувствительности. Обычно рекомендуется проводить калибровку каждые 6-12 месяцев.
3. Использование эталонных значений: при проведении калибровки необходимо использовать эталонные значения, которые имеют известную точность и отслеживаемость. Эталоны можно получить у аккредитованных лабораторий или узлов метрологии. Использование эталонных значений позволяет свести к минимуму возможные погрешности и обеспечить высокую точность измерений.
4. Регулярная проверка прибора на стабильность: помимо калибровки, рекомендуется регулярно проверять прибор на его стабильность и отсутствие смещения по времени. Для этого можно провести несколько повторных измерений с использованием одного и того же значения и сравнить результаты. Если прибор показывает значительное изменение показаний со временем, возможно потребуется дополнительная настройка или ремонт.
5. Ведение документации и архивирование результатов: не менее важным шагом является ведение документации и архивирование результатов проверок и калибровок. Это позволяет отслеживать историю работы прибора, проведенные корректировки и изменения. Также в случае возникновения споров или несоответствий в показаниях прибора, наличие документации помогает установить причину и принять соответствующие меры.
В заключение хотелось бы отметить, что проверка и калибровка измерительных приборов являются неотъемлемой частью их эксплуатации. Правильная настройка и регулярное обслуживание приборов способствуют повышению точности измерений и уменьшению случайных погрешностей.
Анализ систематических ошибок для их минимизации
Анализ систематических ошибок включает следующие этапы:
- Идентификация ошибок: необходимо провести анализ методик и условий измерения, выявить возможные источники систематических ошибок. Это может быть несоответствие измерительных приборов стандартам, влияние окружающей среды и другие факторы.
- Оценка величины ошибок: провести измерения с использованием различных методик и измерительных приборов для определения величины систематических ошибок. Для этого могут использоваться стандартные образцы, проведение контрольных измерений и другие методы.
- Устранение ошибок: на основе данных, полученных на предыдущем этапе, принять меры по устранению систематических ошибок. Это может включать калибровку измерительных приборов, коррекцию методики измерения, создание специальных условий для проведения измерений.
- Контроль и верификация: после устранения систематических ошибок необходимо провести контрольные измерения для проверки эффективности принятых мер. Для этого могут использоваться стандартные образцы и методики.
Анализ систематических ошибок требует внимательного исследования и профессионального подхода. Правильное проведение данного анализа позволяет уменьшить влияние систематических ошибок на результаты измерений и повысить точность и достоверность получаемых данных.
Таблица 1: Пример оценки величины систематической ошибки
| Измерительный прибор | Методика измерения | Величина систематической ошибки |
|---|---|---|
| Осциллоскоп | Измерение амплитуды сигнала | ±0.1 В |
| Мультиметр | Измерение сопротивления | ±0.01 Ом |
| Термометр | Измерение температуры | ±0.5 °C |
Таблица 1 показывает пример оценки величины систематической ошибки для различных измерительных приборов и методик измерения. Полученные значения могут быть использованы для выбора наиболее точных приборов и определения корректировок, необходимых для минимизации систематических ошибок.
Применение результатов
Получение случайной погрешности является важной задачей при проведении измерений и экспериментов. Анализ этой погрешности позволяет определить точность и достоверность полученных результатов
Кроме того, знание случайной погрешности позволяет более эффективно планировать эксперименты и выбирать методы измерений.
Применение результатов анализа случайной погрешности может быть различным. Например, в процессе разработки новых продуктов или технологий анализ погрешности может помочь выбрать наиболее точные и надежные методы измерений, что увеличит качество и эффективность продукта или технологии.
Также анализ случайной погрешности может быть полезен в научных исследованиях. Здесь это помогает установить степень точности полученных данных и проверить их достоверность. На основе такой проверки можно принимать правильные решения, например, о принятии или отбрасывании гипотезы о некотором явлении.
Применение метода наименьших квадратов для устранения случайной погрешности
Процесс применения метода наименьших квадратов включает следующие шаги:
- Формулировка математической модели, описывающей зависимость между измеряемыми переменными.
- Сбор экспериментальных данных, включающих измерения зависимой и независимых переменных.
- Подбор параметров модели таким образом, чтобы сумма квадратов отклонений между наблюдаемыми и предсказанными значениями была минимальной.
- Оценка точности предсказаний и анализ полученных результатов.
Метод наименьших квадратов широко применяется в различных областях, где требуется устранение случайной погрешности. Например, он может быть использован для аппроксимации экспериментальных данных, построения регрессионных моделей, решения систем линейных уравнений и т.д.
Один из главных преимуществ метода наименьших квадратов заключается в том, что он дает оптимальное решение в случае линейной модели с нормально распределенными ошибками. Однако, при применении этого метода необходимо учитывать некоторые условия, такие как линейность зависимостей и отсутствие систематической погрешности.
В итоге, применение метода наименьших квадратов позволяет получить более точные и надежные результаты измерений, позволяя устранить случайную погрешность и улучшить качество данных.
Подбор статистических методов и контрольных мер для уменьшения случайной погрешности в измерениях
Для достижения высокой точности при измерении физических величин необходимо учитывать не только случайную погрешность, но и систематическую погрешность. Однако в данном разделе рассмотрим способы уменьшения случайной погрешности в измерениях путем подбора статистических методов и контрольных мер.
Один из основных методов уменьшения случайной погрешности — повторение измерений. Чем больше измерений проводится, тем точнее будет получен результат. Полученные значения можно использовать для вычисления среднего значения и стандартного отклонения. При наличии большого числа измерений статистическая погрешность будет существенно меньше.
Для учета случайной погрешности при подборе статистических методов необходимо учитывать характеристики измеряемых величин. Если случайная погрешность имеет нормальное распределение, то используют методы математической статистики, основанные на этом предположении. Например, можно применить методы наименьших квадратов для подбора линейной функции в экспериментальных данных.
Кроме того, для уменьшения случайной погрешности необходимо применять контрольные меры. Одна из таких мер — повторяемость измерений. При повторении измерений их результаты должны быть близки к предыдущим значениям с небольшим разбросом. Если разброс значений слишком велик, это может указывать на проблемы со случайной погрешностью и требовать корректировки методики измерений.
Также можно применять методы контроля качества измерений, такие как контрольные образцы и проверка рабочих стандартов. Контрольные образцы представляют из себя известные величины, которые используются для проверки точности измерения. Проверка рабочих стандартов позволяет убедиться, что используемые приборы соответствуют принятому стандарту и работают с высокой точностью.
| Метод | Описание |
|---|---|
| Повторение измерений | Проведение большого числа измерений для получения более точных результатов |
| Методы математической статистики | Использование методов наименьших квадратов и других статистических методов для обработки данных |
| Повторяемость измерений | Контроль за разбросом результатов при повторении измерений |
| Контрольные образцы | Использование известных величин для проверки точности измерений |
| Проверка рабочих стандартов | Убедиться, что используемые приборы соответствуют принятому стандарту и работают с высокой точностью |
Точность измерений и погрешности в физике — определение и формулы с примерами
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины
Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
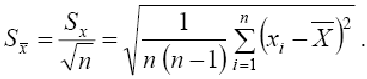
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Как избежать случайных погрешностей при измерениях
1. Правильное обращение с измерительными приборами
Одной из основных причин случайных погрешностей является неправильное обращение с измерительными приборами. Для достижения точных результатов необходимо следовать инструкциям по эксплуатации приборов, обеспечивать их правильную калибровку и хранение. Также следует избегать ударов и других механических воздействий на приборы, а также избегать эксплуатации приборов в условиях, которые могут повлиять на результаты измерений (например, сильные магнитные поля).
2. Повторяемость измерений
Одним из способов уменьшения случайных погрешностей является повторяемость измерений. При повторном измерении одной и той же величины несколько раз и последующем усреднении результатов можно снизить случайные погрешности
Это особенно важно при измерении низких значений или малых изменений величин
3. Использование усреднения
Усреднение результатов измерений позволяет снизить случайные погрешности и увеличить точность измерений. Для этого необходимо проводить несколько измерений одной и той же величины и вычислять среднее значение. Чем больше измерений, тем точнее будет полученный результат.
4. Контроль внешних условий
Случайные погрешности могут быть вызваны воздействием внешних условий на измерительные приборы. Для уменьшения этих погрешностей следует контролировать их влияние. Например, если температура окружающей среды может влиять на измеряемую величину, необходимо поддерживать постоянную температуру в помещении. Также следует избегать воздействия внешних электромагнитных полей и вибраций на измерительные приборы.
5. Калибровка и проверка приборов
Калибровка и проверка измерительных приборов являются важными шагами для уменьшения случайных погрешностей. Периодическая калибровка приборов позволяет установить их точность и скорректировать показания, если это необходимо. Также регулярная проверка приборов на работоспособность и правильность измерений помогает выявить возможные проблемы и исключить случайные погрешности.
Избежать полностью случайных погрешностей при измерениях невозможно, однако с применением этих способов можно существенно уменьшить их влияние. Правильное обращение с приборами, повторяемость измерений, усреднение результатов, контроль внешних условий, калибровка и проверка приборов играют важную роль в достижении более точных результатов измерений.





























