Алгебра логики и решение задач
Несмотря на то, что логика, как наука о размышлении, существовала еще 5 в. До н.э., теперь это важная часть многих наук, а не только философии и риторики. Также логика существует, как отдельная наука уже более 200 лет.
Инструменты алгебры логики позволяют переводить словесные высказывания в сухие, объективные выражения, а с их помощью выполнять различные логические операции.Появился этот раздел математики 200 лет назад.
Стоит остановиться на базовых понятиях алгебры логики:
- константы (0,1);
- переменные;
- формула;
- знаки операций;
- скобки.
Логическая переменная – обозначение логического выражения, которое может быть true (t, правда, истина, да, 1) – false (f, ложь, нет, 0).
Формула– символьный способ выражения операции между переменными при помощи специальных знаков и скобок ().
Логическое высказывание – утверждение, в котором говорится только правда или только ложь.
Образец таких предложений: «Луна – вертится вокруг Марса» – ложно, а «После зимы всегда приходит весна» – истинно.
Частицы «не», «или», если», «и» и другие, которые являются связующими элементами в обычной речи, позволяют создавать элементарные логические выражения.
Элементарные высказывания – те, к которым нельзя применить понятие истинности или ложности. Их обозначают различными символами (латинские буквы, цифры), знаками. Ими занимаются те сферы, к которым они относятся. Они входят в состав высказываний логики.
Из одних высказываний можно образовывать другие, в результате получая составные высказывания. И от того, являются исходные элементы составного конечного высказывания правдивыми или неправдивыми, а также какие логические связки использовались, будет правдой или ложью все высказывание в целом.
Чтобы образовать такое составное предложение в обычной жизни, используют связки И, ИЛИ, НЕ. А научный подход заменил их на конъюнкцию, дизъюнкцию, инверсию и более сложные операции. Все эти процессы выражают словесно, таблично (таблицы истинности) или графически (диаграммы Эйлера-Венна).
Простые выражения содержат лишь одно выражение (правдивое или нет), и не содержит никаких логических операций.
Сложные могут содержать от 2 и больше аргументов (простых выражений), которые между собой связаны логическими операциями.
Еще используют понятие «предикат» – содержит любое количество переменных без перечисления всех составляющих данных. Это предикат простых, отрицательных P(x)=(x<0) чисел.
Чтобы исключить лишнюю информацию, оставив только логические связи, используют таблицы истинности, наглядно демонстрирующие, правдиво или неправдиво конечное предложение, если учесть все значения входящих в его состав простейших частей.
Такая форма оформления и решения задач используется в построении электросхем, для решения различных логических задач, в булевой алгебре, программировании.
Основные операции
Количество логических операций, которыми обычно оперирует логика 6:
- Отрицание.
- Умножение.
- Сложение
- Следование.
- Дизъюнкция.
- Равнозначность.
Остановимся на каждом из них детальнее, выясним как правильно они называются в алгебре логики, есть ли у них аналоги в обычной речи, в математике, и как их можно использовать в обычной жизни.
Отрицание или инверсия
Операция отрицания или НЕлогическое, корректнее будет название инверсия.Конечное высказывание будет противоположным первоначальному (исходному). Применяется для одного выражения, которое может быть как сложным, так и элементарным.
На примере этой простейшей операции удобно показывать, насколько лаконичны и информативны таблицы истинности. Обозначим исходное высказывание буквой А, соответственно, окончательное будет не А (или НЕ, ‾, ˥ not А). А их ложность или правдивость напишем при помощи цифр 0 и 1.
Получается, если исходное значение правда, то новое будет ложь, и наоборот.
Умножение или конъюнкция &
Логическое И или умножение еще называют конъюнкцией. Финальное высказывание будет правдивым, только если его составляющие тоже правдивы. Во всех остальных случаях оно будет ложным. Применяется для двух и более аргументов, элементарных или сложных. Обозначение А и В; А ^ В; А &В; A and В.
Как видно, при помощи таблицы истинности из 15 ячеек можно описать то, на описание чего при помощи слов пришлось бы потратить минимум 5 полноценных предложений.
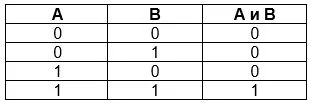
Логическое И в обычной жизни:
- Хорошая певица должна быть талантливой и упорной (наличие только одного качества не позволит проявить миру свой талант).
- По условиям задачи А – число меньше 30, В – число делиться на 3. Нужно найти решение А ˄ В.
Решение: Первое множество содержит числа 1,2,3….29. Второе – 3,6,9,…27. Решением будет множество на пересечении множеств А и В, что хорошо покажут диаграммы Эйлера-Венна. А ˄ В будет истинным для множества чисел 3,6,9,….27.
Сложение или дизъюнкция V
Логическое ИЛИ, сложение по-другому называют дизъюнкцией. Оно истинно всегда, кроме случая, если ложны все составные высказывания. Функция распространяется на простые и сложные исходные аргументы. Обозначение А или В; A v В; А ог В.
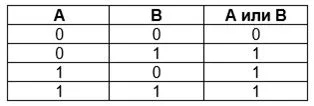
В обычной жизни нас окружает логическое ИЛИ:
- «Чтобы сдать тесты на «отлично», нужно старательно готовиться ИЛИ должно повезти с билетом».
- Есть задача с 2-мя условиями: А – число делится на 5, В – число делится на 2.
Решение: Первое множество чисел включает в себя 5, 10, 15…Второе – 10, 20, 30…Решение, при котором истинно Аv В – совокупность обеих множеств (5, 10, 15, 20, 25, 30…).
Следование или импликация
Для этого случая важно значение каждого выражения и даже его очередность, потому что первый аргумент считается условием, второй – следствием. Импликация будет ложной лишь в одном случае – если первое составляющее правдиво, а второе нет
Такое логическое следование имеет аналог в обычной речи «если.. то», то есть одно событие зависит от другого. Символьно связи выражают следующим образом:
![]()
Логическое следование в обычной жизни:
- Если пойти к врачу, можно выздороветь (но можно выздороветь и без похода к врачу, а можно и после визита в больницу не выздороветь).
- По условию задачи, А – если число делится на 10, то В делится на 5.
Строгая дизъюнкция
Такая логическая операция выдаст истину, если любое из составляющих высказываний будет истинным, независимо очередности.
Это пример исключающей функции. Аналог в словесном выражении – «либо». Разница от простой дизъюнкции в том, что конечное выражение будет истинным, только если будет правдой одна переменная.
![]()
Эквиваленция или равнозначность
Операция, выдающая истину в случае, если обе исходные переменные истины или неправдивы.Обозначают А ~В, А В.
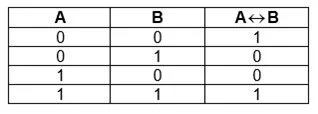
Словесная аналогия – «тогда и только тогда, когда», математическая – «необходимо и достаточно». Если сравнить таблицы истинности для предыдущих операций, очевидно, что она противоположна «исключающему ИЛИ», то ее можно посчитать так:
Пример эквивалентности из обычной жизни:
- Если вечером на горизонте солнце темно-красного цвета, значит, завтра будет ветреный день.
- В задаче 2 условия: А – сумма цифр числа равно 9, В – число делится на 9. АВ означает, что число делится на 9, если сумма цифр равна 9.
Операция «Равносильность» — каковы ее особенности?
Данная операция может быть представлена с помощью символа «≡» или «⇔». Операция «Равносильность» используется для сравнения двух высказываний на равносильность, то есть на то, являются ли они логически эквивалентными. Если два высказывания имеют одинаковые значения истинности для всех входных комбинаций, то они считаются равносильными.
Основными особенностями операции «Равносильность» являются:
- Возможность определения логической эквивалентности двух высказываний.
- Возвращение значения «истина» только в случае, если оба высказывания истинны или оба ложны.
- Возвращение значения «ложь» во всех остальных случаях.
- Использование символов «≡» или «⇔» для представления операции «Равносильность».
Операция «Равносильность» широко используется в логике, математике, информатике и других науках. Она позволяет логически сравнивать высказывания и определять их эквивалентность
Понимание особенностей и правил операции «Равносильность» особенно важно при выполнении логических операций и построении логических выражений
Высказывание и операции над высказыванием
Исходным (базовым) понятием является простое высказывание.
Под высказыванием обычно понимают всякое предположение, утверждающее что-либо о чем-либо. Если смысл,
содержащийся в высказывании, соответствует
действительности, то высказывание является истинным, иначе
ложным.
Обычно элементарные высказывания обозначают строчными буквами латинского алфавита $a$, $b$, $c$,
$x$, $y$ …, которые являются логическими переменными в логических формулах. Истинные
значения обозначаются
буквой И (True, T) или 1, а ложные – Л (False, F) или 0.
Бинарные функции
$n = 2$ — количество аргументов.
$k_n = 2^2 = 4$
$k_ф = 2^4 = 16$
| $x$ | $y$ | $f_0$ | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ | $f_{10}$ | $f_{11}$ | $f_{12}$ | $f_{13}$ | $f_{14}$ | $f_{15}$ |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| const «0» | $x \land y$ | пер. $x$ | пер. $y$ | $x \xor y$ | $x \lor y$ | const «1» |
Номер функции совпадает с двоичной записью функции
- $f_1$ — коньюнкция. $x \& y$ — $x$ и $y$ — ${x} and {y}$ $x \&\& y$
- $f_7$ — дизъюнкция. $x | y$ — $x$ или $y$
- $f_{11}$ и $f_{13}$ — импликация (следование)
- $f_9$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
- $f_6$ — равнозначность, эквивалентность, равносильность. ${x} \equiv {y}$
Из элементарных высказываний можно составить более сложные с помощью логических связок:
- $\lnot$ — логическое «не» (отрицание)
- $\land$ — логическое «и» (конъюнкция) — «и одновременно»
- $\lor$ — логическое «или» (дизъюнкция)
- $\Rightarrow$ — «логическое следствие» (импликация)
- $\equiv$ — «эквивалентность»
- круглых скобок (, ) — групировка операций.
- …есть и другие (менее распространённые) связки…
Логические связки
можно определить с помощью таблицы истинности. В левой части этой таблицы перечисляются
все
возможные
комбинации значений логических переменных $x$ и $y$. В правой части – соответствующие им им значения выражений из
переменных и логических связок.
| $x$ | $y$ | $\lnot x$ | $x \land y$ | $x \lor y$ | $x \Rightarrow y$ | $x \equiv y$ |
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 |
Связки имеют следующий приоритет: $\lnot \land \lor \Rightarrow \equiv$ (приоритет можно изменить с помощью скобок).
Высказывания (формулы) из простых высказываний, связок и скобок, называют правильно построенными формулами
или просто формулами.
Значение логических связок близко к соответствующим высказываниям на
естественном языке. Например смысл связок $\lnot$ и $\land$ практически
совпадает со смыслом слов «не» и «и». Однако имеются и некоторые различия. Так формула
$x \lor y$ несколько шире, чем русское «$x$ или $y$».
Выражение «$x$ или $y$» по смыслу это формула $x \land \lnot y \lor \lnot x \land y$ (исключающее или). Еще больше
различий между семантикой
формулы $x \Rightarrow y$ в логике высказываний и выражению «из $x$ следует $y$». В русском языке это выражение
истинно, если истинны $x$ и $y$, т.е. предложение русского языка по смыслу совпадает с формулой $x \land y$.
Логическое следствие истинно также, если $x$ и
$y$ ложны или $x$ ложна, а $y$ истинна. Логическую формулу $x \Rightarrow y$ следует
интерпретировать на естественном языке так: «Если $x$ истинна, то $y$ тоже истинна, а остальное
неизвестно».
Таблица истинности — таблица в которой в левой части перечислены все возможные значения переменных, а в правой
части значения функции. Для построения таблицы истинности выписываются все возможные значения аргументов, а потом
поэтапно вычисляем значения.
Для любой формулы также можно написать таблицу истинности. Например:
| $x$ | $y$ | $\lnot x$ | $\lnot y \lor y$ | $\lnot x \land (\lnot y \lor y)$ | $\lnot x \land (\lnot y \lor y) \Rightarrow \lnot x$ |
| 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | ||||
| 1 | 1 | 1 |
Если формула содержит $n$ переменных, то в таблице истинности будет $2^n$
строк (в примере формула содержит 2 переменные и $2^2 = 4$ строки). Кроме того, данная формула истинна на
любом наборе значений своих переменных (везде 1). Такие формулы называются тождественно истинными или
тавтологиями. В противоположной ситуации, формула является тождественно ложной или
невыполнимой. Если две разные формулы принимают одинаковые значения на любом наборе значений переменных, то
такие формулы называют равносильными. Равносильные формулы обозначаются знаком равенства =.
Расширенные логические операции
Одной из расширенных логических операций является импликация (логическое ПРИМЕЧАНИЕ), которая определяет, когда одно высказывание является следствием другого. Операция импликации обозначается символом «→» и выражается следующим образом: «A → B», где A и B — логические значения. Результат операции импликации будет истинным только в том случае, если A ложно или B истинно.
Еще одной важной расширенной логической операцией является эквивалентность (логическое РАВЕНСТВО), которая определяет, когда два высказывания являются равными. Операция эквивалентности обозначается символом «» и выражается следующим образом: «A B», где A и B — логические значения
Результат операции эквивалентности будет истинным только в том случае, если либо оба значения A и B истинны, либо оба значения ложны.
Также стоит упомянуть операцию исключающего ИЛИ (XOR), которая определяет, когда одно из двух высказываний истинно, а другое ложно. Операция XOR обозначается символом «⊕» и выражается следующим образом: «A ⊕ B», где A и B — логические значения. Результат операции XOR будет истинным только в том случае, если A и B имеют противоположные значения.
Эти расширенные логические операции позволяют более точно определить связи между логическими значениями и применять их при анализе и построении логических выражений.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
1. Рассмотрим высказывание «Умение и настойчивость приводит к достижению цели». Достижение цели возможно только при одновременной истинности двух предпосылок — умения И настойчивости.
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
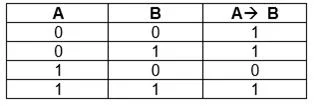
Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:
| A | B | А → B |
| 1 | ||
| 1 | 1 | |
| 1 | ||
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Приведем примеры операции следования.
1. Рассмотрим высказывание «Если идет дождь, то на улице сыро». Здесь исходные высказывания «Идет дождь» и «На улице сыро». Если не идет дождь и не сыро на улице, результат операции следования — истина. На улице может быть сыро и без дождя, например, когда прошла поливочная машина или дождь прошел накануне. Результат операции ложен только тогда, когда дождь идет, а на улице не сыро.
2. Рассмотрим два высказывания: А {х делится на 9}, В {х делится на 3}. Операция А → В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты:
■ А — ложно, В — ложно (1-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то и В — ложно». Например, х = 4, 17, 22.
■ А — ложно, В — истинно (2-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то В — истинно». Например, х = б, 12, 21.
■ А — истинно, В — ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации.
■ А — истинно, В — истинно (4-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — истинно, то и В — истинно». Например, х = 9, 18, 27.
Операция «ИЛИ» — как правильно использовать?
Использование операции «ИЛИ» особенно полезно в условных операторах и циклах. Она позволяет задать условие, при котором как минимум одно из условий должно быть истинным для выполнения определенного кода или действия.
Правильное использование операции «ИЛИ» заключается в следующих моментах:
- Убедитесь, что вы правильно размещаете оператор «ИЛИ» между операндами. Внимательно проверьте порядок и расстановку скобок, чтобы избежать ошибок в логике вашего кода.
- Используйте операцию «ИЛИ» с различными сочетаниями условий для достижения нужного результата. Это может включать комбинирование логических операторов, таких как «И», «ИЛИ НЕ» и «НЕ», для более сложных проверок.
- Не забывайте о приоритете операций. Операция «ИЛИ» имеет более низкий приоритет, чем операция «И», поэтому вам может потребоваться использовать скобки для явного указания приоритета операций.
Корректное использование операции «ИЛИ» позволяет создавать более гибкий и управляемый код. Однако не злоупотребляйте ее использованием, чтобы не усложнять код и сделать его более понятным для других разработчиков.
Операция «Импликация» — как она работает с двумя значениями?
Импликация: Если исходное значение истинно, то следующее значение также истинно. В противном случае, если исходное значение ложно, то результат операции тоже ложен.
Импликация может быть сформулирована с помощью примера: «Если сегодня идет дождь, то улицы мокрые». Здесь исходное значение — «сегодня идет дождь», а следующее значение — «улицы мокрые». Если исходное значение истинно (сегодня действительно идет дождь), то следующее значение также истинно (улицы будут мокрыми). В случае, если исходное значение ложно (сегодня нет дождя), то следующее значение будет ложным (улицы не будут мокрыми).
Операция «Импликация» является одной из основных операций в логике и находит широкое применение в математике и информатике, особенно при формулировании условий и выражений с помощью логических операций.
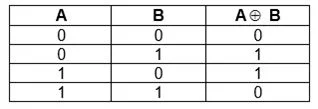
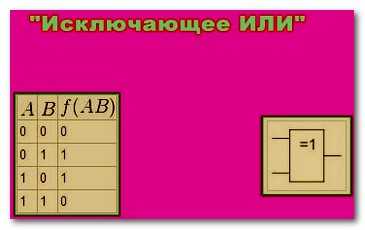
Операция «Исключающее ИЛИ» — для чего нужно?
Операция XOR широко используется в различных областях информатики и электроники. Несмотря на свою простоту и общую концепцию, XOR имеет множество полезных применений.
Одной из наиболее распространенных областей применения операции XOR является криптография. В криптографии XOR используется для шифрования и дешифрования данных. При использовании XOR с ключом или «маской» можно преобразовывать данные таким образом, что без знания ключа будет сложно прочитать или взломать зашифрованную информацию.
Операция XOR также используется в программировании и логике. Например, при проверке целостности данных XOR может использоваться для определения различий между двумя наборами данных. Также операция XOR может использоваться для инвертирования значений — если значение равно истине, то операция XOR с этим значением приведет к ложному и наоборот.
Кроме того, операция XOR может быть использована для реализации булевых функций, таких как AND, OR и NOT, что позволяет сократить количество логических элементов или составить более компактный код.
Таким образом, операция «Исключающее ИЛИ» имеет широкий спектр применения и является важным инструментом в области информатики, электроники и программирования.
Основные логические операции
Существует три основных логических операции при помощи которых можно записать любое логическое выражение (не пугайтесь)
1. Инверсия2. Конъюнкция3. Дизъюнкция
Конъюнкция, оно же «Логическое И», оно же «Логическое умножение».
Мы выбираем название «Логическое И» – оно чаще встречается в программировании.
Допустим, у нас есть два простых выражения – А и В. Эти выражения могут иметь значения или 1 (истина), или 0 (ложь). При выполнении операции «Логическое И» мы получим сложное выражение которое примет значение 1 (истина) только в том случае если и А, и В имеют значение 1 (истина), во всех других случаях результат будет 0 (ложь).
Операция «Логическое И» имеет обозначения (в языках программирования): И, &&, AND, &.
Дизъюнкция, оно же «Логическое ИЛИ», оно же «Логическое сложение».
Мы выбираем название «Логическое ИЛИ». Кстати, если логически подумать, то можно и догадаться какие результаты будут при выполнении этой операции.
В «Логическом И» результат равен 1, если и А, и В, равны 1, а в «Логическом ИЛИ» результат будет равен 1, если или А, или В, равны единице.
Операция «Логическое ИЛИ» имеет обозначения: ИЛИ, ||, OR, |.
Инверсия, оно же «Логическое НЕ», оно же «Отрицание».
Мы выбираем название «Логическое НЕ».
Операция «Логическое НЕ» имеет обозначения: НЕ, !, NOT.
Тут вообще все просто:
Если А=1 (истина), то после выполнения операции «Отрицание» А примет значение 0, то есть становится ложным. И наоборот.
Есть еще одно название этой операции «Инвертор», а применяется оно в отношении цифровых микросхем.
В программировании часто применяется еще одна логическая операция – симбиоз «Логического И» и «Логического ИЛИ»:Строгая дизъюнкция, оно же «Исключающее ИЛИ», оно же «Логическое сложение, исключающее ИЛИ», оно же «Сложение по модулю 2»
Мы выбираем название «Исключающее ИЛИ»
Операция «Исключающее ИЛИ» имеет обозначения: Искл.ИЛИ, XOR, ^.
В этом случае, при выполнении операции «Исключающее ИЛИ», результат будет истинен (равен 1), если А не равно В. В остальных случаях результат будет равен 0 (ложный).
Законы алгебры логики
В логике высказываний известно много общезначимых формул, которые также называются законами логики
высказываний. Основными законами являются следующие:
- законы идемпотентности (повторение действия над объектом не изменяет его, латинский idem — «тот же
самый»
и potens — «способный»):- $x \land x = x$
- $x \lor x = x$
- $x \land 1 = x$ — $x$ и Истина всегда будет $x$
- $x \lor 1 = 1$ — $x$ или Истина всегда будет Истина
- $x \land 0 = 0$
- $x \lor 0 = x$
- $x \land \lnot x = 0$ – закон противоречия
- $x \lor \lnot x = 1$ – закон исключения третьего
- $\lnot \lnot x = x$ – закон снятия двойного отрицания
- законы поглощения
- $x \land (y \lor x) = x$
- $x \lor (y \land x) = x$
Доказать эти и последующие законы можно с помощью построения таблиц истинности или
простейших логических рассуждений.
Следующая группа законов представляет взаимосвязь между логическими операциями:
- $(x \equiv y) = (x \Rightarrow y) \land (y \Rightarrow x)$
- $x \Rightarrow y = \lnot x \lor y$
- законы Де Моргана
- $\lnot(y \lor x) = \lnot y \land \lnot x$
- $\lnot(y \land x) = \lnot y \lor \lnot x$
Замечательным следствием приведенных выше законов является следующий факт. Любую логическую формулу можно заменить
равносильной ей, но содержащую только две логические операции:
- конъюнкцию «и» и отрицание «не»
- дизъюнкцию «или» и отрицание «не»
Дальнейшее исключение логических операций, очевидно, невозможно, то есть приведенные пары представляют минимальный
базис для построения правильно построенных формул. Однако существует операция, с помощью которой можно представить
любую логическую связку. Эта операция получила название «штрих Шеффера» и определяется следующим образом:
| $x$ | $y$ | $x | y$ |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
На основании этого определения можно ввести следующие законы, выражающие взаимосвязь операции «штрих Шеффера» и
других логических связок:
- $\lnot x = x | x$ — связка «не» через «штрих Шеффера»
- $x \land y = (x | y) | (x | y)$ — связка «и» через «штрих Шеффера»
Также следует отметить, что $x | y= \lnot (x \lor y)$.
К основным законам алгебры логики также относятся следующие:
- коммутативные законы (от перестановки мест результат не меняется)
- $x \land y = y \land x$
- $х \lor y = y \lor x$
- дистрибутивные законы (правила группировки)
- $x \land (y \lor z) = (x \land y) \lor (x \land z)$
- $x \lor (y \land z) = (x \lor y) \land (x \lor z)$
- ассоциативные законы
- $x \land (y \land z) = (x \land y) \land z$
- $x \lor (y \lor z) = (х \lor y) \lor z$
С помощью законов логики можно осуществлять равносильные преобразования. Такие преобразования используются для
доказательств, приведения формул к заданному виду, упрощения формул.
Под сложностью формул обычно понимается количество символов, используемых для ее записи. То есть формула $\alpha$
проще
формулы $\beta$, если $\alpha$ содержит меньше букв и логических операций. Например, для формулы
$(\lnot (x \lor y) \Rightarrow x \lor y) \land y$
можно записать следующую цепочку преобразований, приводящих ее к более простому виду:
$(\lnot \lnot(x \lor y) \lor x \lor y) \land y = (x \lor y \lor x \lor y) \land y = (x \lor y) \land y = y$.
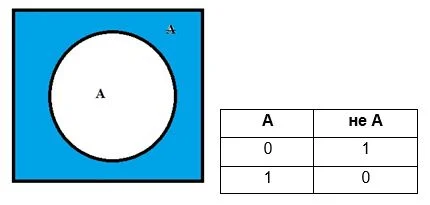
Диаграммы Эйлера-Венна
Тем, кто лучше воспринимает информацию в виде изображений, понравятся диаграммы Эйлера-Венна, которые показывают, как пересекаются множества между собой.
Число пересечений (областей) можно посчитать сразу, оно равно n = 2N, где N – число множеств. Так как значение двойки в степени растет очень быстро (4,8,16), обычно диаграммы используют для 2-3 множеств. Далее области пересечения будут сливаться, образуя неразличимые участки. Если множеств 2-3, то рисуют круги, если больше 4 – эллипсы. Этот «цветок» помещают в прямоугольную конструкцию, которую называют универсум U (универсальное множество).
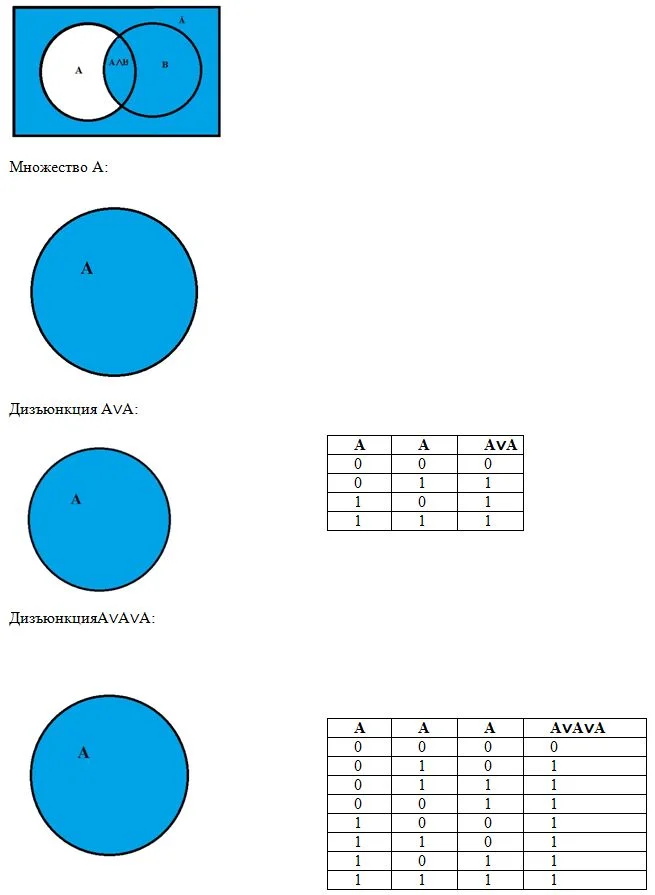
Диаграммы позволяют наглядно увидеть результат большинства логических функций:
Конъюнкция множеств А и В:

Отрицание Ā:
Сложное выражение (Ā)∨(A∧B), составленное из элементарных Ā, A∧B и их комбинации, графическое выражение:
Примеры использования диаграмм Эйлера-Венна
Пример №1:
Есть 2 множества цифр и универсум:
А={4,5,6,7}
В={6,7,8,9}
U={0,4,5,6,7,8,9}
Пустой области ничего не принадлежит, опишем в табличном виде, какие цифры какой области принадлежит:

Логические элементы

Логические операции – основа цифровой техники. Даже цифровые микросхемы, которые предназначены только для выполнения логических операций, называют – «логические микросхемы», или еще проще – «логика».
Немного остановимся на микросхемах логики и мы.
Работа цифровых микросхем логики основана на выполнение трех основных логических операций, с которыми мы ознакомились выше. Сочетание этих логических операций позволило создать большое количество цифровых микросхем логики.Основа таких микросхем – логический элемент.
Логический элемент выполняющий операцию «Логическое И»

Логический элемент выполняющий операцию «Логическое ИЛИ»

Логический элемент выполняющий операцию «Логическое НЕ»

Логический элемент выполняющий операцию «Исключающее ИЛИ»
Логический элемент выполняющий операцию «Логическое ИЛИ-НЕ»
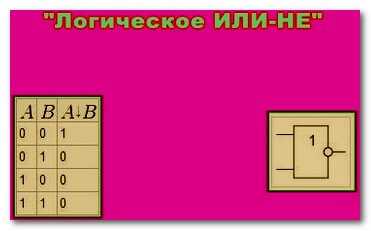
Логический элемент выполняющий операцию «Логическое И-НЕ»

Кроме таких комбинаций логических операций существует еще ряд других.
Кстати, есть еще одна разновидность логики – женская логика. Весьма интересная штука. Но так как она к сегодняшней теме не относится, то придется, к сожалению, этот вопрос опустить.

Предыдущие статьи:1. Микроконтроллеры — первый шаг2. Системы счисления: десятичная, двоичная и шестнадцатиричнаяСледующие статьи:1. Битовые операции2. Прямой, обратный и дополнительный коды двоичного числа
Логические операции и выражения, таблица истинностиЛогика, логические выражения, логические операции, таблица истинности, логические элементы
Published by: Мир микроконтроллеров
Date Published: 02/07/2015




























