Ориентированный граф

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

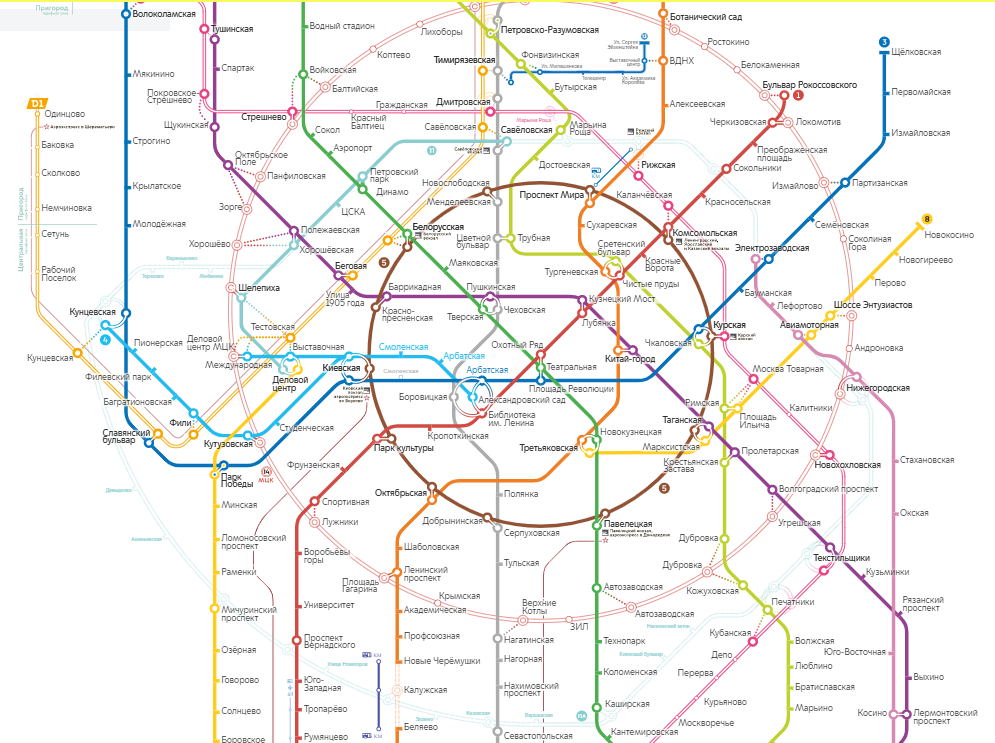Схема Московского метро

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

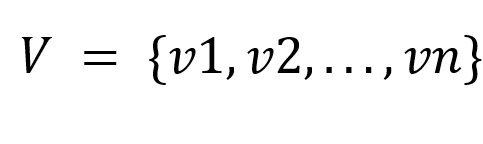
Число рёбер обозначается буквой m:

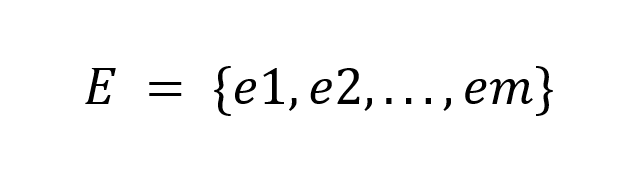
Таким образом граф задается и обозначается парой V,E:

Граф — это совокупность пары множеств. Конечного есть и бесконечные, однако мы их пока не рассматриваем непустого множества V и множества E заданного неупорядоченными парами множества V.

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий

Линии в котором задаются парой вершин, расположенных не важно в каком порядке

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Нулевой граф

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Пример: Пусть множество V = {1,2,3,4,5}. Тогда множество E = {1,2, 2,3, 3,4, 1,5, 1,4, 3,1}

Граф будет выглядеть следующим образом:

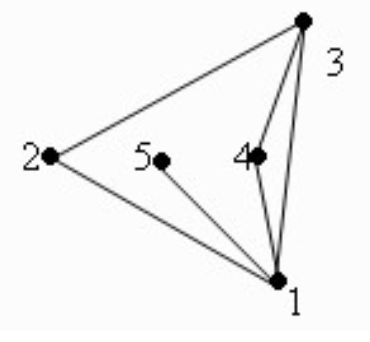
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степенью вершины — является количество рёбер исходящих выходящих из вершины и входящих в нее. Данное определение верно для ориентированных графов см. классификацию графов. Для неориентированных графов исходящая степень равна входящей. Степенью вершины 1 будет является число 4. Так как вершина 1 соединена с вершиной 2, 3, 4, 5.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Минимальную как:

Формула суммы степеней для G = V,E выглядит так:

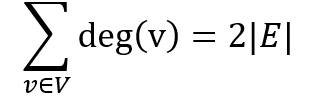
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

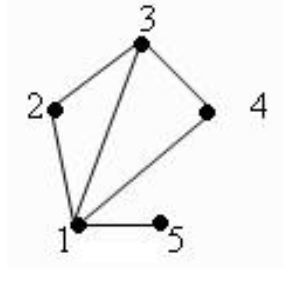
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Самое главное в графе это вершины и проведенные между ними рёбра. В связи с этим граф является топологическим объектом, а не геометрическим . То есть объектом который не меняется при любых растяжениях и сжатиях. Нам все равно какой мы сделали отрезок. Кривой, прямой, самое главное это наличие связи между вершинами. По этой причине графы являются очень универсальными в плане практического применения. Мы можем обозначать ими дороги, компьютерную сеть, людей которые дружат друг с другом или даже влюблены друг в друга.

Введение

Теория графов — раздел дискретной математики, изучающий свойства графов. Она применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электроника, машиностроение, архитектура, исследование операций, генетика, психология, социология, экономика, антропология и лингвистика. При этом обычно на графе решаются задачи о достижимости, задачи сетевого планирования, потоковая задача.

Интерес к проблемам теории графов был сосредоточен главным образом в Англии. Имелось много причин для такого оживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов

Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса

Изучение теории графов является актуальным, так как настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии. Вследствие этого развития предмет теории графов является уже обширным.

Основную проблему в применении теоретико-графовых методов составляет проблема терминологии, так как она далеко не устоялась.

Целью данной работы является подробное рассмотрение теории графов в информатике, выявление их сущности, изучение терминологии, а также способы представления графов в ЭВМ.

Основы и определения

Теория графов основные понятия и определения начала формулировать в XVIII веке. Именно тогда великий математик Леонард Эйлер сумел решить первую в историю задачу о кенигсбергских мостах. Теория систематически и последовательно ведет изучение свойств графов. Они имеют в составе множество точек и линий.

Основы теории графов всегда начинают с рассмотрения математических определений. Первое из них говорит о том, что они есть система вершин и ребер, которые соединяют объекты.

Во втором рассматривается случай, где V есть множество вершин, а v — вершины.

Граф типа G=G (V) с множеством вершин представляет собой некоторое семейство пар e=(a, b).

Указанные точки являются свидетельством того, какие из вершин считают соединенными. Каждая из пар является графовым ребром.

Далее, необходимо рассмотреть основные определения согласно представлениям дискретной математики:

• Смежными называют те вершины, которые имеют соединение в виде ребер.
• Соединяемые этим способом вершины являются инцидентными по отношению к ребру.
• Число инцидентных ребер указывает на вершинную степень.
• В простом графе двойное число ребер равняется степенной сумме.
• Для простого элемента странный парадокс: четное количество вершин равно нечетной степени.

Основные определения

Формальное определение:

Графом \(G\) называется пара множеств \(G = (V, E\), где \(V(G)\) — непустое конечное множество элементов, называемых вершинами графа, а \(E\) — множество пар элементов из \(V\) (необязательно различных), называемых ребрами графа. \(E = \{(u , v)\ | u, v \in V\}\) — множество ребер графа \(G\), состоящее из пар вершин \((u, v)\). Ребро \((u, v)\) соединяет вершины \(u\) и \(v\).

Простое определение:

Граф — это набор вершин (точек) и соединяющих их отрезков (рёбер).

Примеры графа

Две вершины, соединенные ребром, называют смежными вершинами. Обычно в задачах \(N\) — количество вершин, а \(M\) — ребер. Количество ребер, исходящее из вершины называют степенью вершины \(d(v)\). Для вершины \(a\) ребро \((a, b)\) называется инцидентным ей. На рисунке ниже вершине 8 инцидентно только ребро (4, 8), а вершине 10 ребра (2, 10) и (5, 10).

Теоретическое задание

Назовите степень 1-ой и 6-ой вершины и какие ребра инциденты им.

1

Если какие-то две вершины соединены более, чем одним ребром, то говорят, что граф содержит кратные ребра. Если ребро соединяет вершину саму с собой, то такое ребро называют петлей.

Простой граф не содержит петель и кратных ребер. Если не сказано ничего про наличие петель и кратных ребер, мы будем всегда считать, что граф простой.

Теоретическое задание

Сколько может быть рёбер в простом графе в \(N\) вершинами?

2

Теоретическое задание

Найдите цикл размера 4 и петлю в этом непростом графе.

Также часто рассматривают ориентированные графы — это графы, у которых ребра имеют направление, а иначе граф – неориентированный.

Что такое теория графов и что такое граф?

Теория графов — один из обширнейших разделов дискретной математики, широко применяется
в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических
цепей, коммуникации, психологии, психологии, социологии, лингвистике, других областях знаний. Теория графов систематически
и последовательно изучает свойства графов, о которых можно сказать, что они состоят из множеств точек и
множеств линий, отображающих связи между этими точками. Основателем теории графов считается Леонард
Эйлер (1707-1882), решивший в 1736 году известную в то время задачу о кёнигсбергских мостах.

Графы строят для того, чтобы отобразить отношения на множествах.
Пусть, например, множество —
множество людей, а каждый элемент будет отображён в виде точки

Множество —
множество связок (прямых, дуг, отрезков — пока не важно). На множестве A задано отношение
знакомства между людьми из этого множества

Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Естественно, число знакомых у одних людей может отличаться от числа знакомых у других людей, а некоторые
вполне могут и не быть ни с кем знакомы (такие элементы будут точками, не соединёнными ни с одной другой). Вот и получился граф!

То, что мы сначала назвали «точками», следует называть вершинами графа, а то, что
называли «связками» — рёбрами графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует
большое количество самых разных конкретных задач, при решении которых можно временно забыть о специфическом
содержании множеств и их элементов

Эта специфика никак не сказывается на ходе решения задачи, независимо
от её трудности! Например, при решении вопроса о том, можно ли из точки a добраться до
точки e, двигаясь только по соединяющим точки линиям, неважно, имеем ли мы дело с людьми,
городами, числами и т.д. Но, когда задача решена, мы получаем решение, верное для любого содержания,
которое было смоделировано в виде графа

Не удивительно поэтому, что теория графов — один из самых
востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может
обсудить с собеседником и вопросы любви, и вопросы музыки или спорта, и вопросы решения различных задач,
причем делает это без всякого перехода (переключения), без которого в подобных случаях не обойтись человеку.

А теперь строгие математические определения графа.

Определение 1. Графом называется система объектов произвольной
природы (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов.

Определение 2. Пусть – (непустое) множество вершин, элементы – вершины.
Граф с множеством вершин есть некоторое
cемейство пар вида: , где , указывающих,
какие вершины остаются соединёнными. Каждая пара — ребро графа.
Множество — множество рёбер графа. Вершины и – концевые точки ребра .

Графы как структура данных. Широким применением теории графов в
компьютерных науках и информационных технологиях обусловлено добавлением к вышеизложенным определениям
понятия графа как структуры данных. В компьютерных науках и информационных технологиях граф определяется
как нелинейная структура данных. Что же тогда — линейная структура данных и чем от них отличаются графы?
Линейные структуры данных характеризуются тем, что связывают элементы отношениями типа «простого соседства».
Линейными структурами данных являются, например, массивы, таблицы, списки, очереди, стеки, строки. В
противоположность им нелинейные структуры данных — такие, в которых элементы располагаются на различных
уровнях иерархии и подразделяются на три вида: исходные, порождённые и подобные. Итак, граф — нелинейная
структура данных.

Слово граф греческого происхождения, от слов «пишу», «описываю». Из начала этой статьи
известно, что именно описывает граф: описывает он отношения. То есть, любой граф описывает отношения. И
наоборот: любое отношение можно описать в виде графа.

Методы исследования в теории графов

Пре­ж­де все­го вы­де­ля­ют­ся ком­би­на­тор­ные ме­то­ды тео­ре­ти­ко-мно­же­ст­вен­но­го ана­ли­за за­дан­но­го би­нар­но­го от­ноше­ния на мно­же­ст­ве вер­шин. Весь­ма су­ще­ст­вен­ны (осо­бен­но в пе­ре­чис­ли­тель­ных за­да­чах) ал­геб­ра­ические ме­то­ды, в пер­вую оче­редь ме­то­ды тео­рии групп (в ча­ст­но­сти, групп под­ста­но­вок). При изу­че­нии ук­ла­док гра­фа на плос­кость при­вле­ка­ют­ся ре­зуль­та­ты то­по­ло­гич. ха­рак­те­ра. Слу­чай­ные гра­фы изу­ча­ют­ся с по­мо­щью тео­ре­ти­ко-ве­ро­ят­но­ст­ных ме­то­дов.

Осо­бую роль при изу­че­нии гра­фов иг­ра­ют мат­рич­ные ме­то­ды. Для гра­фа $G$ мат­ри­цей смеж­но­сти $A=A(G)=||a_{ij}||$ назы­ва­ет­ся мат­ри­ца, в ко­то­рой $a_{ij}=1$, ес­ли в гра­фе $G$ вер­ши­на $i$ свя­за­на с вер­ши­ной $j$ реб­ром (или ду­гой в ори­ен­ти­ро­ван­ном гра­фе) и $a_{ij}=0$ в про­тив­ном слу­чае. В пер­вом слу­чае го­во­рят, что вер­ши­ны $i$ и $j$ смеж­ны, во вто­ром слу­чае – что они не­смеж­ны. Мар­шру­том в гра­фе $G$ на­зы­ва­ет­ся по­сле­до­ва­тель­ность $v_0e_1v_1…v_{n–1}e_nv_n$, со­стоя­щая по­пе­ре­менно из вер­шин и рё­бер гра­фа, в ко­то­рой реб­ро $e_i$ со­еди­ня­ет вер­ши­ны $v_{i–1}$ и $v_i, i=1, …, n$; го­во­рят, что этот мар­шрут свя­зы­ва­ет вер­ши­ны $v_0$ и $v_n$. Мар­шрут, в ко­то­ром $v_0=v_n$, на­зы­ва­ет­ся цик­лом. Мар­шрут на­зы­ва­ет­ся це­пью (со­от­вет­ст­вен­но, про­стой це­пью), ес­ли все его рёб­ра (все его вер­ши­ны) раз­лич­ны. При $n⩾1$ эле­мент на мес­те $(i, j)$ в мат­ри­це $A^n$ ра­вен чис­лу мар­шру­тов дли­ны $n$ из вер­ши­ны $v_i$ в вер­ши­ну $v_j$. Граф на­зы­ва­ет­ся связ­ным, ес­ли для лю­бых его двух вер­шин су­ще­ству­ет мар­шрут, свя­зы­ваю­щий эти вер­ши­ны. Для гра­фа $G$ с $p$ вер­ши­на­ми и $q$ рёб­ра­ми, в ко­то­ром за­ну­ме­ро­ва­ны как вер­ши­ны, так и рёб­ра, рас­смат­ри­ва­ет­ся мат­ри­ца ин­ци­дент­но­сти $B(G)$, пред­став­ляю­щая со­бой мат­ри­цу, со­стоя­щую из ну­лей и еди­ниц с дву­мя еди­ни­ца­ми в ка­ж­дом столб­це; в столб­це, со­от­вет­ст­вую­щем реб­ру, со­еди­няю­ще­му вер­ши­ны $i$ и $j$, еди­ни­ца сто­ит в стро­ках с но­ме­ра­ми $i$ и $j$. Го­во­рят, что ка­ж­дая из вер­шин $i$ и $j$ и со­еди­няю­щее их реб­ро ин­ци­дент­ны, два реб­ра смеж­ны, ес­ли они име­ют об­щую ин­ци­дент­ную им вер­ши­ну. Ранг мат­ри­цы ин­ци­дент­но­сти $B(G)$ ра­вен $p-1$, ес­ли граф $G$ яв­ля­ет­ся связ­ным гра­фом.

Мно­же­ст­во собств. зна­че­ний мат­ри­цы смеж­но­сти гра­фа или ори­ен­ти­ро­ван­но­го гра­фа (при этом ка­ж­дое зна­че­ние бе­рёт­ся столь­ко раз, ка­ко­ва его крат­ность) на­зы­ва­ет­ся спек­тром гра­фа. Спектр гра­фа с $n$ вер­ши­на­ми со­сто­ит из $n$ дей­ст­ви­тель­ных чи­сел. Изу­че­ние спек­тра гра­фа по­зво­ля­ет вы­яс­нить мн. осо­бен­но­сти его строе­ния.

Классические задачи теории графов и их решения

Один из первых опубликованных примеров работ по теории графов и применения графов — работа о «задаче с
Кёнигсбергскими мостами» (1736 г.), автором которой является выдающийся математик 18-го века Леонард Эйлер.
В задаче даны река, острова, которые омываются этой рекой, и несколько мостов. Вопрос задачи:
возможно ли, выйдя из некоторого пункта, пройти каждый мост только по одному разу и вернуться в
начальный пункт? (рисунок ниже)

Задачу можно смоделировать следующим образом: к каждому участку суши прикрепляется
одна точка, а две точки соединяются линией тогда и только тогда, когда соответствующие участки суши
соединены мостом (рисунок ниже, соединительные линии начерчены пунктиром). Таким образом, построен граф.

Ответ Эйлера на вопрос задачи состоит в следующем. Если бы у этой задачи было
положительное решение, то в получившемся графе существовал бы замкнутый путь, проходящий по рёбрам и
содержащий каждое ребро только один раз. Если существует такой путь, то у каждой вершины должно быть
только чётное число рёбер. Но в получившемся графе есть вершины, у которых нечётное число рёбер.
Поэтому задача не имеет положительного решения.

По устоявшейся традиции эйлеровым графом называется граф, в котором можно обойти все
вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное
число рёбер. Задача средней трудности на эйлеровы графы — в материале «Основные виды графов».

В 1847 г. Кирхгоф разработал теорию деревьев для решения совместной системы линейных
алгебраических уравнений, позволяющую найти значение силы тока в каждом проводнике (дуге) и в каждом
контуре электрической цепи. Абстрагируясь от электрических схем и цепей, которые содержат сопротивления,
конденсаторы, индуктивности и т.д., он рассматривал соответствующие комбинаторные структуры, содержащие
только вершины и связи (рёбра или дуги), причём для связей не нужно учитывать, каким типам электрических
элементов они соответствуют. Таким образом, Кирхгоф заменил каждую электрическую цепь соответствующим
графом и показал, что для решения системы уравнений необязательно рассматривать в отдельности каждый
цикл графа электрической цепи.

Кэли в 1858 г., занимаясь чисто практическими задачами органической химии, открыл
важный класс графов, называемых деревьями. Он стремился перечислить изомеры насыщенных углеводородов,
с данным числом атомов углерода. Кэли прежде всего сформулировал задачу абстрактно: найти число
всех деревьев с p вершинами, каждое из которых имеет вершины со степенями 1 и 4. Ему не удалось
сразу решить эту задачу, и он стал изменять её формулировку таким образом, чтобы можно было решить
новую задачу о перечислении:

• корневых деревьев (в которых выделена одна из вершин);
• всех деревьев;
• деревьев, у которых степени вершин не превышают 4;
• деревьев, у которых степени вершин равны 1 и 4 (постановка задачи из химии).

Часто используемые графы

Определение:

Полный граф (англ. complete graph, clique) — граф, в котором каждая пара различных вершин смежна. Полный граф с вершинами имеет рёбер и обозначается .

Определение:

Двудольный граф или биграф (англ. bipartite graph) — граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части. Двудольный граф с вершинами в одной доле и во второй обозначается .

Определение:

Регулярный граф (англ. regular graph) — граф, степени всех вершин которого равны, то есть каждая вершина имеет одинаковое количество соседей. Регулярный граф с вершинами степени называется ‑регулярным, или регулярным графом степени .

Основная статья: Дерево, эквивалентные определения

Определение:

Дерево (англ. tree) — связный ациклический граф.

Основная статья: Эйлеров цикл, Эйлеров путь, Эйлеровы графы, Эйлеровость орграфов

Определение:

Граф называется эйлеровым (англ. eulerian graph), если он содержит эйлеров цикл.

Основная статья: Гамильтоновы графы

Определение:

Граф называется гамильтоновым (англ. hamiltonian graph), если он содержит гамильтонов цикл.

Основная статья: Укладка графа на плоскости

Определение:

Граф называется планарным (англ. planar graph), если он обладает укладкой на плоскости. Плоским (англ. plane graph, planar embedding of the graph) называется граф уже уложенный на плоскости.

Основная статья: Лемма о безопасном ребре

Определение:

Остовное дерево (англ. spanning tree) — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины.

Базовые понятия теории графов

Определения

Определение:Граф G —это пара множеств $G=(V,E)$, где $V(G)$ — непустое конечное множество элементов, называемых вершинами графа, а $E$ — множество пар элементов из $V$ (необязательно различных), называемых ребрами графа. $E={(u,v) : u,v\in V }$ — множество ребер графа $G$, состоящее из пар вершин $(u,v)$. Ребро $(u,v)$ соединяет вершины $u$ и $v$.

Неформально это можно понимать как набор вершин (точек) и соединяющих их отрезков (рёбер).

Определение:Смежные вершины —это вершины, соединенны ребром

Определение:Степень вершины $d(v)$ —это количество ребер, исходящих из вершины $v$

Определение:Инцидентность —это для ребра $(a,b)$ вершины $a$ и $b$ называются инцидентными. И наоборот, для вершины $a$ любое ребро $(a, x)$ (или $(x, a)$) называется инцидентным данной вершине $a$.

Замечание: две вершины, соединенные ребром, называются именно смежными, инцидентными их назвать нельзя.

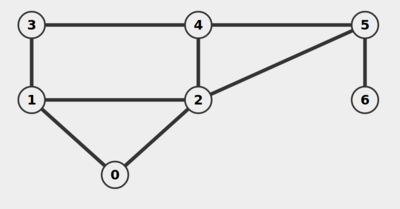
Пример графа

Например, в графе на рисунке степень вершины $2$ равна $4$, вершины $4$ и $5$ смежны. Всего в графе $7$ вершин и $9$ ребер, то есть $|V| = 7$ и $|E| = 9$.

Определение:Кратные ребра —это ребра, которые соединяют одну и ту же пару вершин. Если две вершины соединены более чем одним ребром, говорят, что граф содержит кратные ребра.

Определение:Петля —это ребро, которое соединяет вершину саму с собой

Определение:Простой граф —это граф, который не содержит петель и кратных ребер.

Если не сказано ничего про наличие петель и кратных ребер, мы будем всегда считать, что граф простой.

Определение:Взвешенный граф —это граф, каждому ребру которого присвоено некоторое вещественное число, называемое весом ребра. Иными словами, на множестве ребер задана функция $W : E \rightarrow \mathbb{R}$.

Определение:Ориентированный граф —это граф, в котором каждое ребро имеет направление, то есть ребро уже не просто соединяет две вершины, а в этой паре выбрано начало и конец ребра.

На рисунке изображен неориентированный граф. Его легко сделать ориентированным, если задать направление для каждого ребра. В некоторых задачах бывает удобно рассматривать неориентированный граф как ориентированный, но в котором у каждого ориентированного ребра $(u, v)$ (ведет из $u$ в $v$) есть парное ребро $(v, u)$. Получаем, что по ребру можно перемещаться в обе стороны, то есть граф неориентированный.

Определение:Связный граф —это граф, в котором из любой вершины можно по ребрам дойти до любой другой. Относится только к неориентированным графам.

Виды графов

Приведенные множества графов пересекаются.

• Дерево — связный граф без циклов;
• Планарный граф — граф, который можно разложить на плоскости так, чтобы его ребра не пересекались в точках, отличных от вершин;
• Полный граф — граф, в котором каждая вершина соединена с каждой;
• Двудольный граф — граф, вершины которого можно разделить на два множества таких, что ребра соединяют только вершины из разных множеств.

Что такое граф и из чего состоит информатика

Информатика — это наука о преобразовании, хранении и передаче информации с помощью компьютеров. Она изучает принципы и методы обработки данных, а также разработку и использование компьютерных систем.

Основные элементы информатики включают в себя алгоритмы, структуры данных, программирование, базы данных, компьютерные сети и искусственный интеллект. Алгоритмы — это последовательность инструкций, которые определяют, как решить конкретную задачу. Структуры данных — это способ организации и хранения данных для эффективного доступа и обработки. Программирование — это процесс создания программного обеспечения с использованием определенного языка программирования. Базы данных — это средства хранения и организации больших объемов данных. Компьютерные сети — это системы связи, которые позволяют компьютерам обмениваться информацией. Искусственный интеллект — это область, которая изучает разработку компьютерных систем, способных к обучению, принятию решений и выполнению задач, требующих интеллектуальных способностей.