Содержание
А следствие это результат, широко используемый в геометрии для обозначения немедленного результата чего-то уже доказанного. Следствия обычно появляются в геометрии после доказательства теоремы.
Поскольку они являются прямым результатом доказанной теоремы или известного определения, следствия не требуют доказательства. Эти результаты очень легко проверить, поэтому их доказательство опускается.

Следствия — это термины, которые в основном встречаются в области математики. Но это не ограничивается использованием только в области геометрии.
Слово следствие происходит от латинского венчик, и обычно используется в математике, особенно в областях логики и геометрии.
Когда автор использует следствие, он говорит, что этот результат может быть обнаружен или выведен самим читателем, используя в качестве инструмента некоторую ранее объясненную теорему или определение.
16.4. Аксиомы и теоремы в геометрии window.top.document.title = «16.4. Аксиомы и теоремы в геометрии»;
Как было отмечено ранее, изучение геометрии основано на аксиоматическом методе. После формулировки основных понятий и аксиом все дальнейшие результаты теории – результаты логических рассуждений, которые оформляются в виде определенного вида утверждений. Рассмотрим это более подробно.
Теорема – утверждение, требующее доказательства. Таковыми являются, например, теоремы 1.1 и 1.2.
Лемма – вспомогательная теорема, которая приводится для того, чтобы с ее помощью доказать следующую теорему или группу теорем. Например, с помощью леммы 1.1 мы доказали теорему 1.2.
Следствие (из определения, теоремы, аксиомы) – теорема, которая позволяет более полно трактовать содержание данной теоремы, аксиомы, определения. Например, следствие 1.1 раскрывает дополнительные свойства двух прямых на основании аксиомы 1.2; следствие 1.2 – свойства точек, принадлежащих разным полуплоскостям, следующие непосредственно из определения 1.9 и аксиомы 1.6. Таким образом, основным средством познания (выяснения новых свойств геометрических фигур) в геометрии является доказательство теорем.
Рассмотрим, например, формулировку теоремы, данную в следствии 1.1: если на луче отложить от начальной его точки два отрезка AB и AC и если AB = AC, то точки B и C совпадут. Условием теоремы является предложение {на луче отложить от начальной его точки два отрезка AB и AC и AB = AC}. Это предложение не является в данном виде высказыванием, но содержит описание множества объектов, относительно которых делается высказывание вида AB = AC. Из описания ясно, что речь идет о множестве отрезков луча a, отложенных от начальной его точки. Поскольку один конец отрезка фиксирован, то отрезок определяется однозначно точкой луча. Обозначим как P множество точек луча, отличных от его начальной точки. Пусть B P – заданная точка. Тогда условие теоремы является предложением относительно точки множества P. Перепишем условие теоремы в виде: A (x) = {длина отрезка Ax = AB}. Очевидно, это предикат. Заключение теоремы есть предикат B (x) = {точка x совпадает с точкой B}. Тогда теорему можно переформулировать следующим образом: если x – произвольная точка луча AB такая, что Ax = AB, тогда точка x совпадает с точкой B, которую можно записать в виде
Утверждается, что любую теорему можно записать в таком виде (мы показали на данном примере, как это можно сделать в частном случае), поэтому проанализируем структуру теоремы.В ней можно выделить три части:
- Условие теоремы: предикат A (x), заданный на множестве точек луча AB, без его начальной точки.
- Заключение теоремы: предикат B (x), заданный на множестве точек луча AB за исключением точки A.
- Разъяснительная часть: в ней описывается множество объектов, о которых идет речь в теореме.
В символической записи теоремы к разъяснительной части теоремы следует отнести запись
Пусть – запись истинной теоремы. Тогда ее условие и заключение образуют импликацию, истинную при всех x из множества X, и, следовательно, предикат B (x) логически следует из предиката A (x). Поэтому заключение теоремы B (x) является необходимым условием для условия A (x), а условие A (x) – достаточным для заключения теоремы B (x).
Определение 16.30.
Пусть A (x) и B (x) – два предиката, заданные на множестве X. Тогда теоремы и называются обратными друг к другу.
Определение 16.31.
Если истинны обе теоремы и то говорят, что каждый из предикатов A (x) и B (x) является необходимым и достаточным условием другого. Обе теоремы при этом можно объединить в одну теорему вида
Пусть дана теорема
Определение 16.32.
Теорема называется противоположной к данной.
Определение 16.33.
Теорему называют теоремой, противоположной обратной.
Теорема 16.1.
Теорема равносильна противоположной обратной.
На основании этого утверждения основан метод доказательства от противного. Суть этого метода состоит в том, что доказывают истинность теоремы, противоположной обратной, поскольку если эта теорема истинна, то и исходная теорема тоже верна.
| Сайт знакомств: чат рулетка с девушками 18 . Видеочат онлайн. |
| virtruletka18.ru |
Советы по использованию следствий
Следствия в геометрии являются важным инструментом для решения задач и доказательства теорем. Ниже приведены несколько полезных советов по использованию следствий:
Ознакомьтесь с основными следствиями: перед тем, как начать решать задачу или доказывать теорему, изучите основные следствия, которые могут быть полезны в данной ситуации
Это поможет вам быстрее и эффективнее приступить к решению.
Используйте подобие и равенство: если в задаче или теореме есть подобные фигуры или равные отрезки и углы, обратите на это внимание. Знание основных следствий о подобии и равенстве позволит вам легче решить задачу или доказать теорему.
Пользуйтесь свойствами параллельных и пересекающихся прямых: следствия о параллельных и пересекающихся прямых могут быть полезны при решении задач на построение или доказательство утверждений о прямых и углах.
Используйте свойства треугольников: запомните основные следствия о треугольниках, такие как теорема о сумме углов треугольника, теоремы о равенстве треугольников и пропорциональности сторон треугольников
Это поможет вам решить задачи и доказать теоремы, связанные с треугольниками.
Обращайте внимание на множественность следствий: одно и то же следствие может быть использовано для решения различных задач и доказательства разных теорем. Поэтому, изучив следствие, старайтесь применять его в разных ситуациях.
Помните, что использование следствий требует практики. Чем больше вы будете решать задачи и доказывать теоремы, тем лучше вы освоите использование следствий и станете более уверенными в решении геометрических задач.
Основные понятия геометрии
В геометрии существуют основные понятия, которые необходимо знать и понимать, чтобы успешно работать с фигурами и проводить логические рассуждения. Некоторые из этих понятий включают:
1. Точка: самый простой элемент геометрии, который не имеет размеров, но имеет позицию в пространстве. Обозначается заглавной буквой.
2. Линия: множество точек, протяженность которых бесконечна в обоих направлениях. По линии можно провести прямую, дугу или отрезок.
3. Отрезок: часть прямой, обозначаемая двумя ее концевыми точками. Имеет определенную длину.
4. Прямая: линия, которая не имеет ни начала, ни конца. Она продолжается бесконечно в обоих направлениях.
5. Плоскость: геометрическая фигура, которая распространяется в двумерном пространстве. Она не имеет толщины, но имеет длину и ширину.
6. Угол: область плоскости, образованная двумя лучами, которые имеют одну общую начальную точку, называемую вершиной угла.
7. Треугольник: фигура, состоящая из трех отрезков (сторон) и трех точек (вершин).
8. Четырехугольник: фигура, состоящая из четырех отрезков (сторон) и четырех точек (вершин).
Это лишь некоторые из основных понятий геометрии, которые необходимо понимать, чтобы успешно изучать и применять ее принципы. Углубляясь в изучение геометрии, вы будете знакомиться со множеством других понятий и закономерностей, которые позволят вам решать сложные задачи и проводить доказательства.
Правило встречается в следующих упражнениях:
1 класс
Страница 41,Моро, Волкова, Степанова, Учебник, часть 1
Страница 84,Моро, Волкова, Степанова, Учебник, часть 2
Страница 13,Моро, Волкова, Рабочая тетрадь, часть 2
Страница 1. Урок 1,Петерсон, Учебник, часть 1
Страница 5. Урок 3,Петерсон, Учебник, часть 1
Страница 7. Урок 4,Петерсон, Учебник, часть 1
Страница 9. Урок 5,Петерсон, Учебник, часть 1
Страница 21. Урок 13,Петерсон, Учебник, часть 1
Страница 23. Урок 14,Петерсон, Учебник, часть 1
Страница 60. Урок 37,Петерсон, Учебник, часть 1
2 класс
Страница 28,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 92,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72. Урок 37,Петерсон, Учебник, часть 1
Страница 73. Урок 37,Петерсон, Учебник, часть 1
Страница 20. Урок 6,Петерсон, Учебник, часть 2
Страница 24. Урок 8,Петерсон, Учебник, часть 2
Страница 97. Урок 40,Петерсон, Учебник, часть 2
Страница 30. Урок 10,Петерсон, Учебник, часть 3
Страница 83. Урок 32,Петерсон, Учебник, часть 3
3 класс
Страница 15,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29. Урок 10,Петерсон, Учебник, часть 1
Страница 35. Урок 13,Петерсон, Учебник, часть 1
Страница 67. Урок 22,Петерсон, Учебник, часть 1
Страница 79. Урок 28,Петерсон, Учебник, часть 1
Страница 85. Урок 31,Петерсон, Учебник, часть 1
Страница 29. Урок 12,Петерсон, Учебник, часть 2
Страница 48. Урок 19,Петерсон, Учебник, часть 2
Страница 50. Урок 20,Петерсон, Учебник, часть 2
Страница 70. Урок 29,Петерсон, Учебник, часть 2
4 класс
Страница 57,Моро, Волкова, Рабочая тетрадь, часть 1
Страница 30,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы
Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам
Способы доказательства геометрических теорем
- Синтетический или синтез — метод, при котором данное предложение выступает, как необходимое следствие другого, уже доказанного.
- Аналитический или анализ — обратный синтезу способ. Рассуждения всегда начинаются с доказываемой теоремы и закачиваются другой известной истиной.
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
- Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.
- Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
- Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
- прямая теорема: в треугольнике против равных сторон лежат равные углы.
- обратная теорема: в треугольнике против равных углов лежат равные стороны.
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
- Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
- Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
- Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
- Обратная противоположной: если прямые не параллельны, соответственные углы не равны.
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Следствия из аксиомы параллельности: первое следствие
Проведем две прямые $a$ и $b$ таким образом, чтобы каждая была параллельна третьей прямой $c$. Докажем, что $a$ и $b$ параллельны между собой, то есть что если $a\parallel{c}$ и вместе с тем $b\parallel{c},$ то $a\parallel{b}$.
Доказательство
Пойдем от противного и предположим, что $a$ и $b$ не параллельны. Тогда они должны пересекаться в некоторой точке.
Если бы это действительно было так, то через точку пересечения можно было бы провести две прямые, параллельные $c,$ — напомним, по условию $a\parallel{c}$ и $b\parallel{c}$. Это противоречит аксиоме параллельности, ведь через одну точку невозможно провести две параллельные прямые. Значит, $a\parallel{b}$. Следствие доказано.
Алгоритм доказательства следующий: вначале вводится утверждение от противного, чтобы после привести его к противоречию с аксиомой, теоремой или определением. Если в ходе доказательства противоречия не обнаруживается — следствие ошибочно. Это стандартная процедура «обратного» доказательства, она ранее известна нам как доказательство от противного.
{"questions":[{"content":"Проверьте себя. Насколько хорошо вы поняли алгоритм? Дано некоторое утверждение $A$. Восстановите правильный порядок схемы доказательства истинности утверждения методом от противного. В случае сложностей обратитесь к разъяснению ниже. `sorter-1`","widgets":{"sorter-1":{"type":"sorter","items":}}}]}
Доказательство от противного: импликация
Мы вновь возвращаемся к импликациям — они же следствия, они же связка «если одно, то другое». Здесь законы логики просты: из «если»-правды нельзя вывести «то»-ложь и получить истину.
Иными словами, можно сказать, что раз некоторое суждение $A$ истинно, то никак из него нельзя вывести противоречивое, ложное суждение $B$. С толку сбивает, пожалуй, отрицание $A$, но в этом и заключается суть метода: пытаться доказывать не истинность $A$, а истинность $\bar{A}$.
В логике частица «не» — отрицание — обозначается как черточка ($\bar{A}$) или также с помощью инверсионного символа ($\neg{A}$).
Если за правду вы принимаете «суждение от противного» $\bar{A}$, то есть отрицание $A$, из этого суждения выводите ложное следствие $B$, то $\bar{A}$ — ложь. Вывод понятный, ведь, повторимся, из правды ложь не выводится. Из чего следует истинность $A$: раз не $\bar{A}$, тогда $A$. Третьего не дано.
Доказательство от противного: задача на логику
Задача. У маляра есть банки только с желтой и фиолетовой красками. Банки с желтой краской всегда большие. Есть маленькая банка с краской. Докажите, что краска в ней фиолетовая.
Давайте покажем формальную схему, как устроено доказательство от противного, на примере простой логической задачи.
$A$ — краска в банке фиолетовая.$\bar{A}$ — краска в банке желтая («не фиолетовая», отрицание $A$).$B$ — банка большая.
Допустим, $\bar{A}$ — истинное суждение: краска в банке-икс не фиолетовая, а желтая. По условию известно, что большой банка может быть, только если краска в ней желтая. Выходит, что «если $\bar{A}$, то $B$». Но это невозможно, поскольку заведомо также известно, что банка-икс маленькая.
Мы обнаружили противоречие, которое сообщает о том, что утверждение $\bar{A}$ в применении к банке-икс ложное. Следовательно утверждение $A$ — истина, что и требовалось доказать. Банка фиолетовая.
О противоречиях
Внимательный читатель мог заметить странность, связанную с противоречиями
Изначально, когда речь шла про следствия, мы подчеркнули важность их доказательства, дабы исключить противоречие с аксиомой-основой или теоремой-основой. Следствие не может противоречить аксиоме, из которой оно выводится, и это факт
Однако при этом мы указывали, что если в ходе доказательства следствия не обнаруживается противоречия, то следствие является ошибочным. Противоречия нет, а следствие ошибочное?
Не забывайте, что речь идет не просто о доказательстве, а о доказательстве от противного. За основу принимается отрицание следствия. При отрицании истинного следствия отсутствие противоречия недопустимо.
Истинное следствие не должно противоречить аксиоме-основе.Отрицание истинного следствия должно противоречить аксиоме-основе.
Помогите пожалуйста ответами на вопрос :1?
Помогите пожалуйста ответами на вопрос :
1.
Многоугольник.
Вывод формулы суммы углов многоугольника.
2. Четырехугольник.
Виды четырехугольников.
Определение и признаки параллелограммов.
Доказать один из признаков параллелограмма.
3. Четырехугольник.
Виды четырехугольников.
Определение и свойства параллелограмма.
Доказать одно из свойств параллелограмма.
4. Определение видов параллелограммов, их свойства.
Доказать одно из свойств.
5. Определение трапеции.
Виды трапеций.
Доказать одно из свойств равнобедренной трапеции.
6. Понятие площадь и ее свойства.
Вывод формулы площади параллелограмма.
7. Понятие площадь и ее свойства.
Формулы площади треугольника.
Вывод одной из формул
площади треугольника.
8. Понятие площадь и ее свойства.
Вывод формулы площади трапеции.
9. Прямоугольный треугольник.
Его свойства.
Вывод теоремы Пифагора.
10. Прямоугольный треугольник.
Его свойства.
Доказательство теоремы, обратной теореме
Пифагора.
11. Определение подобных треугольников.
Признаки подобных треугольников.
Один из
признаков доказать.
12. Определение биссектрисы треугольника.
Доказать свойство биссектрисы треугольника.
13. Определение средней линии треугольника.
Доказать теорему о свойстве средней линии
треугольника.
14. Определение средней линии трапеции.
Доказать теорему о средней линии трапеции.
15. Определение медианы треугольника.
Доказать свойство медиан треугольника.
16. Определение прямоугольного треугольника.
Пропорциональные отрезки в прямоугольном
треугольнике.
17. Определение синуса, косинуса, тангенса острого угла в прямоугольном треугольнике.
Основные тригонометрические формулы.
Значение синуса, косинуса, тангенса для углов 0
,
30
, 45
, 60
, 90
, 180
18. Определение окружности.
Взаимное расположении прямой и окружности.
Доказать
свойство касательной к окружности.
19. Определение центрального угла и угла вписанного в окружность.
Доказательство теоремы
о вписанном угле.
Следствия из этой теоремы.
20. Определение хорды окружности.
Доказательство теоремы об отрезках пересекающихся
хорд.
21. Определение высоты треугольника.
Теорема о точке пересечения высот треугольника.
22. Определение окружности вписанной в многоугольник.
Доказательство теоремы об
окружности, вписанной в треугольник.
23. Определение окружности вписанной в многоугольник.
Доказательство теоремы об
окружности, вписанной в четырехугольник.
24. Определение окружности описанной около многоугольника.
Доказательство теоремы об
окружности, описанной около треугольника.
25. Определение окружности описанной около многоугольника.
Доказательство теоремы об
Аксиомы планиметрии
Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости: треугольники, окружности, параллелограммы и т. д.
Стереометрия (от др.-греч. στερεός — «объёмный, пространственный» + μετρέω — «измеряю») — раздел евклидовой геометрии, в котором изучаются свойства фигур в пространстве: шар, куб, конус и т.д.
Аксиома (др.-греч. ἀξίωμα «утверждение, положение») — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства. Синоним слова: постулат.
Аксиомы планиметрии – система аксиом, в которой собраны утверждения, не требующие доказательств, в отношениях с неопределяемыми (или основными) понятиями в планиметрии (точка, прямая, плоскость).
В «Началах» Евклида была дана система аксиом, на которой базируется вся евклидова геометрия:
- От всякой точки до всякой точки можно провести прямую линию.
- Ограниченную прямую можно непрерывно продолжать по прямой.
- Из всякого центра всяким радиусом может быть описан круг.
- Все прямые углы равны между собой.
- Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.
Эта система была достаточна для того, чтобы один математик понял другого, но в доказательствах неявно использовались и другие интуитивно очевидные утверждения. В 1899 году Гильберт предложил первую достаточно строгую аксиоматику евклидовой геометрии. Система аксиом Гильберта состоит из 20 аксиом и поделена на 5 групп: аксиомы принадлежности, аксиомы порядка, аксиомы конгруэнтности, аксиома параллельности, аксиомы непрерывности.
Существуют и современные системы аксиом, среди которых наиболее известные: аксиоматика Александрова, аксиоматика Биркгофа, аксиоматика Тарского и другие. В российских учебных заведениях изучают, как правило, 10 аксиом, разбитых на 5 групп.
Аксиомы планиметрии, используемые в дисциплинах«Начертательная геометрия» и «Инженерная графика»:
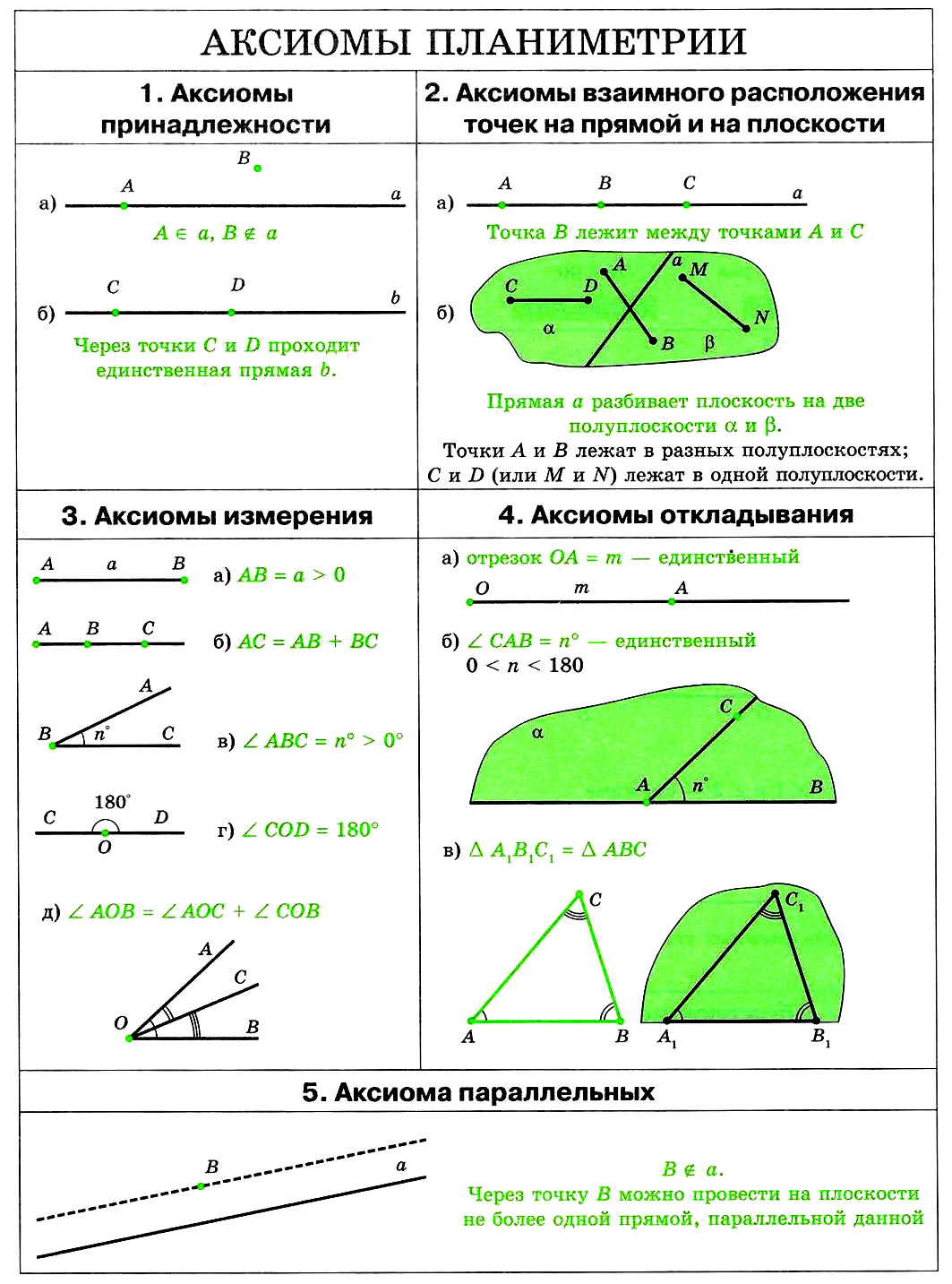
1. Аксиомы принадлежности
1.1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
1.2. Через любые две точки можно провести прямую, и только одну.
2. Аксиомы взаимного расположения точек на прямой и плоскости
2.1. Из трех точек на прямой одна и только одна лежит между двумя другими.
2.2. Прямая разбивает плоскость на две полуплоскости.
3. Аксиомы измерения
3.1. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумму длин частей, на которые он разбивается любой его точкой.
3.2. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4. Аксиомы откладывания
4.1. На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один.
4.2. От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180 градусов, и только один.
4.3. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
5. Аксиома параллельности
5.1. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Это конспект по теме «Аксиомы планиметрии». Выберите дальнейшие действия:
Планиметрия – основные понятия и аксиомы
Представь, что ты вдруг очутился на другой планете, ну или… в компьютерной игре.
Перед тобой набор неизвестных продуктов, а твоя задача – приготовить из этого набора как можно больше вкусных блюд. Что тебе понадобится?
Конечно же, правила, инструкции – что можно делать с теми или иными продуктами. А то вдруг ты сваришь то, что едят только в сыром виде или, наоборот, положишь в салат то, что непременно нужно варить или жарить? Так что, без инструкций – никуда!
Хорошо, но к чему такое вступление? При чем тут геометрия? Понимаешь, великое множество утверждений о всяких фигурах в геометрии и есть то самое множество «блюд», которые мы должны научиться готовить.
Но из чего? Из основных объектов геометрии! А вот инструкция по их «употреблению» называется умными словами «система аксиом».
Применение следствий в прикладных науках
Следствия в математике являются важным инструментом для решения различных задач и задач реального мира. В прикладных науках, таких как физика, экономика, компьютерные науки и инженерия, следствия играют ключевую роль в разработке теорий и моделей.
Одним из применений следствий является обобщение и расширение ранее известных результатов. Следствия позволяют установить связь между различными математическими концепциями и вывести новые утверждения на основе уже существующих. Например, следствие из теоремы Пифагора может быть использовано для выведения формулы для длины гипотенузы треугольника в произвольном пространстве.
Кроме того, следствия используются для доказательства и опровержения гипотез и теорий. В некоторых случаях, следствие может подтвердить или опровергнуть определенную гипотезу или утверждение, что позволяет исследователям лучше понять взаимосвязь между различными переменными или явлениями.
Еще одним применением следствий в прикладных науках является создание практических алгоритмов и моделей. Например, следствие из теории вероятностей может использоваться для разработки алгоритмов прогнозирования рисков или оценки вероятности наступления определенных событий. Такие модели основаны на математических законах и следствиях и помогают принимать решения в условиях неопределенности.
Примеры применения следствий в прикладных науках
Наука
Пример применения следствия
Физика
Следствие из закона сохранения энергии может быть использовано для расчета траектории движения тела в пространстве.
Экономика
Следствие из теории предельной полезности может быть использовано для определения оптимального выбора потребительской корзины.
Компьютерные науки
Следствие из теории графов может быть использовано для разработки алгоритмов поиска кратчайшего пути в сети.
Инженерия
Следствие из электрических цепей может быть использовано для разработки электронных систем управления.
Использование следствий в прикладных науках позволяет повысить качество и достоверность исследований, а также разработать новые методы анализа и решения задач. Без следствий, применение математических концепций и теорий в прикладных науках было бы затруднено и неэффективно.
Основные понятия введения в стереометрию
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.
Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.
Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.
Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.
Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).
Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.
Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).
Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).




























