Алгоритмизация

Лекция 2. Понятие алгоритма и вычислимость функции.

Понятие алгоритма

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, — процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.
Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Вычислимость функции

Функция f с натуральными аргументами и значениями называется вычислимой, если существует алгоритм, ее вычисляющий, то есть такой алгоритм A, что

• если f(n) определено для некоторого натурального n, то алгоритм A останавливается на входе n и печатает f(n) ;
• если f(n) не определено, то алгоритм A не останавливается на входе n.

Несколько замечаний по поводу этого определения:

Понятие вычислимости определяется здесь для частичных функций (областью определения которых является некоторое подмножество натурального ряда). Например, нигде не определенная функция вычислима (в качестве A надо взять программу, которая всегда зацикливается).
Можно было бы изменить определение, сказав так: » если f(n) не определено, то либо алгоритм A не останавливается, либо останавливается, но ничего не печатает «. На самом деле от этого ничего бы не изменилось (вместо того, чтобы останавливаться, ничего не напечатав, алгоритм может зацикливаться).
Входами и выходами алгоритмов могут быть не только натуральные числа, но и двоичные строки (слова в алфавите {0,1} ), пары натуральных чисел, конечные последовательности слов и вообще любые, как говорят, » конструктивные объекты «. Поэтому аналогичным образом можно определить понятие, скажем, вычислимой функции с двумя натуральными аргументами, значениями которой являются рациональные числа. Для функций, скажем, с действительными аргументами и значениями понятие вычислимости требует специального определения. Здесь ситуация сложнее, определения могут быть разными, и мы о вычислимости таких функций говорить не будем. Отметим только, что, например, синус (при разумном определении вычислимости) вычислим, а функция sign(x), равная -1, 0 и 1 при x 0 соответственно — нет. Точно так же требует специального определения вычислимость функций, аргументами которых являются бесконечные последовательности нулей и единиц и т.п.
Несколько десятилетий назад понятие алгоритма требовало специального разъяснения. Сейчас (» компьютерная грамотность «?) такие объяснения все равно никто читать не будет, поскольку и так ясно, что такое алгоритм

Но все же надо соблюдать осторожность, чтобы не принять за алгоритм то, что им не является. Вот пример неверного рассуждения:

» Докажем», что всякая вычислимая функция f с натуральными аргументами и значениями может быть продолжена до всюду определенной вычислимой функции g: N -> N . В самом деле, если f вычисляется алгоритмом A, то следующий алгоритм B вычисляет функцию g, продолжающую f: » если A останавливается на n, то B дает тот же результат, что и A ; если A не останавливается на n, то B дает результат (скажем) 0 «.

История возникновения термина

Сегодня это понятие является фундаментальным и в математике, и в информатике. Однако сам термин возник задолго до появления компьютеров и прочих электронных средств вычислительной техники. Впервые об алгоритме заговорили в средние века — именно тогда европейские ученые ознакомились с методами вычисления арифметических действий, производимых в десятичной системе счисления азиатским математиком по имени Мухаммед ибн Муса аль-Хорезми (от имени этого математика и сформировался термин Algorithm). Сочинение аль-Хорезми перевели, а в последующие столетия появилось много трудов, посвященных вопросу обучения искусству счёта посредством цифр. Можно вспомнить описание алгоритма в европейской науке в те годы:

Также значение слова «алгоритм» сегодня нередко связывают со значениями таких слов, как «рецепт», «метод», «процесс», «инструкция».

Главные характеристики

Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.

Величины

Компьютерная программа
всегда так или иначе использует и обрабатывает данные.
Данные можно ввести в программу в виде
констант, переменных или массивов.
Кроме того каждый вид величин разделяется на типы данных(
числовые, строковые, логические и т.д.).

Константа — величина, которую
компьютер не может изменить в ходе выполнения программы. В
Qbasic константы чаще всего задаются в
явном виде, то есть числовые константы записываются как числа,
строковые — как текст, заключенный в кавычки и т.д. (можно также
задавать константы с помощью имен, в этом случае значения
констант задаются в разделе описаний в начале программы).

Переменная — величина,
значение которой может меняться в ходе выполнения программы.
Переменные задаются с помощью имен. Переменную в
программировании можно понимать как ячейку памяти для временного
хранения информации.

Массив- совокупность однотипных данных,
имеющих общее имя. Массивы позволяют организовать циклы
обработки данных в которых параметр цикла указывает на индекс
элемента массива. Их классифицируют по типу данных (числовые,
строковые, логические) и по размерности (одномерные, двухмерные,
трехмерные и т.д.). Каждый элемент массива представляет собой
переменную величину. Для указания на элемент массива в программе
записывается имя массива и рядом в скобках набор индексов (для
одномерных-1 индекс; для двухмерных -2 (строка, столбец) и
т.д.), например A(17) — 17й по счету
элемент одномерного массива А. Значение, хранящееся в нем, не
связано с его номером.

Способы описания алгоритмов

Существуют различные способы описания алгоритмов. Приведем основные из них:

• словесный (пошаговое описание);
• табличный и в виде формул;
• графический (в виде схем);
• с использованием псевдокода (алгоритмического языка).

Алгоритмический язык является формальным языком, предназначенным для записи алгоритма. В его состав входят набор основных символов (алфавит), система точных правил построения текстов (синтаксис) и система соответствия синтаксически допустимых текстов языка описываемым действиям и объектам (семантика).

Множество языков программирования, используемых при ре¬шении задач на ЭВМ, являются алгоритмическими.

Псевдокод представляет собой способ описания логики программы до начала ее программирования и занимает промежуточное положение между машинным языками и естественными.

Под схемой алгоритма понимают графическое пред¬ставление последовательности шагов алгоритма, наглядно показывающее взаимосвязь опера¬ций, которые осуществляются в алгоритме на каждом шаге, и их очередность. Другими словами, для графического изображения структуры алгоритма используется блок-схема.

В соответствии с блок-схемой последовательность действий указывается с по¬мощью стрелок, которые соединяют отдельные блоки и показывают, какой блок и за каким должен быть выполнен.

Свойства алгоритмов

Существует ряд определенных требований к алгоритмам. Перечислим семь важных свойств, которыми должен обладать каждый алгоритм:

1. Наличие ввода исходных данных.
2. Наличие вывода результата выполнения.
3. Однозначность, так как компьютеру понятны лишь однозначные инструкции.
4. Общность, в соответствии с которой алгоритм может использоваться не только для решения одной задачи, но и целого класса задач.
5. Корректность, согласно которой при выполнении алгоритма должно быть всегда правильное решение задачи.
6. Конечность означает, что решение задачи необходимо получить за конечное число шагов.
7. Эффективность означает, что для решения задачи необходимо использовать ограниченные ресурсы компьютера (объем оперативной памяти, процессорное время и т. д.).

Эффективность алгоритма определяют с учетом потребляемых ресурсов компьютера, к которым относят быстродействие (количество выполняемых операций и затраты трудоемкости на каждую из них) и общий объем оперативной памяти, которая выделяется под данные. Приведенные показатели могут иногда быть противоречивыми: так в результате повышения быстродействия могут потребоваться дополнительные расходы памяти и наоборот. При возможности улучшения одного показателя без ущерба для другого необходимо этого добиваться. В случаях, когда возникает дилемма, рекомендуется предпочесть экономию памяти в ущерб производительности, поскольку тактовая частота процессоров растет опережающими темпами по сравнению с объемами оперативной памяти.

Специалистами предлагается ряд мер для повышения эффективности.

Блок–схемы алгоритма: виды и примеры

Функциональный (операторный) блок:

Его еще называют процессом. Такой элемент нужен для указания действия (шага) алгоритма. Он представляет собой прямоугольник, в который может входить одна направленная линия и выходить тоже одна линия. Внутри записывают команду, подлежащую выполнению. Для наглядности возможна запись нескольких команд в одном блочном элементе.

Альтернативный блок:

Это условный блок, т. к. в нем прописывается какое-нибудь условие. Он указывает наличие выбора среди одного из двух вероятных действий. Геометрическая фигура представляет собой ромб. Внутри прописывается условие выбора (вопрос, сравнение). В качестве условия может выступать выражение, для которого справедливо лишь одно из 2-х значений: «ложь» либо «истина».

В ромб может входить одна направленная линия, а выходить две направленные линии, причем одна подписывается словом «Да», вторая — «Нет». В случае, если записанное внутри геометрической фигуры условие является верным (значение истинно), управление передается по стрелке, которая подписана словом «Да». В обратной ситуации управление переходит на стрелку «Нет».

Блок цикла:

Служит для организации циклического процесса с каким-нибудь параметром. Должно быть известно как число итераций (повторений) цикла, так и шаг изменения параметра. Внутри через запятую прописывается начальное значение циклического параметра, а также шаг изменения и конечное значение.

Блок подпрограммы (предопределенного процесса):

Применяется в целях указания обращения к отдельным модулям, библиотечным подпрограммам, вспомогательным алгоритмам.

Элемент печати:

Обозначает вывод результатов на печать.

Исходя из вышесказанного, пример простейшей блок-схемы алгоритма (речь идет о линейной последовательности) будет выглядеть следующим образом:

Следующий пример представляет собой схематическое описание (блок-схему) итога работы алгоритма целочисленных преобразований с оператором присваивания :=:

Какими бывают алгоритмы

Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.

Линейные. Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.

Ветвящиеся. В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.

Циклические. Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.

Рекурсивные. Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.

Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.

Вероятностные. Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.

Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.

Станьте дата-сайентистом и решайте амбициозные задачи с помощью нейросетей

Подробнее

Информатика и ИКТ

Ключевые слова:

• управление
• алгоритм управления
• обратная связь

3.6.1. Управление

Управление — это процесс целенаправленного воздействия на объект; осуществляется для организации функционирования объекта по заданной программе.

В середине прошлого века выдающийся американский учёный Норберт Винер (1894—1964), изучавший различные технические и биологические системы, установил, что управление в них осуществляется по общей схеме. Винер считается основоположником науки об управлении — кибернетики.

Управляемым объектом (объектом управления) может быть техническое устройство (например, автомобиль), один человек (например, ученик, солдат) или коллектив (например, оркестр, работники предприятия).

Управляющим объектом (управляющей системой) может быть человек (например, шофёр, дирижёр оркестра, учитель, директор), коллектив (например, правительство, парламент), а может быть и техническое устройство (например, автоматический регулятор, компьютер).

Последовательность команд по управлению объектом, приводящая к заранее поставленной цели, называется алгоритмом управления.

Простейшие алгоритмы управления могут состоять из одной команды или представлять собой линейную последовательность команд. Более сложные алгоритмы управления содержат ветвления и циклы.

3.6.2. Обратная связь

Для управления нужна информация. Во-первых, управляющий объект должен получить информацию о том, что ему нужно, т. е. он должен знать цель своих действий. Во-вторых, управляющий объект должен знать, как можно достичь поставленной цели

Важно, что информация о цели и способах её достижения должна быть известна управляющему объекту до начала процесса управления

Пример 1

Обратная связь — это процесс передачи информации о состоянии объекта управления в управляющую систему.

Обратная связь позволяет корректировать управляющие воздействия управляющей системы на объект управления в зависимости от состояния объекта управления. Обратная связь предусмотрена в ряде бытовых приборов (например, утюг с терморегулятором, холодильник, кастрюля-скороварка), в живых организмах, в обществе.

В настоящее время очень часто роль управляющей системы отводится компьютеру, в память которого заложена программа управления, предусматривающая все варианты информации, которые могут быть получены по обратной связи.

Пример 2. Если вместо обычного светофора на дорожном перекрёстке будет установлен «интеллектуальный» светофор — высокотехнологичное устройство, оснащённое датчиками, фиксирующими скорость движения на дороге и плотность транспортных потоков, то управление движением станет более рациональным за счёт учёта информации, поступающей от объекта управления (рис. 3.16).

Рис. 3.16. Кибернетическая модель управления

Самое главное

Управление — процесс целенаправленного воздействия на объект; осуществляется для организации функционирования объекта по заданной программе.

Последовательность команд по управлению объектом, приводящая к заранее поставленной цели, называется алгоритмом управления.

Вопросы и задания

1. Что такое управление? Приведите примеры управляющих систем и управляемых ими объектов.
2. Что такое алгоритм управления? Приведите примеры ситуаций, в которых имеют место линейные, разветвляющиеся и циклические алгоритмы.
3. Что изучает наука кибернетика?
4. Какая информация нужна для управления? Приведите пример.
5. Что такое обратная связь?
6. Опишите кибернетическую модель управления.

Способы записи алгоритмов

Алгоритмы можно представлять по-разному. Существую следующие способы записи алгоритмов:

• формульно-словесный – алгоритм задается с помощью естественного разговорного языка с использованием специальных знаков и формул;
• графический – алгоритм воспроизводится с применением графических объектов, выстроенных в виде блок-схемы;
• алгоритмический язык – алгоритм реализован посредством ключевых слов специального алгоритмического языка.

Рис. 2. Алгоритм, записанный на алгоритмическом языке.

Самым наглядным алгоритмом, является алгоритм, заданный в виде блок-схемы, где каждый шаг представлен определенной геометрической фигурой: прямоугольник заменяет вычислительный процесс, ромбом изображается условие, шестигранник используется для обозначения цикла с известным числом повторов.

Рис. 3. Блок-схема алгоритма.

при разработке блок-схем алгоритмов следует пользоваться правилами, регламентированными в специальном стандарте. На территории РФ функционирует Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем».

Что мы узнали?

Алгоритм представляет собой цепочку команд, приводящих к определенному результату. Он обладает свойствами массовости, дискретности, конечности, однозначности. Алгоритмы могут быть заданы в виде блок-схем, а также описаны с помощью естественных и специальных алгоритмических языков.

1. /5

   Вопрос 1 из 5

   Что называется алгоритмом:

   • Набор инструкций, выполнение которых приведет к достижению результата.
   • Совокупность однотипных объектов
   • Список номенклатурных наименований
   • Перечень объектов

Алфавит QBASIC

Алфавит
Qbasic включает следующие наборы
символов:

• латинские буквы;

• русские буквы (только для записи
  комментариев к программе и текстовых констант);

• цифры;

• специальные символы.

 Специальные символы: 

Символ	Назначение
Арифметические действия
(    )	Скобки; действия в скобках выполняются в первую очередь.
^	Возведение в степень; 53 записывается как 5^3.
*	Умножение
Деление
\  или MOD	Целочисленное деление ( 9 \ 2=4).
DIV	Остаток от деления  (9 DIV 2 = 1)
+	Сложение
—	Вычитание
Операции сравнения
=	Равно
>	Больше
<	Меньше
>=	Больше или равно
<=	Меньше или равно
<>	Не равно
Логические операции
NOT	Логическая операция НЕ
AND	Логическая операция  И
OR	Логическая операция ИЛИ
Другие символы
“”	Текстовая константа
‘	Начало комментария к программе
$	Текстовый тип данных
%	Целый тип данных
,  :  ;	Разделители (в разных случаях используют разные знаки для разделения однотипных элементов строки).
.	Отделяет целую часть числа от десятичной дроби.

Операторы

 Операторы описания и объявления

DIMсписок — служит для описания
переменных и массивов. Обязательно только описание массивов.

DECLARE SUB
имя (формальные
параметры)— объявляет процедуру.

 Операторы ввода данных.

INPUT “приглашение”;
список переменных — служит для ввода данных с
клавиатуры, например:

        INPUT”Введите массу и
ускорение”; m,a

 Когда в
программе встречается такой оператор, компьютер
приостанавливает  выполнение программы, выдает на экран текст
приглашения и ждет ввода данных. Данные вводятся с клавиатуры
пользователем программы. Их количество и тип должны
соответствовать списку переменных! Совместно с оператором 
INPUT удобно использовать операторы
COLOR  LOCATE.
Первый регулирует цвет текста, а второй местоположение текста на
экране. Например, чтобы вводить данные из центра экрана, а
приглашение печаталось красным цветом, можно применить следующий
фрагмент программы:

COLOR 4

LOCATE  14, 35

INPUT “Введите массу и ускорение “;
m,a

DATA
список данных

READ
список переменных

Служат для автоматического ввода данных из программы. Оператор 
DATA  должен предшествовать оператору
(или операторам)  READ. Чтение данных
производится последовательно.

Оператор
присваивания

 Имя переменной
=
выражение

Присваивает переменной, имя которой находится
слева от знака = (знак присваивания) значение выражения 
находящегося справа. Старое значение переменной при этом
теряется. Например:

A = A + 1

Берется значение переменной А, к нему добавляется единица,
полученное значение записывается обратно в переменную А

Операторы вывода
данных.

PRINT
список вывода — служит для вывода
текстовых и числовых  данных на экран. Список для вывода
может включать в себя константы, переменные и выражения.
Константы выводятся без изменений, вместо переменных и выражений
печатаются их текущие значения. Совместно с
PRINT  удобно использовать операторы
LOCATE  COLOR. Например:

COLOR 2

LOCATE 15, 35

PRINT  “Сила =”;
F; “H”

В результате выполнения программы в центре экрана зелёным цветом
будет выведено:

Сила = 129.81 H

BEEP— выводит звуковой сигнал.

SOUND
частота, длительность — выводит звуковой сигнал
заданной длительности и частоты.

PLAY”символьное
выражение” — позволяет
создавать музыкальные фрагменты (см. справку  Qbasic).

SCREEN
номер— включает графический режим. Допустимые номера
режимов 1,2,8,9,12. Наилучшее качество изображения (640*480
пикселей, 16 цветов) обеспечивает  12 режим.

CLS— очищает экран.

LINE
(x1,
y1)-(x2,
y2),
цвет — рисует линию от точки Х1,У1 до Х2,У2 указанным
цветом.

LINE (x1,
y1)-(x2,
y2),
цвет, b— рисует рамку с углами в точках Х1,У1 и Х2,У2 указанным
цветом.

LINE (x1,
y1)-(x2,
y2),
цвет, bf— рисует закрашенный прямоугольник.

PSET (x,
y),
цвет — устанавливает точку.

CIRCLE (x,
y),
радиус, цвет
— рисует окружность с центром в точке Х,У указанного цвета и
радиуса.

PAINT (x,y),
c1,
c2 — выполняет заливку
начиная с точки Х,У цветом С1. Заливка ограничивается линией
цвета С2.

DRAW”символьное
выражение” – позволяет
создавать сложные рисунки (см. справку 
Qbasic).

 Операторы
переходов

GOTO 
Метка — передает управление на строку с указанной
меткой.

GOSUB
Метка — передает управление в подпрограмму,
начинающуюся с указанной метки.

 RETURN
— возвращает управление после окончания подпрограммы, в основную
программу.

EXIT
— передает управление на строку, следующую за концом
текущей структуры.

CALL 
Имя (фактические
параметры) — передает
управление процедуре с указанным именем и фактическими
параметрами.

 Оператор
конца программы

Свойства алгоритма

Понятность — инструкции, используемые в алгоритме, должны быть понятны исполнителю, т.е.
алгоритм должен включать только действия (команды), известные исполнителю.

Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

Определенность (детерминированность) — предполагает получение однозначного результата вычислительного процecca при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер.
Для этого на каждом шаге алгоритма не должно возникать разночтений и разногласий, т.е. инструкции должны быть четко определены.

Завершаемость (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов, т.е.
алгоритмы конечны, они должны завершаться и выдавать результат за заранее известное число шагов.

Результативность — завершение алгоритма определенным результатом, т.е.
выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет!

Массовость — алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.

Слайд 3 В

настоящее время под компьютерной моделью чаще всего понимают:• условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т. д. и отображающий структуру и взаимосвязи между элементами объекта. Компьютерные модели такого вида мы будем называть структурно-функциональными;• отдельную программу, совокупность программ, программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных (как правило, случайных) факторов. Такие модели мы будем далее называть имитационными моделями. Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели.Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели.

Слайд 16Виды алгоритмов Виды алгоритмов как логико-математических средств в зависимости от цели,

начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом: механические алгоритмы, иначе детерминированные; гибкие алгоритмы, иначе вероятностные и эвристические.     Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса или задачи, для которых разработан алгоритм.    Эвристический алгоритм — это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий исполнителя. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и опыте решения схожих задач.

Операторы — структуры

IF  условие
THEN
Оператор— если условие – истина, то
выполняется оператор после ключевого слова 
THEN. Затем управление передаётся на следующую строку
программы. Если условие – ложь, то управление сразу передается
на следующую строку программы.

IF
условие THEN

      Группа операторов

END IF

 — если условие – истина, то выполняется группа операторов
между  THEN и END
IF. Затем управление передаётся на следующую за
END IF  строку  программы. Если
условие – ложь, то управление сразу передается на следующую за
END IF строку программы.

IF
условие THEN
оператор_1
ELSE оператор_2 
— если условие – истина, то выполняется оператор1, иначе
выполняется оператор2  . Затем управление передаётся на
следующую строку программы.

IF
условие THEN

        Группа операторов 1

ELSE

        Группа операторов 2

END IF

 — если условие – истина, то выполняется блок операторов 1,
иначе выполняется блок операторов 2  . Затем управление
передаётся на следующую за  END IF 
строку программы. 

SELECT CASE
выражение для сравнения

   CASE
условие 1

      Группа операторов 1

   CASE
условие 2

      Группа операторов 2

………….

   ELSE CASE

      Группа операторов  N

END SELECT

— если  условие 1 — истина, то выполняется блок операторов 1 и
осуществляется переход на строку программы, следующую за 
END SELECT; если условие 2 — истина,
то выполняется блок операторов 2  и осуществляется переход на
строку программы, следующую за   END SELECT
и т. д., если все условия – ложь, то выполняется блок
операторов   N  и осуществляется
переход на строку программы, следующую за 
END SELECT.

 DO 
WHILE   условие   DO                                 
       WHILE 
условие

Группа операторов                     Группа операторов              Группа операторов

LOOP                                         
LOOP
WHILE  условиеWEND

— выполняет группу операторов, пока условие – истина
(такие циклы называются циклами «ПОКА»).

DO UNTIL 
условие                 DO

Группа операторов                      Группа операторов

LOOP                                             LOOP
UNTIL условие

— выполняет группу операторов до выполнения
условия (такие циклы называются циклами «ДО»).

FOR
Параметр = Начальное
значение TO
 Конечное значение
STEP шаг

Группа операторов

NEXT
Параметр

— выполняет группу операторов фиксированное число раз.
Количество повторений зависит от начального значения и конечного
значения параметра, а также шага.  Переменная – параметр
изменяется от начального значения,  увеличиваясь (или
уменьшаясь, если шаг отрицательный) каждый раз на
величину шага. Цикл завершает работу, когда значение параметра
достигает (или превышает) конечное значение.

SUB
Имя (формальные параметры)

  Группа операторов

END SUB

—  содержит группу операторов – процедуру; обращение к
процедуре выполняется оператором САLL.
К одной и той же процедуре можно обращаться многократно, задавая
при этом различные фактические параметры.

Графическое изображение алгоритмов

Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.

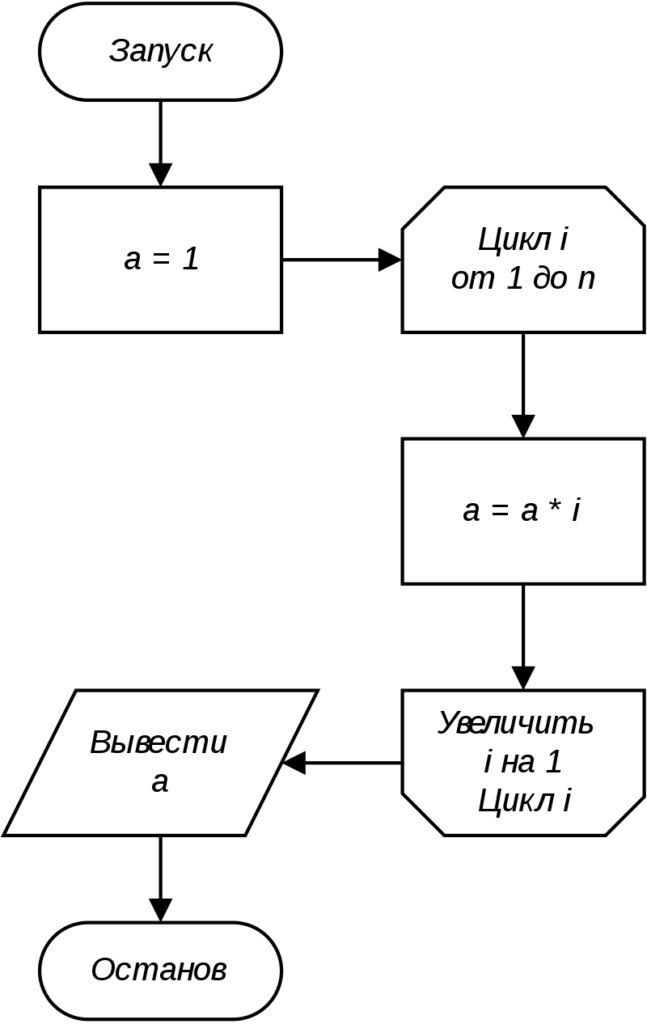
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.

Слайд 8 1. уч.

вопрос. Формализация моделей Процесс построения информационных моделей с помощью формальных языков называется формализацией. В процессе исследования формальных моделей часто производится их визуализация. (?) Для визуализации алгоритмов используются блок-схемы, пространственных соотношений между объектами — чертежи, моделей электрических цепей — электрические схемы. При визуализации формальных моделей с помощью анимации может отображаться динамика процесса, производиться построение графиков изменения величин и т. д. В настоящее время широкое распространение получили компьютерные интерактивные визуальные модели. В таких моделях исследователь может менять начальные условия и параметры протекания процессов и наблюдать изменения в поведении модели.