Геометрия

Прямоугольник: определение и примеры

Основные характеристики прямоугольника:

• Два параллельных противоположных стороны. Прямоугольник имеет две пары противоположных сторон, которые параллельны друг другу.
• Равные противоположные стороны. Каждая пара противоположных сторон прямоугольника равна по длине, что делает его симметричным относительно центра.
• Диагонали равны и перпендикулярны. Диагонали прямоугольника пересекаются в его центре, делят его на два равных треугольника и являются перпендикулярными друг другу.

Примеры прямоугольников:

• Прямоугольник ABCD. В этом примере, точки A, B, C и D образуют прямоугольник, где AB и CD, а также AD и BC являются параллельными сторонами.
• Квадрат. Квадрат является особым случаем прямоугольника, где все стороны равны по длине.
• Прямоугольная плитка. Прямоугольная плитка, которую мы часто видим на полу или на стенах, также является примером прямоугольника.

Формула угла правильного многоугольника

Существует закономерность, согласно которой можно рассчитать угол правильного многоугольника. Известно, что для любого выпуклого n-угольника сумма углов составляет \(180^{0}(n-2)\). Предположим, что угол правильного многоугольника обозначен \alpha. Исходя из того, что у такой геометрической фигуры n углов, и они равны, можно записать следующее равенство:

\(n*\alpha =180^{0}(n-2)\)

Из записанного выражения можно выразить \(\alpha\), то есть записать формулу угла правильного многоугольника:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

В данном случае n обозначает число сторон многоугольника.

Справедливость записанной формулы можно проверить на примере равностороннего треугольника и квадрата. В случае треугольника n=3, а угол составляет \(60^{0}\). Его можно определить по формуле:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(3-2)}{3}=\frac{180^{0}*1}{3}=60^{0}\)

В случае квадрата, у которого n=4, угол равен \(90^{0}\), что легко рассчитать:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(4-2)}{4}=\frac{180^{0}*2}{4}=90^{0}\)

Используя данную закономерность можно определить углы других правильных многоугольников.

Угол правильного пятиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(5-2)}{5}=\frac{180^{0}*3}{5}=108^{0}\)

Угол правильного шестиугольника составляет:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(6-2)}{6}=\frac{180^{0}*4}{6}=120^{0}\)

Угол правильного восьмиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(8-2)}{8}=\frac{180^{0}*6}{8}=135^{0}\)

В случае правильного многоугольника с 50 углами, каждый угол составит:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(50-2)}{50}=\frac{180^{0}*48}{50}=172,8^{0}\)

Далее в качестве примера использования формулы угла правильного n-угольника можно рассмотреть задачу на определение числа сторон у правильного многоугольника, каждый угол которого составляет \(179^{0}.\)

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(179=\frac{180(n-2)}{n}\)

\(179n=180(n-2)\)

\(179n=180n-360\)

\(179n-180n=-360\)

\(-n=-360\)

\(n=360\)

Таким образом, рассматриваемый правильный многоугольник обладает 360 сторонами.

С помощью формулы угла правильного многоугольника можно определить, существует ли такой правильный многоугольник, угол которого составляет \(145^{0}\). В том случае, когда такая геометрическая фигура существует, формула примет вид:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(145=\frac{180(n-2)}{n}\)

\(145n=180(n-2)\)

\(145n=180n-360\)

\(145n-180n=-360\)

\(-35n=-360\)

\(n=\frac{360}{35}=\frac{72}{7}=10\frac{2}{7}\)

Правильные четырехугольники и их особенности

Четырехугольник называется правильным, если все его стороны и углы равны. Правильные четырехугольники имеют некоторые особенности, которые делают их уникальными и интересными.

Одним из наиболее известных и изученных правильных четырехугольников является квадрат. У квадрата все четыре стороны равны, и все его углы прямые. Квадрат также обладает свойством диагоналей, которые равны и перпендикулярны друг другу.

Еще одним примером правильного четырехугольника является ромб. У ромба все четыре стороны равны, но его углы не обязательно прямые. Ромб также обладает свойством диагоналей, которые перпендикулярны друг другу и делят углы ромба пополам.

Трапеция — это еще один пример правильного четырехугольника. Трапеция имеет две параллельные стороны и две непараллельные стороны. Трапеция также имеет одну пару углов, которые сумма их равна 180 градусов.

Наконец, параллелограмм также является правильным четырехугольником. У параллелограмма все стороны равны, и его противоположные стороны параллельны. Параллелограмм также обладает свойством диагоналей, которые делятся пополам и пересекаются под прямым углом.

В заключение, правильные четырехугольники представляют собой уникальную категорию геометрических фигур. Изучение их особенностей и свойств помогает лучше понять строение и взаимосвязи между сторонами и углами этих фигур.

Название	Строение	Особенности
Квадрат	Все стороны и углы равны	Диагонали равны и перпендикулярны друг другу
Ромб	Все стороны равны, углы не обязательно прямые	Диагонали перпендикулярны друг другу и делят углы ромба пополам
Трапеция	Две параллельные стороны, две непараллельные стороны	Сумма углов равна 180 градусов
Параллелограмм	Все стороны равны, противоположные стороны параллельны	Диагонали делятся пополам и пересекаются под прямым углом

Названия четырехугольников в разных странах

В разных странах четырехугольники могут называться по-разному. Ниже приведены некоторые названия четырехугольников из разных культур и математических традиций:

1. Прямоугольник — в России и большинстве стран этот четырехугольник с двумя парами параллельных сторон и четырьмя прямыми углами называется «прямоугольником».

2. Квадрат — частный случай прямоугольника, у которого все стороны и углы равны. Название «квадрат» используется во многих странах.

   

   

   

   

   

   

   

   

   

   

3. Ромб — четырехугольник, у которого все стороны равны. В странах говорящих на английском языке и в некоторых других странах, такой четырехугольник называется «ромб».

4. Трапеция — четырехугольник, у которого есть хотя бы две параллельные стороны. В некоторых странах такой четырехугольник называется «трапецией».

5. Параллелограмм — четырехугольник, у которого противоположные стороны параллельны. Название «параллелограмм» используется во многих странах.

Это лишь некоторые примеры названий четырехугольников, которые могут использоваться в разных странах. Интересно, какие названия еще можно встретить в других культурах и языках.

Четырехугольник: определение и свойства

У четырехугольника есть несколько важных свойств:

1. Сумма внутренних углов четырехугольника равна 360 градусам.
2. Стороны четырехугольника могут быть равными или неравными друг другу.
3. Углы четырехугольника могут быть прямыми, тупыми или острыми.
4. Четырехугольник может быть выпуклым или невыпуклым. Если все его углы выпуклые, то четырехугольник называется выпуклым. Если хотя бы один угол невыпуклый, то четырехугольник называется невыпуклым.

Прямоугольник

Синонимы слова «прямоугольник»:

Квадрат	Прямоугольная фигура
Прямоугольное поле	Прямоугольная площадка
Прямоугольное озеро	Прямоугольная форма

Квадрат

Вот основные характеристики квадрата:

• Все стороны квадрата имеют одинаковую длину. Это делает его стороны параллельными и равными.
• Все углы квадрата равны между собой и равны 90 градусам.
• Диагонали квадрата являются радиусами окружности, описанной вокруг него. Они имеют равную длину и делят углы квадрата на две равные части.

Ромб

В ромбе все углы равны между собой и каждый из них составляет по 90 градусов. Ромб также имеет две диагонали, которые пересекаются в точке, называемой центром ромба. Диагонали равны по длине и делят ромб на четыре равные треугольные зоны.

Синонимы	Пояснение
Ромбус	О другом названии ромба
Квадрат	Иногда неправильно называется ромб

Ромб широко используется в архитектуре и дизайне, благодаря своим симметричным и гармоничным формам. Он также является основой для множества геометрических задач и теорем.

Основные свойства, определение правильного n-угольника

Правильный n-угольник представляет собой особый вид многоугольника с равными между собой сторонами и углами.

Существует формула, с помощью которой можно определить его длину при известном радиусе вписанной в него окружности:

\(\alpha =2r*\tan \frac{180^{0}}{n}\)

\(\alpha =2r*\tan \frac{\pi }{n}\)

При этом радиус вписанной окружности n-угольника определяют через длину стороны:

\(r=\frac{a }{2\tan \frac{180^{0}}{n}}\)

\(r=\frac{a }{2\tan \frac{\pi }{n}}\)

Сторону правильного n-угольника можно определить на основании радиуса описанной вокруг него окружности:

\(a=2R*\sin \frac{180^{0}}{n}\)

\(a=2R*\sin \frac{\pi }{n}\)

Таким образом, радиус описанной окружности n-угольника составляет:

\(R=\frac{a}{2\sin \frac{180^{0}}{n}}\)

\(R=\frac{a}{2\sin \frac{\pi }{n}}\)

Площадь правильного n-угольника можно определить, зная длину стороны, по формуле:

\(S=\frac{na^{2}}{4}*ctg\frac{180^{0}}{n}\)

При известном радиусе вписанной окружности, площадь n-угольника равна:

\(S=nr^{2}*\tan \frac{180^{0}}{n}\)

Если известен радиус описанной окружности, то площадь n-угольника определяется по формуле:

\(S=\frac{nR^{2}}{2}*\sin \frac{360^{0}}{n}\)

Периметр правильного n-угольника составляет:

\(P=na\)

Определить угол между сторонами правильного n-угольника можно с помощью формулы:

\(\alpha _{n}=\frac{n-2}{n}*180^{0}\)

Известно, что треугольник можно задать с помощью длин трех его сторон. Однако в случае правильного треугольника необходимо знать только одну длину стороны, так как все правильные треугольники подобны. Таким образом, при отсутствии данных о масштабе или метрики, правильные треугольники эквивалентны друг другу.

Такими же свойствами обладает квадрат, то есть правильный четырехугольник.

В качестве примеров таких геометрических фигур можно рассмотреть правильные пяти, шести и сколь угодно большие n-угольники. Предельным случаем при бесконечно увеличивающемся n является окружность. Для всех таких многоугольников характерны следующие свойства:

• геометрические фигуры задают с помощью одного параметра, то есть длиной элемента;
• рассматриваемые многоугольники подобны всем многоугольникам своего класса.

В геометрии можно встретить разные виды правильных n-угольников. Все они обладают не только одним параметром, с помощью которого задаются, но и характеризуются осями и центром симметрии. Правильный треугольник возможно три раза повернуть вокруг центра. При этом разница между данными положениями отсутствует.

Квадрат можно повернуть таким же способом четыре раза. Предельным случаем является окружность, которую можно повернуть бесконечное число раз, но результат при этом не изменится, то есть данная геометрическая фигура обладает бесконечным количеством осей симметрии.

В природе невозможно найти идеальную окружность или любой другой правильный n-угольник. В реальности предметы рассматривают лишь в качестве их приближений. Однако многие практические задачи характеризуются достаточно точным приближением, что позволяет применять правильные многоугольники в их решении, как полезный инструмент. Свойства таких геометрических фигур изучают и фиксируют.

В дальнейшем при рассмотрении окружности в качестве предельного случая правильных n-угольников эти свойства переносят на нее для получения полезных утверждений не для ломаной, а для гладкой кривой.

Известно, что равносторонний треугольник представляет собой правильный треугольник. Необходимо выяснить, является ли любой равносторонний многоугольник также правильным многоугольником.

Напомним, что правильными многоугольниками являются те, которые имеют равные стороны и равные углы.

В случае треугольника достаточным условием является равенство сторон. Так как из этого следует равенство его углов. При рассмотрении других n-угольников это утверждение не верно.

Отличия между синонимами

Существует несколько синонимов для определения правильного четырехугольника, но каждый из них имеет некоторые отличия:

• Квадрат: это четырехугольник, у которого все стороны равны и все углы прямые.
• Ромб: это четырехугольник, у которого все стороны равны, но все углы не обязательно прямые.
• Прямоугольник: это четырехугольник, у которого все углы прямые, но не все стороны равны.
• Параллелограмм: это четырехугольник, у которого противоположные стороны параллельны, но не обязательно равны.

Хотя все эти термины связаны с правильным четырехугольником, каждый из них обращает внимание на разные его характеристики. Поэтому, при описании четырехугольников, кроме основного термина «правильный четырехугольник», стоит учитывать и эти различные синонимы

Прямоугольник

Синонимы для прямоугольника:

• Прямоугольная фигура
• Четырехугольник с прямыми углами
• Фигура с параллельными сторонами и прямыми углами
• Фигура с четырьмя прямыми углами

Квадрат

В геометрии квадрат обозначается буквой ‘S’ и обычно имеет форму таблицы, где все стороны и углы равны друг другу. Площадь квадрата равна квадрату длины его стороны, а периметр равен четырем удвоенным сторонам квадрата.

Синонимы слова «квадрат» — перекладина, карьер, доска, подпора, отпор, подмост, мостовая, перекресток, жбан, мостик, переборка. В разных сферах эти слова могут использоваться как синонимы для квадратного образа или формы. Например, в строительстве используется термин «плита квадратная» для обозначения квадратного элемента предмета или конструкции.

Ромб: особенности и применение

Ромб обладает несколькими особенностями, которые делают его уникальным и полезным в различных областях:

Стороны	Все стороны ромба равны между собой, что делает его симметричным и эстетически привлекательным.
Углы	Все углы ромба равны 90 градусов, что делает его периметр простым в вычислении.
Диагонали	Диагонали ромба перпендикулярны друг другу и делят его на четыре равных треугольника. Это свойство делает ромб удобным для проведения геометрических конструкций.
Площадь	Площадь ромба можно вычислить, зная длину одной из его сторон и высоту, опущенную на нее.

Ромб находит применение в различных областях:

• Архитектура: ромб используется в дизайне зданий, фасадах и оконных рамах.
• Геометрия: ромб является одним из базовых геометрических фигур и используется для изучения и доказательства различных математических теорем.
• Украшения: ромбы часто применяются в ювелирных украшениях, таких как колечки, серьги и ожерелья.
• Логотипы и брендинг: ромб может использоваться в логотипах компаний для передачи определенных символических идей и ценностей.
• Знаки дорожного движения: ромб используется для обозначения определенных дорожных знаков, например, знака «Встречное движение запрещено».

Таким образом, ромб не только привлекателен с эстетической точки зрения, но и имеет множество практических применений в различных областях.

Признаки и свойства правильного многоугольника

Многоугольник можно считать правильным в том случае, когда все его стороны и углы одинаковы. Таким образом, должно выполняться правило:

\(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)

\(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)

Существуют основные свойства, характерные для правильных многоугольников.

1. Все стороны правильного многоугольника равны, то есть: \(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)
2. Углы правильного многоугольника равны, то есть: \(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)
3. Центр вписанной в правильный многоугольник окружности \(O _{B}\) соответствует центру описанной вокруг этого многоугольника окружности \(O _{O}\), что в результате образует центр многоугольника О
4. Сумма всех углов n-угольника составляет: \(180^{0}*(n-2)\)
5. Внешние углы n-угольника в сумме равны 360^{0} или \(\beta _{1} + \beta _{2} + \beta _{3} + … + \beta _{n-1} + \beta _{n} = 360^{0}\)
6. Число диагоналей \(D _{n}\), которыми обладает n-угольник, соответствует половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины, то есть: \(\beta _{1}=\frac{n*(n-3)}{2}\)
7. В правильный многоугольник можно вписать окружность и описать круг. При этом площадь кольца, сформированного данными окружностями, определяется лишь длиной стороны многоугольника, то есть: \(S=\frac{\pi }{4}a^{2}\)
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника О.

правильный четырехугольник

Смотреть что такое «правильный четырехугольник» в других словарях:

ПОНЯТИЕ — общее имя с относительно ясным содержанием и сравнительно четко очерченным объемом. П. являются, напр., «химический элемент», «закон», «сила тяготения», «астрономия», «поэзия» и т.п. Отчетливой границы между теми именами, которые можно назвать П … Философская энциклопедия

Боппард — (Boppard) городок на левом берегу Рейна, в прусском округе Кобленце, в 13 км от города Ст. Гоар, имеет 5526 жителей, занимающихся горшечным промыслом, винокурением, а также виноградарством и торговлей дровами и углем. Во времена римлян на этом… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Конотоп — у. гор. Черниговской губ., в юго вост. углу губернии, на pp. Конотопе и Езусе. Городской земли в гор. черте 751/2 дес. Жит. 23083 (11632 мжч. и 11451 жнщ.). 2037 деревян. и 55 камен. зданий (кроме церквей). Средний доход за 1870 74 гг. 6202 руб … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Спалато — (хорватск. Spljet или Split, итал. Spalato, в памятниках также Spalatro) самый важный порт Далмации, расположен на полуострове Адриатического моря, омывается с северной стороны Canale Castelli, с южной Canale di Spalato, y подножия горы Monte… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Убор головной* — термин, включающий как способы собственно прически, так и способы убранства и покрытия головы. И те, и другие в высшей степени разнообразны в зависимости от расы, места, эпохи, религии, степени культуры и умственного развития. Тем не менее как… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Убор головной — термин, включающий как способы собственно прически, так и способы убранства и покрытия головы. И те, и другие в высшей степени разнообразны в зависимости от расы, места, эпохи, религии, степени культуры и умственного развития. Тем не менее как… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Введенская улица — Введенская улица находится на Петроградской стороне. Она соединяет Кронверкский и Большой проспекты. Первоначально, в 1730 е годы, она именовалась 2 й Большой Белозерской, поскольку находилась в слободе Белозерского полка. Второй… … Санкт-Петербург (энциклопедия)

Стрельна — исторический памятник, поселок на южном берегу Финского залива, расположен в 19 км к западу от Петербурга (см. Санкт Петербург). Административно Стрельна подчинена Петродворцу (см. Петродворец). Мыза Стрельна вблизи речки Стрелки, впадающей в… … Географическая энциклопедия

Медининкайский замок — Медининкайский замок … Википедия

Построение правильных многоугольников

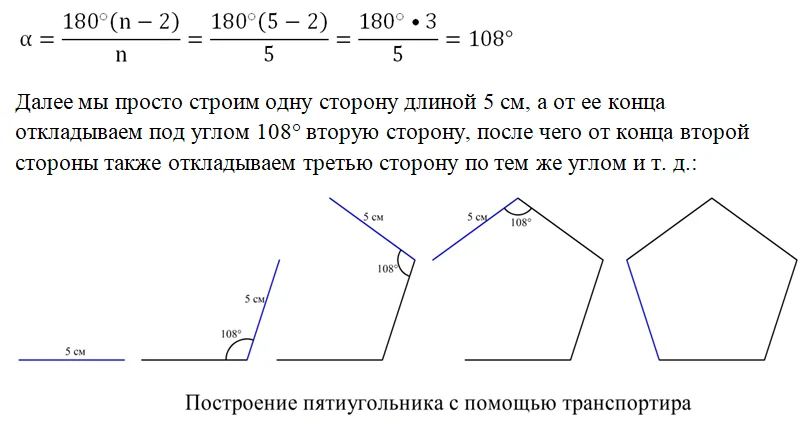
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

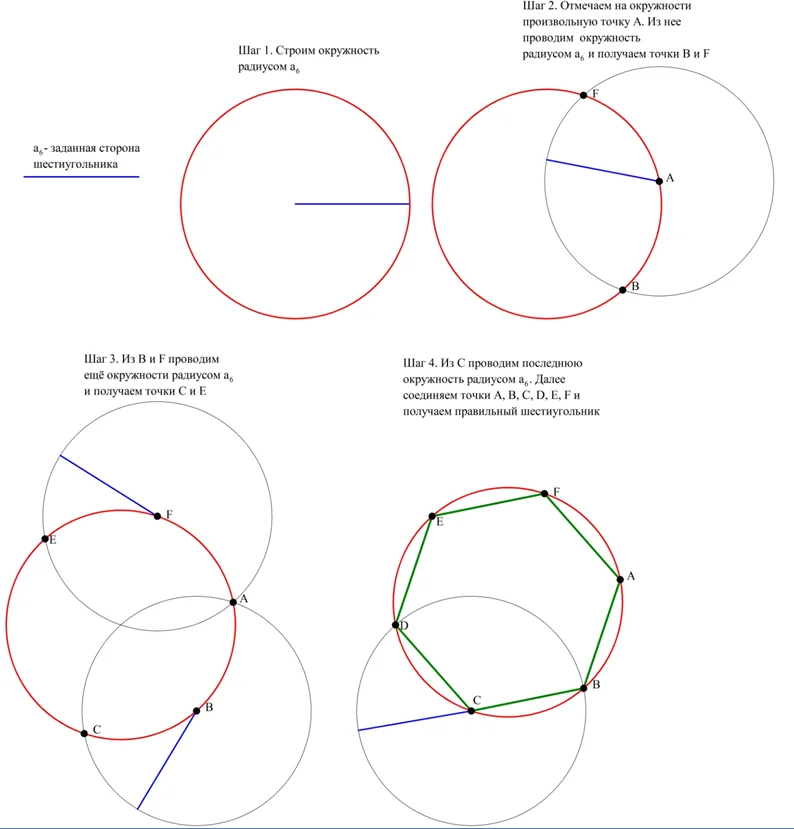
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах

Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности

Параллелограмм: четырехугольник с параллельными сторонами

Параллелограмм — это особый тип четырехугольника, у которого все стороны параллельны попарно. Он имеет несколько характеристик, которые делают его отличным от других четырехугольников.

Основные характеристики параллелограмма:

• Все стороны параллельны попарно.
• Противоположные стороны равны.
• Противоположные углы равны.
• Сумма углов параллелограмма равна 360 градусов.

Из-за параллельности сторон параллелограмм обладает несколькими интересными свойствами. Углы между параллельными сторонами равны и противоположные стороны параллельны и равны.

Параллелограмм можно классифицировать на основе дополнительных характеристик:

1. Прямоугольник: параллелограмм с прямыми углами.
2. Квадрат: параллелограмм, у которого все стороны равны и все углы прямые.
3. Ромб: параллелограмм, у которого все стороны равны.

Параллелограммы много встречаются в повседневной жизни. Книжные полки, дверные коробки, оконные рамы — все они могут быть параллелограммами.

В заключение, параллелограмм — это четырехугольник с параллельными сторонами. Он обладает рядом уникальных свойств и может быть прямоугольником, квадратом или ромбом, в зависимости от наличия дополнительных характеристик.

Понятие правильного четырехугольника и его особенности

Правильный четырехугольник — это четырехугольник, у которого все стороны равны между собой и все углы равны 90 градусов. Такой четырехугольник еще называется квадратом.

Особенности правильного четырехугольника:

1. У него все стороны равны.
2. У всех углов правильного четырехугольника равна величина — 90 градусов.
3. Диагонали правильного четырехугольника равны между собой и делят его на четыре равных прямоугольных треугольника.
4. У правильного четырехугольника все диагонали являются его симметричными осями.
5. Правильный четырехугольник можно вписать в окружность, при этом все его вершины лежат на окружности.

Примеры правильных четырехугольников:

• Квадрат со стороной 5 см.
• Квадрат со стороной 10 м.
• Квадрат со стороной 2.5 дм.

Прямоугольник: две пары равных сторон и прямые углы

Прямоугольник является особой формой четырехугольника, где все стороны пересекаются под прямыми углами. Эти свойства делают прямоугольник одной из самых распространенных и полезных геометрических фигур.

В геометрии прямоугольник часто используется для вычисления площади и периметра фигуры. Для этого достаточно знать длины двух сторон прямоугольника.

Прямоугольник также является основой для построения многих других геометрических фигур. Например, квадрат является особым видом прямоугольника, где все стороны равны.

Использование прямоугольника в различных областях, таких как архитектура, строительство, графика, позволяет создавать прочные и устойчивые конструкции.

Определение и особенности правильного четырехугольника

Вот основные особенности и определения правильного четырехугольника:

• Все стороны правильного четырехугольника равны между собой. Это значит, что длина каждой стороны одинакова.
• Все углы правильного четырехугольника равны между собой. Поэтому угол, образованный каждыми двумя соседними сторонами, имеет одинаковую величину.
• Каждая диагональ правильного четырехугольника является симедианой — линией, которая делит диагональ пополам и перпендикулярна ей.
• Сумма внутренних углов правильного четырехугольника равна 360 градусов.

Правильные четырехугольники являются геометрическими фигурами с симметрией и регулярной формой. Они встречаются в различных областях науки и искусства, используются в архитектуре, дизайне и геометрии.

Четырехугольник: как называется?

Четырехугольник — это фигура, которая имеет четыре стороны, четыре угла и четыре вершины. В зависимости от своих особенностей и свойств, четырехугольники могут иметь различные названия. Рассмотрим пять наиболее распространенных названий для четырехугольников:

1. Прямоугольник:

   Прямоугольник — это четырехугольник, у которого все четыре угла прямые (равны 90 градусов). Прямоугольник также имеет противоположные стороны, которые параллельны и равны друг другу.

2. Квадрат:

   Квадрат — это прямоугольник, у которого все четыре стороны равны между собой. Квадрат также имеет все углы прямые (равны 90 градусов).

3. Параллелограмм:

   Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны между собой. Параллелограммы могут иметь углы различных величин.

4. Ромб:

   Ромб — это параллелограмм, у которого все стороны равны между собой. Ромб также имеет все углы равными.

5. Трапеция:

   Трапеция — это четырехугольник, у которого хотя бы две стороны параллельны друг другу. Трапеции могут иметь углы различных величин.

Это лишь некоторые из возможных названий для четырехугольников. В дополнение к вышеперечисленным названиям, существуют и другие типы четырехугольников, такие как ромбоид, трапецоид и пятиугольник.

Примеры правильных четырехугольников

Правильный четырехугольник, также известный как квадрат, — это четырехугольник, у которого все стороны равны и все углы прямые. Вот несколько примеров правильных четырехугольников:

• Квадрат: самый известный пример правильного четырехугольника. У него четыре равных стороны и четыре прямых угла.

• Ромб: это четырехугольник, у которого все стороны равны. Он также имеет две пары параллельных сторон и четыре угла.

• Прямоугольник: это четырехугольник, у которого все углы прямые. Он может иметь две пары параллельных сторон.

• Трапеция: это четырехугольник, у которого хотя бы две стороны параллельны. Он может быть и правильным, и не правильным.

Это только некоторые примеры правильных четырехугольников. Существует еще большое множество других типов четырехугольников, каждый со своими уникальными свойствами.