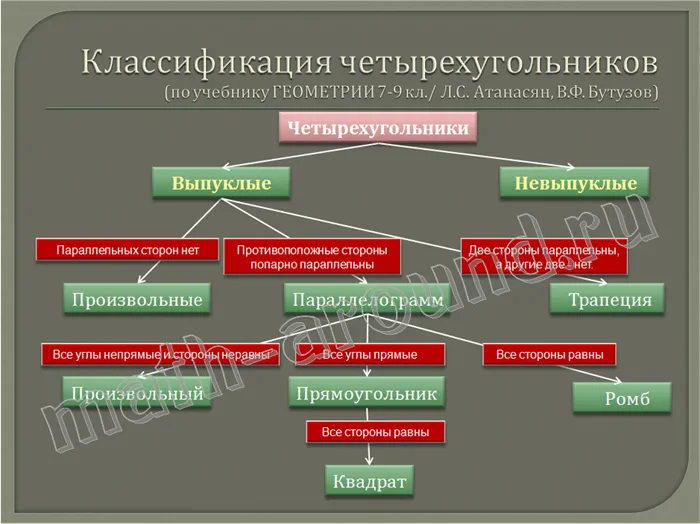
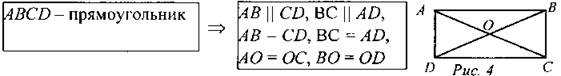Все о параллелограмме
| Чем отличаются свойства от признаков?Свойства нельзя путать с признаками, хоть они и очень похожи. Например, свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, а признаки предназначены для выявления параллелограммов среди четырехугольников. |
Свойства параллелограмма
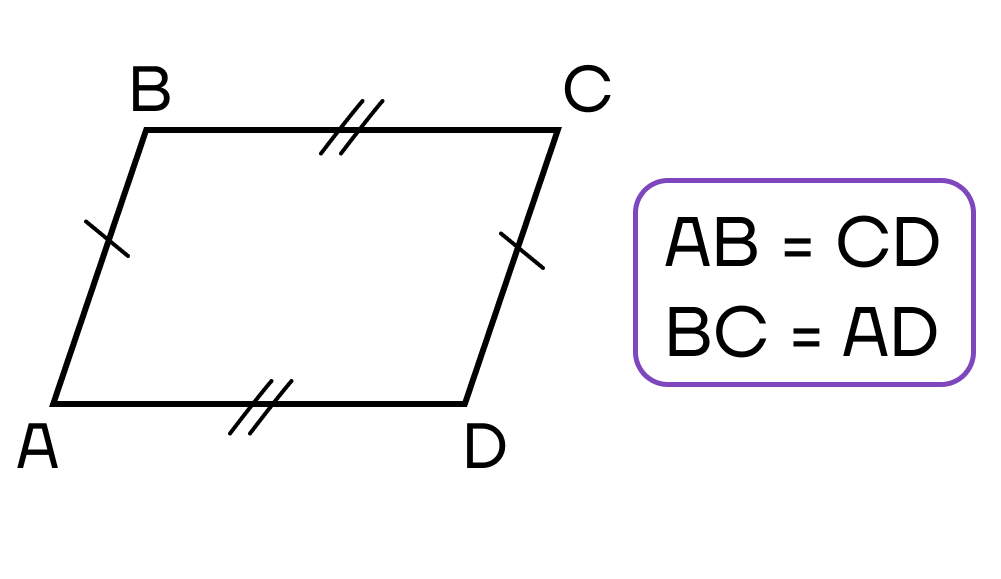
- Противолежащие стороны равны.
- Противолежащие стороны параллельны.
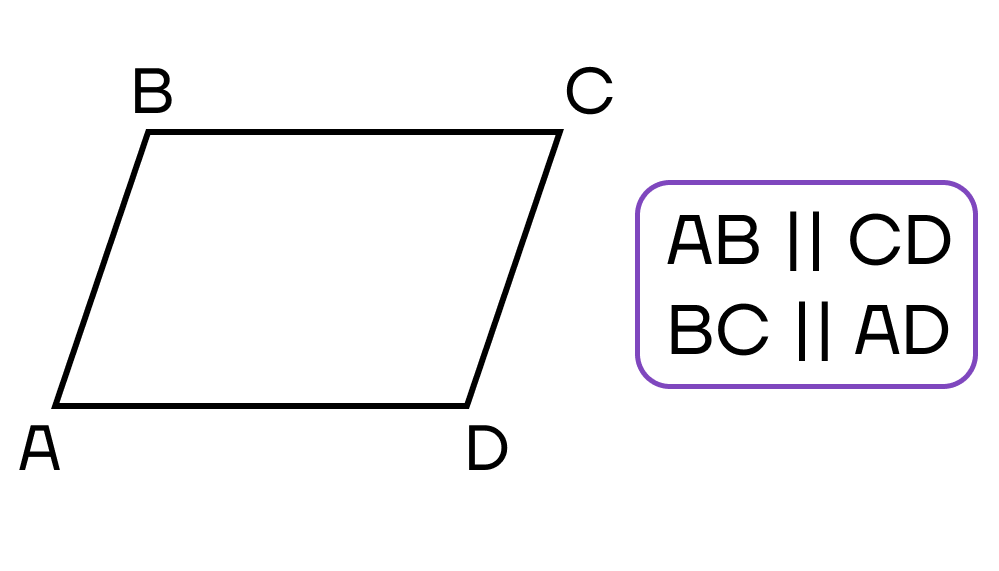
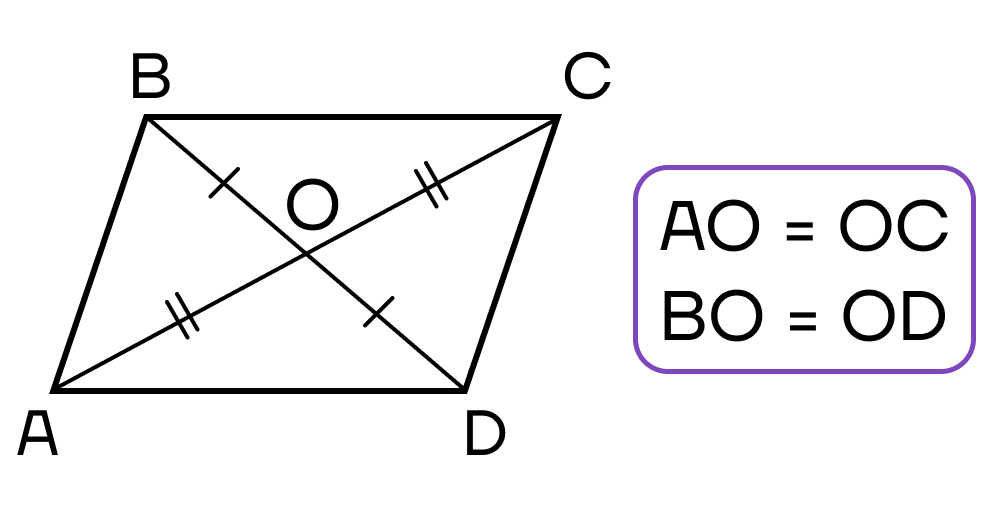
- Диагонали пересекаются и точкой пересечения делятся пополам.
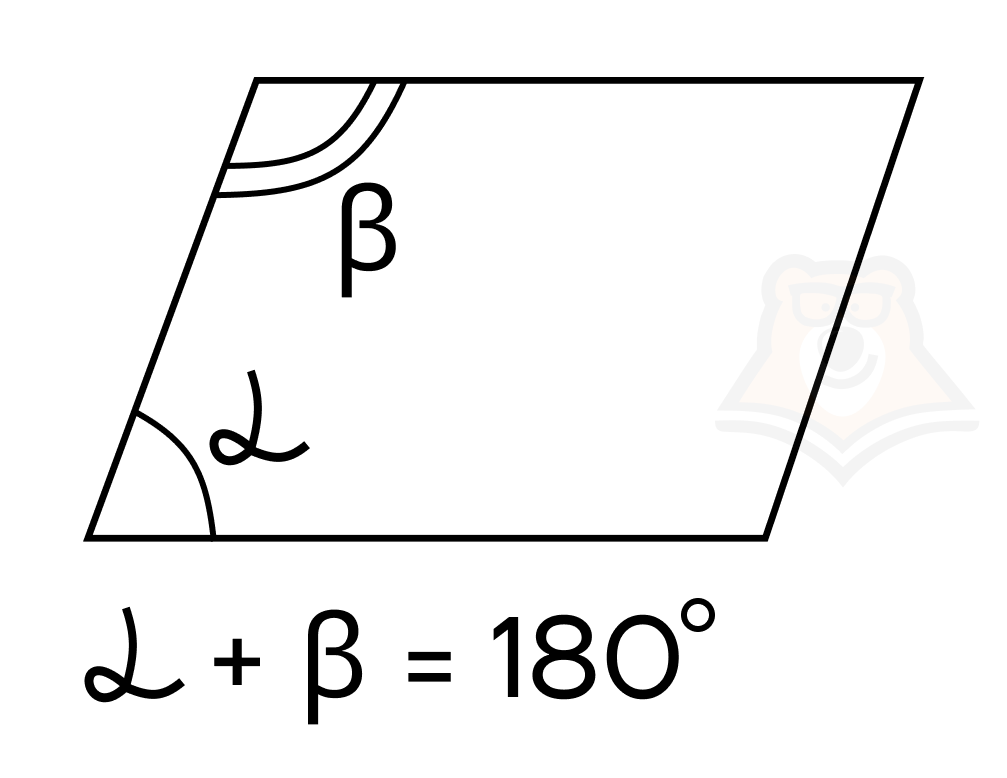
4) Сумма углов прилежащих к любой стороне равна 180°.
Это так, потому что, как в примере на картинке, стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 180°.
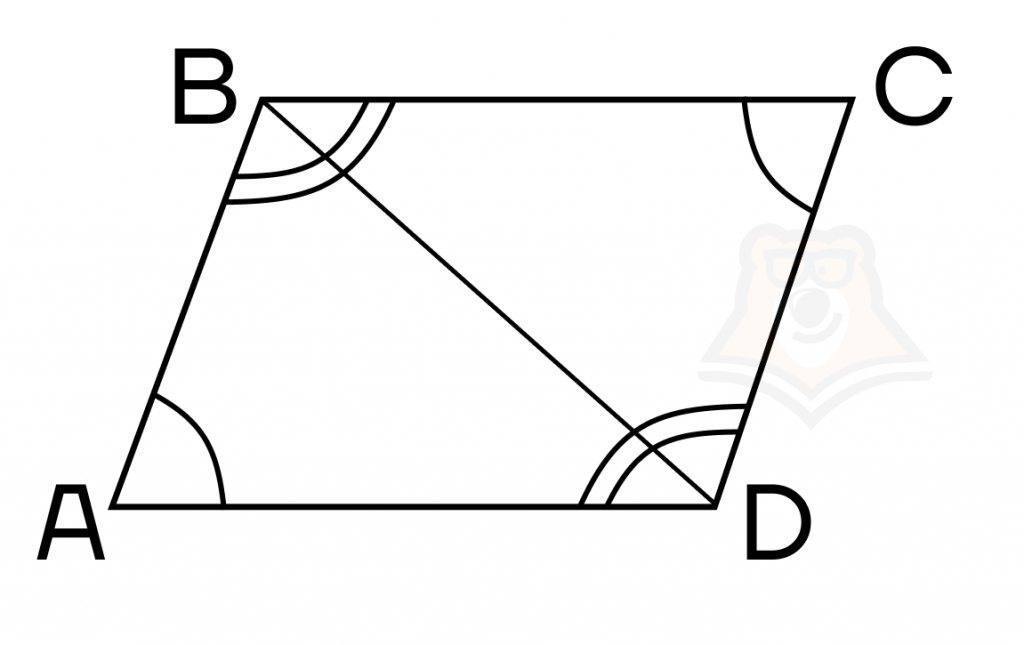
5) Противолежащие углы попарно равны. Это доказывается через третий признак равенства треугольников, ведь, например, у треугольников ABD и BDC все стороны равны, а значит и углы тоже.
Теперь перейдем к признакам параллелограмма. Это то, что нам помогает понять, что четырехугольник является параллелограммом.
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма
- Две противоположные стороны четырехугольника параллельны и равны.
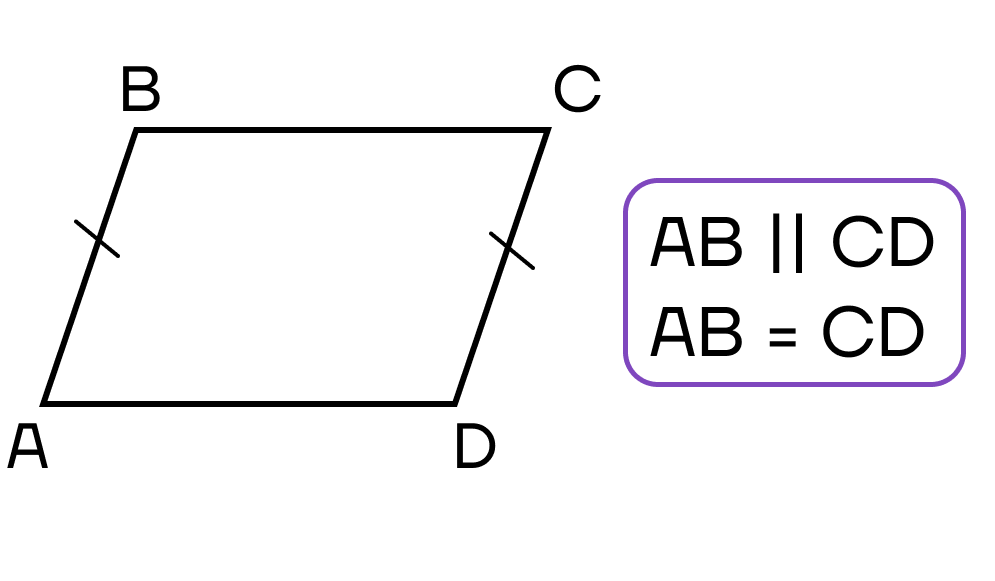
- Противоположные стороны четырехугольника попарно равны.
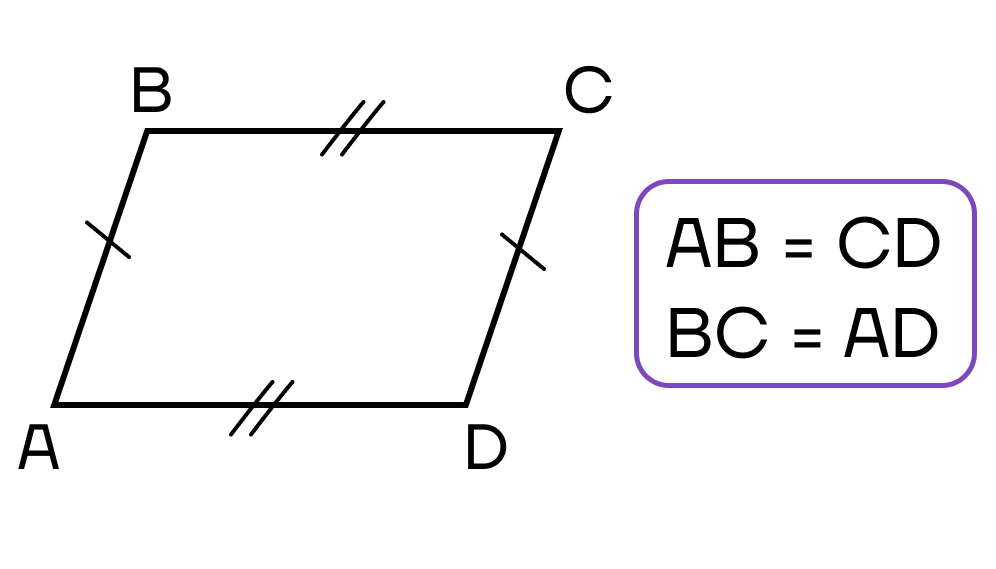
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.
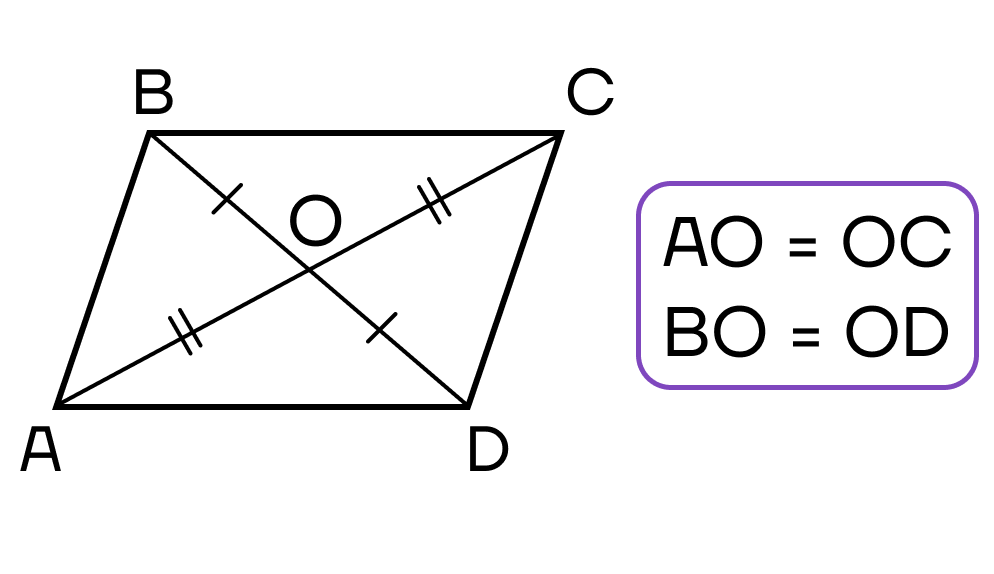
Теперь рассмотрим биссектрису в параллелограмме.
Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.
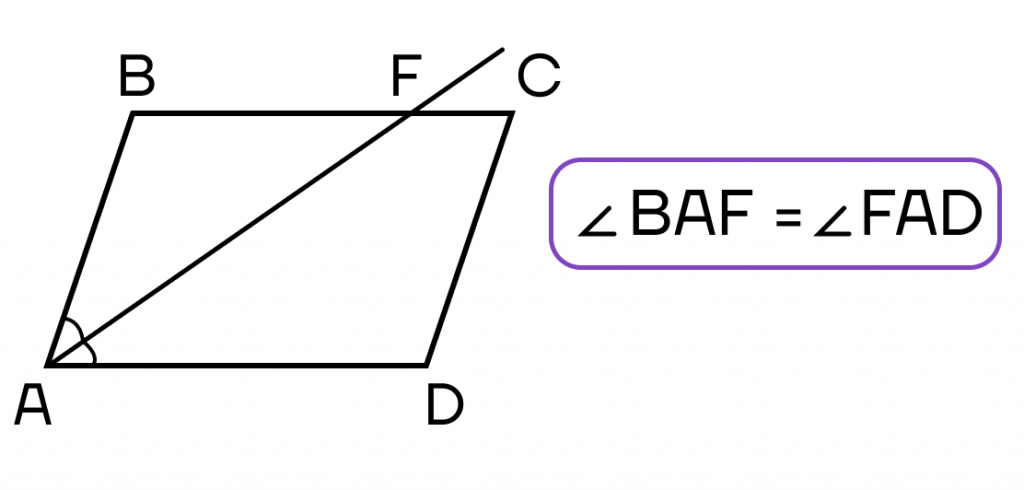
Рассмотрим два полезных факта, связанных с биссектрисой в параллелограмме.
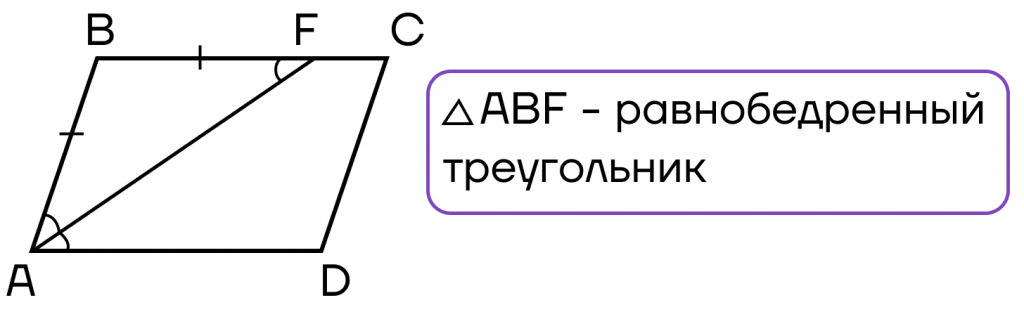
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.
Это тоже доказывается с помощью параллельных прямых. Рассмотрим две параллельные прямые: AD и BC, а также секущую AF. Углы FAD и BFA равны, так как они накрест лежащие. А так как AF — биссектриса, то углы BAF и FAD, углы FAD и BFA тоже, значит и BAF = BFA. Следовательно, треугольник BAF — равнобедренный.
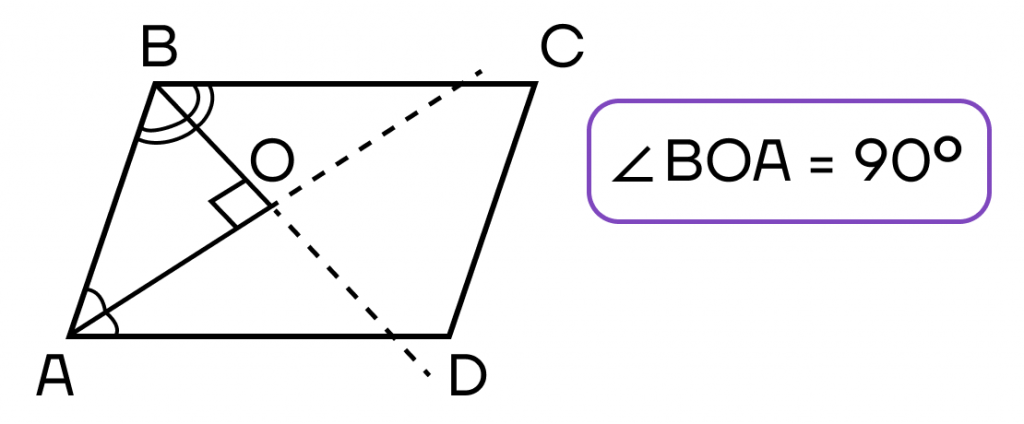
- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
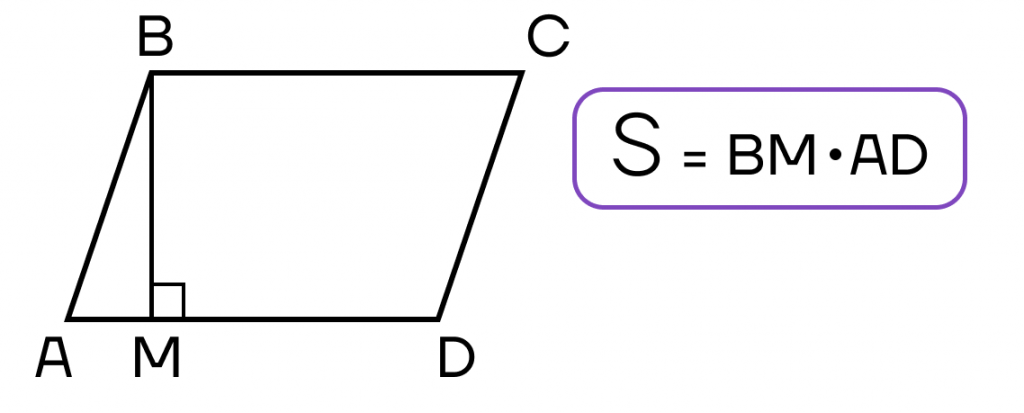
Мы почти закончили изучение параллелограмма. Осталось только рассмотреть формулы для нахождения площади. Их всего три.
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
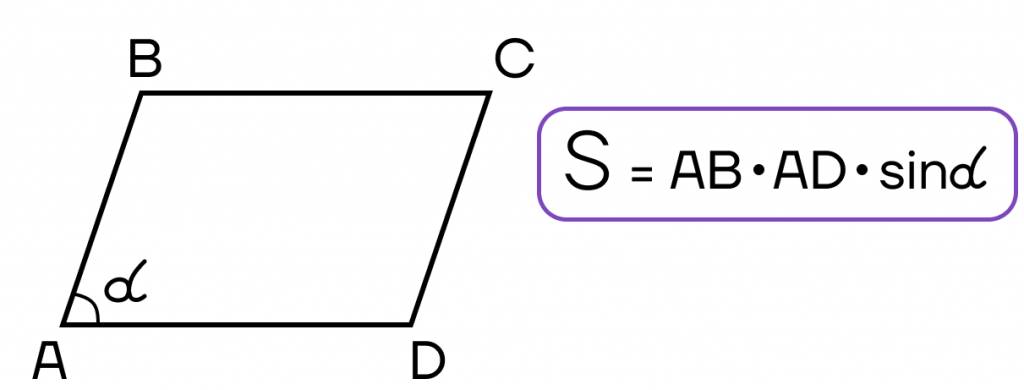
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.
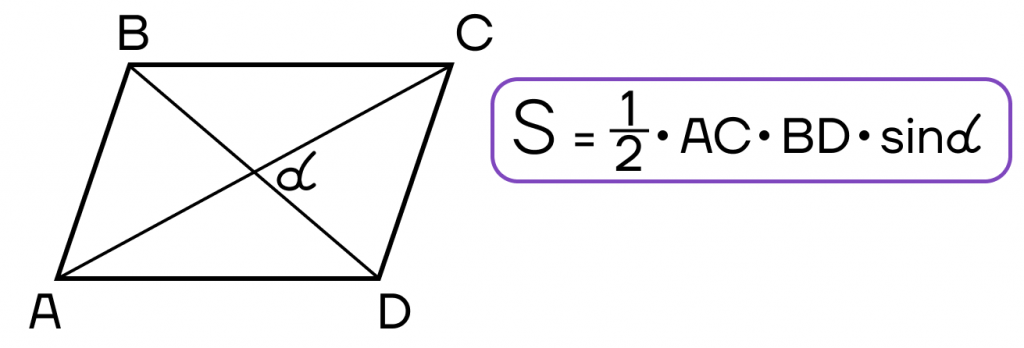
Какая фигура является антагонистом параллелограмма?Есть такая фигура, которая называется «антипараллелограмм». Это плоский и самопересекающийся четырехугольник, в котором две противоположные стороны равны между собой, но не параллельны. Напомним, что у параллелограмма противоположные стороны равны и параллельны между собой.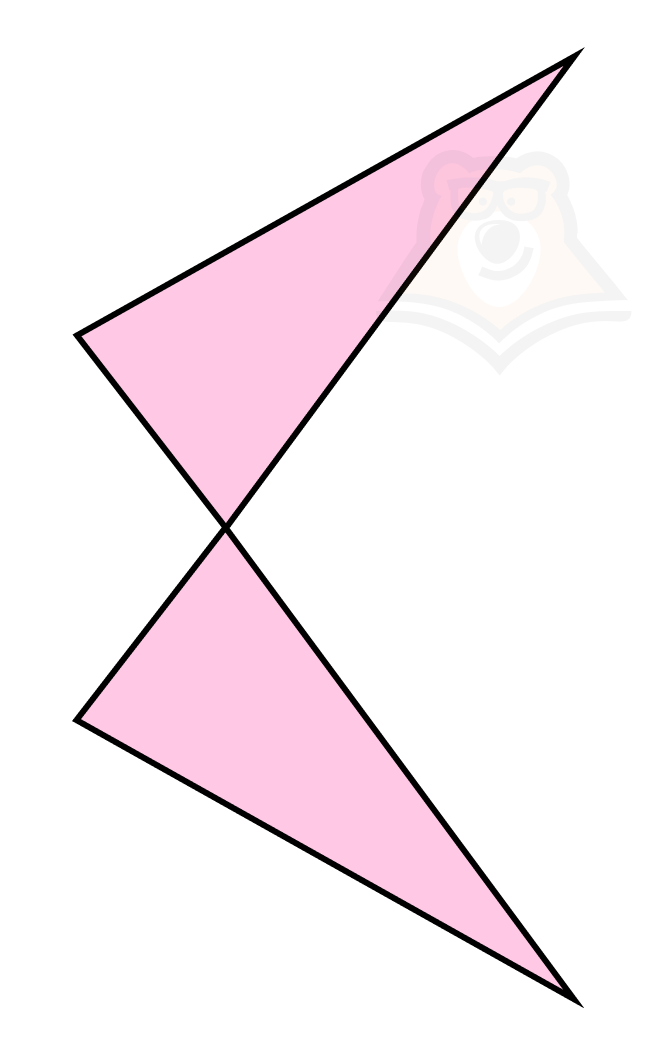 |
Мы рассмотрели всю теорию, связанную с параллелограммом. Давайте теперь решим задание для закрепления материала.
Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Стороны параллелограмма равны 10 и 15. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.
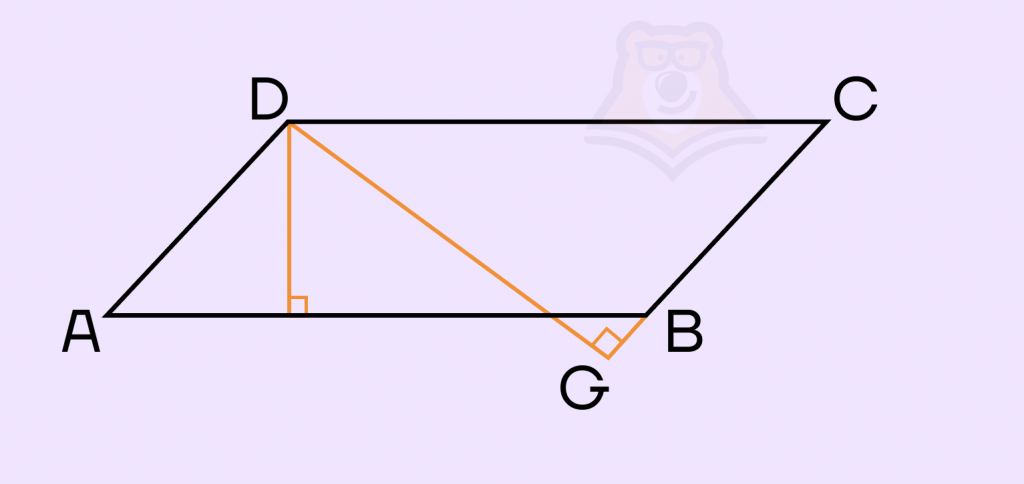
Решение. Примем искомую высоту за x. Как мы уже знаем, площадь параллелограмма можно найти с помощью высоты и стороны, к которой эта высота проведена. Соответственно, с помощью этой формулы мы и можем найти x:\(S = a*h_1=b*h_2\)\(S=10*12=15*h_2\)\(h_2=\frac{10*12}{15}\)\(h_2=8\)Ответ: 8
На этом мы закончили изучение параллелограмма, так что можем двигаться дальше!
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный шкафчик.


Конспект урока «Прямоугольник. Свойство его сторон. Квадрат»
-Здравствуйте, мои дорогие дети! Сегодня мои друзья и помощники плюс и минус заняты очень важным делом. Присоединяйтесь к нашему турниру по поиску неисправностей. И нам необходимо знакомиться с новыми темами. Поэтому я решил объяснить вам это сам. Но прежде чем мы начнем, я прошу вас отгадать загадку.
У двери, за столом, в книге.
О какой фигуре мы сегодня говорим? Вы уже поняли, что речь идет о прямоугольниках.
Теперь внимательно посмотрите на экран. Что вы видите на экране?
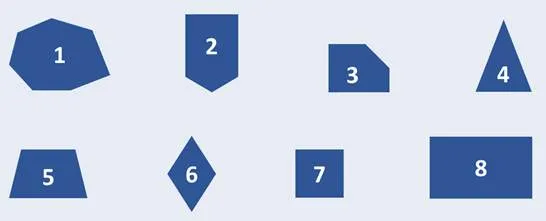
Конечно, эти фигуры можно назвать одним словом — многоугольники. Существуют фигуры с тремя углами, четырьмя углами, пятью углами и т.д.
Вы уже знакомы с темой углов. И помните, что углы бывают разные — прямые, тупые, острые.
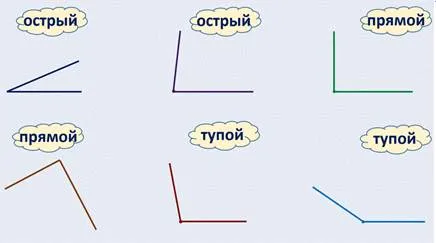
А фигура, о которой мы сегодня поговорим, называется прямоугольником. Вы слышите это? Прямой угол. Если мы скажем, что это прямоугольник, то вы догадаетесь, что это означает, что у него прямой угол.
Посмотрите на наш план. Затем с помощью линейки посмотрите, какая фигура находится под прямым углом. Посмотрите на первую диаграмму.
Это шестиугольник. Давайте проверим его углы.
Как видите, эта фигура имеет прямой угол, а остальные фигуры — непрямые.
Посмотрите на вторую диаграмму: это пятиугольник.
У него два прямых угла, остальные три — непрямые.
Третий также является пятиугольником. У него три прямых угла. Четвертый — треугольник. Пятый — это стол.
Эти фигуры не имеют правильных углов.
Но седьмой и восьмой:.
Все эти фигуры имеют правильные углы.
Такие фигуры с прямыми углами называются прямоугольниками
Обратите внимание, что обе фигуры с правильными углами являются четырехугольниками, т.е. имеют четыре угла и четыре стороны
Конечно, существуют различные четырехугольники. Однако прямоугольник называется четырехугольником только в том случае, если все углы правильные.
А теперь я предлагаю вам познакомиться с интересными свойствами прямоугольника. Вам понадобятся линейка и компас.
Перед нами прямоугольник. Посчитайте верхнюю часть.
Она равна 6 см. Затем измеряется нижняя часть, т.е. сторона, противоположная верхней части. Поэтому она называется другой стороной и также равна 6 см.
Они составляют 2 см. Рассчитайте другую сторону. Они также составляют 2 см. Следовательно, равны ли противоположные стороны прямоугольника? Или это только прямоугольник. Проверьте другой прямоугольник.
Стороны равны и противоположные стороны равны.
Теперь мы можем с абсолютной уверенностью сказать, что у прямоугольника равные стороны. Поэтому, называя длины сторон прямоугольника, не обязательно называть каждую сторону. Одна длинная сторона и только одна сторона может быть подписана. Ведь вы знаете, что противоположные стороны прямоугольника равны. Поэтому, подписав одну из сторон, вы знаете, что другая сторона этого прямоугольника также будет такой же длины.
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
Здесь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе.
Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие.
Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.
1) Площади четырехугольников
Площадь параллелограмма
произведение основания на высоту
пороизведение сторон на синус угла между ними
полупроизведение диагоналей на синус угла между ними
Площадь трапеции
произведение полусуммы оснований на высоту
произведение средней линии на высоту
полупроизведение диагоналей на синус угла между ними
Площадь произвольного четырехугольника
Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними
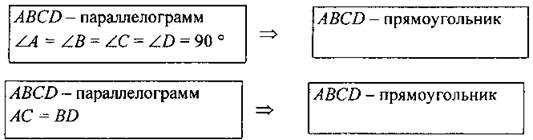
- 2) Свойства параллелограмма
-
В параллелограмме:
противолежащие стороны и углы равны - диагонали пересекаются и в точке пересечения делятся пополам
- 3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть
-
3) Cредняя линия в трапеции
Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и - 4) Средняя линия в равнобедренной трапеции
- Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
- То есть
- 5) Теорема с сдвиге диагонали в трапеции
- Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
- трапеция — равнобедренная равнобедренный
- 6) Четыре замечательные точки в трапеции
- Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
- То есть точки M, N, K и P лежат на одной прямой
Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан.
Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список.
Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией.
В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.
Колпаков Александр Николаевич. Репетитор по математике.
Как описать четырехугольник окружностью?
Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.
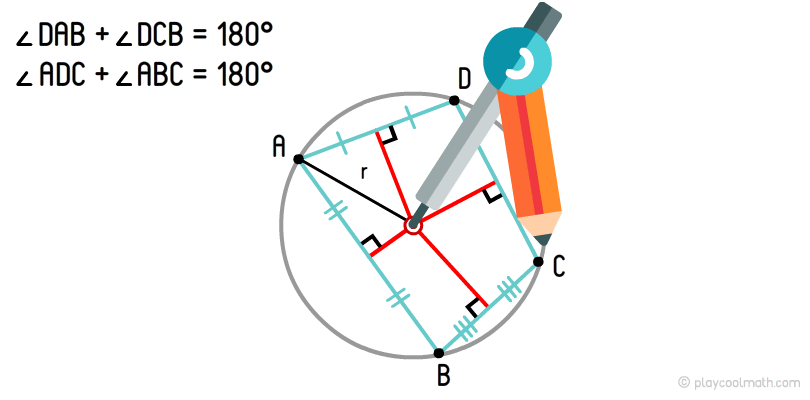 Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.
Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.
Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.
Найди ортодиагональные четырехугольники. 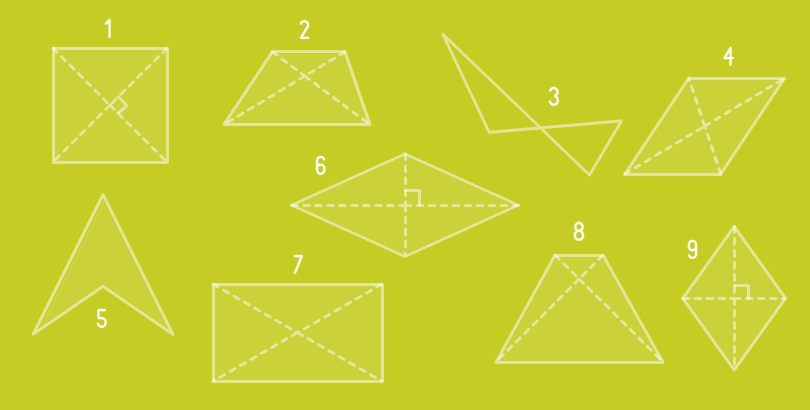
- #1
- #6
- #9
Основные свойства четырехугольников
Сумма углов четырехугольника
Перед тем как углубляться в сложные свойства, давайте вспомним базовое: сумма углов любого четырехугольника равна 360 градусов. Это означает, что если вы сложите значения всех углов четырехугольника, вы получите 360 градусов.
Практический эксперимент:
- Возьмите лист бумаги и нарисуйте любой четырехугольник.
- Используя транспортир, измерьте каждый угол и запишите его величину.
- Сложите все четыре значения. Результат должен быть равен 360 градусам!
Диагонали четырехугольника
Диагональ — это линия, соединяющая две несмежные вершины четырехугольника. В интересном факте, у четырехугольника может быть две диагонали!
Пошаговое рисование диагоналей:
- Нарисуйте на листе бумаги четырехугольник.
- Выберите одну из его вершин и проведите линию к противоположной вершине. Это первая диагональ.
- Теперь проведите линию от оставшейся вершины к ее противоположной. Это вторая диагональ.
- У вас на руках четырехугольник с двумя диагоналями!
Преимущества использования прямоугольников в геометрии
Когда дело доходит до геометрии, четырехугольники являются одними из самых захватывающих форм для изучения.Одним из самых популярных типов четырехсторонности является прямоугольник.Прямоугольники увлекательны из -за их уникальных свойств и преимуществ, которые они предлагают в области математики.От их симметрии до того факта, что их стороны перпендикулярны друг другу, прямоугольники предлагают несколько преимуществ, когда речь идет о решении проблем в мире геометрии.
Вот некоторые из преимуществ использования прямоугольников в геометрии:
1. простота расчета: прямоугольники относительно просты в расчете, что делает их идеальными для решения сложных задач.Поскольку все стороны перпендикулярны друг другу, легко найти площадь, периметр и другие измерения прямоугольника.
2. Симметрия: одним из самых захватывающих свойств прямоугольников является их симметрия.Это делает их идеальными для использования в дизайне и архитектуре, где часто ищут симметрию.Симметрия прямоугольника также позволяет легко делиться на меньшие формы или секции, что может быть полезно при решении более сложных задач.
3. Использование в повседневной жизни: прямоугольники повсюду в нашей повседневной жизни, от экранов, которые мы используем для просмотра фильмов до зданий, в которых мы живем и работаем. Понимание свойств прямоугольников может помочь нам понять мирвокруг нас и как это было построено.
4. параллельные стороны: Другое преимущество прямоугольников заключается в том, что их противоположные стороны параллельны.Это полезно при расчете длины диагонали или других измерений, которые включают параллельные линии.
Прямоугольники предлагают несколько преимуществ, когда дело доходит до решения проблем в области геометрии.От их простоты расчета до их симметрии и использования в повседневной жизни прямоугольники — это захватывающие формы, которые предлагают много понимания мира вокруг нас.
Преимущества использования прямоугольников в геометрии — четырехугольник: углубление в мир прямоугольников как четырехугольника
Страницы
- Главная страница
- 1. Натуральные числа
- 2. Точка. Прямая. Плоскость
- 3,4 Запись натуральных чисел. Классы в записи числа
- 5. Отрезок
- 6. Сравнение натуральных чисел
- 7. Луч
- 8, 9. Координатный луч
- 10, 11 Округление натуральных чисел
- 12, 13 Сложение натуральных чисел
- 14, 15, 16. Угол
- 17. Вычитание натуральных чисел
- 18. Ломаная
- 19, 20. Задачи на нахождение чисел по их сумме и разности
- 21, 22. Множества
- 23, 24, 25. Уравнения
- 26, 28. Обобщение по теме «Сложение и вычитание натуральных чисел»
- 29, 30, 31. Умножение натуральных чисел
- 32, 33. Степень числа с натуральным показателем
- 34, 35. Прямоугольник. Квадрат
- 36, 37, 38. Распределительный закон умножения
- 40. Деление натуральных чисел
- 41, 42. Задачи на нахождение двух чисел по их сумме и частному
- 43, 44. Задачи на нахождение чисел по их разности и частному
- 45, 46. Числовые выражения
- 47, 48, 49. Выражения с переменными
- 50, 51. Задачи на части
- 52. Обобщение по теме «Умножение и деление натуральных чисел»
- 56, 57. Делители и кратные
- 58. Признаки делимости на 2 и 4
- 59. Признаки делимости на 5 и 10
- 60, 61. Задачи на нахождение общих элементов множеств
- 62, 63. Деление с остатком
- 64, 65. Признаки делимости на 3 и на 9
- 66, 67. Прямоугольный параллелепипед. Куб
- 68, 69. Объем параллелепипеда
- 70, 71, 72. Задачи на движение
- 73, 74, 75. Задачи на движение по воде
- 76. Простые и составные числа
- 77, 78. Разложение числа на простые множители
- 79. Шкалы
- 80, 81. Измерение углов
- 82, 83. Общие делители. Взаимно простые числа
- 84, 85. Наибольший общий делитель
- 86, 87. Наименьшее общее кратное
- 88. Перпендикулярные и параллельные прямые
- 89, 90. Формулы
- 93, 94, 95. Задачи на нахождение элементов множест…
- 96, 97. Понятие дроби
- 98, 99. Дробь как частное от деления натуральных чисел
- 100. Какую часть одно число составляет от другого
- 101, 102. Нахождение части (дроби) от числа
- 103, 104. Нахождение числа по его части (дроби)
- 105, 106. Основное свойство дроби
- 107, 108. Сокращение дроби
- 109, 110. Приведение дробей к общему знаменателю
- 111, 112. Сравнение дробей
- Задания по теме «Дроби»
- 113, 114. Правильные и неправильные дроби
- 115, 116, Сложение дробей с одинаковыми знаменателями
- 117-120. Сложение дробей с разными знаменателями
- 121, 122. Законы сложения дробей
- 123, 124. Вычитание дробей с одинаковыми знаменателями
- 125, 126, 127. Вычитание дробей с разными знаменателями
- 131, 132. Умножение дробей
- 133, 134. Законы умножения дробей
- 139, 140. Деление дробей
- 141, 142, 143. Часть (дробь) от числа
- 144, 145. Задачи на совместную работу
- 146, 147, 148. Обобщение по теме «Умножение и деление дробей»
- 149, 150. Смешанные дроби
- 151, 152. Сравнение смешанных дробей
- 153, 154. Изображение дробей на координатном луче
- 155, 156. Сложение смешанных дробей
- 157, 158. Вычитание смешанных дробей
- 159, 160. Умножение и деление смешанных дробей
- 161, 162. Среднее арифметическое
- 163, 164, 165. Упражнения на все действия со смешанными дробями
- 166, 168. Обобщение «Смешанные дроби»
- 169, 170, 171. Повторение
Сумма внешних углов четырехугольника
Пусть задан четырехугольник \( \small A_1A_2A_3A_4 .\) Внешний угол при вершине \( \small A_1\) равен \( \small 180°-\angle A_1.\) Аналогично, внешние углы при вершинах \( \small A_2, \ A_3, \ A_4 \) равны \( \small 180°-\angle A_2, \) \( \small 180°-\angle A_3, \) \( \small 180°-\angle A_4, \) соответственно. Тогда сумма внешних углов четырехугольника равна:
Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.
Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB<AD+DC+CB.
Через вершины A и C проведем диагональ AC. Применим неравенство треугольника для треугольников ABC и ADC:
Подставляя (2) в (1), получим:
Геометрия 8 класс — Технологические карты уроков по учебнику Л. С. Атанасяна — 2015
ПРЯМОУГОЛЬНИК — ЧЕТЫРЕХУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для введения определения прямоугольника, изучения свойств прямоугольника |
||||
|
Термины и понятия |
Прямоугольник, диагонали прямоугольника |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач. Регулятивные: проявляют познавательный интерес к изучению предмета. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: умеют контролировать процесс и результат учебной математической деятельности |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
||||
|
I этап. Проверка домашнего задания |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Выявить трудности, возникшие при выполнении домашнего задания |
(И/Ф) 1. Сформулируйте теорему Фалеса. 2. Сформулируйте свойства равнобедренной трапеции. 3. Решите устно задачи по готовым чертежам. |
1. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 2. В равнобедренной трапеции углы при основаниях равны, диагонали равны. 3. ∆ABC — равнобедренный. ∠BAC = ∠BCA = х°, как внутренние накрест лежащие при ВС || AD и секущей АС,∠BAD = ∠CDA = 2х°. Из прямоугольного ∆ACD: ∠CAD + ∠CDA = 90° => х = 30°. В трапеции ABCD ∠BAC = ∠CAD = 60°, ∠BCD = 120° |
|||
|
II этап. Изучение нового материала |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Ввести понятие прямоугольника, доказать свойства и признаки прямоугольника |
1. Ввести понятие прямоугольника. Учащиеся знакомы с прямоугольником еще с начальной школы, поэтому ввести понятие прямоугольника можно в процессе беседы по вопросам: — Какой четырехугольник называется прямоугольником? (Ученики могут дать различные ответы, например: “Это четырехугольник, у которого все углы прямые”; “Это четырехугольник, у которого противолежащие стороны равны”.) — Можно ли утверждать, что прямоугольник — это параллелограмм, и почему? — Чем отличается произвольный параллелограмм от прямоугольника? — Закончите предложение: “Прямоугольник — это параллелограмм, у которого…” — Сформулируйте свойства прямоугольника. (И/Г) 2. Рассмотреть особое свойство диагоналей прямоугольника. — Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу. |
||||
|
Параллелограмм |
Прямоугольник |
||||
|
Стороны |
1. 2. |
1. 2. |
|||
|
Углы |
1. 2. |
1. 2. 3. |
|||
|
Диагонали |
1. |
1. 2. |
|||
|
(И/Ф) 3. Рассмотреть признак прямоугольника. — Как определить, является ли данный параллелограмм прямоугольником? Ответ обоснуйте. (Дать учащимся 3-5 минут на обдумывание и обсудить варианты ответов.) (Ф) — Выберите верные утверждения (устно): а) Если в четырехугольнике диагонали равны и делятся точкой пересечения пополам, то этот четырехугольник — прямоугольник. б) Если в четырехугольнике противоположные стороны параллельны, а все его углы прямые, то этот четырехугольник — прямоугольник. в) Если в четырехугольнике диагонали равны, то этот четырехугольник — прямоугольник. г) Если в параллелограмме два угла прямых, то этот параллелограмм — прямоугольник. д) Если в четырехугольнике два прямых угла и две стороны равны, то этот четырехугольник — прямоугольник. е) Если в четырехугольнике диагонали равны, а один угол прямой, то этот четырехугольник — прямоугольник |
|||||
|
III этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Совершенствовать навыки решения задач, опираясь на полученные знания |
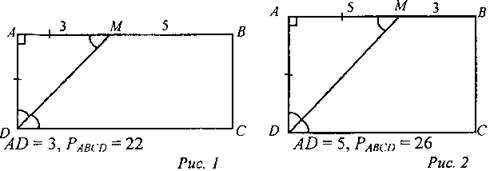
(И/Ф)1. Решите задачу: В прямоугольнике ABCD биссектриса угла D пересекает сторону АВ в точке М. Докажите, что ∆ADM — равнобедренный. Найдите периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной 3 см и 5 см. Сколько решений имеет задача? 2. Решите № 403. Дано: ABCD — прямоугольник, АС ∩ BD = О, ∠CAD = 30°, АС = 12 см. Найти: РAOB |
1. Решение:
№ 403. Решение: ∆ACD — прямоугольный, в нем ∠CAD = 30°, значит, тогда АВ = CD = 6 см. В прямоугольнике диагонали равны и точкой пересечения делятся пополам, то есть РAOB = АО + ВО + АВ = 6 + 6 + 6 = 18 см. Ответ: РАOB = 18 см |
|||
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф)
|
(И) Домашнее задание: п. 46 прочитать, решить № 401, 404 |
ПредыдущаяСледующая
Важность перпендикулярных сторон в прямоугольниках
В прямоугольнике перпендикулярные стороны играют решающую роль в определении уникальной формы четырехсторонней.Когда мы смотрим на прямоугольник, мы сразу же замечаем две пары сторон, которые являются конгруэнтными и параллельными друг с другом.Но именно перпендикулярные стороны придают прямоугольнику его отличительные прямые углы, которые необходимы для многих практических применений.От строительства до инженерии, архитектуры до математики, важность перпендикулярных сторон в прямоугольниках не может быть переоценена.В этом разделе мы углубимся в то, как эти стороны определяют прямоугольник и почему они так важны. 1
Определение прямоугольника: перпендикулярные стороны прямоугольника — это стороны, которые встречаются под прямым углом.Эти стороны также известны как «высота» и «ширина» прямоугольника.Высота — это сторона, которая перпендикулярна основанию, а ширина — это сторона, которая параллельна основанию.Вместе высота и ширина определяют форму прямоугольника, что делает его уникальным типом четырехугольника
1. Определение прямоугольника: перпендикулярные стороны прямоугольника — это стороны, которые встречаются под прямым углом.Эти стороны также известны как «высота» и «ширина» прямоугольника.Высота — это сторона, которая перпендикулярна основанию, а ширина — это сторона, которая параллельна основанию.Вместе высота и ширина определяют форму прямоугольника, что делает его уникальным типом четырехугольника.
2. Свойства перпендикулярных сторон: перпендикулярные стороны прямоугольника имеют несколько важных свойств, которые делают их полезными в различных контекстах.Например, они всегда равны по длине, что означает, что противоположные стороны прямоугольника совпадают.Это свойство позволяет легко рассчитать область и периметр прямоугольника, а также создавать различные формы, используя прямоугольники в качестве строительных блоков.
3
Приложения в реальном мире: важность перпендикулярных сторон в прямоугольниках очевидна во многих реальных приложениях.Например, в строительстве и технике прямоугольники часто используются в качестве основы для строительных фундаментов, стен и этажей.правильные углы, предоставленные перпендикулярными сторонами, позволяют легко создавать прямые линии и углы, которые необходимы для создания стабильных и сильных структур
4. Использование перпендикулярных сторон в математике: в математике перпендикулярные стороны играют решающую роль в геометрии, тригонометрии и исчислении.Они используются для определения фигур, рассчитывать области и объемы и решать различные уравнения и проблемы.Например, в тригонометрии перпендикулярные стороны правого треугольника используются для определения функций синуса, косинуса и касательной, которые необходимы для решения различных проблем в физике, инженерии и других областях.
Важность перпендикулярных сторон в прямоугольниках не может быть переоценена.Эти стороны определяют уникальную форму прямоугольника и необходимы для различных практических применений.От строительства до математики свойства и применение перпендикулярных сторон делают их важной концепцией для понимания. Важность перпендикулярных сторон в прямоугольниках — четырехугольник: углубление в мир прямоугольников как четырехугольника
Важность перпендикулярных сторон в прямоугольниках — четырехугольник: углубление в мир прямоугольников как четырехугольника
Особенности выпуклых и невыпуклых четырехугольников
Выпуклый четырехугольник
Свойства выпуклого четырехугольника:
- Все внутренние углы меньше 180 градусов.
- Две диагонали выпуклого четырехугольника лежат внутри него и не пересекают его стороны.
- Внутри выпуклого четырехугольника можно провести любую прямую, пересекающую две его стороны, и она будет целиком находиться внутри фигуры.
Невыпуклый четырехугольник
Особенности невыпуклых четырехугольников:
- У них есть хотя бы один внутренний угол, превышающий 180 градусов.
- Невыпуклый четырехугольник имеет диагонали, которые могут выходить за его границы.
- Невозможно провести прямую внутри невыпуклого четырехугольника так, чтобы она пересекала все его стороны и оставалась внутри фигуры.
Примеры доказательства
Доказательство прямоугольности четырехугольника может осуществляться на основании различных признаков. Ниже приведены несколько примеров доказательств:
1. Диагонали равны и перпендикулярны: Если в четырехугольнике диагонали равны между собой и перпендикулярны, то это является признаком его прямоугольности. Для доказательства этого признака можно воспользоваться теоремой о равенстве диагоналей параллелограмма или теоремой о четырехугольнике, у которого диагонали попарно равны и перпендикулярны.
2. Равенство длин сторон: Если в четырехугольнике все стороны равны между собой, то это также является признаком его прямоугольности. Для доказательства этого признака необходимо убедиться в равенстве всех сторон четырехугольника путем измерения и сравнения их длин.
3. Прямые углы: Если в четырехугольнике имеются два соседних угла, которые являются прямыми (равны 90 градусам), то это является признаком его прямоугольности. Для доказательства этого признака необходимо воспользоваться измерительными инструментами, такими как гониометр или угломер, для определения величины углов.
Это лишь несколько примеров доказательства прямоугольности четырехугольника. В каждом конкретном случае необходимо учитывать особенности фигуры и применять соответствующие методы доказательства.
В заключение: геометрия 8 класса и четырехугольники
В 8 классе российских школ особое внимание уделяется геометрии. Изучение четырехугольников играет важную роль в формировании геометрических навыков у учащихся
- Понимание свойств: В 8 классе ученики углубляются в изучение свойств различных четырехугольников, что помогает им в дальнейшем решать более сложные задачи.
- Практические задачи: Учащиеся решают разнообразные задачи, связанные с четырехугольниками, что помогает закрепить теоретические знания на практике.
- Подготовка к ЕГЭ: Знание основных свойств четырехугольников и умение работать с ними – это важная часть подготовки к единому государственному экзамену по математике.
Знание геометрии формирует логическое мышление и аналитические способности, которые пригодятся учащимся в будущем независимо от выбранной ими профессии.