Графическое представление двенадцатиугольника и его углов
Чтобы нарисовать графическое представление двенадцатиугольника, можно начать с круга. Разделите круг на двенадцать равных долей, деля его на двенадцать угловых секторов. Каждый угловой сектор будет соответствовать одной стороне двенадцатиугольника.
Угловая величина каждого сектора в двенадцатиугольнике составляет 360 градусов, поделенных на 12, что равно 30 градусам. Таким образом, каждый угол в двенадцатиугольнике равен 30 градусам.
Используя данную информацию, можно создать графическое представление двенадцатиугольника, обозначив его стороны и углы. Например, можно построить диаграмму, в которой каждая сторона двенадцатиугольника будет представлена линией, а каждый угол будет обозначен точкой с указанием его величины (30 градусов).
Такое графическое представление поможет лучше понять форму и структуру двенадцатиугольника, а также его углы. Оно позволит визуализировать свойства и особенности этого многоугольника.
Сумма углов выпуклого десятиугольника
Таким образом, сумма углов в десятиугольнике равна (10-2) * 180 = 1440 градусов. Это значит, что если измерить каждый угол в десятиугольнике и сложить их значения, получится именно 1440 градусов.
Сумма углов в десятиугольнике всегда будет постоянной величиной. Даже если углы десятиугольника не равны между собой, их сумма всегда будет составлять 1440 градусов. Это является одним из свойств выпуклых многоугольников и может быть использовано при решении геометрических задач или в расчетах.
Знание суммы углов в десятиугольнике может быть полезно при изучении геометрии или при решении практических задач. Например, если известны значения некоторых углов в десятиугольнике, можно использовать их для определения значений других углов.
Сумма углов выпуклых многоугольников
Сумма внутренних углов выпуклого многоугольника устанавливается по формуле:
где n — число вершин n-угольника.
Сумма углов выпуклого многоугольника вычисляется довольно просто. Рассмотрим любую такую геометрическую фигуру. Для определения суммы углов внутри выпуклого многоугольника необходимо соединить одну из его вершин с другими вершинами. В результате такого действия получается (n-2) треугольника. Известно, что сумма углов любых треугольников всегда равна 180°. Поскольку их количество в любом многоугольнике равняется (n-2), сумма внутренних углов такой фигуры равняется 180° х (n-2).
Сумма углов выпуклого многоугольника, а именно любых двух внутренних и смежных с ними внешних углов, у данной выпуклой геометрической фигуры всегда будет равна 180°. Исходя из этого, можно определить сумму всех ее углов:
Сумма внутренних углов составляет 180° * (n-2). Исходя из этого, сумму всех внешних углов данной фигуры устанавливают по формуле:
180° * n-180°-(n-2)= 360°.
Сумма внешних углов любого выпуклого многоугольника всегда будет равна 360° (независимо от количества его сторон).
Внешний угол выпуклого многоугольника в общем случае представляется разностью между 180° и величиной внутреннего угла.
Как найти периметр многоугольника и определить диагонали
Периметром многоугольника называется сумма длин его сторон.
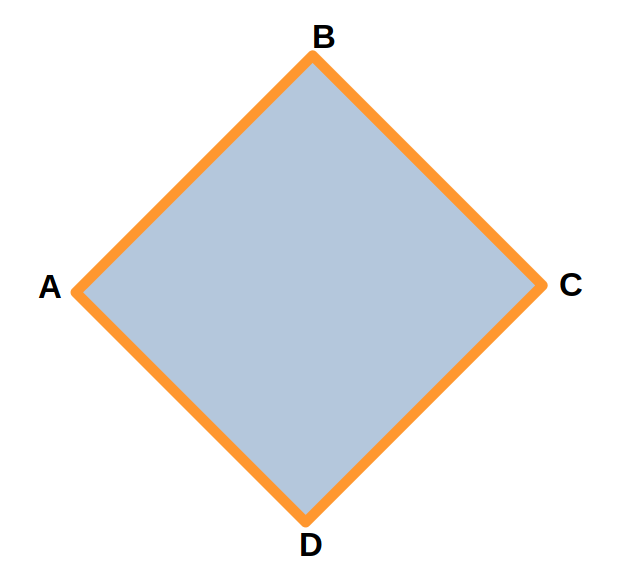
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.
Пример
Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти периметр четырехугольника.
Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см
Ответ: периметр четырехугольника ABCD равен 12 см.
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.
Например, отрезок AD будет являться диагональю фигуры ABCDEF:
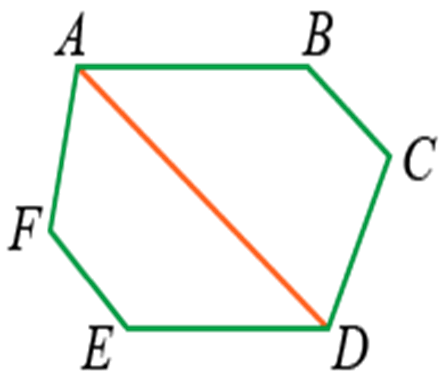
Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:
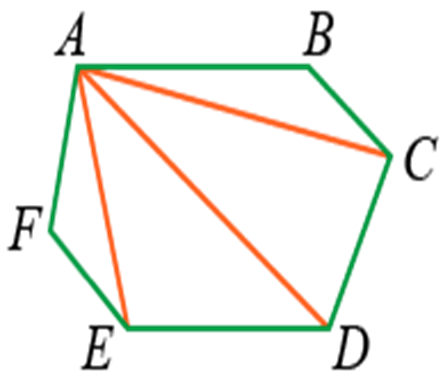
Количество треугольников будет на 2 меньше, чем число сторон:
Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.
Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.
Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.
Определение многоугольника
Многоугольники делятся на разные типы в зависимости от количества сторон. Наиболее известными многоугольниками являются треугольник, четырехугольник (квадрат, прямоугольник, ромб и т.д.), пятиугольник (пятиугольник, пентагон), шестиугольник (шестиугольник, гексагон) и так далее.
Чтобы найти сумму углов многоугольника, надо знать только число вершин n. Для любого n-угольника сумма всех его углов равна (n-2) * 180 градусов.
Пример:
Для десятиугольника сумма углов будет (10-2) * 180 = 1440 градусов.
Таким образом, сумма углов многоугольника равна (n-2) * 180 градусов, где n — количество вершин многоугольника.
Сумма углов многоугольника
В основном курсе геометрии доказывается, что сумма углов выпуклого n-угольника равна 180° (n-2). Оказывается, что это утверждение справедливо и для невыпуклых многоугольников.
Теорема 3. Сумма углов произвольного n-угольника равна 180° (n – 2).
Доказательство. Разобьем многоугольник на треугольники, проведением диагоналей (рис. 11). Число таких треугольников равно n-2, и в каждом треугольнике сумма углов равна 180°. Поскольку углы треугольников составляют углы многоугольника, то сумма углов многоугольника равна 180° (n – 2).
Рассмотрим теперь произвольные замкнутые ломаные, возможно с самопересечениями A1A2…AnA1 (рис. 12, а). Такие самопересекающиеся ломаные будем называть звездчатыми многоугольниками (рис. 12, б-г).
Зафиксируем направление подсчета углов против часовой стрелки. Заметим, что углы, образованные замкнутой ломаной, зависят от направления ее обхода. Если направление обхода ломаной меняется на противоположное, то углами многоугольника будут углы, дополняющие углы исходного многоугольника до 360°.
Если M – многоугольник, образован простой замкнутой ломаной, проходимой в направлении по часовой стрелке (рис. 13, а), то сумма углов этого многоугольника будет равна 180° (n – 2). Если же ломаная проходится в направлении против часовой стрелки (рис. 13, б), то сумма углов будет равна 180° (n + 2).
Таким образом, общая формула суммы углов многоугольника, образованного простой замкнутой ломаной, имеет вид = 180° (n 2), где – сумма углов, n – число углов многоугольника, «+» или «-» берется в зависимости от направления обхода ломаной.
Наша задача состоит в том, чтобы вывести формулу суммы углов произвольного многоугольника, образованного замкнутой (возможно самопересекающейся) ломаной. Для этого введем понятие степени многоугольника.
Степенью многоугольника называется число оборотов, совершаемой точкой при полном последовательном обходе его сторон. Причем обороты, совершаемые в направлении против часовой стрелки, считаются со знаком «+», а обороты по часовой стрелке – со знаком «-».
Ясно, что у многоугольника, образованного простой замкнутой ломаной, степень равна +1 или -1 в зависимости от направления обхода. Степень ломаной на рисунке 12, а равна двум. Степень звездчатых семиугольников (рис. 12, в, г) равна соответственно двум и трем.
Аналогичным образом понятие степени определяется и для замкнутых кривых на плоскости. Например, степень кривой, изображенной на рисунке 14 равна двум.
Для нахождения степени многоугольника или кривой можно поступать следующим образом. Предположим, что, двигаясь по кривой (рис. 15, а), мы, начиная с какого-то места A1, совершили полный оборот, и попали в ту же точку A1. Удалим из кривой соответствующий участок и продолжим движение по оставшейся кривой (рис. 15,б). Если, начиная с какого-то места A2, мы снова совершили полный оборот и попали в ту же точку, то удаляем соответствующий участок кривой и продолжаем движение (рис. 15, в). Считая количество удаленных участков со знаками «+» или «-», в зависимости от их направления обхода, получим искомую степень кривой.
Теорема 4. Для произвольного многоугольника имеет место формула
где – сумма углов, n – число углов, m – степень многоугольника.
Доказательство. Пусть многоугольник M имеет степень m и условно изображен на рисунке 16. M1, …, Mk – простые замкнутые ломаные, проходя по которым, точка совершает полные обороты. A1, …, Ak – соответствующие точки самопересечения ломаной, не являющиеся ее вершинами. Обозначим число вершин многоугольника M, входящих в многоугольники M1, …, Mk через n1, …, nk соответственно. Поскольку, помимо вершин многоугольника M, к этим многоугольникам добавляются еще вершины A1, …, Ak, то число вершин многоугольников M1, …, Mk будет равно соответственно n1+1, …, nk+1. Тогда суммы их углов будут равны 180° (n1+12), …, 180° (nk+12). Плюс или минус берется в зависимости от направления обхода ломаных. Сумма углов многоугольника M0, оставшегося от многоугольника M после удаления многоугольников M1, …, Mk, равна 180° (n-n1- …-nk+k2). Суммы углов многоугольников M0, M1, …, Mk дают сумму углов многоугольника M и в каждой вершине A1, …, Ak дополнительно получим 360°. Следовательно, имеем равенство
180° (n1+12)+…+180° (nk+12)+180° (n-n1- …-nk+k2)=+360°k.
= 180° (n2…2) = 180° (n+2m),
где m – степень многоугольника M.
В качестве примера рассмотрим вычисление суммы углов пятиконечной звездочки (рис. 17, а). Степень соответствующей замкнутой ломаной равна -2. Поэтому искомая сумма углов равна 180.
Что такое двенадцатиугольник?
Каждый угол двенадцатиугольника обозначается символом α и измеряется в градусах (°). Сумма всех углов двенадцатиугольника может быть вычислена с помощью специальной формулы.
Формула для вычисления суммы углов двенадцатиугольника:
Сумма углов двенадцатиугольника = (12 — 2) × 180° = 1800°
Это означает, что все углы двенадцатиугольника в сумме дают 1800 градусов.
Двенадцатиугольник может иметь различные формы и размеры, но у него всегда будет двенадцать сторон и двенадцать углов. Он может быть правильным (у всех сторон и углов одинаковая длина и мера) или неправильным (различные стороны и углы).
Двенадцатиугольники широко используются в геометрии и математике для решения различных задач и в качестве примеров для изучения свойств многоугольников.
Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
a6 = R
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах
Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности
Использование тригонометрии для расчета суммы углов двенадцатиугольника
Двенадцатиугольник представляет собой многоугольник с двенадцатью углами и двенадцатью сторонами. Для расчета суммы углов этого двенадцатиугольника можно использовать тригонометрические соотношения.
Сумма углов двенадцатиугольника вычисляется по формуле:
| Сумма углов | = | (12 — 2) * 180° |
| = | 10 * 180° | |
| = | 1800° |
Таким образом, сумма углов двенадцатиугольника равна 1800°. Это значит, что если мы сложим все углы двенадцатиугольника, получим именно такую величину.
Использование тригонометрии позволяет упростить расчеты суммы углов многоугольников, таких как двенадцатиугольник. Зная формулы и принципы тригонометрии, можно быстро и точно рассчитать суммы углов многоугольников различного размера и количества углов.
Сумма внешних углов выпуклого многоугольника
Зададимся теперь вопросом: «Чему равна сумма внешних углов выпуклого многоугольника?» Ответить на этот вопрос можно следующим образом. Каждый внешний угол является смежным с соответствующим внутренним. Поэтому он равен :
Тогда сумма всех внешних углов равна . То есть она равна .
То есть получается весьма забавный результат. Если отложить последовательно друг за другом все внешние углы любого выпуклого n-угольника, то в результате заполнится ровно вся плоскости.
Этот интересный факт можно проиллюстрировать следующим образом. Давайте пропорциональном уменьшать все стороны какого-нибудь выпуклого многоугольника до тех пор, пока он не сольётся в точку. После того, как это произойдёт, все внешние углы окажутся отложенными один от другого и заполнят таким образом всю плоскость.
Интересный факт, не правда ли? И таких фактов в геометрии очень много. Так что учите геометрию, дорогие школьники!
Материал о том, чему равна сумма углов выпуклого многоугольника, подготовил , Сергей Валерьевич
Сумма углов n-угольника Теорема. Сумма углов выпуклого n-угольника равна 180 o (n-2). Доказательство. Из какой-нибудь вершины выпуклого n-угольника проведем все его диагонали. Тогда n-угольник разобьется на n-2 треугольника. В каждом треугольнике сумма углов равна 180 о, и эти углы составляют углы n-угольника. Следовательно, сумма углов n- угольника равна 180 о (n-2).
Второй способ доказательства Теорема. Сумма углов выпуклого n-угольника равна 180 o (n-2). Доказательство 2. Пусть O какая-нибудь внутренняя точка выпуклого n-угольника A 1 …A n. Соединим ее с вершинами этого многоугольника. Тогда n-угольник разобьется на n треугольников. В каждом треугольнике сумма углов равна 180 о. Эти углы составляют углы n-угольника и еще 360 о. Следовательно, сумма углов n- угольника равна 180 о (n-2).
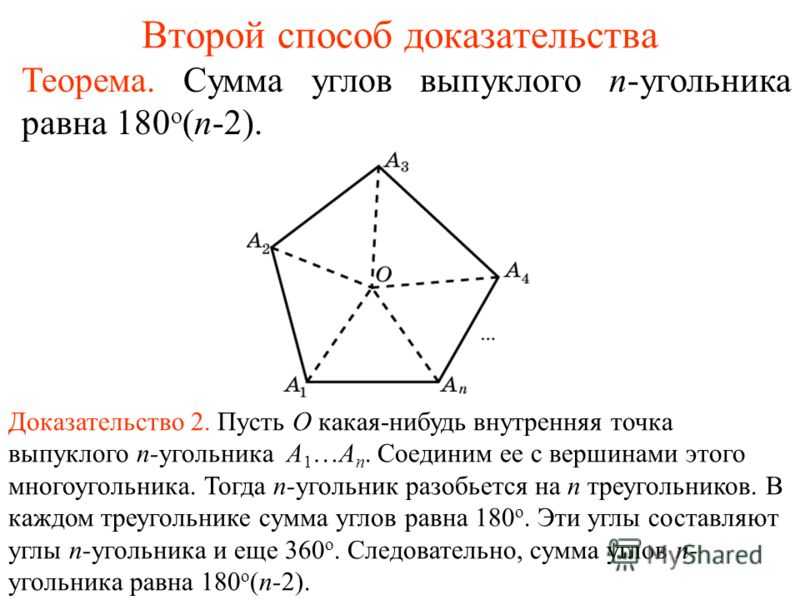


Упражнение 3 Докажите, что сумма внешних углов выпуклого n- угольника равна 360 о. Доказательство. Внешний угол выпуклого многоугольника равен 180 о минус соответствующий внутренний угол. Следовательно, сумма внешних углов выпуклого n-угольника равна 180 о n минус сумма внутренних углов. Так как сумма внутренних углов выпуклого n-угольника равна 180 о (n-2), то сумма внешних углов будет равна 180 о n о (n-2) = 360 о.
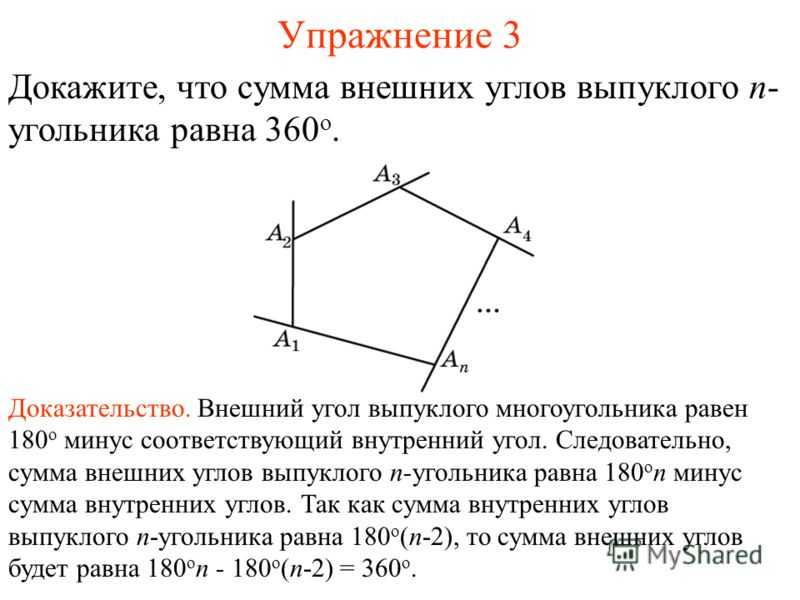
Упражнение 4 Чему равны углы правильного: а) треугольника; б) четырехугольника; в) пятиугольника; г) шестиугольника; д) восьмиугольника; е) десятиугольника; ж) двенадцатиугольника? Ответ: а) 60 о;б) 90 о;в) 108 о;г) 120 о; д) 135 о;е) 144 о;ж) 150 о.
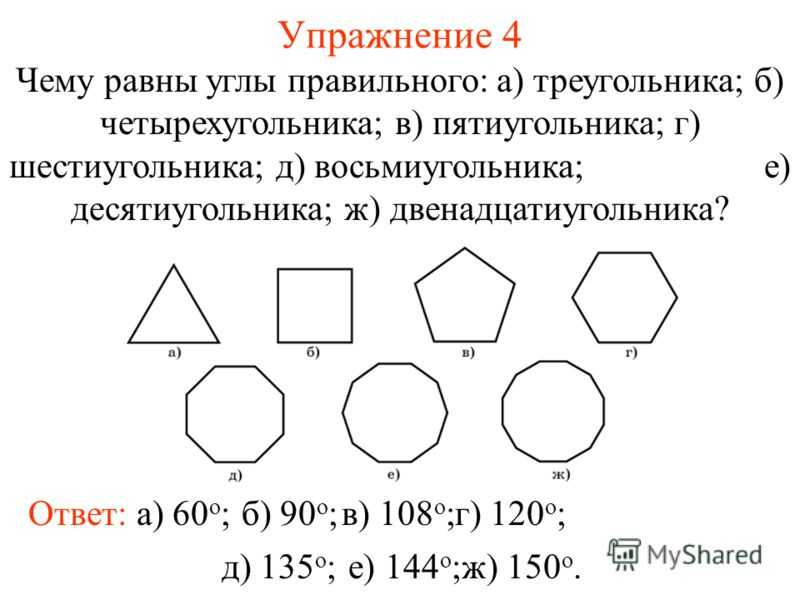


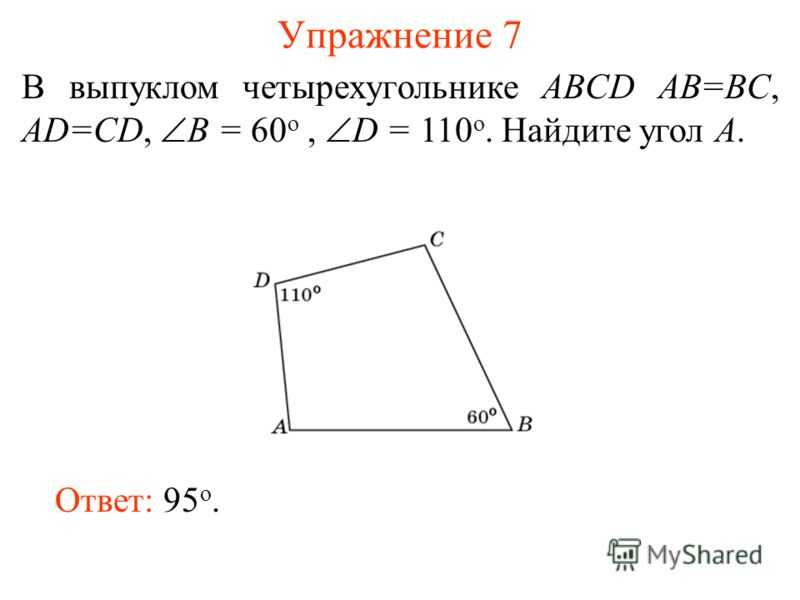


Упражнение 12* Какое наибольшее число острых углов может иметь выпуклый n-угольник? Решение. Так как сумма внешних углов выпуклого многоугольника равны 360 о, то у выпуклого многоугольника не может быть более трех тупых углов, следовательно, у него не может быть более трех внутренних острых углов. Ответ. 3.

Видеоурок 2:
Многоугольники. Решение задач
Лекция:
Многоугольник. Сумма углов выпуклого многоугольника
Многоугольники
– это фигуры, которые окружают нас везде – это и форма сот, в которых пчелы хранят свой мед, архитектурные сооружения, а так же многое другое.
Как уже говорилось ранее, многоугольники – это фигуры, у которых больше двух углов. Они состоять из замкнутой ломаной линии.
Причем углы многоугольников могут быть наружные и внутренние. Например, звезда – это фигура, которая имеет 10 углов, при этом некоторые из них выпуклые, а другие вогнутые:
Примеры выпуклых многоугольников:
Обратите внимание, на рисунке показаны правильные многоугольники – именно такие подробно изучаются в школьном курсе математики. У любого многоугольника количество вершин совпадает с количеством сторон
Так же обратите внимание, что соседними вершинами называются те, которые имеют одну общую сторону. Например, у треугольника все вершины соседние
У любого многоугольника количество вершин совпадает с количеством сторон
Так же обратите внимание, что соседними вершинами называются те, которые имеют одну общую сторону. Например, у треугольника все вершины соседние
Чем больше углов у правильного многоугольника, тем больше их градусная мера. Однако, градусная мера угла выпуклого многоугольника не может быть больше или равной 180 градусам.
Чтобы определить общую градусную меру многоугольника, необходимо воспользоваться формулой.
Важность понимания суммы углов выпуклого двенадцатиугольника
Понимание суммы углов выпуклого двенадцатиугольника имеет важное значение при решении геометрических задач и проблем. Знание этой информации позволяет определить свойства и характеристики двенадцатиугольников, а также использовать их в различных приложениях
Сумма углов выпуклого двенадцатиугольника равна 1800 градусов. Это означает, что если просуммировать все углы двенадцатиугольника, получится именно это значение. Такое свойство позволяет легко определить величину каждого угла в двенадцатиугольнике, если известны другие углы.
Знание суммы углов двенадцатиугольника полезно при решении задач по построению фигур, определению угловых отношений и вычислению площадей. Например, если известны только некоторые углы двенадцатиугольника, можно использовать сумму углов для определения остальных углов и свойств фигуры.
Кроме того, понимание суммы углов выпуклого двенадцатиугольника необходимо для работы со сходными фигурами, такими как многоугольники большего количества сторон. Зная сумму углов двенадцатиугольника, можно легко расширить эти знания и применить их к другим многоугольникам.
Таким образом, понимание суммы углов выпуклого двенадцатиугольника является важным элементом геометрического анализа и решения задач. Это знание позволяет легче работать с данной фигурой и применять его в различных приложениях и ситуациях.
Углы выпуклых геометрических фигур
Углы выпуклого многоугольника — это углы, что образованы его сторонами. Внутренние углы находятся во внутренней области данной геометрической фигуры. Угол, что образован его сторонами, которые сходятся в одной вершине, называют углом выпуклого многоугольника. с внутренними углами данной геометрической фигуры, называют внешними. Каждый угол выпуклого многоугольника, расположенный внутри него, равен:
где х — величина внешнего угла. Эта простая формула действует в отношении любых геометрических фигур такого типа.
В общем случае, для внешних углов существует следующие правило: каждый угол выпуклого многоугольника равен разности между 180° и величиной внутреннего угла. Он может иметь значения в пределах от -180° до 180°. Следовательно, когда внутренний угол составляет 120°, внешний будет иметь величину в 60°.
Свойства выпуклого многоугольника
У выпуклого многоугольника все углы меньше $180^\circ$.
Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Докажем первое свойство
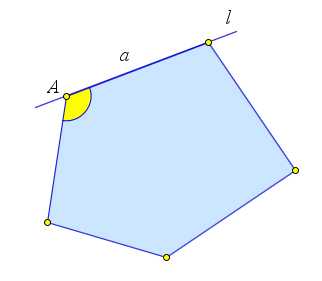
Возьмем любой угол $A$ выпуклого многоугольника $P$ и его сторону $a$, идущую из вершины $A$. Пусть $l$ – прямая, содержащая сторону $a$. Так как многоугольник $P$ выпуклый, то он лежит по одну сторону от прямой $l$. Следовательно, и его угол $A$ лежит по одну сторону от этой прямой. Значит угол $A$ меньше развернутого угла, то есть меньше $180^\circ$.
Докажем второе свойство
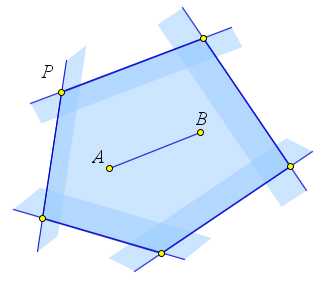
Возьмем любые две точки $A$ и $B$ выпуклого многоугольника $P$. Многоугольник $P$ является пересечением нескольких полуплоскостей. Отрезок $AB$ содержится в каждой из этих полуплоскостей. Поэтому он содержится и в многоугольнике $P$.
Сумма внутренних углов выпуклого многоугольника
| Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника. |
Как доказать эту формулу?
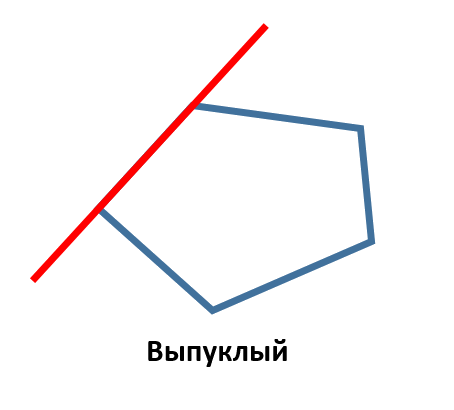
Прежде чем перейти к доказательству этого утверждения, вспомним, какой многоугольник называется выпуклым. Выпуклым называется такой многоугольник, который целиком находится по одну сторону от прямой, содержащей любую его сторону. Например такой, который изображен на этом рисунке:
Если же многоугольник не удовлетворяет указанному условию, то он называется невыпуклым. Например, такой:
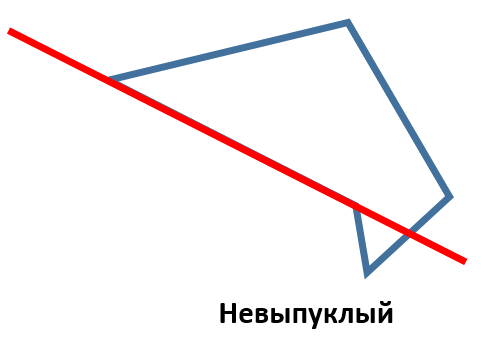
Сумма внутренних углов выпуклого многоугольника равна , где — количество сторон многоугольника.
Доказательство этого факта основано на хорошо известной всем школьникам теореме о сумме углов в треугольнике. Уверен, что и вам эта теорема знакома. Сумма внутренних углов треугольника равна .
Идея состоит в том, чтобы разбить выпуклый многоугольник на несколько треугольников. Сделать это можно разными способами. В зависимости от того, какой способ мы выберем, доказательства будут немного отличаться.
1. Разобьём выпуклый многоугольник на треугольники всеми возможными диагоналями, проведёнными из какой-нибудь вершины. Легко понять, что тогда наш n-угольник разобьётся на треугольника:
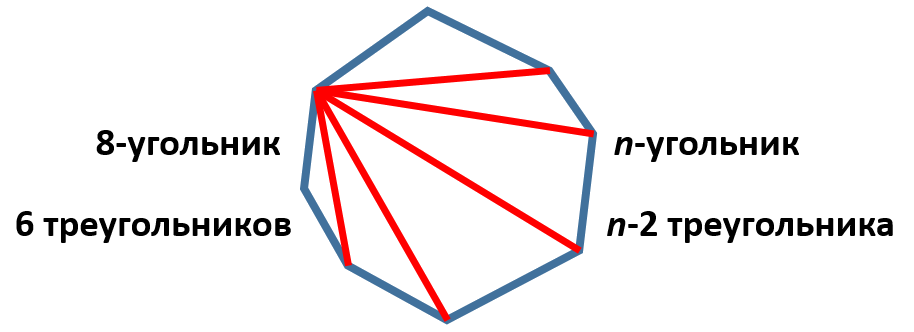
Причём сумма всех углов всех получившихся треугольников равна сумме углов нашего n-угольника. Ведь каждый угол в получившихся треугольниках является частичной какого-то угла в нашем выпуклом многоугольнике. То есть искомая сумма равна .
2. Можно также выбрать точку внутри выпуклого многоугольника и соединить её со всеми вершинами. Тогда наш n-угольник разобьется на треугольников:
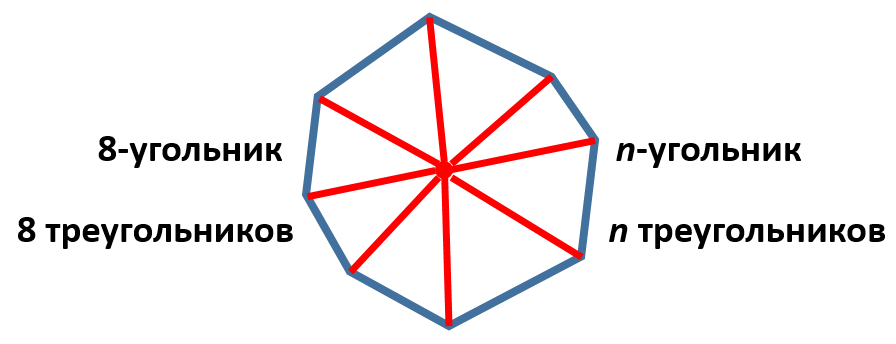
Причём сумма углов нашего многоугольника в этом случае будет равна сумме всех углов всех этих треугольников за вычетом центрального угла, который равен . То есть искомая сумма опять же равна .






























