индикатор Маха
Инженеры изо всех сил старались внедрять инновации, чтобы у пилота было меньше работы, le pusieron un piloto automático y casi no hacía nada, entonces los dueños de las aerolíneas le dijeron a los que hacían los aviones: “oigan, пónganles el trabajo de los navegantes ya que estos manes(пилоты) они больше ничего не делают” (ya les habían puesto parte del trabajo que hacían los radio- операторы, haciendo los equipos de radio máс жácil de usar; и если, las radio-ayudas les dieron la estocada final a los navegantes. Теперь с GPS. y navegación por satélite, quien sabe quién sea el siguiente. Мы уже знаем, что должность бортинженера (con tanta automatizacióн) нетó a mejor vida. Los dueños de las empresas creen que su empleado no hace lo suficiente y cada vez que los ingenieros hacen un avance y quitan un tripulante, они прыгают от счастья (на один союз меньше) и зарплата меньше платить. Скоро мы увидим пассажирские самолеты с одним пилотом.
El indicador mach que relacionaba la velocidad verdadera con la velocidad local del sonido y le decía al piloto la ground speed (Г.С.) не нужен калькулятор (если бы ветер был спокоен). Un avance notable para la época.
Realmente el indicador Mach en vuelos subsónicos te indicaba un porcentaje de la velocidad del sonido a esa altura. Например, если индикатор показывает .80 это означает, что вы идете в 80% от скорости звука на этой высоте, но ¿у.е.ál es esa velocidad del sonido?
¿Я имею в виду, что это для тебя? Потому что если это так, что вы не проедете на опасных скоростях (что они) Ставят индикатор на прибор (парикмахерская, который меняется в зависимости от факторов, влияющих на него) para que no llegues a él y no lo sobrepases, Адемás de ciertas alarmas que suenan cuando se exceden las velocidades críэтика.
Плюсы и минусы измерения скорости в махах
Плюсы:
1. Легкость и удобство: мах является широко используемой единицей измерения скорости в авиации и космической индустрии. Она позволяет быстро оценить и сравнить скорость движения объектов в атмосфере.
2. Относительность: мах позволяет измерять скорость относительно скорости звука, что особенно полезно при оценке скорости самолетов и ракет. Это позволяет определить, как быстро движется объект относительно звуковых волн и определить, насколько надзвуковым является его движение.
3. Проявление переходных явлений: измерение скорости в махах позволяет оценить, насколько близко объект подходит к скорости звука и какие переходные явления при этом происходят. Например, при движении относительно звуковой скорости возникает так называемый «ударный конус», который указывает на наличие ударной волны вокруг объекта.
Минусы:
1. Ограниченность применения: единица измерения в махах применима только в атмосфере, где скорость звука зависит от условий воздуха и может меняться. В вакууме или других средах, где звук не распространяется, махи не применимы.
2. Отсутствие абсолютности: значение маха зависит от условий окружающей среды, поэтому его нельзя однозначно перевести в другие единицы измерения скорости, такие как километры в час или узлы.
3. Запутанность понятий: мах часто путают с скоростью звука. Однако, скорость звука является постоянной величиной в определенных условиях, в то время как мах является относительной величиной и зависит от скорости звука в данной среде.
Измерение скорости в махах является удобным и наглядным способом оценки скорости движения объектов в атмосфере. Однако, необходимо помнить о его ограничениях и контексте, в котором применимы махи. В некоторых случаях может быть более удобным использование других единиц измерения скорости.
Общие сведения
 Поезд в движении. Железнодорожный вокзал в Симферополе, Крым, Россия.
Поезд в движении. Железнодорожный вокзал в Симферополе, Крым, Россия.
Скорость — мера измерения пройденного расстояния за определенное время. Скорость может быть скалярной величиной и векторной — при этом учитывается направление движения. Скорость движения по прямой линии называется линейной, а по окружности — угловой.
Измерение скорости
Среднюю скорость v находят, поделив общее пройденное расстояние ∆x на общее время ∆t: v = ∆x/∆t.
В системе СИ скорость измеряют в метрах в секунду. Широко используются также километры в час в метрической системе и мили в час в США и Великобритании. Когда кроме величины указано и направление, например 10 метров в секунду на север, то речь идет о векторной скорости.
Скорость движущихся с ускорением тел можно найти с помощью формул:
- Тело, движущееся с постоянным ускорением a, с начальной скоростью u в течении периода ∆t, имеет конечную скорость v = u + a×∆t.
- Тело, движущееся с постоянным ускорением a, с начальной скоростью u и конечной скоростью v, имеет среднюю скорость ∆v = (u + v)/2.
Число Маха в авиации
Теорию с подтверждающим экспериментальным процессом образования ударных волн был продемонстрировал еще задолго до первого полета сверхзвукового самолета австрийский физик Эрнст Мах (1838 — 1916). Величину, выражающую отношение скорости летательного аппарата к скорости звуковой волны называют сегодня в честь ученого — Махом.
Как мы уже оговорились в водной части, на скорость звука в воздушной среде влияют такие метеорологические условия как давление, влажность и температура воздуха. Температура в зависимости от высоты полета самолета меняется от +50 на поверхностях Земли до -50 в слоях стратосферы. Поэтому на разных высотах для достижения сверхзвуковых скоростей обязательно учитываются местные метеоусловия.
Для сравнения над нулевой отметкой уровня моря скорость звука составляет 1240 км/ч, тогда как на высоте более 13 тыс. км. эта скорость снижается до 1060 км/ч.
Если принять соотношение скорости летательного аппарата к скорости звукова за М, то при значении М>1, это будет всегда сверхсвуковая скорость.
Самолеты с дозвуковой скоростью имеют значение М = 0.8. Вилка значений Маха от 0,8 до 1,2 задают околозвуковую скорость. А вот гиперзвуковые летательные аппараты имеют число Маха более 5. Из известных военных российских сверхзвуковых самолетов можно выделить СУ-27 — истребитель перехватчик, Ту-22М — бомбардировщик ракетоносец. Из американских известен SR-71 — самолет разведчик. Первым сверхзвуковым самолетом в рамках серийного производства стал американский истребитель F-100 в 1953 году.
Модель космического челнока во время испытаний в сверхзвуковой аэродинамической трубе. Специальная методика теневой фотографии позволила запечатлеть, где возникают ударные волны.
Кто изобрел ракетное топливо?
Растет масса и сложность конструкции. Между тем, первое в мире однобаковое ракетное топливо изобрели, как они сами утверждают, китайцы. Называлось оно «черный порох». Боевые пороховые ракеты летают еще со времен средневековья, а в XX веке во всем мире развернулись работы по созданию ракет жидкостных.
На каком топливе работают спутники?
На каком топливе летают спутники? Гидразин — это летучее топливо, которое испортит вам день, а может быть и жизнь, если вы подвергнетесь его воздействию. Для заправки спутника вам понадобится много инфраструктуры безопасности, включая герметичные костюмы SCAPE на все тело, просто чтобы обращаться с этим материалом.
Как работают спутники на орбите?
Спутникам лететь бы по прямой линии, по инерции, но сила земного притяжения, как невидимая верёвка, изменяет направление их полёта, не даёт улететь от Земли. Спутники же летят на большой высоте, где почти нет воздуха, Поэтому они так долго вращаются вокруг Земли.
Как долго летают спутники?
Поэтому параметры орбиты выбраны так, что спутник появляется над обслуживаемой территорией в одно и то же время, совершая в течение суток два оборота вокруг Земли. Три спутника на разнесенных орбитах, запущенные с интервалом 8 часов, обеспечивают круглосуточную связь между любыми пунктами нашей страны.
Сколько стоит топливо для ракет?
По прайс-листу Российской компании, составные ракетного горючего, стоят: керосин ТС-1 – 44500 руб./тонна (36,05 руб./л); жидкий кислород – 9204 руб/т (9,2 руб./л); жидкий азот – 18500 руб./т (18,5 руб./л).
Сколько стоит 1 тонна авиационного керосина?
Средняя стоимость тонны авиакеросина в РФ в июле 2018 года выросла по сравнению с аналогичным периодом прошлого года на 18,2%, до 51,3 тысячи рублей, следует из статистики Росавиации. Так, в июле прошлого года тонна топлива марки ТС-1 стоила 43,4 тысячи рублей.
Сколько стоит 1 литр авиационного топлива?
Цены на керосин ТС 1
| Наименование | Цена, руб/литр |
|---|---|
| Керосин авиационный ТС-1 | 27,00 руб. |
Что такое Нафтил?
Нафтил – углеводородное слаботоксичное горючее, которое отличается от используемого в РН типа «Союза» топлива Т-1 относительно меньшим содержанием ароматических соединений.
Три, два, один — поехали
Число Маха в авиации (и не только) играет огромную роль. Практически все пилоты гражданских, военных и космических шаттлов не могут обойтись без него. Настолько важен этот параметр!
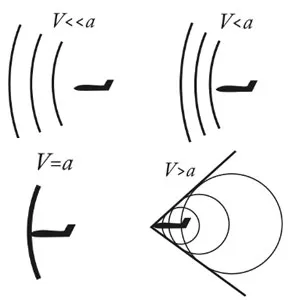
Когда летательный аппарат перемещается в пространстве, молекулы воздуха вокруг него начинают «возмущаться». Если скорость воздушного судна мала (M
На околозвуковой скорости (~1190 км/ч), малые возмущения передаются другим молекулам вокруг воздушного судна (проще рассматривать поверхность крыла), и в один прекрасный момент, когда в какой-то точке скорость набегающего потока сравнивается с местной скоростью звука (M=1, именно потока, ВС может лететь с меньшей скоростью), возникает ударная волна. Поэтому так очевидна разница в конструкции истребителей: их крылья, хвостовое оперение и фюзеляж, по сравнению с дозвуковыми летательными аппаратами.

На воздушных судах, выполняющих полеты с M
Для таких ВС в документах по летной эксплуатации (РЛЭ для отечественных, FCOM для зарубежных) указывается критическое число Маха. Это самое минимальное значение М, на котором набегающий поток в любой части воздушного судна достигнет скорости звука (Мкр). Вот и весь секрет!
Кстати, самые удачливые летающие пассажиры Советского Союза, путешествовали быстрее современных. Не верите?

Расчет
Когда скорость звука известна, число Маха, с которым летит самолет, можно рассчитать по формуле
- Мзнак равнотыс{\ displaystyle \ mathrm {M} = {\ frac {u} {c}}}
куда:
- М — число Маха
- u — скорость движущегося самолета и
- c — скорость звука на данной высоте (точнее температура)
а скорость звука зависит от термодинамической температуры как:
- сзнак равноγ⋅р*⋅Т,{\ displaystyle c = {\ sqrt {\ gamma \ cdot R_ {*} \ cdot T}},}
куда:
- γ{\ Displaystyle \ гамма \,}- отношение удельной теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (1,4 для воздуха)
- р*{\ Displaystyle R_ {*}}- удельная газовая постоянная для воздуха.
- Т,{\ Displaystyle Т,}- статическая температура воздуха.
Если скорость звука неизвестна, число Маха можно определить путем измерения различных давлений воздуха (статического и динамического) и использования следующей формулы, полученной из уравнения Бернулли для чисел Маха менее 1,0. Предполагая, что воздух является идеальным газом, формула для вычисления числа Маха в дозвуковом сжимаемом потоке:
- Мзнак равно2γ−1(дсп+1)γ−1γ−1{\ displaystyle \ mathrm {M} = {\ sqrt {{\ frac {2} {\ gamma -1}} \ left }} \,}
куда:
- q c – ударное давление (динамическое давление) и
- p — статическое давление
- γ{\ Displaystyle \ гамма \,}- отношение удельной теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (1,4 для воздуха)
- р*{\ Displaystyle R_ {*}}- удельная газовая постоянная для воздуха.
Формула для вычисления числа Маха в сверхзвуковом сжимаемом потоке выводится из сверхзвукового уравнения Пито Рэлея:
- птпзнак равноγ+12М2γγ−1⋅γ+11−γ+2γМ21γ−1{\ displaystyle {\ frac {p_ {t}} {p}} = \ left ^ {\ frac { \ gamma {\ gamma -1}} \ cdot \ left ^ {\ гидроразрыва {1} {\ гамма -1}}}
Расчет числа Маха по давлению в трубке Пито
Число Маха зависит от температуры и истинной воздушной скорости. Однако бортовые приборы для расчета числа Маха используют перепад давления, а не температуру.
Предполагая, что воздух является идеальным газом, формула для расчета числа Маха в дозвуковом сжимаемом потоке находится из уравнения Бернулли для M lt; 1 (выше):
- Мзнак равно5(дсп+1)27−1{\ Displaystyle \ mathrm {M} = {\ sqrt {5 \ влево }}\,}
Формулу для вычисления числа Маха в сверхзвуковом сжимаемом потоке можно найти из сверхзвукового уравнения Пито Рэлея (выше) с использованием параметров для воздуха:
- М≈0,88128485(дсп+1)(1−17М2)2,5{\ displaystyle \ mathrm {M} \ приблизительно 0,88128485 {\ sqrt {\ left ({\ frac {q_ {c}} {p}} + 1 \ right) \ left (1 — {\ frac {1} {7 \,\mathrm {M} ^{2}}}\справа)^{2.5}}}}
куда:
- q c — динамическое давление, измеренное за прямым скачком.
Как видно, M появляется в обеих частях уравнения, и для практических целей для численного решения необходимо использовать алгоритм нахождения корня (решение уравнения является корнем многочлена 7-го порядка по M 2 и, хотя некоторые из них могут быть решены явно, теорема Абеля-Руффини гарантирует, что не существует общей формы для корней этих многочленов). Сначала определяется, действительно ли M больше 1,0, путем вычисления M из дозвукового уравнения. Если в этой точке M больше 1,0, то значение M из дозвукового уравнения используется в качестве начального условия для итерации фиксированной точки сверхзвукового уравнения, которое обычно сходится очень быстро. В качестве альтернативы можно использовать метод Ньютона.
Скорость звука и ударная волна
Затемúmero Mach es la relación entre la velocidad verdadera y la velocidad local del sonido. Esta es una expresión adimensional de velocidad, какí que a una velocidad de Mach 1.0 переходит в местную скорость звука.Скорость звука на уровне моря равна 662 узлы (в воздухе). Маха 0.8 на уровне моря соответствует истинной скорости 528 узлов. (о Маха 0.8 равно 528 разрывается между 662 узлы). La velocidad del sonido en el aire decrece con la altitud por la disminución de la temperatura.
Aunque el avión vuele a velocidades subsónicas, в некоторых частях этого (особенно крыло) puede estar desplazando a velocidades supersónicas (как показано на рисунке 2) es ahí donde se produce la famosa onda de choque que destruye parte de la sustentacióн, crea una gran resistencia aerodinámica y además problemas de estabilidad. Es de ahí que nace el ala en flecha que realmente se usa para hacerle el “engaño del siglo” к относительному ветру на высоких скоростях
Todo esto tiene un gran valor para los diseñadores y constructores del avióн. Para el piloto es un conocimiento más de la máquina y de su desempeñо. ¿Cuál podría ser su utilidad adicional? En próximos capítulos podríamos hablar más afondo de esto (на языке, понятном любому любителю самолетов)
Скорость звука и число Маха
Когда заходит речь о сверхзвуковых или гиперзвуковых скоростях, вместо привычных большинству людей километров (или миль) в час начинают фигурировать какие-то странные «Махи». Например — «скорость самолета превысила 5,2 Маха». Что же это за единица измерения и как ее воспринимать?
Так называемое «число Маха» названо в честь Эрнста Маха, австрийского физика. Будучи одним из основоположников газовой механики и окончив жизнь в эпоху первых летающих «этажерок», «небесных тихоходов», он и подумать не мог, что уже в конце 1940-х гг. реактивные истребители вплотную приблизятся к звуковому барьеру, и единица скорости, названная его именем, войдет в повседневный обиход авиаторов.
Число Маха, или число М, как его также называют — не самая очевидная вещь для понимания. Одна из канонических трактовок звучит так: «отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде»… Впрочем, попробуем объяснить его понятными словами, «на пальцах».
Запредельно упрощенно (и весьма некорректно!) можно сказать, что единица числа Маха — это скорость звука. Иными словами, 1 Мах условно равен 340 метрам в секунду или 1224 км/ч. Соответственно, 2 Маха — условно 680 метров в секунду или 2448 км/ч, и далее соответственно. Однако любой преподаватель газодинамики за такое объяснение отвесит вам полновесного «леща» учебником Абрамовича. Ибо число Маха — это не скорость в классическом понимании — в виде расстояния, пройденного за отрезок времени. Эта безразмерная единица, хотя и плотно привязана к скорости звука в воздухе, учитывает тот факт, что скорость звука — вовсе не постоянная величина!
Чтобы преодолеть звуковой барьер непосредственно над землей, самолету нужно достичь скорости 1224 км/ч, а на высоте десяти тысяч метров для этого достаточно скорости 1076 км/ч — на 148 км/ч меньше. Разница около 13–14 процентов — это весьма немало и имеет существенное значение как для инженеров, проектирующих самолет, так и для пилотов, им управляющих. Иными словами, 1 Мах — это скорость звука при конкретных параметрах высоты и температуры, в которых летит самолет, «здесь и сейчас».
Обзор
Скорость звука (синий цвет) зависит только от изменения температуры на высоте (красный цвет) и может быть рассчитана исходя из него, поскольку изолированное влияние плотности и давления на скорость звука компенсирует друг друга. Скорость звука увеличивается с высотой в двух областях стратосферы и термосферы из-за тепловых эффектов в этих областях.
Число Маха является мерой характеристик сжимаемости потока жидкости : жидкость (воздух) ведет себя под влиянием сжимаемости аналогичным образом при заданном числе Маха, независимо от других переменных. Как смоделировано в Международной стандартной атмосфере , сухой воздух на среднем уровне моря , стандартная температура 15 ° C (59 ° F), скорость звука составляет 340,3 метра в секунду (1116,5 фута / с; 761,23 миль в час; 661,49 узлов). Скорость звука непостоянна; в газе она увеличивается пропорционально квадратному корню из абсолютной температуры , а поскольку атмосферная температура обычно снижается с увеличением высоты от уровня моря до 11 000 метров (36 089 футов), скорость звука также уменьшается. Например, в стандартной модели атмосферы температура снижается до -56,5 ° C (-69,7 ° F) на высоте 11 000 метров (36 089 футов) с соответствующей скоростью звука ( 1 Маха) 295,0 метров в секунду (967,8 футов / с; 659,9 миль в час; 573,4 узла), 86,7% от значения уровня моря.
Внешний вид в уравнении неразрывности
В качестве меры сжимаемости потока число Маха может быть получено из соответствующего масштабирования . Полное уравнение неразрывности для общего потока жидкости:
∂р∂т+∇⋅(рты)знак равно≡−1рДрДтзнак равно∇⋅ты{\ displaystyle {\ partial \ rho \ over {\ partial t}} + \ nabla \ cdot (\ rho {\ bf {u}}) = 0 \ эквив — {1 \ over {\ rho}} {D \ rho \over {Dt}}=\nabla \cdot {\bf {u}}}
производная по материалу , – плотность , – скорость потока . Для изоэнтропических изменений плотности, вызванных давлением, где скорость звука. Тогда уравнение неразрывности можно немного изменить, чтобы учесть это соотношение:ДДт{\ Displaystyle Д / Дт}р{\ Displaystyle \ ро}ты{\ displaystyle {\ bf {и}}}гпзнак равнос2гр{\ Displaystyle дп = с ^ {2} д \ ро}с{\ Displaystyle с}
−1рс2ДпДтзнак равно∇⋅ты{\ displaystyle — {1 \ over {\ rho c ^ {2}}} {Dp \ over {Dt}} = \ nabla \ cdot {\ bf {u}}}
Следующим шагом является обезразмеривание переменных как таковых:
Икс*знак равноИксл,т*знак равноUтл,ты*знак равнотыU,п*знак равно(п−п∞)рU2,р*знак равнорр{\ displaystyle {\ bf {x}} ^ {*} = {\ bf {x}} / L, \ quad t ^ {*} = Ut / L, \ quad {\ bf {u}} ^ {*} = {\ bf {u}} / U, \ quad p ^ {*} = (pp _ {\ infty}) / \ rho _ {0} U ^ {2}, \ quad \ rho ^ {*} = \ро /\ро _{0}}
где – характерный масштаб длины, – характерный масштаб скорости, – эталонное давление, – эталонная плотность. Тогда безразмерная форма уравнения неразрывности может быть записана как:л{\ Displaystyle L}U{\ Displaystyle U}п∞{\ Displaystyle р _ {\ infty}}р{\ Displaystyle \ ро _ {0}}
−U2с21р*Дп*Дт*знак равно∇*⋅ты*⟹−М21р*Дп*Дт*знак равно∇*⋅ты*{\ displaystyle — {U ^ {2} \ over {c ^ {2}}} {1 \ over {\ rho ^ {*}}} {Dp ^ {*} \ over {Dt ^ {*}}} = \nabla ^{*}\cdot {\bf {u}}^{*}\ подразумевает -{\text{M}}^{2}{1 \over {\rho ^{*}}}{Dp^{ *} \over {Dt^{*}}}=\nabla ^{*}\cdot {\bf {u}}^{*}}
где число Маха . В пределе уравнение неразрывности сводится к — это стандартное требование для течения несжимаемой жидкости
Разница между мах и другими единицами измерения скорости
В отличие от маха, километр в час (км/ч) является простой единицей измерения скорости, обозначающей расстояние, пройденное объектом за один час. Километр в час часто используется в повседневной жизни для измерения скорости автомобилей, самолетов и других средств передвижения.
Существует некоторая разница между махом и километром в час в том, что мах позволяет измерять относительную скорость объекта относительно скорости звука, а километр в час измеряет абсолютную скорость.
Например, если скорость объекта равна 768 км/ч, а скорость звука в данной среде равна примерно 1225 км/ч, то отношение скорости объекта к скорости звука будет составлять около 0,625 маха.
Еще одной единицей измерения скорости, используемой в аэронавтике, является узел (kt). Узел равен одной морской миле в час и часто используется для измерения скорости воздушных судов.
Интересно отметить, что скорость в махах может отличаться в разных средах. Например, скорость звука в воздухе составляет около 1225 км/ч, а в воде — около 1498 км/ч. Поэтому одна и та же скорость в махах будет иметь разные значения в разных средах.
В общем, мах и другие единицы измерения скорости, такие как километр в час и узел, предоставляют нам различные способы измерения скорости и являются важными при рассмотрении и сравнении скорости движения объектов.
GPS.ФМС
Se han inventado infinidad de sistemas de navegación cada vez mejor que el anterior, ahora ya puedes navegar por satélite y con un error de pocos metros, toda la información que necesites y (тот, который не) спагеттиén la puedes obtener en tiempo real, en tu propio teléfono inteligente y en el avióн, руководства, системы, контрольные списки и т.д.. ya no te puedes perderte nunca máс, la compañía dueña del avión te sigue el rastro, puedes enviar los problemas técnicos del avión mucho antes de aterrizar y todo lo que nunca nos imaginamos unas décadas atráс. Te subes al avióн, управляет с лету, Вы расслабляетесь и смотрите на пейзаж.
выводы
Al principio volábamos solo con la velocidad indicada y de ahí se tomaban todas las limitaciones, на малых высотах, это было очень близко к реальности, и так как все полеты были визуальными, no habíНинún problema. Мás tarde se empezó a volar más alto y máс рápido, ya no coincidían las velocidades y se tenían que hacer “complicados” сálculos para aproximarse a los vuelos por instrumentos (для дальних перелетов нужны были штурманы) так что инженеры (кто никогда не спит) они изобрели инструмент, который дал вам истинную скорость на инструменте, вам нужно было только расстояние DME и часы, чтобы сделать ваши оценки. Aun así, это было слишком много работы, y entonces esos “infames “ingenieros mejoraron los equipos y se inventaron los GPS que te daban la velocidad y la posición real, компонент ветра и оценка, просто ища нужную точку. Pero aun así no se conformaron y entonces te ponían todo en una gran pantalla, hasta el avión lo dibujaron en un mapa en tiempo real sobre una trayectoria a seguir, с учетом всего этого, ¿Не подскажете, для чего сегодня используется ваш индикатор MACH?, sabiendo que tienes además un indicador de IAS, что эквивалентно (для производительности и полетных ограничений) y que ya todos los datos del vuelo sobre navegación los tienes resueltos sobre un mapa en una pantalla?
В этой картине, entre muchas cosas máс, T.A.S говорит вам. (479) и Г.С.. (482) что означает, что у вас есть компонент попутного ветра 3 Узлы
постскриптум
я не пилот, я бортинженер, и летающая КАРАВЕЛЛА, un jet francéс, un capitán instructor, el Mayor JAIRO GARCIA me enseño todo esto que les estoy contando ahora, вторые пилоты и некоторые командиры (в épocas que no existía el G.P.S.) se sorprendían como les daba los tiempos para el descenso y los datos de combustibles exactos. По факту, Я не принижаю показатель Маха, Напротив, estoy manifestando que en una época era subutilizado por algunos aviadores que no lo entendían a cabalidad. Si algún piloto tiene algo que añadir, приветствую вклад.
Quiero agradecer la colaboración de Yerson Leonardo Angarita
Все чертежи и фотографии были получены от Boeing
Скорость звука
Скорость звука A определяется как скорость распространения малого возмущения (тип 1)
где DP — увеличение давления DP — увеличение плотности.
Поскольку процесс распространения малых возмущений можно считать изоэнтропийным (т.е. без теплообмена и потерь)
где ρ — давление в среде, н/м2, ρ — плотность среды, кг/м3, R — газовая постоянная, нм/кг 0 К, T — температура, 0 К. k — изотропный экспонент, преобразующий теплоемкость газа при постоянном давлении в теплоемкость при постоянном объеме, определяется
Производные dp/(p x ρ) этих уравнений определяются с учетом следующего соотношения

Если пренебречь влиянием производной dz / dT, то скорость звука определяется уравнением 2.
Значение скорости звука зависит от притока (или оттока) тепла или механической работы, так как температура газа T может меняться. Однако уравнения 1 и 2 остаются в силе для воздействия на газы, которые не вызывают химических реакций.
Конечно, это можно легко объяснить тем, что изменения плотности и волнового давления можно рассматривать как малые, но конечные величины, в то время как толщина волны δ настолько мала, что ее следует считать минутной.
Таким образом, сила массы, переходящая через звуковую волну, обеспечивает условия, которые на порядки больше, чем изменения плотности или давления.
Критическая скорость
Во многих случаях полезно использовать понятие критической скорости αx, которая относится к локальной скорости, равной скорости звука, вместе со скоростью звука.
Для определения критической скорости используется общее уравнение сохранения энергии

Уравнение критической скорости
где T* — критическая температура.
С другой стороны, скорость a* например, скорость звука, определяется следующими уравнениями.
Из последних двух уравнений имеем

Где. — скорость звука в неподвижной среде.
Поэтому скорость звука в воздухе

Число Маха
Скорость потока пропорциональна скорости звука, а в некоторых случаях даже быстрее.
В таких случаях важной характеристикой потока является отношение скорости потока к скорости звука. Формула для определения числа Маха выглядит следующим образом
Формула для определения числа Маха выглядит следующим образом
где w — скорость потока в среде, а α — скорость звука.
Число Маха является одним из основных критериев подобия потока для определения явлений сжимаемости. Известно, что при ультразвуковых скоростях свойства потока резко меняются.
Важность числа Маха заключается в том, что оно показывает, превышает ли скорость потока газообразной среды скорость звука. Действительно, если M > 1, это означает, что поток движется быстрее скорости звука
Действительно, если M > 1, это означает, что поток движется быстрее скорости звука.
Тогда, если M1 — ультразвуковой. Кроме того, это не все потоки жидкости.
Есть еще несколько. Как вы уже знаете, скорости от 1 до 5 Махов называются ультразвуковыми; от 5 до 23 Махов — ультразвуковыми 23 Маха и выше — первая космическая скорость.
Числа Маха являются безразмерными величинами, но для понимания их порядка во многих источниках приводятся в единицах системы СИ. Это означает, что число Маха должно быть в километрах в час.
В этом случае один Мах соответствует 1 199 км/ч или 333 м/с
Обратите внимание, однако, что эти значения достигаются при нормальном атмосферном давлении и нулевой температуре и влажности на поверхности почвы
Поскольку давление, температура и влажность изменяются на разных высотах от земли, меняется и скорость звука.
Так, например, для истребителя, летящего со скоростью 2,3 Маха или 2 450 км/ч на высоте 18 000 м над землей, 1 Мах будет равен 1065 км/ч или 295 м/с.
Историческая справка
Название число Маха
и обозначение М
предложил в 1929 году Якоб Аккерет (J.Ackeret). Ранее в литературе встречалось название число Берстоу
(Bairstow , обозначение
B
a
{\displaystyle {\mathsf {Ba}}}
), а в советской послевоенной научной литературе и, в частности, в советских учебниках 1950-х годов — название число Маиевского
(число Маха — Маиевского
) по имени основателя русской научной школы баллистики , пользовавшегося этой величиной, вместе с этим обозначение
M
{\displaystyle {\mathsf {M}}}
употребляется без специального названия , это частные проявления кампании «борьбы с космополитизмом» .


























