Виды систем отсчета

Относительность движения и система отсчета в физике

Относительность движения проявляется в том, что поведение движущегося тела может быть определено только по отношению к другому телу, так называемому телу отсчета.

Система отсчета выбирается произвольно

Обратите внимание, что движущееся тело и система отсчета — это одно и то же. Каждый из них может рассматриваться либо как система отсчета, либо как движущееся тело при расчете движения, если это необходимо

Например: человек стоит на земле и наблюдает за машиной, едущей по дороге. Человек неподвижен относительно Земли и рассматривает Землю как систему отсчета, в то время как самолет и автомобиль в данном случае являются движущимися телами. Но пассажир в машине, который говорит, что дорога уходит из-под колес, тоже прав. Он считает, что автомобиль — это система отсчета (он неподвижен относительно автомобиля), а Земля в данном случае — движущееся тело.

Чтобы определить изменение положения тела в пространстве, необходимо установить следующее соотношение. систему Координаты. Система координат — это метод определения положения объекта в пространстве.

В физике наиболее распространенным является декартов прямоугольник. система Система координат с тремя перпендикулярными линейными осями — абсцисса ( ), ордината ( ) и аппликата ( ). Единицей измерения длины в СИ является метр.

Ориентация в поле основана на полярности системой Координаты. С помощью карты определите расстояние до нужного населенного пункта. Направление движения определяется азимутом, то есть углом, который образует нулевое направление с линией, соединяющей человека с желаемым местом. Таким образом, в полярном системе координаты — это расстояние и угол.

В географии, астрономии и при расчете движения спутников и космических кораблей положение всех тел задается в сферической форме системе координаты. Для определения положения точки в пространстве в сферических координатах системе Даны координаты, расстояние от начала координат и углы, образующие радиус-вектор с плоскостью Гринвичского меридиана (долгота) и экваториальной плоскостью (широта).

Что такое движение материальной точки

В механике рассматривают перемещение объектов. Принципы характерны для материальной точки и твердого тела. Термин «материальная точка» введен с целью упростить решение практических задач. В случае, когда габариты объекта существенно меньше, чем расстояние, которое он преодолевает, либо размеры других тел, то условно данный объект обозначают материальной точкой.

Определение

Кинематика — раздел механики, изучающий математическое описание движения идеализированных тел, без рассмотрения причин движения.

Определение

Движением материальной точки в пространстве называют изменение ее положения по отношению к другим телам с течением времени.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Пример

Для расчета физических характеристик самолета относительно Земли в полете можно представить его в виде материальной точки. Однако если рассматривается система, которая включает самолет и пассажира, летящего в нем, то в данном случае принимать транспортное средство за материальную точку нецелесообразно. Таким образом, движение материальной точки рассматривают только в том случае, когда размерами объекта в конкретной ситуации можно пренебречь.

В одинаковое время положение точки в пространстве может отличаться в зависимости от того, относительно какого тела осуществляются наблюдения. С помощью системы координат и тела отсчета описывают перемещение материальной точки в пространстве. Согласно элементарным математическим закономерностям, задать положение какой-либо точки на плоскости можно, воспользовавшись системой координат.

Определение

Прямые, которые взаимно перпендикулярны и пересекаются в одной точке, являются координатными прямыми. А данная точка пересечения носит название начала координат.

Из начала координат можно вывести еще одну прямую, которая будет являться перпендикуляром к плоскости. Подобная система позволит задать положение точки в пространстве. Другим методом является применение радиус-вектора.

Определение

Радиус-вектор представляет собой отрезок, который провели из точки начала координат к заданной точке.

В течение времени движущаяся материальная точка меняет свое положение в пространстве. Для того чтобы выполнить расчет положения точки в какой-либо определенный момент времени, необходимо провести измерения времени.

Определение

Совокупность тела отсчета, связанной с ним системы координат и прибора отсчета времени представляет собой систему отсчета.

Выбор системы отсчета определяется следующими характеристиками:

• траектория;
• пройденный путь;
• перемещение;
• скорость.

Пример

Можно рассмотреть движение двух автомобилей, которые находятся на соседних полосах и перемещаются в одном направлении с равными скоростями. Когда телом отсчета является одно из этих транспортных средств, при заданной системе отсчета скорость, путь и перемещение второго транспорта будут иметь нулевые значения. Таким образом, второй автомобиль по сравнению с первым находится в состоянии покоя. В случае, когда в качестве тела отсчета выбрана дорога, значения скорости, пути и перемещения будут отличны от нуля.

Определение

Траектория материальной точки — линия, которую очерчивает материальная точка, двигаясь в пространстве.

Траектория включает множество точек, в которых рассматриваемая материальная точка была зафиксирована в прошедший момент времени, находится в данное время и будет замечена в будущий временной период.

Определение

Перемещением материальной точки называют вектор, берущий начало в точке траектории в начальный промежуток времени и заканчивающийся в точке траектории в конечный момент времени.

Определение

Путь материальной точки представляет собой сумму всех отрезков, пройденных материальной точкой в процессе движения.

Путем называют скалярную величину, которая всегда характеризуется положительным значением. При перемещении материальной точки пройденный ей путь может только увеличиваться.

Определение

Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.

Виды систем отсчета и их применение

Система отсчета – это набор правил и конвенций, которые определяют способ измерения и записи числовых значений. В зависимости от конкретной задачи и требований, можно выбрать различные виды систем отсчета.

Ниже представлены некоторые из популярных видов систем отсчета и их применение:

Десятичная система отсчета

• Наиболее распространенная система отсчета, использующая 10 цифр (от 0 до 9).
• Применяется в повседневной жизни, научных расчетах, финансовой отчетности и других сферах.
• Позволяет легко выполнять математические операции, такие как сложение, вычитание, умножение и деление.

Двоичная система отсчета

• Использует всего две цифры – 0 и 1.
• Широко применяется в компьютерах и другой цифровой технике, где информация хранится и обрабатывается в виде двоичных чисел.
• Основана на принципе работы электронных переключателей, которые могут находиться в двух состояниях – включено или выключено.

Шестнадцатеричная система отсчета

• Использует 16 цифр – от 0 до 9 и от A до F.
• Часто применяется в программировании и информатике при работе с памятью компьютера, адресами и шифрованием данных.
• Обеспечивает более компактное представление больших чисел по сравнению с десятичной системой.

Другие системы отсчета

• Существует множество других систем отсчета, таких как восьмеричная, двадцатиричная, позиционные системы отсчета и т.д.
• Каждая система имеет свои особенности и может применяться в определенных областях, таких как контрольные суммы, сетевые адреса, системы счисления времени и другие.

Выбор подходящей системы отсчета зависит от ожидаемого результата и условий конкретной задачи. Понимание различных систем отсчета позволяет более эффективно работать с числовыми данными и выполнять различные вычисления.

Упражнения

Упражнение №1

Можно ли считать автомобиль материальной точкой в следующих уловиях:а) при определении пути, который он прошел за $2 \space ч$, двигаясь со средней скоростью, равной $80 \frac{км}{ч}$;б) при обгоне им другого автомобиля?

Посмотреть ответ

Скрыть

Ответ:

В первом случае за указанное время автомобиль пройдет путь:$s = \upsilon_{ср} t$,$s = 80 \frac{км}{ч} \cdot 2 \space ч = 160 \space км$.

Очевидно, что такое расстояние намного больше размеров самого автомобиля. Поэтому в данном случае мы можем рассматривать его как материальную точку.

Во втором случае (когда автомобиль идет на обгон) мы не можем считать его материальной точкой. Ведь в этом случае для нас будут важны габариты автомобиля и движение отдельных его точек.

Упражнение №2

Самолет совершает перелет из Москвы во Владивосток. Может ли рассматривать самолет как материальную точку диспетчер, наблюдающий за его движением; пассажир этого самолета?

Посмотреть ответ

Скрыть

Ответ:

Диспетчер, являющийся телом отсчета, может рассматривать самолет как материальную точку, потому что размеры самолета намного меньше пролетаемого им расстояния.

А вот пассажир самолета не может принимать его за материальную точку, ведь он движется вместе с ним.

Упражнение №3

Когда говорят о скорости машины, поезда и других транспортных средств, тело отсчета обычно не указывают. Что подразумевают в этом случае под телом отсчета?

Посмотреть ответ

Скрыть

Ответ:

В случаях, когда речь идет о скоростях транспортных средств, под телом отсчета обычно подразумевают земную поверхность или любое тело, находящееся в состоянии покоя относительно Земли.

Упражнение №4

Мальчик стоял на земле и наблюдал, как его младшая сестра каталась на карусели. После катания девочка сказала брату, что и он сам, и дома, и деревья быстро проносились мимо нее. Мальчик же стал утверждать, что он вместе с домами и деревьями был неподвижен, а двигалась сестра. Относительно каких тел отсчета рассматривали движение девочка и мальчик? Объясните, кто прав в споре.

Посмотреть ответ

Скрыть

Ответ:

Наблюдающий за каруселью мальчик рассматривал движение карусели относительно поверхности Земли. Так, ни деревья, ни дома, ни сам мальчик не двигались относительно друг друга. Двигались только карусель и девочка на ней.

Девочка же рассматривала движение относительно своего сиденья карусели. Поэтому для нее в движении находились все остальные окружающие предметы (деревья, дома и др.)

Получается, что в этом споре правы оба. Просто брат с сестрой рассматривали движение относительно разных тел отсчета.

Упражнение №5

Относительно какого тела отсчета рассматривают движение, когда говорят: 

• скорость ветра равна $5 \frac{м}{с}$;
• бревно плывет по течению реки, поэтому его скорость равна нулю;
• скорость плывущего по реке дерева равна скорости течения воды в реке;
• любая точка колеса движущегося велосипеда описывает окружность;
• Солнце утром восходит на востоке, в течение дня движется по небу, а вечером заходит на западе?

Посмотреть ответ

Скрыть

Ответ:

• скорость ветра оценивают относительно поверхности Земли;
• плывущее бревно рассматривают относительно поверхности реки, которая сама находится в движении;
• дерево плывет со скоростью течения воды в реке, если рассматривать его движение относительно берега;
• точки колеса велосипеда движутся по окружности относительно самого велосипеда;
• движение Солнца по небу рассматривается относительно линии горизонта.

Роль системы отсчета в различных сферах

Система отсчета является неотъемлемой частью различных сфер деятельности. Она позволяет нам совершать измерения, устанавливать порядок и организовывать данные. Вот несколько примеров, как система отсчета играет важную роль в различных сферах:

1. Наука

В науке система отсчета используется для измерения физических величин, таких как длина, масса, время и температура. Она позволяет исследователям получать точные и повторяемые результаты, которые могут быть проанализированы и сравнены. Например, в физике система отсчета позволяет нам измерять скорость движения объектов, а в химии — точно определять концентрацию веществ в растворах.

2. Техническое обслуживание

В техническом обслуживании система отсчета играет важную роль в процессе ремонта и обслуживания технических устройств. Она позволяет инженерам и техникам определить точные параметры и измерения, необходимые для настройки и наладки устройств. Благодаря системе отсчета технические специалисты могут работать с высокой точностью и эффективностью.

3. Финансы и бухгалтерия

В финансовой сфере система отсчета используется для учета доходов, расходов и активов компаний. Она позволяет финансовым аналитикам и бухгалтерам следить за финансовым состоянием организации, делать анализы и прогнозы. Система отсчета в финансах обеспечивает единый стандарт измерения, что позволяет сравнивать данные между различными компаниями и сезонами.

4. Информационные технологии

В информационных технологиях система отсчета играет роль в организации данных и определении порядка их хранения. Например, в базах данных система отсчета используется для уникальной идентификации записей и установки их последовательности. Она также применяется в алгоритмах и программировании для установления порядка выполнения операций.

5. Спорт

В спорте система отсчета применяется для отслеживания времени, количества очков, дистанции и других показателей. Она позволяет судьям и тренерам оценивать результаты и выставлять очки, а также устанавливать рекорды и подводить итоги соревнований. Система отсчета в спорте обеспечивает объективность и справедливость в результатах, а также способствует мотивации спортсменов к достижению лучших результатов.

Таким образом, система отсчета играет важную роль в различных сферах деятельности, обеспечивая точные измерения, порядок и организацию данных. Без нее было бы сложно проводить измерения, анализировать результаты и принимать обоснованные решения.

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета

То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение

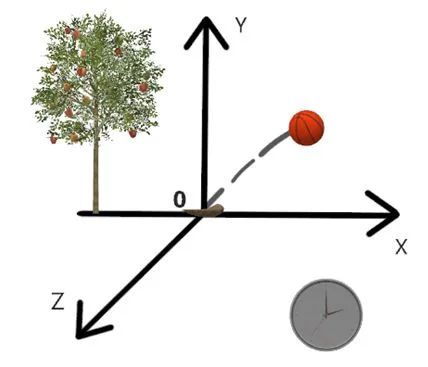Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку. Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как  материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Система отсчёта в физике — что это, определение и виды

С точки зрения современной физики, всякое движение можно признать относительным. Таким образом, любое движение тела можно рассматривать исключительно по отношению к другому материальному объекту или же совокупности таких объектов. Например, мы не можем указать, каков характер движения Луны в общем, но может определить её перемещение относительно Солнца, Земли, Звёзд, других планет и пр.

В ряде случаев подобная закономерность бывает связана не с единой материальной точкой, а с множеством базовых точек отсчёта. Эти базовые тела отсчёта могут задавать совокупность координат.

Примеры решения задач по теме «Относительность движения»

Задание	Аэроплан движется относительно воздуха со скоростью 50 м/с. Скорость ветра относительно земли составляет 15 м/с. Какова скорость самолета относительно земли, когда он движется по ветру или против ветра? перпендикулярно направлению ветра?
Решение	В этом случае скорость — это скорость самолета относительно земли (постоянная системы Reference), относительная скорость самолета — это скорость самолета относительно воздуха (moving). системы Ссылка), скорость движущегося системы отсчета относительно неподвижной — это скорость ветра относительно земли.

Повернем ось в направлении ветра.

Запишем закон сложения скоростей в векторной форме:

Спроектированное на ось, это уравнение переписывается следующим образом:

Подставив числовые значения в формулу, мы можем рассчитать скорость самолета относительно земли:

(м/с)

Запишем закон сложения скоростей в векторной форме:

Спроектированное на ось, это уравнение переписывается следующим образом:

Подставив числовые значения в формулу, мы можем рассчитать скорость самолета относительно земли:

(м/с)

В этом случае мы используем системой координат, с координатными осями, как показано на рисунке.

Мы складываем векторы и по правилу сложения векторов. Скорость самолета относительно земли:

(м/с)

Это значение является мерой вектора скорости. Чтобы определить направление скорости самолета, нам нужно вычислить:

Итак, относительно земли самолет движется со скоростью 52,2 м/с под углом к горизонтальному направлению OX.

«Механическое движение. Траектория и путь»

Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Изучение механики традиционно начинают с кинематики.

Кинематика — раздел механики, в котором рассматривают способы описания механического движения тел без выяснения причин изменения характера их движения. Сами причины рассматриваются в других разделах механики.

Траектория движения — это линия, вдоль которой движется тело.

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец — с конечным положением точки. Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь — это длина траектории, пройденной телом. Путь — всё расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения. Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и модуля перемещения тела, и модуля изменения координаты тела.

Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).

Виды траекторий. Если тело движется вдоль прямой, движение называют прямолинейным. Траектория в этом случае — отрезок прямой. Если же траектория — кривая линия, движение называют криволинейным.

Относительность движения

Для того чтобы описать положение данного тела в пространстве, необходимо:

1. выбрать тело отсчёта и начало отсчёта на нём;
2. связать с ним координатную ось, проходящую через начало отсчёта в нужном направлении, и указать единицу длины.

При этом расстояние от начала отсчёта до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.

https://youtube.com/watch?v=Vz3tdk7zT1s

Система отсчета

Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчёта. Если мы выберем в качестве тела отсчёта другое тело или другую ось координат, то и координата данного тела может стать другой. Совокупность тела отсчёта, с которым связана ось координат, и часов называют системой отсчёта.

Если координата тела не изменяется с течением времени в выбранной системе отсчёта, то говорят, что это тело в данной системе отсчёта неподвижно, или покоится.

Если координата тела выбранной системы отсчёта увеличивается со временем, то говорят, что тело движется в положительном направлении координатной оси. Напротив, если координата тела в выбранной системе отсчёта со временем уменьшается, то говорят, что тело движется в отрицательном направлении координатной оси.

Нельзя сказать, как движется тело, если не сказать, в какой системе отсчёта рассматривается это тело. Иначе говоря, одно и то же тело в разных системах отсчёта может двигаться по-разному (в том числе и покоиться).

Конспект по физике в 7 классе по теме «Механическое движение. Траектория».

Следующая тема: Прямолинейное равномерное движение

Пространственная система отсчета

Разберем предложенный выше алгоритм, вернее его первый пункт. Как определить положение тела в первоначальный момент? Вы сможете это сделать только добавив к системе еще одно тело.

Для того, чтобы понять для чего, попробуйте объяснить кому-нибудь, где лежит ваш мобильный телефон, не назвав при этом ни одного другого предмета. В случае удачи, милости прошу в комментарии. Скорее всего у вас ничего не вышло. Для того, чтобы определить положение предмета, вы обычно ссылаетесь на другой предмет, используя его в качестве системы отсчета.

Дело в том, что понятие абсолютного положения тела бессмысленно. Для того чтобы это словосочетание имело смысл, должно существовать некое “абсолютной пространство”, относительно которого вы могли бы рассматривать это тело. Но его не существует.

Поэтому под положением тела, мы всегда будем понимать относительное положение. Т.е. положение тела всегда будет рассматриваться относительно другого тела или системы тел, называемых пространственной системой отсчета. Дадим определение используя все тот же учебник физики уважаемого Д.В.Сивухина:

От выбора пространственной системы отсчета зависит сможете ли вы зарегистрировать факт движения или нет. Для ясности вам необходимо рассмотреть предложенный пример.

Неинерциальные системы отсчёта

С планетой Земля связывают и инерциальные, и неинерциальные системы отсчёта. При этом нужно понимать, что допущение о том, что Земля – инерционная система, по космическим масштабам очень грубое. Тем не менее, этого грубого приближения достаточно для описания многих процессов, проходящих на поверхности планеты. В частности, движение сухопутного транспорта, движение шаров на биллиардном столе и т. д. точно описывается в этом приближении.

Земля движется вокруг собственной оси. Это движение необходимо учитывать, например, при запуске космических аппаратов. В системе отсчёта, связанной с Землёй, ракета, стартовавшая вертикально, совершает также видимое движение в горизонтальном направлении. Это логично: место старта ракеты смещается вместе со всей поверхностью планеты из-за её вращения. Подобные отклонения траектории, свойственные неинерциальным системам, чисто математически описывают с помощью инерциальных сил (сил, которых на самом деле не существует, но принятие которых в расчёт помогает чисто формально отнести систему отсчёта к числу инерциальных). В данном случае математически видимое отклонение ракеты от прямой траектории описывается силой Кориолиса, которая якобы действует на неё.

Сферическая система координат

В декартовой системе координат положение точки в пространстве описывается с помощью упорядоченной тройки осей, в которой каждая координата представляет собой расстояние. В цилиндрической системе координат положение точки в пространстве описывается двумя расстояниями (r и z ) и угла (θ). В сферической системе координат мы снова используем упорядоченную тройку осей для описания положения точки в пространстве. В данном случае оси описывают одно расстояние и два угла. Сферические координаты упрощают описание сферы, так же как цилиндрические координаты упрощают описание цилиндра. Линии сетки для сферических координат основаны на измерениях углов, как и для полярных координат.

Теорема

В сферической системе координат точка P в пространстве (рис. 4) представлена упорядоченной тройкой \

Где:

\ — это расстояние между P и началом координат \;

\ — тот же угол, который используется для описания местоположения в цилиндрических координатах;

\ — это угол, образованный положительной осью z и отрезком прямой OP, где О это начало координат и \

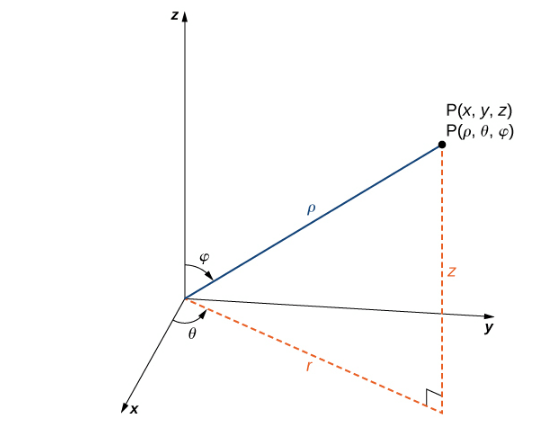Рис. 4 Связь между сферическими, декартовыми и цилиндрическими координатами.

Условно начало координат представлено как (0,0,0) в сферических координатах.

Преобразование между сферическими, цилиндрическими и прямоугольными координатами

Декартовые координаты \ и сферические координаты \ связаны следующим образом:

\

\ — уравнения для преобразования из сферических координат в   квадратные (декартовы).

\ и \

\ — уравнения для преобразования из декартовых в сферические.

\

Если точка имеет цилиндрические координаты \, тогда эти уравнения определяют связь между цилиндрическими и сферическими координатами.

\

\ — уравнения для преобразования из сферических координат в цилиндрические.

\ и \

\  — уравнения для преобразования из цилиндрических в сферические.

\

Формулы для преобразования сферических координат в прямоугольные могут показаться сложными, но это простые приложения тригонометрии. Глядя на рисунок 5, легко увидеть, что \. Затем, глядя на треугольник на плоскости xy с \ в качестве его гипотенузы имеем \.  Вывод формулы для y похож. Рисунок 3 также показывает, что \ и  \.  Решая это последнее уравнение для  \  а затем подставив  \ (из первого уравнения) дает  \

Также обратите внимание, что, как и прежде, мы должны быть осторожны при использовании формулы \ выбрать правильное значение \

Существуют и другие криволинейные системы координат, с помощью которых можно найти координаты заданной точки: параболические, гиперболические, эллиптические и другие. Система отсчета подбирается для каждого случая индивидуально с учетом особенности движения тела, с помощью которой определяется простейший закон движения того или иного тела или точки.

Временные промежутки, расстояния, и их однородность

Специальная теория относительности связывает временные промежутки и пространство. В Материальной вселенной существует 3 известных измерения в пространстве: вправо и влево, вперед и назад, вверх и вниз. Если добавить к ним другое измерение, названное временным, то это составит основу пространственно-временного континуума.

Если Вы осуществляете движение с малой скоростью, ваши наблюдения не будут сходиться с людьми, которые двигаются быстрее.

Позже эксперименты подтвердили, что пространство, так же как и время, не может восприниматься одинаково: от скорости движения объектов зависит наше восприятие.

Абсолютная система отсчёта

В физике конкретная СЦ часто считается наиболее удобной (привилегированной) для решения конкретной задачи — определяется простотой вычислений или записи уравнений динамики тела и полей внутри него. Обычно такая Эта возможность связана с симметрией проблемы.

С другой стороны, раньше считалось, что существует «фундаментальная» система отсчёта, простота записи законов природы, которая отличала его от всех других. систем. Физики 19 века, например, считали, что система, Основанная на эфире электродинамика Максвелла была привилегированной и поэтому называлась абсолютной системой отсчета (ARS). В современном мышлении не существует системы отсчёта, выделенной именно таким такой системы отсчета не существует, так поскольку законы природы, выраженные в тензорной форме, имеют одинаковую форму во всех странах системах отсчёта — т.е. во всех точках пространства и во всех точках времени. Это условие — локальная инвариантность пространства-времени — является одной из проверяемых основ физики.

Виды систем отсчёта

Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.

Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.

Инерциальные системы отсчёта

Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.

1. Существование таких совокупностей подчиняется первому закону Ньютона.
2. Именно в таких сетках возможно наиболее простое описание движения тел.
3. По существу, инерциальная структура — это всего лишь идеальна математическая модель. Найти такую структуру в физическом мире не представляется возможным.

Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.

Неинерциальные системы отсчёта

Неинерциальные разновидности наравне с инерциальными связываются с планетой Земля. Учитывая космические масштабы, считать Землю инерциальной совокупностью можно весьма грубо и приблизительно.

Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.

Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.

Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.