Физика

Линзы. Оптическая сила линзы

Линза – это прозрачное тело, ограниченное двумя сферическими или криволинейными поверхностями, одна из которых может быть плоской.

Тонкая линза – физическая модель линзы, в которой ее толщиной можно пренебречь по сравнению с диаметром линзы.

Классификация линз

1. По форме:

• выпуклые – это линзы, у которых средняя часть толще, чем края;
• вогнутые – это линзы, у которых края толще, чем средняя часть.

2. По оптическим свойствам:

собирающие – это линзы, после прохождения которых параллельный пучок лучей собирается в одной точке;

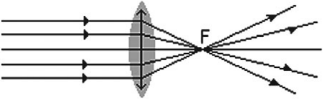
рассеивающие – это линзы, после прохождения которых параллельный пучок лучей рассеивается.

Условные обозначения:

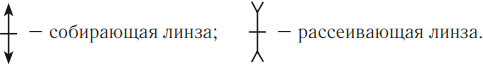
Величины, характеризующие линзу

Главная оптическая ось – это прямая, проходящая через центры сферических поверхностей линзы.

Оптический центр линзы – это точка пересечения главной оптической оси с линзой, проходя через которую луч не изменяет своего направления.

Побочная оптическая ось – это любая прямая, проходящая через оптический центр линзы под произвольным углом к главной оптической оси.

Фокус линзы – это точка, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси.

Обозначение – ​\( F \)​.

Фокусное расстояние – это расстояние от оптического центра линзы до ее фокуса. Обозначение – \( F \), единица измерения – м.

Фокальная плоскость – это плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.

Побочный фокус – это точка пересечения побочной оптической оси с фокальной плоскостью.

Оптическая сила линзы – это величина, обратная фокусному расстоянию.

Обозначение – ​\( D \)​, единица измерения – диоптрия (дптр):

1 дптр – это оптическая сила линзы с фокусным расстоянием 1 м.

Важно!
Оптическая сила линзы зависит от показателя преломления линзы и от радиусов кривизны сферических поверхностей, ограничивающих линзу:

где ​\( n_л \)​ – показатель преломления линзы, ​\( n_{ср} \)​ – показатель преломления среды, ​\( R_1 \)​ и \( R_2 \) – радиусы сферических поверхностей.

Если поверхности выпуклые, то ​\( R_1 \)​ > 0 и \( R_2 \) > 0, если поверхности вогнутые, то \( R_1 \) < 0 и \( R_2 \) < 0.

Если одна из поверхностей линзы плоская, например первая, то ​\( R_1\to\infty \)​, а вторая поверхность выпуклая: \( R_2 \) > 0, то

Примеры действительных изображений

В физике существует два типа изображений: действительное и мнимое. Отличие между ними заключается в том, каким образом свет распространяется от объекта до наблюдателя.

Действительное изображение образуется, когда свет проходит через оптическую систему и сходится в точку на фокусном расстоянии. При этом изображение можно увидеть на экране или пленке. Вот несколько примеров действительных изображений:

1. Изображение на экране телевизора: Когда мы смотрим телевизионное шоу или фильм, свет отображается на экране и создает действительное изображение, которое мы видим.

2. Изображение на фотографии: Когда фотографируем предмет или сцену, свет попадает на пленку или сенсор камеры и создает действительное изображение.

3. Изображение в зеркале: Когда мы смотрим в зеркало, свет отражается от поверхности зеркала и формирует действительное изображение нашего отраженного образа.

Таким образом, действительные изображения возникают, когда свет фокусируется и формирует точное отражение предмета на экране или другой поверхности.

Формирование изображения в объективе камеры

Изображение в объективе камеры формируется за счет оптических свойств объектива и процессов преломления и отражения света. В результате, на плоскости фокусировки формируется действительное изображение объекта.

Отличие между действительным и мнимым изображениями заключается в том, что действительное изображение может быть фокусировано на плоскости фокусировки и рассмотрено невооруженным глазом или захвачено камерой. Такое изображение передает истинные размеры, форму и положение объекта.

С другой стороны, мнимое изображение формируется в ситуациях, когда отраженные или преломленные лучи не сходятся в одной точке и не могут быть зафиксированы на плоскости фокусировки. Когда мы видим мнимое изображение, мы, по сути, наблюдаем фиктивные лучи света, которые не существуют в реальности.

На практике, чтобы определить, является ли изображение действительным или мнимым, можно использовать специальные оптические инструменты, такие как линзы или зеркала. Эти инструменты могут изменять направление лучей света и фокусировать их на плоскости.

Надеемся, что эта информация помогла вам разобраться в отличии между действительным и мнимым изображениями. Если у вас возникнут еще вопросы, пожалуйста, обращайтесь за помощью.

Отражение света от объекта наших глаз

В физике отражение света играет важную роль при рассмотрении образов, которые мы видим. При взаимодействии света с объектом происходит его отражение, и эти отраженные лучи попадают в наши глаза, создавая изображение.

Изображение, которое мы видим, может быть двух типов: действительным и мнимым. Различие между этими типами изображений заключается в том, где находится источник света, отражающегося от объекта.

Действительное изображение возникает, когда отраженные лучи света сходятся в реальной точке пространства. Это означает, что источник света находится за объектом и лучи света от него сталкиваются в точке, создавая фокусированное изображение на поверхности, на которую они попадают.

С другой стороны, мнимое изображение возникает, когда отраженные лучи света не сходятся в реальной точке пространства. Это означает, что источник света находится между объектом и поверхностью отражения. Лучи света от источника отходят в разные стороны и видимость объекта в наших глазах создается только благодаря эффекту отражения от поверхности.

Примером действительного изображения может служить отражение объекта в зеркале, где источник света (например, лампа) находится за зеркалом и лучи света сходятся, создавая четкое изображение. Примером мнимого изображения может служить отражение объекта в плоскости воды, где источник света (например, солнце) находится между наблюдателем и поверхностью воды, и отраженные лучи расходятся в разные стороны, создавая миррорное отражение, но не формируя действительного изображения.

Отличие между действительным и мнимым изображениями важно понимать в физике, поскольку оно объясняет, как свет взаимодействует с объектами и как мы видим окружающий нас мир. Если у вас возникли вопросы по данной теме, пожалуйста, обратитесь за помощью к преподавателю или другому специалисту

Линзы. Какими они бывают?

Управлять световыми пучками можно еще с помощью одного изобретения. Это очки – не только помогающие хорошо видеть, вставленные в оправу линзы, а устройства, управляющие светом.

Схематически с использованием геометрических построений линзу можно представить так:

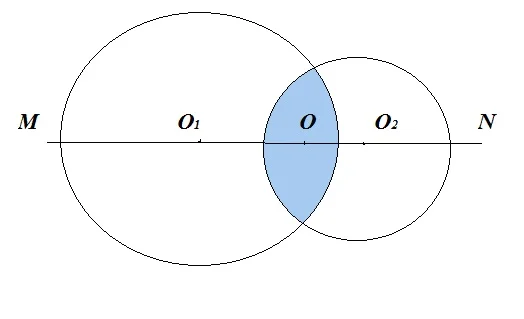
У элементов линзы есть специальные названия:

Тут на картинке

Если с точки зрения геометрии сферические поверхности пересекаются, такая линза называется выпуклой. Края ее много тоньше середины.

По-другому образуется вогнутая линза. Геометрические поверхности ее не пересекаются, а отдалены на некоторое расстояние.

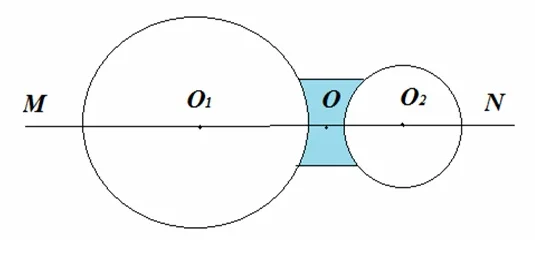
Сочетание закругленных поверхностей определяет свойства различных линз. Они по-разному изменяют направления лучей.

Световые лучи дважды преломляются, проходя линзу. Первый раз на входе в линзу, второй раз при выходе из нее. Дальше лучи или пересекаются, или расходятся в разные стороны.

Прохождение лучей сквозь линзы.

У всех линз есть важнейшая характеристика.

Выпуклая линза собирает лучи в одну точку, называемую фокусом линзы (F).

Из вогнутой линзы лучи выходят расходящимся пучком. Но и здесь есть фокус, только мнимый. Он находится перед линзой в точке, где пересекаются продолжения расходящихся лучей. Название «мнимый» фокус получил, потому что пересекаются не сами лучи, а прямые, на которых они располагаются.

Линзы бывают различными. Их свойства зависят от вида образующих поверхностей.

Собирающие:

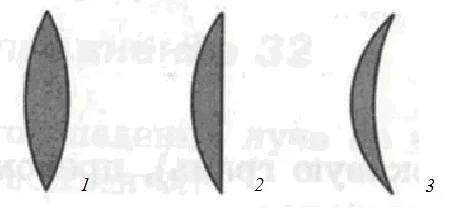
      1 – двояко-выпуклая;

      2 – плоско-выпуклая;

       3 – вогнуто-выпуклая.

Рассеивающие:

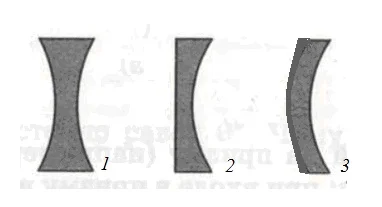
1 – двояко-вогнутая;

   2 – плоско-вогнутая;

   3 – выпукло-вогнутая.

Основной особенностью собирающих линз является то, что расстояние между поверхностями в центре больше, чем по краям. У рассеивающих линз, наоборот, в центре расстояние между поверхностями меньше, чем по краям.

Главное отличие линз.  

Такое строение и определяет ход лучей на выходе из линз (лучи пересекаются или расходятся).

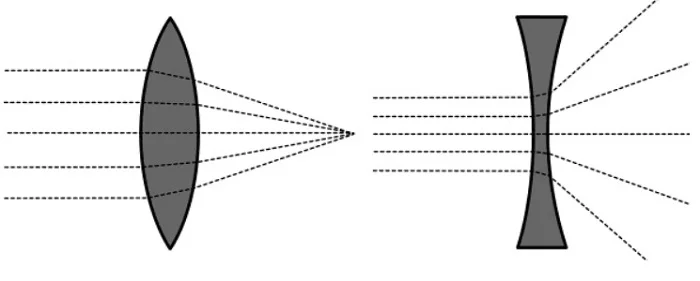Ход лучей в линзах разного типа.

Линза

• Линза будет собирающей, если луч, преломляясь, отклоняется от первоначального направления к главной оптической оси, и рассеивающей, если луч отклоняется от оси.
• для получения изображения необходимо не менее двух лучей.

При решении задач с системой линз задача разбивается на несколько частей (по числу линз):

1 часть – рассматривается только первая к предмету линза (все остальные линзы не рассматриваются и никак не влияют на решение);

2 часть – рассматривается только вторая линза, а предметом для нее служит изображение от первой линзы и т.д.

Построение в линзах

При построении изображения точек выбирают любые два из трех стандартных лучей.

Для собирающей линзы (рис. 2)

1. луч, параллельный главной оптической оси, после преломления проходит через главный фокус;
2. луч, совпадающий с побочной оптической осью, проходит без преломления через центр линзы;
3. луч, проходящий через главный фокус перед линзой, после преломления идет параллельно главной оптической оси.

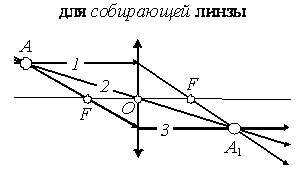
Рис. 2

Для рассеивающей линзы (рис. 3)

1. луч, параллельный главной оптической оси, после преломления направлен так, что его продолжение проходит через главный фокус перед линзой;
2. луч, совпадающий с побочной оптической осью, проходит без преломления через центр линзы;
3. луч, направленный на главный фокус за линзой, после преломления идет параллельно главной оптической оси.

Рис. 3

Для построения изображения отрезка АВ необходимо построить изображения А1 и В1. Полученный отрезок А1В1 и будет изображением отрезка АВ.

Виды изображения

Виды изображения:

1) действительное или мнимое;

2) прямое или перевернутое;

3) увеличенное или уменьшенное.

Некоторые свойства изображений:

• если предмет перпендикулярен главной оптической оси, то его изображение также будет перпендикулярным этой оси;
• если точка лежит на главной оптической оси, то ее изображение также будет лежать на этой оси;
• мнимое изображение получается в рассеивающих линзах во всех случаях, и в собирающей линзе, если расстояние от предмета до линзы меньше фокусного.

Дополнительные лучи при построении

При построении можно воспользоваться следующим свойством:

все лучи света, направленные параллельно побочной оптической оси, после преломления собираются в побочном фокусе (рис. 4).

• Все побочные фокусы лежат на фокальной плоскости, проходящей перпендикулярно главной оптической оси.
• В собирающей линзе пересекаются в фокальной плоскости преломленные лучи (поэтому рассматривают фокальную плоскость, лежащую за линзой).
• В рассеивающей линзе пересекаются в фокальной плоскости продолжения преломленных лучей (фокальная плоскость, лежащей перед линзой).

Рис. 4

Оптическая сила линзы

\(~D = \frac{1}{F}\) ,

где F – фокус линзы (м); D – оптическая сила линзы (дптр)

ОБРАТИТЕ ВНИМАНИЕ, что в некоторой физической литературе учитывают знаки в величинах, тогда:

• если линза собирающая, то F > 0, D > 0;
• если линза рассеивающая, то F < 0, D < 0.

В данном пособии знаки будем учитывать в формулах при помощи правила знаков. Тогда в условиях будем учитывать только значения величин.

\(~D_0 = \pm D_1 \pm D_2 \pm \ldots \pm D_N\) ,

где D – оптическая сила системы вплотную сложенных N тонких линз (дптр); D₁, D₂, …, D_N – оптические силы тонких линз системы (дптр).

Правило знаков:

• знак «+» ставится, если линза собирающая;
• знак «–» – линза рассеивающая.

Формула тонкой линзы

\(~\pm \frac{1}{F} = \pm \frac{1}{d} \pm \frac{1}{f}\) ,где

Правило знаков:

F – фокусное расстояние линзы (м).

• знак «+» ставится, если линза собирающая;
• знак «–» – линза рассеивающая;

d – расстояние от предмета до линзы (м),

• знак «+» ставится, если предмет действительный (лучи, падающие на линзу, расходящиеся);
• знак «–» – предмет мнимый (лучи сходящиеся);

f – расстояние от изображения до линзы (м),

• знак «+» ставится, если изображение действительное;
• знак «–» – изображение мнимое (изображение получатся пересечением продолжения лучей).

Пусть на оптическую систему падает расходящийся пучок лучей, пересекающихся в точке S (рис. 5 а, оптическая система изображена прямоугольником). В этом случае S – это действительный источник (предмет).

Если на оптическую систему падает сходящийся пучок лучей и продолжения этих лучей пересекаются в точке S (рис. 5 б), то S – это мнимый источник (предмет).

Рис. 5

Увеличение линзы

\(~\Gamma = \frac{H}{h}\) ,

где Г – увеличение линзы; H – высота изображения (м); h – высота предмета (м).

\(~\Gamma = \frac{f}{d}\) ,

где Г – увеличение линзы; f – расстояние от изображения до линзы (м); d – расстояние от предмета до линзы (м).

Статическая и динамическая рефракция глаза

Рефракция – это оптическая установка глазного яблока при фокусировке на удаленных предметах.

Если глаз нормальный, то пучок параллельных лучей, идущих от бесконечно далекого предмета, преломляются таким образом, что фокус их совпадает с центральной ямкой сетчатки. Такое глазное яблоко называется эмметропическим. Однако, далеко не всегда человек может похвастаться такими глазами.Например, близорукость сопровождается увеличением длины глазного яблока (превышает 22,5-23 мм) или увеличением преломляющей силы глаза за счет изменения кривизны хрусталика. При этом параллельный пучок света не попадает на зону макулы, а проецируется перед ней. В результате на плоскость сетчатки попадают уже расходящиеся лучи. В этом случае изображение получается расплывчатым. Глаз называют миопическим. Чтобы изображение стало четким, необходимо передвинуть фокус на плоскость сетчатки. Этого можно достичь в том случае, если пучок света имеет не параллельные, а расходящиеся лучи. Этим можно объяснить тот факт, что близорукий пациент хорошо видит вблизи.

Для контактной коррекции миопии применяют двояковогнутые линзы, способные отодвинуть фокус в зону макулы. Этим можно компенсировать повышенную преломляющую способность вещества хрусталика. Довольно часто миопия носит наследственный характер. При этом пик заболеваемости приходится на школьный возраст и связан с нарушением гигиенических правил. В тяжелых случаях миопия способна вызвать вторичные изменения сетчатки, которые могут сопровождаться значительным снижением зрения и даже слепотой

В связи с этим очень важно вовремя проводить профилактические и лечебные мероприятия, в том числе правильно питаться, заниматься физкультурой, соблюдать гигиенические рекомендации

Дальнозоркость сопровождается уменьшением длины глаза или снижением коэффициента преломления оптических сред. При этом пучок параллельных лучей от далекого предмета попадает за плоскость сетчатки. В макуле же проецируется участок сходящихся лучей, то есть изображение получается размытым. Глаз называют при этом дальнозорким, то есть гиперметропическим. В отличие от нормального глаза, ближайшая точка ясного видения в этом случае отстоит на некоторое расстояние. Для коррекции гиперметропии можно использовать двояко выпуклые линзы, способные увеличить преломляющую силу глаза

Важно понимать, что истинная врожденная или приобретенная дальнозоркость отличается от пресбиопии (старческой дальнозоркости)

При астигматизме нарушена способность концентрировать лучи света в одной точке, то ест фокус представлен пятном. Связано это с тем, что кривизна хрусталика различается по разным меридианам. При большей преломляющей способности по вертикали, астигматизм принято называть прямым, при увеличении горизонтальной составляющей – обратным. Даже в случае нормального глазного яблока оно несколько астигматично, так как идеально ровной роговицы не бывает. Если рассматривать диск с концентрическими кругами, то возникает незначительное их сплющивание. Если астигматизм приводит к нарушению зрительной функции, то его корректируют с использованием цилиндрических линз, которые располагают в соответствующих меридианах.

4.6.6 Рассеивающая линза: мнимое изображение точки

К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.

Снова берём луч SO и произвольный луч SX (рис. 4.50
). На выходе из линзы имеем два расходящихся луча OE и XY , которые наш глаз достраивает до пересечения в точке S0
.

	F A0

Рис. 4.50. Мнимое изображение точки S в рассеивающей линзе

Нам снова предстоит доказать теорему об изображении о том, что точка S0
будет одной и той же для всех лучей SX. Действуем с помощью всё тех же трёх пар подобных треугольников:

SAO S0 A0 O; SXS0

OP S0 ;

SS0 + S0 O

b A0 O S0 O

Величина b не зависит от луча SX, поэтому продолжения всех преломлённых лучей XY пересекутся в точке S0
мнимом изображении точки S. Теорема об изображении тем самым полностью доказана.

Вспомним, что для собирающей линзы мы получили аналогичные формулы (4.11
) и (4.15
). В случае a = f их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации a > f и a

А вот у формулы (4.18
) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника случай тут, как мы и сказали выше, имеется только один.

Если точка S не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой параллельно главной оптической оси (рис. 4.51
).

Рис. 4.52. Построение изображения точки S, лежащей на главной оптической оси

Соотношение (4.18
) даёт нам ещё один вариант формулы линзы. Сначала перепишем:

а потом разделим обе части полученного равенства на a:

Действительное изображение

Опти́ческое изображе́ние
— картина, получаемая в результате прохождения через оптическую систему световых лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали.

На практике часто меняют масштаб изображения предметов и проецируют его на какую-либо поверхность.

Соответствие объекту достигается, когда каждая его точка изображается точкой, хотя бы приблизительно. При этом различают два случая: действительное изображение и мнимое изображение.

Действительное изображение
создаётся, когда после всех отражений и преломлений лучи, вышедшие из одной точки предмета, собираются в одну точку.

Действительное изображение нельзя видеть непосредственно, но можно увидеть его проекцию, просто поставив рассеивающий экран. Действительное создаётся такими оптическими системами, как объектив (например, кинопроектора или фотоаппарата) или одна положительная линза .

Мнимое изображение
— такое, которое можно видеть глазом. При этом каждой точке предмета соответствует выходящий из оптической системы пучок лучей, которые, если бы продолжить их обратно прямыми линиями, сошлись бы в одной точке; возникает видимость, что пучок выходит именно оттуда. Мнимое изображение создаётся такими оптическими системами, как бинокль , микроскоп , отрицательная или положительная линза (лупа), а также плоское зеркало.

Во всякой реальной оптической системе неизбежно присутствуют аберрации , в результате чего лучи (или их продолжения) не сходятся идеально в одной точке, и кроме того, максимально близко сходятся не совсем там, где нужно. Изображение получается несколько размытым и геометрически не полностью подобным предмету; возможны и другие дефекты.

Пучок лучей, который расходится из одной точки или сходится в ней, называется гомоцентрическим. Ему соответствует сферическая световая волна. Задача большинства оптических систем — преобразовывать расходящиеся гомоцентрические пучки в гомоцентрические же, тем самым создавая мнимое или действительное изображение, чаще всего, в другом масштабе по отношению к предмету.

Стигматическое изображение (от др.-греч. στίγμα

— укол, рубец) — оптическое изображение, каждая точка которого соответствует одной точке изображаемого оптической системой объекта.

Стигматическое изображение не обязательно геометрически подобно изображаемому объекту, но если оно подобно, такое изображение называется идеальным. Это возможно лишь при условии, что в оптической системе отсутствуют или устранены все аберрации , и что возможно пренебречь волновыми свойствами света . Оптическую систему, которая создаёт идеальное изображение, называют идеальной оптической системой. Идеальными можно приближённо считать центрированные системы, в которых изображение получается с помощью монохроматических и параксиальных пучков света.

Изображение предмета, даваемого рассеивающей линзой

Рассмотрим построение изображений, которые можно получить с помощью рассеивающей линзы (рисунок 6).

Такая линза никогда не даст действительного изображения, оно всегда будет мнимым. Ведь лучи, проходящие через рассеивающую линзу, расходятся. Это значит, что они никогда не пересекутся в противоположной от расположения предмета стороне. Будут пересекаться продолжения световых лучей на той же стороне от линзы, где находится предмет.

Рисунок 6. Изображение предмета, даваемое рассеивающей линзой

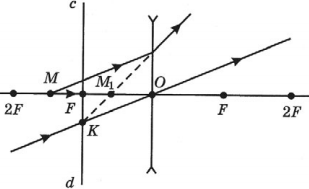
Рассмотрим чертеж. Из точки $A$ выходят два луча $AC$ и $AO$. Луч $AC$ достигает линзы и преломляется. Луч $AO$ после прохождения сквозь линзу не изменяет своего направления.

Из чертежа сразу ясно, что преломленные лучи не пересекутся. Значит, должны пересечься их продолжения. Продолжение первого преломленного луча пройдет через мнимый фокус по определению рассеивающей линзы. Продолжение луча второго преломленного луча совпадает с лучом $AO$.

Эти продолжения пересекаются в точке $A_1$ — мнимом изображении точки $A$. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим точки и получим изображение предмета $A_1B_1$.

{"questions":,"answer":}}}]}

Подтвердим вышесказанное опытом. Возьмем большую рассеивающую линзу и свечу. Свечу установим на подставке так, чтобы ее крайняя нижняя точка находилась на оптической оси линзы (рисунок 7).

Рисунок 7. Изображение предмета, даваемое рассеивающей линзой, в действительности

Смотря через линзу мы не увидим реальную свечу. Мы увидим ее мнимое, прямое и уменьшенное изображение $A_1B_1$. Все совпало с нашим чертежом.

Если мы начнем передвигать свечу относительно линзы, то увидим, что характеристики ее изображения будут сохраняться. Вне зависимости от положения свечи, ее изображение всегда будет мнимым, прямым и уменьшенным.

Прямолинейное распространение света

Закон распространения света:
свет в прозрачной однородной среде распространяется прямолинейно.

Экспериментальным доказательством прямолинейности распространения света является образование тени.

Тень – это область пространства, куда не попадает свет от источника.

Полутень – это область пространства, куда частично попадает свет от источника.

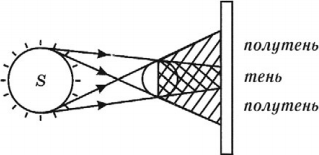
Если источник света точечный, то на экране образуется четкая тень предмета.

Если источник неточечный, то на экране образуется размытая тень (области тени и полутени).

Образованием тени при падении света на непрозрачный предмет объясняются такие явления, как солнечное и лунное затмения.

Построение изображений в линзах

Для построения изображения в линзах следует помнить:

1. луч, идущий вдоль главной оптической оси линзы, не преломляется;
2. луч, проходящий через оптический центр линзы, не преломляется;
3. луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
4. луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
5. луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
6. произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
7. произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.

Изображение, даваемое тонкой линзой, может быть действительным или мнимым.

Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.

Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.

Построение изображений точки, даваемых собирающей линзой

Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.

Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.

Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.

Если точка находится в фокусе линзы, то его изображение находится в бесконечности.

Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.

Построение изображений предмета, даваемых собирающей линзой

Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.

Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.

Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.

Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.

Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.

Построение изображений точки, даваемых рассеивающей линзой

В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.

Построение изображений предмета, даваемых рассеивающей линзой

Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.

Важно!
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние

Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.

При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.

Изображение отраженное во льду

Когда изображение отражается во льду, оно приобретает некую магическую и таинственную атмосферу. Отражение становится нереальным, и местами могут возникать искажения и перекосы, что создает интригующий и необычный эффект.

Охраняйте водные пространства оттаявшего льда бесконтрольного проникновения. Внимательно проверяйте пространство – наличие нефтепродуктов, газовых пород и других примесей. Ориентируйтесь на то, что лед несет не все, а слабые места его носимости могут быть непредсказуемо расположены. При проведении мероприятий в условиях замерзающей воды размещайте технику и оборудование на льду или об обледенелые поверхности так, чтобы они не ухудшали зимнюю экологию рек и водоемов.

В отличие от обычного отражения в зеркальной поверхности, отражение во льду обладает своими особенностями. Текстура льда, наличие трещин и бликов делают изображение более оригинальным и загадочным. В некоторых случаях, когда лед сильно треснул и деформировался, отражение может превратиться в настоящую калейдоскопическую картину.

Лед также может изменять цвет отражаемого изображения. Он может придать ему синеватый оттенок или отразить окружающую природу и облака, что создает гармоничное слияние между отражением и окружающей средой.

Природа постоянно создает нам удивительные зрелища, и отражение во льду является одним из них. Наблюдая за такими моментами, мы можем увидеть мир совершенно иными глазами и почувствовать его волшебство.