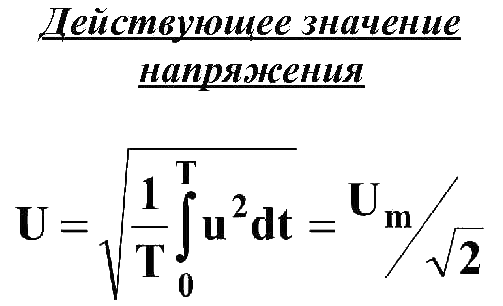Что такое мгновенное значение эдс?

Закон Ома для катушки индуктивности

Индукционное магнитное поле тормозит движение по проводнику свободных зарядов. Это причина дополнительного (индукционного) сопротивления. Оно зависит от индуктивности L, частоты сигнала:

где RL – индуктивное сопротивление.

Зависимость характеристик для участка цепи с катушкой индуктивности приобретает вид:

Катушка индуктивности имеет особенность: в ней колебания напряжения и скорости изменения заряда отличаются по фазе.

Колебания напряжения опережают колебания тока на четверть периода:

Разность между значениями функции sin для 2 колебаний называют сдвигом фаз. Для индуктивной катушки:

Для наглядности сдвиг фаз Δφ изображают в виде векторной диаграммы. Участок цепи, в котором возникает разность фаз между колебаниями тока, напряжения называют реактивной нагрузкой.

Переменный ток. Производство, передача и потребление электрической энергии

Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.

Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:

• мгновенное значение силы тока – i;

• мгновенное значение напряжения – u;

• амплитудное значение силы тока – Im;

• амплитудное значение напряжения –Um.

Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.

Активное сопротивление

Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ​\( R \)​. (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.

В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:

Мгновенное значение мощности: ​\( p=i^2R, \)​

среднее значение мощности за период: ​\( \overline{p}=\frac{I_m^2R}{2}. \)​

Действующим значением силы переменного тока ​\( I_Д \)​ называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:

Действующим значением напряжения переменного тока ​\( U_Д \)​ называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:

Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.

Индуктивное сопротивление

Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ​\( \pi/2 \)​. Колебания силы тока и напряжения происходят по закону:

Амплитуда силы тока в катушке:

где ​\( L \)​ – индуктивность катушки.

Индуктивным сопротивлением ​\( X_L \)​ называют физическую величину, равную произведению циклической частоты на индуктивность катушки:

Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.

Для цепи с индуктивным сопротивлением выполняется закон Ома.

Как рассчитать и использовать

Мгновенное амплитудное действующее значение тока или напряжения ЭДС является важным параметром при анализе электрических цепей. Это значение отражает силу тока или напряжения в определенный момент времени. Рассмотрим, как рассчитать и использовать это значение.

Расчет мгновенного амплитудного действующего значения:

Для расчета мгновенного амплитудного действующего значения тока или напряжения ЭДС необходимо выполнить следующие шаги:

1. Запишите уравнение, описывающее зависимость величины от времени. Например, для синусоидального источника напряжения уравнение имеет вид: U = U * sin(ωt + φ), где U — амплитудное значение напряжения, ω — угловая частота, t — время, φ — начальная фаза.
2. Подставьте значение времени t, для которого вы хотите рассчитать мгновенное амплитудное действующее значение.
3. Решите уравнение для получения значения I или U.

Использование мгновенного амплитудного действующего значения:

Мгновенное амплитудное действующее значение тока или напряжения ЭДС может быть использовано для решения различных задач, включая:

• Расчет мощности потребляемой или вырабатываемой схемой электрической энергии. Для этого необходимо умножить мгновенное амплитудное действующее значение тока на мгновенное амплитудное действующее значение напряжения и умножить результат на коэффициент мощности.
• Анализ стабильности и устойчивости электрической сети. Мгновенное амплитудное действующее значение тока и напряжения используется для определения перегрузок и неустойчивостей в сети и для принятия мер по их устранению.
• Диагностика и отладка электрических цепей. Мгновенное амплитудное действующее значение помогает выявить неисправности в цепи, такие как короткое замыкание или обрыв проводов.

Важно помнить, что мгновенное амплитудное действующее значение тока и напряжения является мгновенной величиной, и его значение изменяется в каждый момент времени. Поэтому при расчете и использовании необходимо учитывать специфику задачи и учитывать изменение значений в течение времени

Использование мгновенного амплитудного действующего значения тока и напряжения ЭДС в анализе и проектировании электрических цепей помогает обеспечить их эффективную работу, безопасность и надежность.

Действующее значение переменного тока. Характеристики переменного тока

Определение 1

Действующее или эффективное значение переменного тока – это значение переменного электрического тока равное величине постоянного тока, который проделает такую же работу, сопровождающуюся тепловым эффектом или электродинамическим эффектом, что и рассматриваемый переменный ток за время равное одному периоду переменного тока.

К основным характеристикам переменного тока относятся:

1. Амплитуда, являющаяся максимальным значением периодически изменяющегося тока.
2. Период, который является временем, в течении которого электрическим током совершается полный цикл изменений, после чего они повторяются в той же последовательности.
3. Частота, которая обратна периоду, то есть показывает количество завершенных циклов изменений за единицу времени.
4. Мгновенное значение, являющееся значением переменного тока в конкретный момент времени.
5. Угловая скорость или угловая частота, которая характеризуется углом поворота рамки за единицу времени.

Статья: Действующее и среднее значение переменного тока

Найди решение своей задачи среди 1 000 000 ответов

В современной литературе обычно используется математическое определение действующего значения переменного тока, которое звучит следующим образом: действующее значение переменного тока — среднеквадратичное значение переменного тока. Таким образом эта величина рассчитывается по следующей формуле:

Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ

Существует пять типичных случаев переменного электрического тока:

1. Синусоида.
2. Прямоугольная форма.
3. Треугольная форма.
4. Трапециевидная форма.
5. Дугообразная форма.

Для синусоидального тока формула для расчета действующего значения выглядит следующим образом:

Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ

где Im — амплитудное значение тока.

Для электрического тока, который имеет форму однополярного прямоугольного импульса используется следующая формула для расчета действующего значения.

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

где D — коэффициент заполнения.

Если коэффициент заполнения равен 0,5, то есть ток имеет форму однополярного меандра, то формула выглядит так:

$I = Im* √0.5 = 0.707*Im$

В том случае, когда у тока форма двуxполярного меандра, то:

$I = Im$

Для токов пилообразной и треугольной формы расчет действующего значения осуществляется по формуле:

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Посредством разбивки периода на отрезки действия максимального значения, положительного фронта и отрицательного фронта, получается формула для расчета действующего значения переменного тока трапециевидной формы:

Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ

где: t1, t2, t3 — соответственно продолжительность положительного фронта, действия максимального значения и отрицательного фронта; Т — длительность полного периода.

Для тока, который имеет форму дуги или половины окружности, формула для расчета действующего значения имеет следующий вид:

Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ

Для измерения тока в цепях переменного тока большинство электроизмерительных приборов, таких как вольтметры и амперметры, градуируются таким образом, чтобы показания соответствовали эффективному значению переменного тока или напряжения.

Как найти значение амплитуды напряжения

Все мы знаем, что дома у нас в розетках напряжение 220 В. Но не все знают, что это за напряжение. Давайте разберемся с этой ситуацией.

Для упрощения рассматриваемого примера мы предположим, что тип напряжения – синусоида, которая представляет собой переменное напряжение (изменяющееся от положительного к отрицательному с определенной периодичностью).

Рисунок 1 – Тип переменного напряжения

На рисунке 1 показана форма идеального синусоидального напряжения с одним периодом Т. Существует несколько значений напряжения, о которых обычно говорят и которые используются, рассматриваются:

Значение амплитуды напряжения (U m ) – это максимальное мгновенное значение напряжения, т.е. амплитуда синусоидальной волны.

Сейчас правильнее говорить о токе.

Среднеквадратичное значение переменного тока – это количество постоянного тока, которое может совершить ту же работу (тепло).

Отн.м.с. значение напряжения (U) обозначается латинской буквой без индекса, в литературе также можно встретить термин отн.м.с. значение напряжения.

Для периодически изменяющегося сигнала среднеквадратичное значение напряжения находится в период T:

Сведем формулу к простой форме, взяв в качестве переменного сигнала синусоиду. Между этими двумя параметрами существует взаимосвязь, которая выражается формулой:

Это означает, что значение амплитуды в 1,414 раза больше эффективного значения.

Вернемся к бытовым розеткам 220 В. Это среднеквадратичное значение напряжения, которое можно измерить с помощью тестера. Определим значение амплитуды его напряжения:

Среднее значение синусоидального тока, напряжения будет равно нулю. Поэтому, говоря о среднем значении переменного тока, рассматривайте его как половину периода.

Примечания

На рисунке 1 показана идеальная форма сетевого напряжения. Она описывается мгновенными значениями. Um – амплитуда (максимальное мгновенное значение). Но работу в электрооборудовании выполняет среднеквадратичное (эффективное) значение, величина которого находится по формуле, приведенной в статье. Я только что вывел приблизительную функцию, которая описывает вид напряжения, вот график:

Теперь подставим полученное в формулу для расчета эффективной стоимости:

Из формулы видно, что функция дает интеграл, или поле, и здесь не имеет значения, какой знак (+ или -) имеет напряжение.В сети есть “Фаза” и “Ноль”, первая имеет положительный потенциал по отношению к земле, т.е. на ней присутствует напряжение 220В, а ноль – это просто “провод”, пока вы не подключите прибор, по нему не течет ток. Включите прибор: ток протекает от фазы через прибор до нуля. Проверьте по индикатору, “все еще горит”, как выполняется работа по эффективному значению. Поставьте диод перед индикатором, он будет работать только на полволны, и вы заметите мерцание.

Читайте далее:

• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• Трехфазные электрические цепи; Студопедия.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Значение переменного тока (ЭДС, напряжения), соответствующее любому моменту времени, называется его мгновенным значением; Студопедия.
• Шаговые двигатели: свойства и практические схемы управления. Часть 2.
• Среднеквадратичное значение переменного тока следующее. Каково среднеквадратичное значение переменного тока?.
• Механические колебания и волны; FIZI4KA.

Взаимоиндукция

Если собрать модуль из двух катушек, в определенных условиях можно наблюдать явление взаимной индукции. Элементарное измерение покажет, что по мере увеличения расстояния между элементами уменьшается магнитный поток. Обратное явление наблюдается по мере уменьшения зазора.

Чтобы находить подходящие компоненты при создании электрических схем, необходимо изучить тематические вычисления:

• можно взять для примера катушки с разным количеством витков (n1 и n2);
• взаимоиндукция (M2) при прохождении по первому контуру токаI1 будет вычислена следующим образом:

после преобразования этого выражения определяют значение магнитного потока:

для расчета эдс электромагнитной индукции формула подойдет из описания базовых принципов:

E2 = – n2 * ΔF/ Δt = M 2 * ΔI1/ Δt

При необходимости можно найти по аналогичному алгоритму соотношение для первой катушки:

E1 = – n1 * ΔF/ Δt = M 1 * ΔI2/ Δt.

Следует обратить внимание, что в этом случае значение имеет сила (I2) во втором рабочем контуре

Ответ

Проверено экспертом

Речь идём о переменном токе.

Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.

Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :

Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):

Обозначается действующее значение или без иднекса или с индексом «д»:

(только русское «д»).

Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении

Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.

Среднее значение величин (-//-) -среднее арифметическое значение величины за полпериода.

Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.

Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

Переменный электрический ток

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток.

Переменный электрический ток — это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,

где u – мгновенное значение напряжения, U_m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,

где φ_c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Линейное и фазное напряжения – разность и соотношение

Напряжение – это разность потенциалов между двумя точками в пространстве. Он измеряется в вольтах. Например, напряжение между плюсом и минусом батарейки составляет 1,5 вольта, а между поверхностью земли и грозовой тучей – миллионы вольт!

Все мы знаем, что напряжение переменного тока в нашей розетке составляет 220 – 230 вольт. Трехфазная розетка, с другой стороны, имеет напряжение 380 вольт. Разница в том, что в первом случае мы получаем фазное напряжение, а во втором – линейное. Итак, что такое линейное напряжение, что такое фазное напряжение и какова взаимосвязь между ними? И по какой причине именно такие соотношения.

Электроэнергия передается от электростанций к домам и предприятиям по высоковольтным линиям (в нашей стране – 50 Гц). В трансформаторных подстанциях высокое напряжение понижается и распределяется по потребителям. Но если у вас в квартире однофазная сеть (следует отметить, что в последние годы у бытовых потребителей появилась возможность подключения к трехфазной сети), а на заводе – трехфазная, давайте разберемся, в чем разница.

Среднеквадратичное и амплитудное напряжение

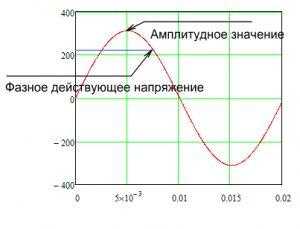
Когда мы говорим 220 или 380 вольт, мы имеем в виду среднеквадратичное значение напряжения, или эффективное напряжение. Фактически, амплитудное значение переменного напряжения всегда больше, чем фазное значение Umf или линейное значение Uml. Для синусоидального напряжения его амплитуда равна квадратному корню из 2-кратного среднеквадратичного значения (1414 раз).

Отсюда следует, что фазное напряжение 220 В соответствует амплитуде 310 В, а для сетевого напряжения 380 В амплитуда составит 537 В. Конечно, на практике напряжение в розетке часто не совсем 220 В, оно может быть выше или ниже, но оно должно быть в пределах допустимых параметров.

Что такое фазное напряжение в сети переменного тока?

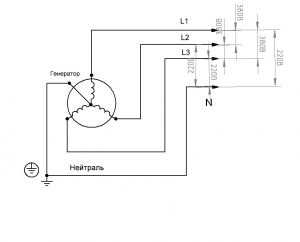
На электростанции обмотки генератора соединены звездой, т.е. концы X, Y и Z соединены в одной точке, которая называется нейтралью или нейтральной точкой генератора. Это известно как четырехпроводная трехфазная схема. Клеммы обмотки A, B и C подключаются к линейным проводам, а нейтраль или нейтральная точка подключается к нейтральной точке.

Напряжения между клеммами A и нейтральной точкой, B и нейтральной точкой, C и нейтральной точкой называются фазными напряжениями и обозначаются Ua, Ub и Uc, но поскольку сеть симметрична, мы можем просто записать Uf как фазное напряжение.

Линейное напряжение трехфазной сети

Действующие напряжения между клеммами A и B, между клеммами B и C, между клеммами C и A называются линейными напряжениями, т.е. это напряжения между линейными проводниками трехфазной сети. Они обозначаются как Uab, Ubc, Uca, или вы можете просто написать Ul.

Напряжение в наших электросетях составляет примерно 380 вольт. Соотношение между фазным и линейным напряжением в любой трехфазной сети с заземленным нейтральным проводником равно 1,732, что является квадратным корнем из 3. Хотя фактическое напряжение в сети может изменяться в диапазоне, зависящем от нагрузки, соотношение между фазным и линейным напряжением остается неизменным.

Напряженность электрического поля определяет, сколько энергии в нем запасено. Напряжение равно энергии, необходимой для перемещения заряда из одной точки в другую, деленной на величину этого заряда. В случае электрического поля энергия необходима, поскольку, согласно закону Кулона, на заряд действует сила, пропорциональная величине заряда. Таким образом:

Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока

Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p). Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е _m, напряжения — U _m, тока — I _m.

Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.

Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.

Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.

По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:

E _m = E · 1,41; U _m = U · 1,41; I _m = I · 1,41;

Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.

Под средним значением понимают среднеарифметическое ее значение за половину периода.

Переменный электрический ток

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток.

Переменный электрический ток — это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,

где u – мгновенное значение напряжения, U_m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,

где φ_c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Формула действующего значение тока

Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:

• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.

• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.

• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.

• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.

• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.

Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:

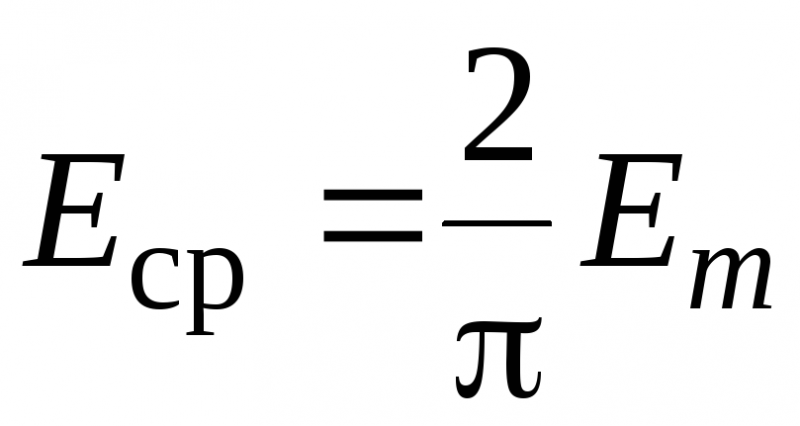
Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.

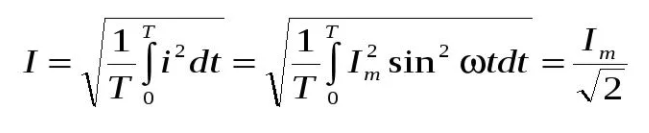
Схожим образом обозначаются эффективные значения напряжения и ЭДС.

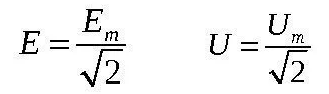
Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.

Закон Ома.

Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm,  1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.

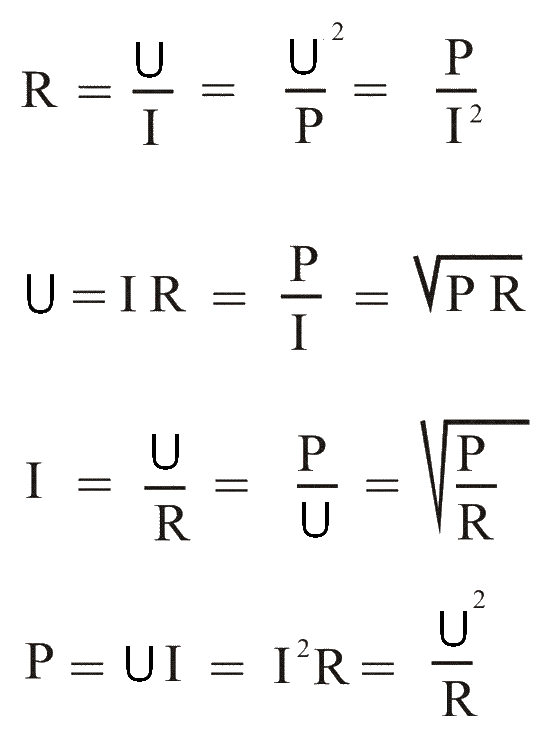
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.

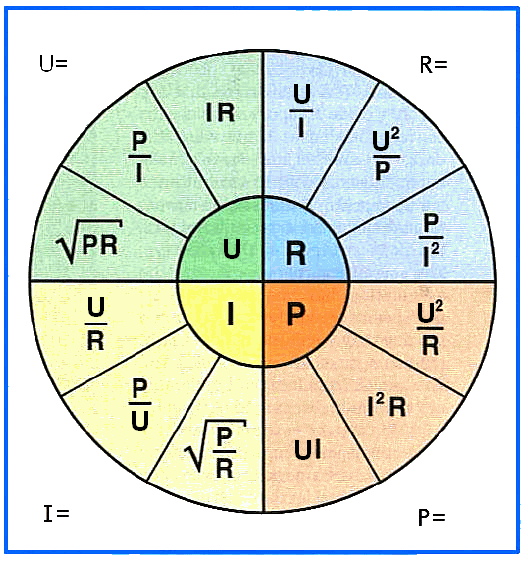
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.
Выглядит она следующим образом:

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

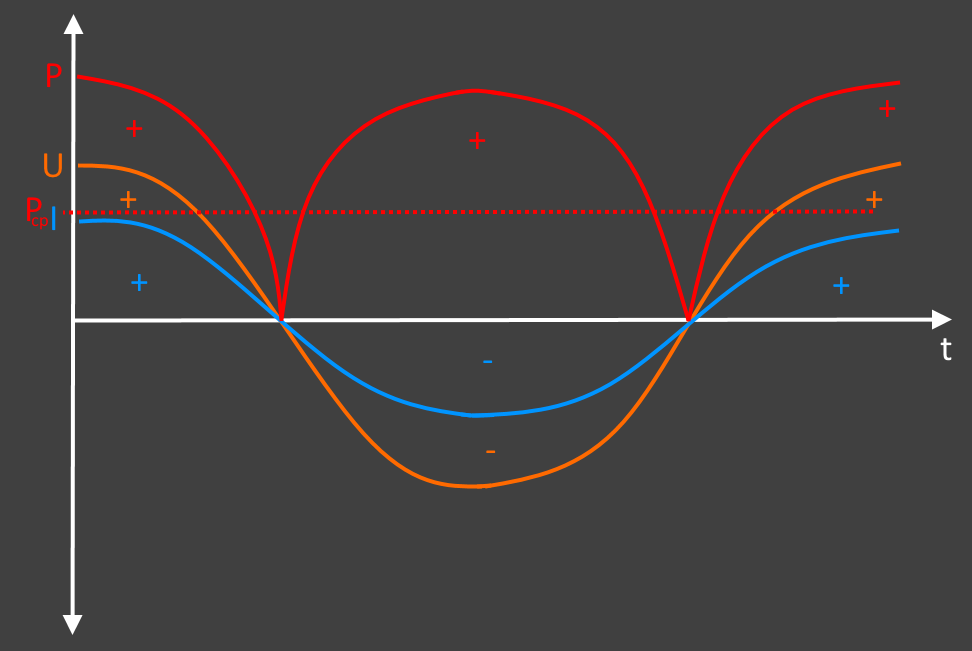
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Определение действующего напряжения

Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.

Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.

Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

Общая формула расчета действующего напряжения произвольной формы следующая: