Общее положение
Субъектам экономики (домашним хозяйствам, компаниям и государству с его подразделениями, таким как государственное управление, государственные и муниципальные предприятия) необходимо рационально обращаться с ограниченными ресурсами (рациональный принцип). Это подразумевает наличие производительности как суммы производственных показателей экономических субъектов и их поведенческих моделей, обычно связанных с производственным процессом и производственными факторами. Измеряется по рациональному принципу, т.е. все считается продуктивным, где используемые ресурсы находятся в благоприятном соотношении с достигнутым эффектом. Продуктивность тесно связана с конструктивностью и противопоставляется деструктивности.
Задачи «на совместную работу».
Задачи «на работу» делятся на два вида: на производительность труда и на производительность различных механизмов (труб, насосов и т. д.). Такие задачи часто вычисляются по формуле:
А=P?t
где P – производительность труда, т. е. часть работы, выполняемая в единицу времени;
t – время, необходимое для выполнения всей работы.
Пусть P?t=1 – взаимообратные величины, т. е. вся работа А=1, следовательно:
P=A/t=1/t t=A/P=1/P
Решим задачу на производительность труда.
Задача №1.
Три каменщика разной квалификации выложили кирпичную стену, причём первый каменщик работал 6 часов, второй – 4 часа, а третий – 7 часов. Если бы первый каменщик работал 4 часа, второй – 2 часа и третий – 5 часов, то было бы выполнено 2/3 всей работы. За сколько часов каменщики закончили бы кладку, если бы они работали вместе одно и то же время?
Решение.
Решим эту задачу путём составления системы уравнений.
Пусть х – скорость выполнения работы первого каменщика, y – второго, z – третьего. Всю работу примем за 1. Составим систему уравнений по условию задачи:
6x+4y+7z=1 (1)
4x+2y+5z=2/3 (2)
Надо найти t=A/P, то есть 1/(x+y+z)
Умножим (2) на -2 и сложим почленно с (1). Получим:
x=1/6-3z/2
Затем умножим (2) на -1,5 и сложим почленно с (1). Получим:
y=0,5z
Следовательно, подставим в искомое выражение полученные значения для x, y, z 1/(x+y+z)=1/(1/6-3z/2+z/2+z)=1/(1/6)=6.
В итоге получим 6.
Ответ: каменщики выполнят эту работу за 6 часов.
Мы решили эту задачу путём составления систем уравнений.
Задачи «на работу» сложны тем, что в них абстрактное понятие «работа» приобретает различное конкретное содержание. В первой задаче работа выражалась в виде производительности труда каменщиков. В следующей задаче мы рассмотрим случай, в котором идёт речь о работе по наполнению бассейна.
Задача №2.
При одновременной работе двух насосов разной мощности бассейн наполняется водой за 8 часов. После ремонта насосов производительность первого из них увеличилась в 1,2 раза, а второго – в 1,6 раза, и при одновременной работе насосов бассейн стал наполняться за 6 часов. За какое время наполнится бассейн при работе только первого насоса после ремонта?
Решение.
Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Следовательно, 1/x — производительность первого насоса до ремонта, а 1/y — производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1, т.е. 8/x+8/y=1.
1,2(1/x) — производительность первого насоса до ремонта, а 1,6(1/y) — производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1, т.е. 7,2/x+9,6/y=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
Ответ: 10 ч.
Вывод: в результате решения задач двух разных видов мы выяснили, что все задачи на работу решаются по одной общей формуле (А=P?t) и в большинстве случаев решаются путём составления систем уравнений.
Расчет
Общая производительность на предприятиях определяется по следующей формуле:
Производительность=\frac{Количество\;продукции\;на\;выходе}{Количество\;ресурсов\;на\;входе}.
Выходные данные задаются в виде количества за единицу времени, то есть рассматриваются как текущее количество. Входными данными также может быть размер потока, например количество рабочих часов в году (рабочее время) или амортизация за один год. Это также может быть размер запаса, например, среднее количество людей в год или средний запас капитала в год.
Поскольку производимые товары / услуги имеют очень разные виды, и состав производства различных товаров может изменяться со временем, необходимо оценивать различные товары, чтобы дать общий объем производства в виде одномерного размера. Для этого товары оцениваются по рыночным ценам, если таковые существуют. Товары, для которых нет рыночных цен, оцениваются по себестоимости. Кроме того, чистые изменения цен исключаются из результатов с использованием процедур корректировки цен. Одним из методов является расчет в постоянных ценах базового года.
Та же самая проблема оценки возникает и с капиталом, поскольку основной капитал состоит из разных товаров. С другой стороны, в качестве труда используются физические величины, такие как количество занятых или количество рабочих часов.
Производительность можно подразделить в соответствии с различными факторами производства:
Производительность\;труда=\frac{Количество\;продукции}{Использованное\;рабочее\;время}.
Производительность\;машин=\frac{Количество\;продукции}{Количество\;использованных\;машино-часов}.
Производительность\;материалов=\frac{Количество\;продукции}{Количество\;использованного\;материала}.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.
Примеры сил:
ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Задача № 2
А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.
Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.
Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?
Шаг первый: вводим переменные
Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.
Шаг второй: составляем и решаем уравнение
Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:
\
\
Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.
Теперь необходимо записать сумму:
\
Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:
\
\
Подставляем найденное значение $y$ в нашу формулу и получаем:
\
Находим производную этой конструкции:
\
Вновь приравниваем полученное выражение к нулю:
\
\
\
\
\
\
\
Шаг третий: находим максимальное значение функции
Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:
\
Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:
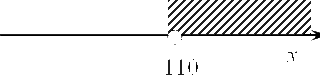
Давайте подставим:
${S}’\left( 220 \right)=1-\frac{2\cdot 220}{\sqrt{60500-{{220}^{2}}}}=1-\frac{440}{\sqrt{60500-48400}}=$
$=1-\frac{440}{\sqrt{12100}}=1-\frac{440}{110}=1-4=-3$
Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.
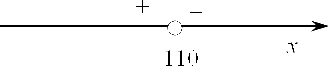
Итого 110 — точка максимума. Это является строгим обоснованием.
Теперь подставляем в выражение $x$ и $y$, которые мы нашли:
\
Ответ: 550 единиц товара.
Факторная производительность
При определении факторной производительности количество произведенных товаров устанавливается относительно входного количества фактора.
Эти статистически измеренные показатели производительности нельзя понимать как причинно-следственную связь в том смысле, что рост производительности труда, например, показывает, что работники становятся «более усердными», а снижение производительности капитала показывает, что капитал приносит все меньше и меньше. Скорее, рост производительности труда является результатом все большего использования «капитала» на одного работника, то есть фактически означает средства производства. Как правило, производительность труда увеличивается в долгосрочной перспективе, в то время как производительность «капитала» стагнирует или даже уменьшается.
В неоклассической теории предполагается, что производственные факторы вознаграждаются в соответствии с их производительностью, что не означает, что это происходит на практике. Это может быть связано с ошибками рынка и внешними факторами. С помощью статистически измеренных показателей производительности можно проверить, так ли это.
Производительность труда
Самый известный и наиболее используемый вид производительности — производительность труда. Это происходит из-за того, что объем затраченного труда определить легче, чем, например, износ или накопленный капитал, то есть машин, зданий и (в случае макроэкономической производительности) инфраструктурных объектов.
Экономическая формула производительности труда за час отработанного времени:
Производительность\;труда=\frac{ВВП_{реальный}}{Объем\;труда}=\frac{ВВП_{реальный}}{Ep+h}.
гдеВВП_{реальный} — реальный валовой внутренний продукт;Ep — количество занятых;h — количество часов, отработанных на одного работника.
Экономическая формула производительности труда на одного работающего:
Производительность\;труда=\frac{ВВП_{реальный}}{Ep+h},
или
Производительность\;труда=\frac{Результат}{Трудозатраты}.
Почасовая ставка получается из сравнения объема работ и отработанных часов:
Почасовая\;ставка=\frac{Объем\;продаж}{Рабочее\;время}.
Если объем продаж увеличивается с постоянным рабочим временем, продуктивная почасовая выработка также увеличивается и наоборот.
Производительность капитала
К примеру, Федеральное статистическое управление рассчитывает производительность капитала, сравнивая валовой внутренний продукт в постоянных ценах (последний раз в 1995 году) с запасом капитала. Последний показатель представляет собой валовые основные средства, также рассчитанные в постоянных ценах.
Добавление различных типов капитала к общему капиталу основано на сомнительных допущениях, которые подвергались критике в ходе спора о капитале.
Эмпирические выводы
Согласно данным Организации экономического сотрудничества и развития (ОЭСР), на июнь 2005 г., получены следующие результаты:
- В странах ОЭСР, то есть в промышленно развитых странах, потенциальное производство (производство при нормальном использовании основного капитала) в среднем за год увеличивалось на 2,9% в период с 1983 по 1992 год. Это несколько замедлилось до среднегодового значения в 2,6% с 1993 по 2002 год.
- Занятость росла в среднем за год на 2,4% и 1,1%. Таким образом, рост занятости замедлился в ОЭСР.
Что касается производительности труда, это приводит к росту примерно на 0,5% в первом и 1,5% во втором. Поэтому рост производительности труда ускорился. - Основной капитал вырос на 3,7% и 3,1% в среднем за год, т.е. быстрее, чем производство. В результате производительность капитала снизилась, в среднем за год с 0,8% в период с 1983 по 1993 год и на 0,5% в период с 1993 по 2002 год.
- Как правило, производительность труда увеличивается в среднесрочной и долгосрочной перспективе, а производительность капитала имеет тенденцию к снижению, как здесь, в странах ОЭСР. Заметным исключением являются Соединенные Штаты, для которых ОЭСР сообщает о среднегодовом росте производительности капитала на 0,1% в период с 1983 по 1992 год, а также на 0,1% в период с 1993 по 2002 год.
- Долгосрочное снижение производительности капитала является проблематичным, поскольку это означает, что долгосрочная рентабельность капитала может поддерживаться только в том случае, если доля трудовых доходов в ВВП уменьшается.
Задачи на совместную работу
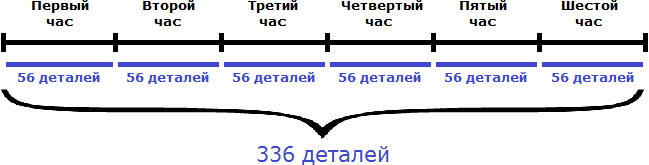
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
A = 1
Производительность первого мастера будет выражáться дробью . То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
А производительность второго мастера будет выражáться дробью . То есть за одну минуту он покрасит одну тридцатую часть забора:
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
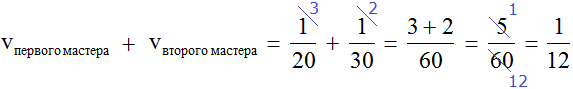
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят часть забора.
Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
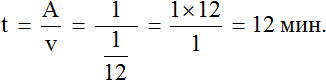
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
A = 1
Тогда первый рабочий за один час может выполнить часть работы, а второй рабочий часть работы. А вместе за один час они могут выполнить часть работы
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
Остальную часть работы, а именно работы заканчивал один второй рабочий:
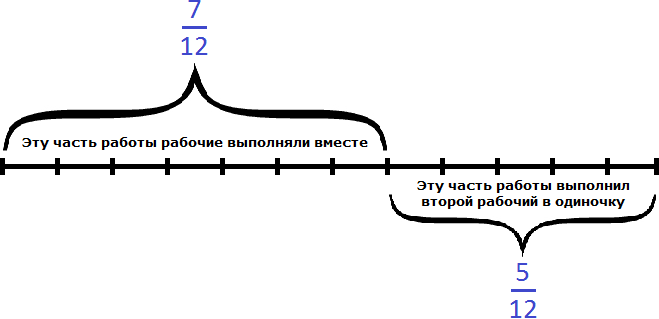
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна , переменная v —
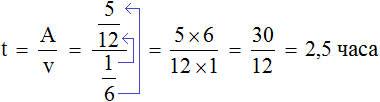
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
2 + 2,5 = 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
A = 1
Тогда первая труба за один час выполнит часть работы, а вторая труба — часть работы. Работая вместе за один час они выполнят часть работы:
Определим время за которое обе трубы наполняют бассейн, работая вместе:
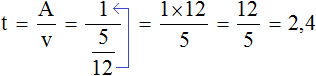
2,4 это два целых часа и четыре десятых часа
2,4 = 2 ч + 0,4 ч
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Предельная производительность
С точки зрения экономики предельная производительность также представляет собой интерес:
\frac{\partial x}{\partial r_i}.
Это указывает, насколько увеличивается выходной сигнал, когда входной коэффициент увеличивается на одну единицу, тогда как другие факторы остаются постоянными. Например, предельная производительность труда может быть измерена по количеству продукции, которая увеличивается, когда добавляется один дополнительный час работы. Предельная производительность представляет особый интерес, потому что, согласно теории, она определяет рыночную цену для фактора на совершенных факторных рынках.
В большинстве случаев предполагается положительная, но снижающаяся предельная производительность, то есть при увеличении затрат выпуск будет увеличиваться. Однако темп роста уменьшается по мере увеличения начального уровня ввода факторов производства.
Математически предельная производительность фактора может быть определена как частная производная производственной функции в соответствии с этим фактором.
FAQ — 💬
Как рассчитать производительность труда на одного работника?
Для вычисления производительности труда одного работника применяется та же формула: П = V : T, где П – производительность труда одного работника, V – количество единиц продукции, T –продолжительность периода.
Как по формуле найти производительность?
Как определить производительность труда: формула расчета Выработка или производительность труда одного работника (В) вычисляется как объем продукта (Оп), произведенного работником (Р) за единицу времени по формуле В = Оп/Р.
Как определить производительность?
Для нахождения производительности предусмотрено следующее правило: Чтобы найти производительность, надо выполненную работу разделить на время работы. где v — производительность, A — выполненная работа, t — время работы.
В чем измерить производительность труда?
Производительность труда измеряется количеством продукции, выпущенной работником за единицу времени. Обратная величина — трудоёмкость — измеряется количеством времени, затрачиваемым на единицу продукции.
Как рассчитать выработку на 1 человека?
Чтобы определить выработку на одного работающего или на один чел. -час в стоимостном выражении, надо разделить объем СМР на численность основного персонала, который выполнял эти работы, или на количество отработанных человеко-часов.
В чем разница между производительностью труда и выработкой?
Производительность труда – это мера результативности, эффективности труда человека. Производительность труда выражается двумя показателями: выработкой одного работника и трудоемкостью единицы продукции. Выработка – это объем продукции, произведенный одним работником в единицу времени (час, день, месяц, год).
В чем разница между производительностью труда и качеством труда?
Качество труда первично, так как оно представляет собой внутреннее сущностное свойство, а производительность – внешнее свойство как результат процесса труда, создающийся на основе роста его качества.
Какие показатели характеризуют производительность труда?
Производительность труда – это мера результативности, эффективности труда человека. Производительность труда выражается двумя показателями: выработкой одного работника и трудоемкостью единицы продукции.
Что такое работа и производительность?
Производительность труда показывает количество произведённого продукта или выполненных работ за единицу времени. Её можно рассчитать по отделу, подразделению и компании в целом, чтобы сравнить с отраслевыми показателями.
Как измеряется эффективность труда?
Производительность труда — эффективность труда в процессе производства. Измеряется количеством времени, затраченного на производство единицы продукции, или количеством продукции, произведенной в единицу времени. Обратная величина — трудоемкость — измеряется количеством времени, затрачиваемым на единицу продукции.
Что такое производительность труда простыми словами?
Производительность труда — показатель, который характеризует результативность труда человека, компании или всех работников в стране за единицу времени. Проще говоря, это объём работы, который выполняет сотрудник или целый отдел за какое-то определённое время.
Как определить производительность предприятия?
На предприятии производительность определяется через два базовых показателя: трудоемкость. Именно они наиболее целесообразны при оценке степени эффективности трудозатрат в единицу времени. Повышение производительности приводит к увеличению объемов производства и экономии на заработной плате.
Что такое объем производительности труда?
При проведении расчетов учитывать то, что объем производительности труда – это переменчивая величина, которая зависит не только от работников, но и от руководителя (владельца) компании: чем лучше условия труда на предприятии, тем выше и надежнее будет мотивация сотрудников и их производительность труда.
Как определить производительность труда персонала?
Важными показателями в производительности труда персонала являются следующие: Средний показатель выработки продукции за час – показывает количество изготовленной продукции за единицу времени – час. Берется только фактически затраченное время, не учитываются паузы или простои сотрудников.
Как решать задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
Пример №2
Первая труба заполняет бассейн за \( \displaystyle 6\) часов, а вторая – за \( \displaystyle 4\).
За какое время они заполнят бассейн, работая вместе?
Решение
Во-первых, давай придумаем аналогию с движением.
Придумал?
Бассейн – это путь. Допустим, из \( \displaystyle A\) в \( \displaystyle B\). Итак, первый автомобиль проезжает путь \( \displaystyle AB\) за \( \displaystyle 6\) часов, второй – за \( \displaystyle 4\).
А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.
Если двигаться параллельно, то каждый проходит весь путь самостоятельно
А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!. Тогда что нас просят найти? Время, через которое они встретятся
Тогда что нас просят найти? Время, через которое они встретятся.
Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.
Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: \( \displaystyle {{P}_{1}}=\frac{A}{{{t}_{1}}}=\frac{A}{6}\). А второго? \( \displaystyle {{P}_{2}}=\frac{A}{{{t}_{2}}}=\frac{A}{4}\).
С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:\( \displaystyle P={{P}_{1}}+{{P}_{2}}\)То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: \( \displaystyle v={{v}_{1}}+{{v}_{2}}\).
Итак,
\( \displaystyle P={{P}_{1}}+{{P}_{2}}=\frac{A}{6}+\frac{A}{4}=\frac{5A}{12}\).
Тогда время, за которое с такой производительностью будет выполнена работа \( A\):
\( \displaystyle t=\frac{A}{P}=\frac{A}{\frac{5A}{12}}=\frac{12}{5}=2,4\) (ч)
Итак, правило:
Расчет уровня производительности труда
Производительность труда = общий выпуск / затраты на труд— Общий выпуск — количество товаров или услуг, произведенных за определенный период времени. Может измеряться как в количестве продуктов (физических единицах), так и в ВВП (стоимостные единицы).- Затраты на труд — количество затраченного труда, часы работы. Изменение уровня производительности труда может быть достигнуто за счет таких факторов, как технологический прогресс — внедрение новых технологий, автоматизация процессов, использование компьютерных систем. Инвестиции в образование и подготовку работников способствуют повышению их квалификации, умений и знаний, что помогает в целом улучшить их эффективность, как следствие, сократить затраты на труд.Оптимизация рабочих процессов и методов работы также может сократить временные и ресурсные затраты (к примеру, сокращение избыточных шагов и устранение «узких мест»).Немаловажную роль играет мотивация и поощрение работников: создание прозрачных стимулов помогает им оставаться продуктивными. Среди этих мер можно выделить как премии, поощрения, вознаграждения за достижение целей, так и психологический комфорт на рабочем месте. Создание комфортной и безопасной рабочей среды и эффективное управление производственными процессами также имеют значительное влияние на производительность труда.
Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике
Все, что нам нужно знать — это:
- Правило вычисления производных сложных функций.
- Правила решения несложных уравнений.
Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:
- ${{a}^{2}}\to a$ и ${{b}^{2}}\to 2b$ — как связано затраченное время с объемом выпущенного товара;
- $S=a+2b\to \max $ — суммарный объем товара находится по несложной формуле.
Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.
А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.
- Задачи на кредит с плавающим платежом
- Задачи с экономическим содержанием — основные формулы
- Тест к уроку «Что такое логарифм» (средний)
- Решение задач B12: №440—447
- Как решать задачу 18: графический подход
- Нестандартные задачи B2: кредит в банке
Экономические определения
В экономике и управлении бизнесом производительность понимается как ключевой показатель, который отражает количественное соотношение между тем, что производится (выпуск), и средствами или факторами производства (ввод), используемыми в производственном процессе.
Чтобы достичь этого, данный выпуск (принцип минимума) может быть достигнут либо с наименьшим возможным входом, либо с максимально возможным выпуском (принцип максимума) с заданным входом. Таким образом, производительность также является конкретным выражением рационального принципа. Соответствие производительности как принципу поведения также позволяет достичь цели максимизации прибыли или максимизации полезности. Поэтому между этими целями есть гармония.



























