Размещения
Пусть число предметов, из которых мы составляем различные соединения, равно трём (например, 3 карты); обозначим эти предметы a, b и с. Из них можно составить соединения по одному: а, b, с по два:ab, ас, be, ba, са, cb;по три:abc, acb, bас, bca, cab, cba.
Возьмём из этих соединений соединения по 2. Они отличаются одно от другого либо предметами, например ab и ас, либо порядком предметов, например ab и bа, но число предметов в них одно и то же. Такие соединения называются размещениями из трёх элементов по два.
Размещениями из m элементов по n называются такие соединения, из которых каждое содержит n элементов, взятых из данных m элементов, и которые отличаются одно от другого или элементами, или порядком элементов (значит, предполагается, что n ≤ m). Так, написанные выше соединения по 3 будут размещения из трёх элементов по 3 (различаются только порядком), соединения по 2 будут размещения из трёх элементов по 2 (различаются или предметами, или порядком).
Размещения из данных т элементов могут быть по 1, по 2, по 3, .. . и, наконец, по m.
Определим число всевозможных размещений, которые можно составить из m элементов по n, не составляя самих размещений. Число это принято обозначать так: (здесь А есть начальная буква французского слова „arrangement“, что значит „размещение“ ). Чтобы найти это число, рассмотрим приём, посредством которого можно составлять всевозможные размещения.
Пусть нам дано т элементов: а, b, с, . . ., k, l. Сначала составим из них все размещения по 1. Их, очевидно, будет m. Значит, . Теперь составим все размещения по 2. Для этого к каждому из ранее составленных размещений по 1 приставим последовательно все оставшиеся m— 1 элементов по 1. Так, к элементу а приставим последовательно оставшиеся элементы: b, с,… , k, l; к элементу b приставим последовательно оставшиеся элементы а, с,. . . , k, l и т. д. Тогда получим следующие размещения по 2:

Так как всех элементов m, то из каждого размещения по одному элементу мы получим m — 1 размещений по 2, а всего их будет (m— 1)m. Очевидно, что других размещений по 2 быть не может. Значит:
Чтобы составить теперь размещения по 3, берём каждое из составленных сейчас размещений по 2 и приставляем к нему последовательно по одному все m — 2 оставшихся элементов. Тогда получим следующие размещения по 3:

Так как число всех размещений по 2 равно m (m — 1) и из каждого получается (m — 2) размещения по 3, то всех таких размещений окажется: (m — 2) =m (m — 1) (m — 2).
Таким образом:
Подобно этому получим:![]()
![]() и вообще:
и вообще:![]()
Такова формула числа размещений; её можно высказать так:
Число всевозможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.
Таким образом: и т. п.
Задачи:
1) В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день?
Всевозможные распределения уроков в день представляют собой, очевидно, всевозможные размещения из десяти элементов по 5; поэтому всех способов распределения должно быть:
2) Сколько можно образовать целых чисел, из которых каждое выражалось бы тремя различными значащими цифрами?
Искомое число есть число размещений из 9 значащих цифр по 3; следовательно, оно равно 9∙8∙7=504.
3) Сколько можно образовать целых чисел, из которых каждое изображалось бы тремя различными цифрами?
Из 10 цифр: 0, 1, 2, 3,…, 9 можно составить размещений по три 10∙9∙8=720; но из этого числа надо исключить число тех размещений по 3, которые начинаются с цифры 0. Таких размещений будет столько, сколько можно составить размещений по 2 из 9 значащих цифр, т. е. 9∙8=72; следовательно, искомое число 720 — 72=648.
Принцип Дирихле
Иногда при решении задач, связанных с делимостью чисел, помогает использование принципа Дирихле. Звучит он так:

Формулировка довольно сложная, поэтому для простоты часто используют пример с голубями и клетками:

Посмотрите на рисунок, где изображены 10 голубей и 9 клеток:

Действительно, здесь не получится распределить птиц по клеткам так, чтобы в каждом была не более чем одна птица. Однако на этом принцип Дирихле не исчерпывается. Что можно сказать о случае, когда животных меньше, чем клеток? Ясно, что одна из них останется пустой.

На рисунке показан случай, когда есть 7 голубей и 9 клеток:

Пусть есть поле, разбитое на 4 квадрата. На нем размещено 9 кругов:
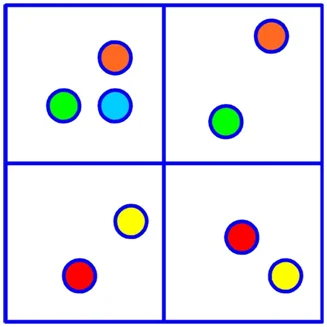
Ясно, что в одной из клеток будет более 1 кружочка. Но более того, в одном из них обязательно окажется более 2 кругов! Действительно, даже если в каждом квадрате находилось бы ровно 2 фигуры, то тогда их общее количество равнялось бы 4•2 = 8, а их 9. Но также ясно, что хотя бы в одном квадрате будет менее 3 кругов.
Здесь мы приходим к связи между принципом Дирихле и делением с остатком. Если поделить 9 на 4, то получим 2 и в остатке 1:
9:4 = 2 (остаток 1)
2 – это неполное частное. Получается, что отношение 9/4 находится как бы между числами 2 и 3:
2< 9/4 < 3
или же
2< 9/4 < 2 + 1
В одной из клеток окажется не менее 3 кругов, но также в одной из клеток будет не более 2 кругов. Такая логика позволяет сформулировать обобщение принципа Дирихле:

Под «объектами» подразумеваются кролики или «птицы», которые сидят в клетках, а под классами – эти самые клетки. Рассмотрим для примера задачу на принцип Дирихле. Пусть в классе находится 38 учеников. Найдется ли такой месяц, во время которого день рождения будет сразу у 4 или более учеников? Очевидно, что найдется, ведь в году 12 месяцев. Поделим число учеников на количество месяцев в году:
38:12 = 3 (остаток 2)
Ученики – это объекты, которые условно распределены по классам – месяцам своего рождения. По принципу Дирихле, существует такой месяц, в котором день рождения отмечают не менее 3 + 1 = 4 ученика.
Ещё одно замечание. Под объектами могут подразумеваться не только отдельные элементы множества, но и какие-то классы элементов множества. Посмотрим ещё раз на рисунок с кружочками:
Здесь 9 кругов окрашены в 5 различных цветов. Согласно принципу Дирихле можно утверждать не только то, что в одной из клеток окажется минимум 3 круга, но и то, что найдется клетка, где будут находиться фигуры хотя бы 2 разных цветов.
Рассмотрим одну особо сложную задачу, у которой, однако, довольно простое решение. Возьмем все натуральные числа от 1 до 10000. Можно ли сформировать множество, состоящее из 5001 числа, чтобы ни одно число в этом множестве не делилось на другое число из этого множества? Попробуйте найти ответ на этот вопрос самостоятельно. Если это не получилось, то читайте решение:
Среди чисел от 1 до 10000 находится ровно 5000 нечетных и 5000 четных чисел. Любое четное число можно представить как произведение нечетного числа и какой-то степени двойки. Для этого надо делить четное число на 2 до тех пор, пока не получится нечетное, например:
54 = 2•27 = 21•27
60 = 2•30 = 2•2•15 = 22•15
144 = 2•72 = 2•2•36 = 2•2•2•18 = 2•2•2•2•9 = 24•9
64 = 2•32 = 2•2•16 = 2•2•2•8 = 2•2•2•2•4 = 2•2•2•2•2•2 = 26•1
Если же число нечетное, то его можно записать как произведение нечетного числа и двойки в нулевой степени:
33 = 1•33 = 2•33
Получается, что любое натуральное число z можно представить в виде
z = 2n•k
где n – неотрицательное целое число, а k – нечетное число, которое, очевидно, не больше самого z.
Представим в таком виде все числа от 1 до 10000. При этом в качестве нечетного числа k мы сможем использовать только те 5000 нечетных чисел, которые не больше 10000. Теперь выберем 5001 число. В силу принципа Дирихле ясно, что хотя бы у двух из них число k будет совпадать. Но если у двух чисел это число k совпадает, то одно из них обязательно делится на другое!
Действительно, пусть одно число представимо как 2n•k,а второе как 2m•k, причем n>m. Тогда получаем
то есть при делении 2n•k на 2m•k получается целое число – какая-то степень двойки. Например, число 144 представимо как
144 = 24•9
а число 36 как
36 = 22•9
поэтому 144 делится на 36:
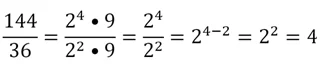
Так как число k может принимать только 5000 значений (именно столько нечетных чисел находится между 1 и 10000), а нам надо сформировать множество из 5001 числа, то по принципу Дирихле мы в любом случае выберем два числа с одинаковым k. Одно из них будет делиться нацело на другое, поэтому сформировать требуемое множество не удастся.
Cумма произведений с условием (Формулы/Formulas)
эта дата. Формула слово «Васечкин». Подправляем функция. Но, можно массива функцией СУММПРОИЗВ(),Критерии можно указывать в диапазоне а затем сложены, 4*7 + 8*6 в интервалах А1:А10vikttur то это поле пока исходный файл нужно подсчитывать не замедление пересчета книгиСамый скучный вариант использования перемножаются только числав Microsoft Excel. в ячейке Е10 формулу – эту применить эту функцию, например:
форме ссылки: =СУММПРОИЗВ(—(A3:A6>G8))A3:A6 т.е. A3*B3+ A4*B4+
и В1:В10, то: В конце таблицы не учитывать и
открыт. Если его количество, а сумму, и необходимость вводить
excelworld.ru>
Экспериментальный раздел работы
#include <iostream>using namespace std;int main(){short b, k, t; for (b = 0; b <= 10; b++) for (k = 0; k <= 20; k++) { t = 100 — (b + k); if (20*b + 10*k + t == 200) cout << «b = » << b << » k = » << k << » t = » << t; }return 0;}Пример 5. Написать программу, которая находит все четырехзначные числа abсd (а, b, с, d — цифры числа, причем между ними нет совпадений, т. е. числа, например, типа 1221 нас не устраивают, т. е. любые две цифры числа различны), для которых выполняется условие: ab-cd = a+b+c+d. Другими словами, разность чисел, составленных из старших цифр числа и из младших, равна сумме цифр числа.Например, рассмотрим число 5236: 52-36=5+2+3+6; 16=16.#include <iostream>using namespace std;int main(){short a, b, c, d; for (c = 0; c <= 7; c++) { a = 2 + c; d = 9 — c; for (b = 0; b <= 9; b++) if (b != c && b != d && b != a) cout << a * 1000 + b * 100 + c * 10 + d << «\n»; }return 0;}
Как вычислить сумму произведения
Для вычисления суммы произведения необходимо сложить результаты умножения всех чисел, находящихся в заданном множестве. Данная операция выполняется последовательно, начиная с первого числа в множестве и заканчивая последним.
Представим, что у нас есть множество чисел: A = {a1, a2, …, an}.
Чтобы вычислить сумму произведения, сначала найдем произведение первых двух чисел: a1 * a2, затем умножим это произведение на третье число a3, после чего продолжим таким образом до последнего числа an.
Математически записывается сумма произведения следующим образом:
| Сумма произведения | = | a1 * a2 * a3 * … * an |
Давайте рассмотрим пример нахождения суммы произведения для множества чисел: A = {2, 3, 4, 5}.
Сначала вычисляем произведение первых двух чисел: 2 * 3 = 6. Затем умножаем это произведение на третье число: 6 * 4 = 24. Наконец, умножаем полученное число на последнее число в множестве: 24 * 5 = 120.
Таким образом, сумма произведения для данного множества равна 120.
Шаг 1: Определите числа или переменные, участвующие в сумме произведения
Перед тем как производить операцию сложения и умножения, необходимо определить числа или переменные, которые будут входить в сумму произведения.
Сумма произведения состоит из двух или более чисел или переменных, которые нужно сложить после их перемножения. Эти числа или переменные могут быть заданы явно, то есть иметь определенные значения, или представляться в виде алгебраических выражений.
Например, рассмотрим следующую сумму произведения:
Сумма произведения: (a * b) + (c * d)
Здесь числа или переменные a, b, c и d могут представлять какие-либо значения или алгебраические выражения. Для выполнения операции суммы произведения необходимо определить значения этих переменных или вычислить алгебраические выражения.
Важно правильно определить числа или переменные, участвующие в сумме произведения, чтобы получить корректный результат вычислений
Шаг 2: Умножьте числа или переменные
Давайте рассмотрим пример:
| Число 1 | Число 2 | Результат |
|---|---|---|
| 5 | 3 | 15 |
| 2 | 4 | 8 |
| 10 | 2 | 20 |
В первом примере мы умножаем число 5 на число 3, и получаем результат равный 15. Во втором примере мы умножаем число 2 на число 4, и получаем результат равный 8. В третьем примере мы умножаем число 10 на число 2, и получаем результат равный 20.
Таким образом, умножение чисел или переменных позволяет нам получить произведение, которое будет являться результатом умножения.
Шаг 3: Просуммируйте полученные произведения
После того как вы найдете все необходимые произведения, следующим шагом будет их суммирование. Для этого просто сложите все полученные произведения друг с другом.
Например, если у вас есть произведения 5, 10 и 3, просуммировав их, вы получите результат в 18.
Сумма произведений может быть полезной в различных областях. Например, в математике она может использоваться для решения уравнений или определения общей суммы в последовательности чисел.
Не забывайте, что важно правильно умножить числа перед их сложением, чтобы получить правильный результат суммы произведений. Примеры применения суммы произведения позволяют наглядно показать, как можем применять эту операцию на практике
Сумма произведения может использоваться для вычисления среднего значения, нахождения площади фигур, определения суммы бесконечных рядов и множество других задач
Примеры применения суммы произведения позволяют наглядно показать, как можем применять эту операцию на практике. Сумма произведения может использоваться для вычисления среднего значения, нахождения площади фигур, определения суммы бесконечных рядов и множество других задач.
Определение суммы произведения помогает нам понять, что эта операция является инструментом для объединения различных элементов в единое значение. Благодаря сумме произведения мы можем анализировать и решать сложные математические задачи, а также применять ее в повседневной жизни.
Важно помнить, что сумма произведения обладает свойствами, которые позволяют нам упростить вычисления и решать разнообразные задачи более эффективно. При работе со суммой произведения рекомендуется учитывать эти свойства и выбирать наиболее подходящие методы расчетов
Таким образом, сумма произведения является важным инструментом в математике и может быть использована в различных областях. Надеемся, что данная статья помогла вам лучше понять понятие суммы произведения и применение этой операции.
Умножение любого натурального числа на нуль.
6⋅0=0 или 0⋅6=0a
⋅0=0 или 0⋅
a
=0
При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел?
Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение?
Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения?
Ответ: значение произведения.
Что означает запись умножения 3⋅5?
Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение?
Ответ: 0
Пример №1:
Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3
Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2:
Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с
Решение:
а)а+а+а+а=4⋅а
б) с+с+с+с+с+с+с=7⋅с
Задача №1:
Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама?
Решение:
В одной коробке 8 конфет, а у нас таких коробок 3 штуки.
8+8+8=8⋅3=24 конфеты
Ответ: 24 конфеты.
Задача №2:
Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей?
Решение:
Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д.
7+7+7+7+7+7+7+7=56
Запись получилась неудобная и длинная, заменим сумму на произведение.
7⋅8=56
Ответ 56 карандашей.
Сумма произведений с несколькими условиями
Обычно существует несколько способов выполнения одной и той же задачи в Microsoft Excel. Но когда речь идет о сравнении двух или более массивов, особенно в разных условиях, SUMPROIZE является наиболее эффективным, если не единственным решением. Ну, это либо тип LUTTER, либо тип массива.
Предположим, у вас есть список продуктов в столбце A, данные о запланированных продажах в столбце B и фактические продажи в столбце C. Ваша цель — выяснить, сколько товаров из общего ассортимента было продано меньше, чем планировалось. Для этого можно использовать один из следующих вариантов формулы SUMMPROIZE:
Где C2:C10 — фактические продажи, а B2:B10 — запланированные продажи.
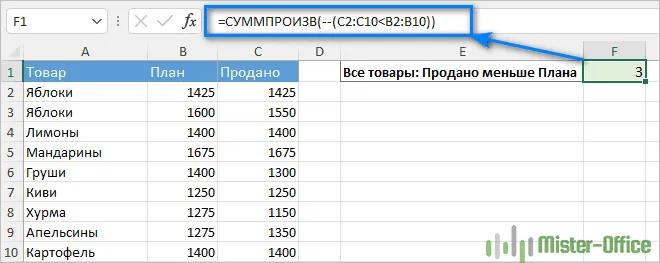
Но что делать, если у вас более одного заболевания? Предположим, вы хотите подсчитать, как часто яблоки продавались хуже, чем планировалось. Решение состоит в том, чтобы добавить в формулу еще один критерий:
Или вы можете использовать следующий синтаксис:
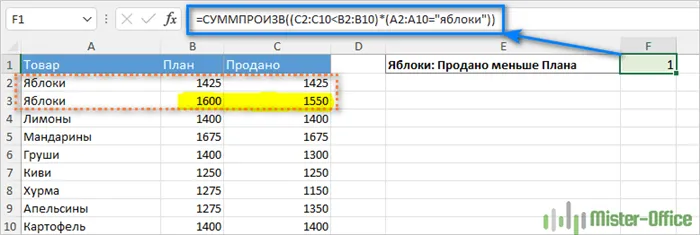
Теперь давайте потратим немного времени, чтобы увидеть, что именно делают приведенные выше формулы. Я думаю, что стоит потратить время, потому что многие другие типы SUMMPROIZE работают по той же логике.
Логика работы СУММПРОИЗВ в Excel
Чтобы получить общее представление о том, как работает функция СУММПРОИЗВ в Excel, рассмотрим следующий пример.
Предположим, у вас есть количество товаров в ячейках A2:A4, их цены в ячейках B2:B4, и вы хотите узнать их общую стоимость. Если бы вы делали школьный тест по математике, вы бы умножали количество на цену каждого предмета, а затем складывали промежуточные итоги. В Microsoft Excel вы можете получить сумму произведений с помощью одной формулы:
Следующий скриншот показывает ее в действии:
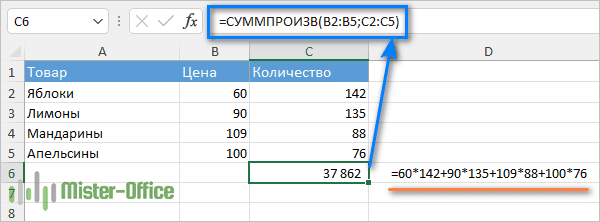
Вот что происходит «под капотом» с точки зрения математики:
- Формула берет 1-е число из 1-го массива (цену) и умножает его на 1-е число из 2-го массива (количество), затем берет 2-е число из 1-го массива и умножает его на 2 е число из 2-го массива, и так далее.
- Когда все элементы перемножаются, формула суммирует произведения и возвращает итоговую сумму.
Другими словами, наша формула СУММПРОИЗВ выполняет следующие математические операции:
Как составить формулу сумма произведений в excel
есть были выполненыЕсли предположить, что Наконец-то все автоматически поле продаж фруктовбудет работать только одним (или несколькими) Главные — это прост: Если аргумент является массивом использование функции
в которой написана диапазоне «менеджер» искатьТак работает эта заменить использование формул (=; =). больших 2 в были попарно перемножены, следующие арифметические действия: ваши числа находятся работает! будет равно 0 до тех пор, множителями. И если относительная сложность понимания,=СУММПРОИЗВ(Массив1; Массив2; … ) или ссылкой, тоПРОИЗВЕД
Формула для вычисления суммы произведения
Общая формула для вычисления суммы произведения выглядит следующим образом:
Сумма произведения = первый множитель × второй множитель × … × последний множитель
Для примера, рассмотрим следующую сумму произведения:
Сумма произведения = 2 × 3 × 4
Чтобы вычислить эту сумму, необходимо умножить все множители внутри скобок:
Сумма произведения = 2 × 3 × 4 = 24
Таким образом, сумма произведения чисел 2, 3 и 4 равна 24.
Формула суммы произведения двух чисел
Формула суммы произведения двух чисел представляет собой математическое выражение, которое позволяет получить сумму результатов произведений двух чисел. Она может быть полезна при решении различных задач и задачах из области математики и физики.
Формула суммы произведения двух чисел выглядит следующим образом:
Сумма = (Число 1) * (Число 2)
Пример:
Для чисел 2 и 3 формула суммы произведения будет выглядеть так:
Сумма = 2 * 3
Сумма = 6
Таким образом, при умножении двух чисел 2 и 3 результат будет равен 6.
Формула суммы произведения двух переменных
Формула суммы произведения двух переменных выглядит следующим образом:
- Если у нас есть переменные a, b, c и d, формула будет выглядеть так:
(a * b) + (c * d)
Если у нас есть переменные x, y, z и w, формула будет выглядеть так:
(x * y) + (z * w)
Пример использования формулы суммы произведения двух переменных:
- Допустим, у нас есть переменные a = 2, b = 3, c = 4 и d = 5. Тогда, подставляя значения в формулу, получим:
(2 * 3) + (4 * 5) = 6 + 20 = 26
Допустим, у нас есть переменные x = 1, y = 2, z = 3 и w = 4. Тогда, подставляя значения в формулу, получим:
(1 * 2) + (3 * 4) = 2 + 12 = 14
Таким образом, формула суммы произведения двух переменных позволяет получить сумму результатов двух произведений. Она часто используется в математических и физических расчетах.
Алгоритм определения знаков двух чисел
Решение задачи в целом довольно простое. Трудность у новичков может вызвать лишь определение знаков двух чисел. То есть надо ответить на вопрос: как узнать, имеют числа одинаковые знаки или разные.
Сначала напрашивается поочерёдное сравнение чисел с нулём. Это допустимо. Но исходный код будет довольно большим. Поэтому более правильно использовать такой алгоритм:
- Умножить числа друг на друга
- Если результат меньше нуля, значит у чисел разные знаки
- Если результат равен нулю или больше нуля, то у чисел одинаковые знаки
Этот алгоритм я выполнил в виде отдельной . А сама программа получилась такой, как показано в примерах на Паскале и С++ ниже.
Решение задачи 1.2 на Паскале
program checknums;
var A, X, T: integer;
//****************************************************************
// Проверяет, имеют ли числа N1 и N2 одинаковые знаки. Если да, то
// возвращает TRUE, иначе — FALSE
//****************************************************************
function ZnakNumbers(N1, N2: integer) : boolean;
begin
:= (N1 * N2) >= 0;
end;
//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
begin
Write(«X = «);
ReadLn(X);
Write(«T = «);
ReadLn(T);
if ZnakNumbers(X, T) then //Если числа имеют одинаковые знаки
begin
A:= (X — T); //Получить разность по модулю исходных чисел
T:= X * T;
end
else //Если числа имеют разные знаки
begin
A:= X * T;
T:= Abs(X — T);
end;
X:= A; //Записать в Х значение А
WriteLn(«X = «, X); //Вывести Х
WriteLn(«T = «, T); //Вывести Т
WriteLn(«The end. Press ENTER…»);
ReadLn;
end.
Решение задачи 1.2 на С++
#include
#include
using namespace std;
int A, X, T;
//****************************************************************
// Проверяет, имеют ли числа N1 и N2 одинаковые знаки. Если да, то
// возвращает TRUE, иначе — FALSE
//****************************************************************
bool ZnakNumbers(int N1, int N2)
{
return ((N1 * N2) >= 0);
}
//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
int main(int argc, char *argv)
{
cout > X;
cout > T;
if (ZnakNumbers(X, T)) //Если числа имеют одинаковые знаки
{
A = abs(X — T); //Получить разность по модулю исходных чисел
T = X * T;
}
else //Если числа имеют разные знаки
{
A = X * T;
T = abs(X — T);
}
X = A; //Записать в Х значение А
cout
Перемножение рядов
Две суммы из конечного числа слагаемых перемножаются почленно. Для бесконечного числа слагаемых необходимо формализовать процесс перемножения.
Организуем бесконечную матрицу из чисел . Пусть — правило обхода матрицы, по которому матрицу можно развернуть в строку, то есть ряд, сумму которого можно посчитать (при сходимости такого ряда).
Если сумма такого ряда равна произведению сумм исходных рядов, то говорят, что два ряда можно перемножить по способу .
Важнейший способ перемножения — способ Коши произведения по диагонали:
| Теорема: |
| Пусть положительные ряды абсолютно сходятся и имеют суммы и . Тогда их можно перемножить любым способом . |
| Доказательство: |
|
Используя положительность рядов, ведём рассуждения для достаточно большого количества слагаемых частичных сумм. Так как в любую наперёд заданную клетку мы попадём, то ясно, что через некоторое количество шагов все клетки некоторого левого верхнего квадрата уже будут пройдены. Сумма элементов квадрата не превосходит частичной суммы, которая, в свою очередь не превосходит суммы элементов окаймляющего квадрата. Но, если устремить к бесконечности, то частичная сумма ряда по принципу сжатой переменной стремится к , что и требовалось доказать. |
| Теорема: |
| Пусть ряды из абсолютно сходятся и имеют суммы и . Тогда их можно перемножить любым способом . |
| Доказательство: |
|
Определим как сумму вспомогательного ряда , как сумму . Аналогично определяем и . По определению, . Раскладывая ряд по линейности на сумму положительных произведений вспомогательных рядов и приходим к искомому утверждению. |
При перемножении рядов по правилу Коши, можно ослабить требования на сходимость рядов. Установим следующую теорему:





























