Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $\left$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:
\\]
Или вот так:
\
Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $\left$ и ${{a}_{ij}}$ возникает одна и та же проблема:
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
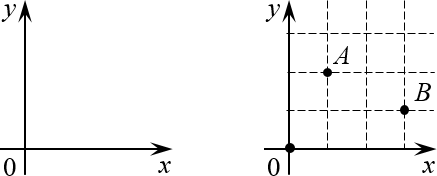Введение системы координат на плоскости
Помните её? У неё есть начало координат (точка $O=\left( 0;0 \right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=\left( 1;2 \right)$, $B=\left( 3;1 \right)$ и т.д.
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
Наложение системы координат на матрицу
Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:
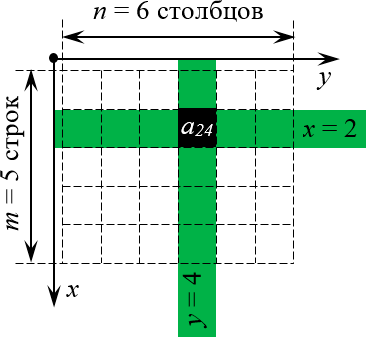Определение индексов в матрице
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Площадь, задаваемая векторами
Возьмем матрицу расширения, которая увеличивает площадь, заданную векторами.
|
1 |
i=np.array(1,) j=np.array(,1) Scale=np.array(3,, ,2) ax=plt.axes() plt.xlim(-0.5,4) plt.ylim(-0.5,4) plt.grid() ax.arrow(,,i,i1,width=0.02,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,j,j1,width=0.02,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,np.dot(Scale,i),np.dot(Scale,i)1,width=0.02,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.arrow(,,np.dot(Scale,j),np.dot(Scale,j)1,width=0.02,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.add_patch(Rectangle((,),1,1,fill=False,edgecolor=’g’,lw=2)) ax.add_patch(Rectangle((,),3,2,fill=False,edgecolor=’b’,lw=2)) plt.show() |
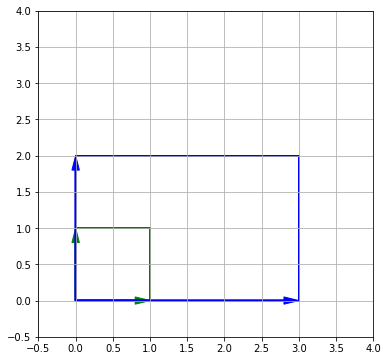
Определитель (determinant) матрицы показывает, какой будет площадь после трансформации.
| 1 | np.linalg.det(Scale) |
| 1 | 6.0 |
Так как мы сказали, что мы изменяем не только базисные, но и все остальные векторы пространства, определитель, по сути, показывает насколько сжимается или расширяется векторное пространство при трансформации.
Посмотрим на сдвиг.
|
1 |
Shear=np.array(1,1, ,1) ax=plt.axes() plt.xlim(-0.5,2.5) plt.ylim(-0.5,1.5) plt.grid() ax.arrow(,,i,i1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,j,j1,width=0.03,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’g’,ec=’g’) ax.arrow(,,np.dot(Shear,i),np.dot(Shear,i)1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.arrow(,,np.dot(Shear,j),np.dot(Shear,j)1,width=0.01,head_width=0.1,head_length=0.2,length_includes_head=True,fc=’b’,ec=’b’) ax.add_patch(Rectangle((,),1,1,fill=False,edgecolor=’g’,lw=2)) ax.add_patch(Polygon(,,1,,2,1,1,1,fill=False,edgecolor=’b’,lw=2)) plt.show() |
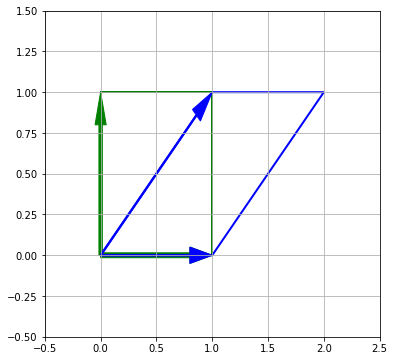
Напомню, что площадь параллелограмма можно найти, умножив основание на высоту.
| 1 | 1*1,np.linalg.det(Shear) |
| 1 | (1, 1.0) |
Метод Гаусса
Способ Гаусса используется для решения системы уравнений. На их базе составляется массив. Первые столбцы образуют из коэффициентов, стоящих после неизвестных, а последний из значений, расположенных после знака равно. Для нахождения определителя этим способом необходимо выполнить два шага:
- Привести матрицу к верхнетреугольной или нижнетреугольной форме путём элементарных преобразований.
- Сосчитать произведение всех элементов, расположенных на главной диагонали треугольного массива, заменив при этом полученный знак определителя на противоположный.
Например, необходимо найти детерминант системы уравнений:
n1 + 2 * n2 – 3 * n3 = — 4.
2*n1 + 5 * n2 – 4 * n3 = 0.
-3*n1 + n2 – 3 * n3 = 5.
На первом этапе составляют матрицу и решают её. Выделяют первую строку и пытаются обнулить все первые коэффициенты. Для этого каждый элемент нужно умножить на такое число, чтобы последующий элемент обнулился. Затем берут другую строку и обнуляют уже вторые элементы. Так, для заданной системы уравнений первую строку необходимо умножить на -2, а затем сложить со второй строкой. То есть первый элемент в первом столбце будет равен: x11 = -2 * 1 + 2 = 0; второй: x22 = -2 * 2 +5 = 1; третий: x33 = -2*(-3) – 4 = 2; четвёртый: x44 = -2* (-4) + 0 = 8.
Аналогичные действия проводят по отношению к элементам третьей строки. Для обнуления первую строчку умножают уже не на -2, а на тройку. В результате первый столбец будет состоять из двух нулевых элементов. Затем переходят к обнулению элементов во втором столбце. Делают это последовательным умножением третьей строки на – 7. В итоге получится массив с тремя нулевыми членами.
Опираясь на полученную матрицу, составляют новую систему уравнений:
n1 + 2 * n2 – 3 * n3 = -4.
n2 – 2 * n3 = 8.
–20 * n3 = -63.
Затем из последнего равенства находят n3. Полученное значение подставляют во второе уравнение и определяют n2. На последнем этапе, используя найденные величины, вычисляют n1. Для нахождения детерминанта определяют тип матрицы, в этом случае она нижнетреугольная, и вычисляют его значение det = (1 * 1 * (-20)) = -20.
Кроме быстрого определения ответа, они также показывают подробное решение поставленной задачи. Если же доступа к интернету нет, то можно выполнить расчёт и в excel. Делается это с помощью функции «=МОПРЕД».
Размерность пространства
В линейной алгебре размерность пространства определяется как количество линейно независимых векторов, образующих базис данного пространства. Она является одним из важных понятий, связанных с линейным пространством.
Размерность пространства может быть конечной или бесконечной. Конечное пространство имеет конечное число линейно независимых векторов в базисе, в то время как бесконечное пространство имеет бесконечное число таких векторов.
Размерность пространства установлена на основе того, сколько элементов необходимо указать для задания любого вектора в данном пространстве. Например, в трехмерном пространстве для задания любого вектора требуется указать его координаты по осям x, y и z. Таким образом, размерность трехмерного пространства равна трем.
Для пространства, заданного матрицей, размерность будет равна числу столбцов этой матрицы. Например, если задана матрица размером 3×2, то размерность пространства, образованного этой матрицей, будет равна 2.
Понимание размерности пространства играет важную роль в решении широкого спектра задач в области алгебры и геометрии, а также в приложениях в физике, экономике, компьютерной графике и других областях, связанных с моделированием и анализом данных.
Формула полного разложения детерминанта.
Здесь мы получим формулу полного разложения детерминанта порядка n, представляющую его как многочлен от элементов матрицы.
Введем предварительно некоторые определения. Мы будем называть перестановкой чисел 1,…, n эти числа, написанные в каком-либо определенном порядке. Например, из чисел 1 и 2 образуются две перестановки: 1, 2 и 2, 1. Перестановку чисел 1,…, n обозначим i_{1},…, i_{n}.
Число i_{k} виновно в нарушении порядка в перестановке i_{1},…, i_{n}, если оно стоит левее меньшего числа: k < s, но i_{k} > i_{s} Например, при n-4 в перестановке 2, 4, 3, 1 числа 2 и 3 виновны каждое в одном нарушении порядка, а число 4 — в двух. Итак, общее число нарушений порядка в перестановке равно четырем. Число всех нарушений порядка в перестановке i_{1},…, i_{n} мы обозначим N(i_{1},…, i_{n}).
Перестановка называется четной, если N(i_{1},…, i_{n}) — четное число, и нечетной в противном случае.
Теорема.
Формула полного разложения детерминанта: \tag{10} \mathbf{det}\,\begin{Vmatrix}a_{11}&…& a_{1n}\\\cdots\\a_{n1}&…& a_{nn}\end{Vmatrix}=\sum_{(i_{1},…, i_{n})} (-1)^{N(i_{1},…, i_{n})} a_{1i_{1}}a_{2i_{2}}…a_{ni_{n}}.
Сумма в правой части равенства берется по перестановкам. Это означает, что каждой перестановке чисел 1,…, n соответствует слагаемое. Слагаемое для перестановки i_{1},…, i_{n}, составляют так: берут из 1-й строки i_{1}-й элемент, из 2-й строки — i_{2}-й элемент и т. д. и перемножают их. В результате в произведение входит по одному и только по одному элементу из каждой строки и каждого столбца. Произведения складываются со знаками, определяемыми четностями соответствующих перестановок.
Формулу мы докажем по индукции. Пусть при n-2 дана матрица \begin{Vmatrix}a_{11}&…& a_{12}\\a_{21}&…& a_{22}\end{Vmatrix}.
Двум перестановкам 1, 2 и 2, 1 отвечают, соответственно, слагаемые (-1)^{N(1, 2)}a_{11}a_{22} и (-1)^{N(2, 1)}a_{12}a_{21} Их сумма равна a_{11}a_{22}-a_{12}a_{21} то есть как раз детерминанту данной матрицы.
Допустим, что формула верна для матриц порядка n-1, и докажем ее для произвольной матрицы A порядка n. Напишем разложение \mathbf{det}\,A по первой строке: \tag{11} \mathbf{det}\,A=\sum_{k=1}^{n}(-1)^{k+1}a_{1k}d_{1k}.
В k-е слагаемое этого разложения входит множитель d_{1k}, равный детерминанту подматрицы D_{1k}. Порядок этой матрицы n-1, и по предположению индукции d_{1k}=\mathbf{det}\,D_{1k}=\sum_{i_{1},…, i_{n-1}} (-1)^{N(i_{1},…, i_{n-1})}a_{2i_{1}}a_{3i_{2}}…a_{ni_{n-1}}.
Здесь все номера i_{1},…, i_{n} отличны от k, а первые индексы у сомножителей равны 2,…, n, так как, сохраняя старые обозначения для элементов матрицы A, мы должны учесть, что в D_{1k} не входят первая строка и k-й столбец.
Теперь в k-м слагаемом формулы можно внести множитель (-1)^{k+1}a_{1k} под знак суммы и записать это слагаемое так: (-1)^{k+1}a_{1k}d_{1k}=\sum_{i_{1},…, i_{n-1}} (-1)^{N(i_{1},…, i_{n-1})+k+1}a_{1k}a_{2i_{1}}a_{3i_{2}}…a_{ni_{n-1}}.
![Определитель [сайт патологического холостяка]](https://vsenazapad.ru/wp-content/uploads/9/b/0/9b0df762e37ffd1ad6bc7414f851840c.jpeg)
Числа k, i_{1},…, i_{n-1} образуют перестановку чисел 1,…, n, причем N(k, i_{1},…, i_{n-1})=N(i_{1},…, i_{n-1})+k-1, так как правее k стоит ровно k-1 чисел, меньших k. Следовательно, N(k, i_{1},…, i_{n-1}) имеет ту же четность, что и N(k, i_{1},…, i_{n-1})+k+1, и мы имеем (-1)^{k+1}a_{1k}d_{1k}=\sum_{i_{1},…, i_{n-1}} (-1)^{N(k,i_{1},…, i_{n-1})}a_{1k}a_{2i_{1}}a_{3i_{2}}…a_{ni_{n-1}}.
В правой части этого выражения собраны все те члены из суммы , которые соответствуют перестановкам, имеющим к на первом месте. В сумму входят слагаемые для любого k, и потому сумма содержит все члены суммы и, конечно, не содержит никаких других членов. Этим формула полного разложения доказана.
Миноры матрицы
В дополнение к определителю квадратной матрицы для заданной матрицы другие величины могут быть определены с использованием определителей, связанных с алгебраическими свойствами указанной матрицы. В частности, для квадратной или прямоугольной матрицы так называемые второстепенные определители порядка r могут быть определены из определителя квадратных подматриц размера r x r исходной матрицы. Учитывая матрицу :
Любой минор ранга r определяется как:
Следует отметить, что обычно будет большое количество миноров порядка r , на самом деле количество миноров порядка r матрицы m x n определяется как:
Интересным свойством является то, что ранг совпадает с порядком наибольшего возможного ненулевого минора, являясь вычислением миноров одним из наиболее часто используемых средств для вычисления ранга матрицы или линейной карты.
Свойства определителя
Рассмотрим свойства определителя более формально.
Свойство 1. Единичная матрица оставляет пространство без изменений. Ее определитель равен единице.
$$ det(I) = I $$
Свойство 2. Перестановка любых двух строк меняет знак определителя. В случае матрицы перестановок $P$
$$ det(P) = \begin{cases} 1, \text{четное число перестановок} \\ -1, \text{нечетное число перестановок} \end{cases} $$
Это правило легко продемонстрировать на матрице $2 \times 2$ с помощью формулы $ad-bc$
$$ det \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = 1 $$
$$ det \begin{vmatrix} 0 & 1 \\ 1 & 0 \end{vmatrix} = -1 $$
Свойство 3 (а). Если умножить строку матрицы на $t$, то и определитель умножается на $t$. Это логично, умножение константы $t$ на строку (то есть на один и тот же компонент каждого вектор-столбца) увеличивает объем n-мерного параллелепипеда, задаваемый этими векторами, в $t$ раз.
$$ \begin{pmatrix} ta & tb \\ c & d \end{pmatrix} \rightarrow t \cdot det \begin{vmatrix} a & b \\ c & d \end{vmatrix} $$
Свойство 3 (b).
$$ det \begin{vmatrix} a+a’ & b+b’ \\ c & d \end{vmatrix} = det \begin{vmatrix} a & b \\ c & d \end{vmatrix} + det \begin{vmatrix} a’ & b’ \\ c & d \end{vmatrix} $$
Свойство 4. Если две строки матрицы идентичны, то отпределитель равен нулю.
С одной стороны, перестановка двух одинаковых строк не должна менять знак определителя. С другой, по свойству 2 при перестановке строк знак определителя меняется. Условие $det(A) = -det(A)$ выполняется только, если определитель равен нулю.
Свойство 5. Если строки $i$ и $j$ не равны, то вычитание строки $t \cdot i, t \in \mathbb R$ из строки $j$ не изменит определителя.
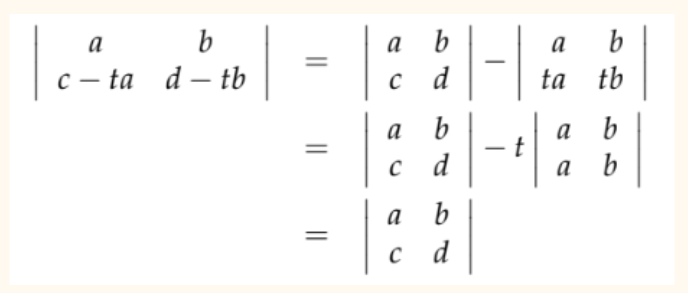
Свойство 6. Если есть строка, заполненная нулями, то определитель равен нулю. Следует из свойства 3(а).
Свойство 7. Определитель треугольной матрицы является произведением элементов главной диагонали (решающих элементов). Примеры⧉. Из этого свойства выводится формула определителя.
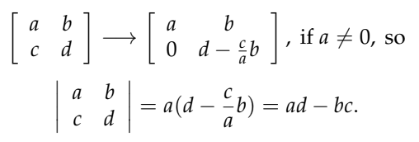
Примечание. Знак определителя при этом должен соответствовать четному или нечетному количеству перестановок строк, если последние имели место.
Свойство 8. Определитель равен нулю, когда матрица сингулярна. Следует из свойства 6.
Свойство 9. $det(AB) = (detA)(detB) $. Это логично, если считать, что определители $A$ и $B$ увеличивают пространство в $s$ и $t$ раз соотвественно, то вместе они увеличивают пространство в $st$ раз. Отсюда следует, что
$$ det (A^{-1}A) = 1 \rightarrow det(A^{-1}) = \frac{1}{det(A)} $$
$$ det (A^2) = (det (A))^2 $$
$$ det (2A) = 2^n (det (A)) $$
Последнее следует из свойства 3(а), примененного к каждой строке. Это также соответствует тому факту, что если вдвое увеличить длину, ширину и высоту, то объем вырастет в $2^3 = 8$ раз.
Свойство 10. $det (A^T) = det (A) $. На последующих занятиях мы узнаем, что матрицу $A$ можно разложить на компоненты $LU$, где $L$ — нижнетреугольная матрица с единицами на главной диагонали, а $U$ — верхне диагональная матрица. Тогда,
$$ det(A^T) = det(A) $$
$$ det(U^TL^T) = det(LU)$$
По свойствам 9 и 7,
$$ det(U^T) \cdot det(L^T) = det(L) \cdot det(U) $$
$$ det(L^T) = det(L) = 1 \rightarrow det(U^T)=det(U)$$
Так как $U$ — верхне треугольная матрица, то по свойству 7
$$ U^T = U $$
$$ det(U^T)=det(U) $$
$$ det(A^T) = det(A) $$
Как следствие, свойства, применимые к строкам матрицы, применяются и к столбцам.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю.
4.Свойства определителей. Определитель произведения матриц.
Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ.
Теорема Лапласа
Пример
Задание. Используя теорему Лапласа, вычислить определитель
Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Ответ.
Роль определителя матрицы в линейной алгебре
Одним из главных применений определителя матрицы является решение систем линейных уравнений. Определитель используется для определения условий совместности системы и нахождения ее решений. Если определитель матрицы системы равен нулю, то система несовместна, и решений не существует. В противном случае, система имеет единственное или бесконечное количество решений.
Определитель также связан с линейной независимостью векторов. Векторы являются линейно независимыми, если и только если определитель матрицы, составленной из этих векторов, не равен нулю. Если определитель равен нулю, то векторы линейно зависимы и могут быть выражены через линейные комбинации других векторов.
Кроме того, определитель матрицы используется при вычислении обратной матрицы. Матрица имеет обратную, если и только если ее определитель не равен нулю. Если определитель равен нулю, то матрица вырожденная и не имеет обратной.
Определитель матрицы также играет роль в вычислении собственных значений и векторов матрицы, определении различных характеристик матрицы, таких как ее ранг и след, и многое другое.
Таким образом, определитель матрицы представляет собой мощный инструмент в линейной алгебре, позволяющий анализировать и решать различные задачи, связанные с матрицами и системами линейных уравнений.
Определитель и решение систем линейных уравнений
Определитель матрицы играет важную роль в решении систем линейных уравнений. Система линейных уравнений представляет собой набор уравнений, где каждое уравнение содержит линейные комбинации переменных и констант. В такой системе необходимо найти значения переменных, которые удовлетворяют всем уравнениям одновременно.
Определитель матрицы помогает определить, имеет ли система уравнений единственное решение или же она не имеет решений вовсе. Если определитель матрицы системы равен нулю, то система имеет бесконечное количество решений. Если определитель не равен нулю, то система имеет единственное решение.
Для решения системы линейных уравнений с помощью определителя матрицы необходимо построить так называемую расширенную матрицу системы, в которой на месте правых частей уравнений будут стоять свободные члены. Затем требуется вычислить определитель этой расширенной матрицы. Если он не равен нулю, то система имеет единственное решение. В этом случае, используя формулу Крамера, можно найти значения переменных.
Определитель матрицы системы также позволяет определить линейную зависимость или независимость векторов системы. Если определитель матрицы равен нулю, то векторы системы линейно зависимы, что означает, что один из векторов может быть выражен как линейная комбинация других векторов. Если определитель не равен нулю, то векторы системы линейно независимы и образуют базисный набор, то есть каждый вектор нельзя выразить как линейную комбинацию других векторов.
Определитель и линейная независимость векторов
Для начала, давайте вспомним, что такое векторы и что значит быть линейно независимыми. Векторы — это объекты, которые могут быть представлены в виде списка чисел, обычно упорядоченных в столбец. Линейная независимость векторов означает, что ни один из векторов не может быть выражен в виде линейной комбинации других векторов.
Определитель матрицы может быть использован для проверки линейной независимости векторов. Для этого необходимо создать матрицу, в которой каждый вектор представлен в виде столбца. Затем вычислить определитель этой матрицы.
Если определитель равен нулю, это означает, что векторы линейно зависимы. В этом случае, хотя каждый вектор по отдельности может иметь ненулевую длину, один из векторов может быть выражен в виде линейной комбинации других векторов. То есть, существует нетривиальное решение системы уравнений, где все коэффициенты не равны нулю.
Если же определитель не равен нулю, это означает, что векторы линейно независимы. В этом случае, ни один из векторов не может быть выражен в виде линейной комбинации других векторов. То есть, существует только тривиальное решение системы уравнений, где все коэффициенты равны нулю.
Таким образом, определитель матрицы играет важную роль в определении линейной независимости векторов. Он позволяет нам понять, существует ли нетривиальное решение системы уравнений, где векторы выступают в качестве неизвестных. Благодаря этому свойству, определитель широко используется в различных областях, связанных с линейной алгеброй и векторным анализом.
| Вектор 1 | Вектор 2 | Вектор 3 |
|---|---|---|
| a1 | b1 | c1 |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
Несуществование решений линейных систем уравнений
Если определитель матрицы системы равен нулю, то говорят, что система является вырожденной. Вырожденная система не имеет решений или имеет бесконечное множество решений. Это зависит от конкретной системы и условий задачи.
Причины несуществования решений линейных систем могут быть различными:
- Уравнения могут быть противоречивыми (несовместными) — они не могут одновременно удовлетворять всем условиям системы.
- Уравнения могут быть линейно зависимыми — одно или несколько уравнений можно выразить через другие уравнения системы, что приводит к множеству решений.
- Уравнения могут содержать противоречивые уравнения (расходиться по значениям) или совпадающие уравнения (одинаковые) — это также приводит к несуществованию решений.
Если система уравнений является вырожденной, то она может свидетельствовать о наличии свойств и ограничений в рассматриваемой системе. Вырожденные системы могут возникать, например, в задачах линейного программирования или в случае сингулярной матрицы, и изучение их свойств является важным аспектом в различных областях математики и физики.
4.Определители. Свойства определителей.
Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:
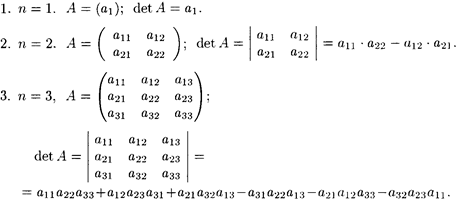
Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.
Вычисление определителя 2-го порядка иллюстрируется схемой:
Пример 4.1. Найти определители матриц
Решение:
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:
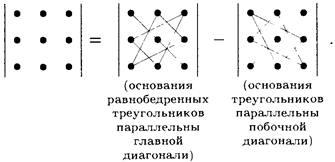
Пример 4.2. Вычислить определитель матрицы
Решение:
det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,
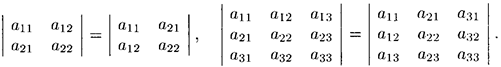
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,
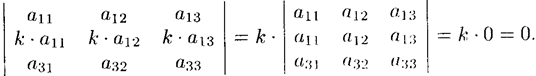
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,
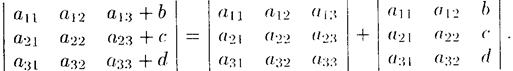
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.
Пример 4.3. Доказать, что
Решение: Действительно, используя свойства 5, 4 и 3 подучим
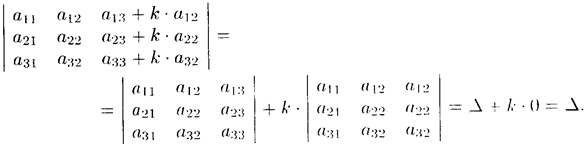
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента аij определителя n-го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij
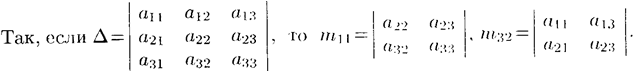
Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :
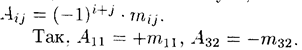
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что
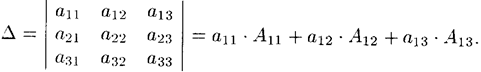
В самом деле, имеем
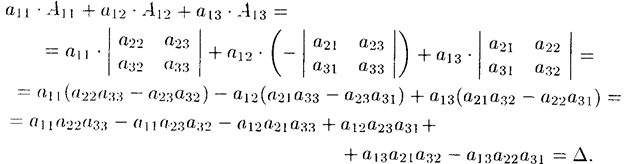
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Пример 4.4. Вычислите определитель матрицы
Решение: Для разложения определителя обычно выбирают гот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.
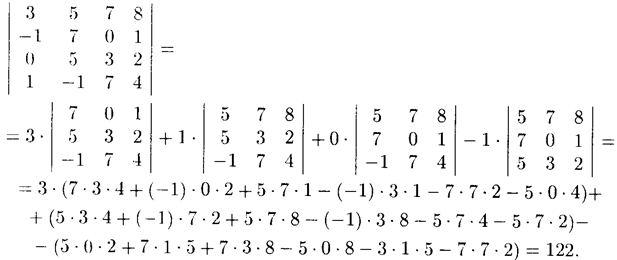
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,
Posted in Высшая математика, Лекции 1 курс and tagged Высшая математика
Нахождение значения
Для того чтобы понять, как находить детерминант матрицы, следует понять способы решения простых матриц 2х2 и 3х3. Умея находить их параметр, несложно будет определить детерминант и массив более высокого порядка. В математике матрицу принято записывать в круглых скобках, а определитель в прямых. Обозначают детерминант в формулах как det.
Если дана матрица второго порядка, то есть 2х2, то её определитель ищут по формуле: det = ab – dc, где: а и d – элементы первой строки, b и c – члены второй строки. То есть определитель находят как разность произведений диагональных элементов между собой. Например, пусть задана матрица:
| 13 9 |
| 1 11 |
Её параметр будет равняться: det = 13 * 11 – 9 * 1 = 143 – 9 = 134.
Пусть дана некая матрица три на три:
(1 2 1)
(5 -1 -1)
(-2 2 5)
Необходимо найти её определитель. Для массива 3х3 детерминант можно найти двумя способами:
- правилом Саррюса (треугольника);
- универсальным методом.
Схематично первый способ можно представить следующим образом:
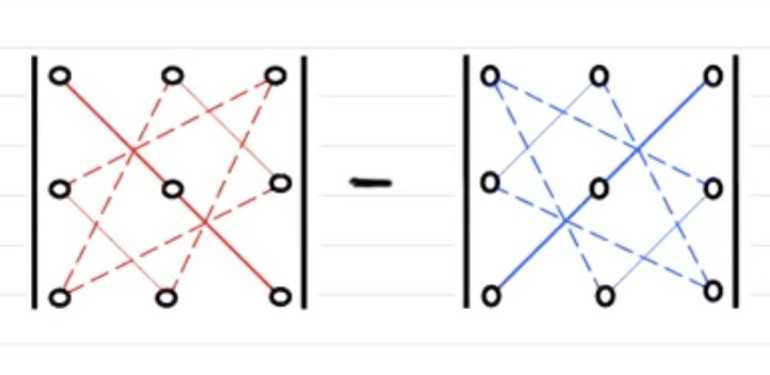
Для нахождения детерминанта по правилу треугольника нужно перемножить элементы массива, соединённые красными линиями, а затем их сложить. То же самое необходимо сделать с элементами, через которые проходит синяя линия. Затем из первого полученного значения вычесть второе. Вычитаемое и уменьшаемое состоит из трёх слагаемых. Определяются они двумя треугольниками и сумой элементов, стоящих на главной диагонали (сплошная линия).
Определитель будет равным: det = (1* (-1) * 5) + (5 * 2 * 1) + (2 * (-1) * (-2)) – (-2 * (-1) * (-1)) – (2 * 5 * 5) – (1 * 2 * (-1)) = — 5 + 10 + 4 – 2 – 20 + 2 = -11.
Второй способ проще. В его основе лежит метод разложения дискриминанта по первой строке или столбцу. То есть определитель можно найти по следующей формуле: det = a * n1 + b * n2 + c * n3, где: n1 — матрица 2х2, образованная с верхней левой части массива; n2 – матрица, полученная из второго и третьего члена первого столбца и третьего; n3 – массив, образованный из второго и третьего элемента первого столбца и третьего; a, b, c – элементы первой строчки.
Что такое Детерминант простыми словами
Размер матрицы определяется количеством строк m и столбцов n. Номера строк и столбцов — буквами i и j соответственно. Еще у матрицы есть не только строки и столбцы, но и диагонали. А теперь, что еще нужно в первую очередь знать о работе с матрицами. Как складывать матрицы Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать или вычитать матрицы просто — достаточно только сложить их соответствующие элементы. Приведем пример.
Вычитание выполняется по аналогии, только вместо плюса пишем минус. Как умножать матрицы Во-первых, запомните: матрицу А можно умножить на матрицу B, только если если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м. Вместо букв в матрице могут стоять реальные числа.
В языкознании детерминанты — это члены предложения , которые служат для распространения и не связаны с другими его членами. Определения в роли детерминанта не используются. Существительные и местоимения часто употребляются с предлогами. Детерминанты свободно присоединяются к разным предложениям и формируют его смысловую структуру, нередко являясь её обязательным компонентом. В одном предложении — особенно в разговорной речи — может встречаться несколько подобных словоформ «Для тебя у людей одни только отговорки».
Детерминант был впервые открыт лингвистом Н. Шведовой — соавтором известного русского толкового словаря.
Стоит сказать, что в быту термин используется редко так как того не требует сама специфика русской речи
Употреблять в быту непривычную терминологию стоит, осторожно, ведь можно остаться просто непонятым. Детерминантные и индетерминантные сорта и гибриды растений Эти термины стали популярны в силу их применения в сфере сада и огорода
Детерминантными и индетерминантными могут быть сорта томатов или огурцов. Рост детерминантных помидоров заранее определен.
К примеру, штамбовые томаты — самые ранние. Их рост ограничен появлением 4-8 кисточек. Рассаду можно высаживать после 40-45 суток, а плоды вы увидите примерно спустя 70-90 дней. Первая кисточка вырастает после появления 5-7 листочков. Индетерминантные помидоры отличаются ничем не ограниченным ростом. Растение будет развиваться до тех пор, пока будет жить. Разновидностей таких сортов не много.
Например, определитель разложенный по первому столбцу, имеет вид а его разложение по второй строке, имеет вид Вычислив каждый минор и умножив его на коэффициент, нетрудно убедиться в том, что оба выражения совпадают. Значение определителя. Такая сумма насчитывает ровно n! Каждый член суммы содержит по одному члену из каждого столбца и каждой строки определителя. Можно доказать, что эта сумма совпадает с выражением, получаемым при разложении определителя по минорам. Свойства определителя. Среди наиболее важных свойств определителя назовем следующие. Например, iv Значение определителя не изменится, если к элементам одной строки или столбца прибавить соответствующие элементы другой строки или столбца , умноженные на произвольный множитель. В следующем примере элементы второй строки умножаются на —2 и прибавляются к элементам первой строки: v Если поменять местами две строки или два столбца , то определитель изменит знак: vi Если все элементы одной строки или одного столбца содержат общий множитель, то этот множитель можно вынести за знак определителя: Пример.
Вычислим значение следующего определителя 4-го порядка: Прибавим к 1-й строке 4-ю строку: Вычтем 1-й столбец из 4-го столбца: Умножим 3-й столбец на 3 и вычтем из 4-го столбца: Если угодно, то строки и столбцы можно поменять местами: Разложим определитель по элементам четвертой строки.