Способы нахождения средней скорости в физике

Средняя скорость

Как можно сравнивать скорости неравномерных движений?

Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.

Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.

В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени

Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта

Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.

Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается

Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.

$$v_{ср}={Delta x_{общ} over Delta t_{общ}}$$

Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.

Рис. 3. Средняя скорость.

Что мы узнали?

Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

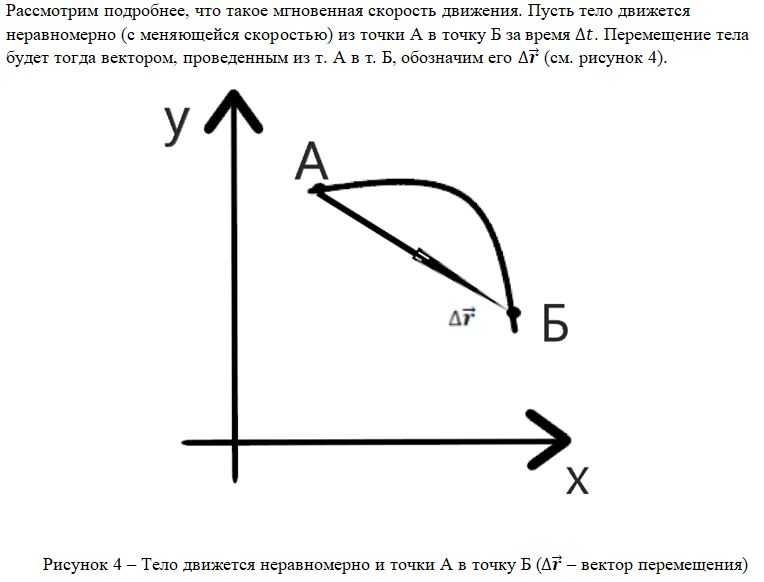
Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n,  и найти средние скорости за эти отрезки времени:

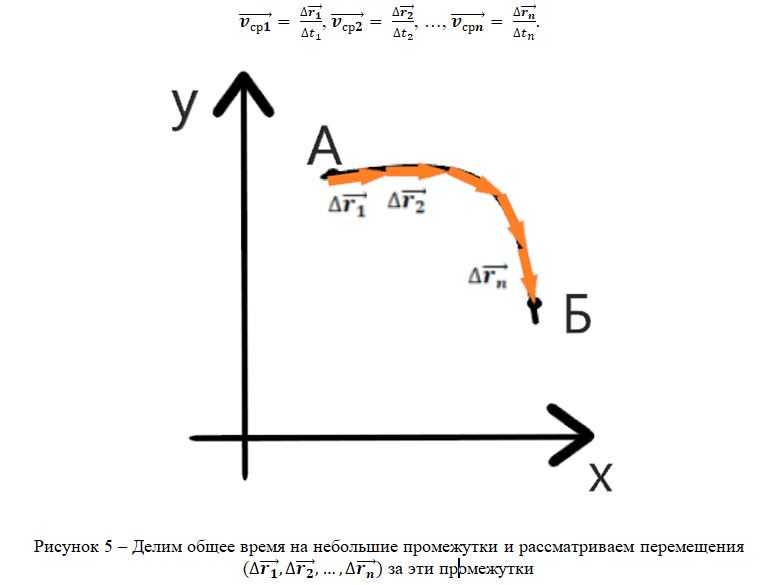
А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

О неравномерности вращения Земли вокруг своей оси

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52 с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на Солнечные таблицы (англ.) русск. Саймона Ньюкомба (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях.

Задачи

Задача №1

Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 \frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.

Переведем единицы измерения скорость в СИ и решим задачу.

$120 \frac{км}{ч} = 120 \cdot \frac{1000 \space м}{3600 \space с} \approx 33 \frac{м}{с}$.

Дано:$\upsilon = 120 \frac{км}{ч}$$t = 3 \space c$

СИ:$\upsilon = 33 \frac{м}{с}$

$S — ?$

Показать решение и ответ

Скрыть

Решение:

Гепард двигается равномерно в течение 3 с.Путь, который он проходит за это время:$S = \upsilon t$,$S = 33 \frac{м}{с} \cdot 3 с \approx 100 \space м$

Ответ: $S = 100 \space м$.

Задача №2

Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 \frac{км}{ч}$. Сколько времени у них занимает такой полет?

Переведем единицы измерения скорость в СИ и решим задачу.

$40 \frac{км}{ч} = 40 \cdot \frac{1000 м}{3600 с} \approx 11 \frac{м}{с}$,$900 \space км = 900 \space 000 м$.

Дано:$\upsilon_{ср} = 40 \frac{км}{ч}$$S = 900 \space км$

CИ:$\upsilon_{ср} = 11 \frac{м}{с}$$S = 900 \space 000 \space м$

$t-?$

Показать решение и ответ

Скрыть

Решение:

Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:$t = \frac{s}{\upsilon_{ср}}$,$t = \frac{900 \space 000 \space м}{11 \frac{м}{с}} \approx 82 \space 000 \space с$.

Переведем время в часы:$1 \space ч = 60 \space мин = 60 \cdot 60 \space c = 3600 \space c$.

Тогда:$t = \frac{82 \space 000 \space c}{3600 \space c} \approx 23 \space ч$.

Ответ: $t = 23 \space ч$.

Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить  на маленькие отрезки времени и рассматривать ускорение на каждом из них.

Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Для чего это нужно?

Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.

Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.

Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.

Равнопеременное движение

Равнопеременное движение – это движение, при котором за любые равные промежутки времени происходит одинаковое изменение скорости. При равнопеременном движении значение и направление ускорения не меняются:

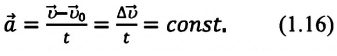
При равнопеременном движении проекция ускорения на любую ось, например ось

Это значит, что при равнопеременном движении график зависимости ускорения от времени представляет собой прямую линию, параллельную оси времени, – проекция ускорения на выбранную ось от времени не зависит (с).

В СИ за единицу ускорения принят – ускорение такого равнопеременного движения, при котором материальная точка за 1 секунду изменяет свою скорость на

Знаете ли вы? Ускорение—одна из наиболее значимых величин, используемых в физике и технике. Известно, что при постепенном торможении автомобиля, автобуса и поезда пассажиры не чувствуют дискомфорта, однако при резком торможении для них возникает серьезная опасность

Значит, важно не просто изменение скорости, а быстрота изменения скорости. Для контроля за изменением скорости машин и механизмов используется прибор, измеряющий ускорение — акселерометр (лат.: accelero — “ускоряю ” и греч.: metreo – “измеряю “) (d)

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Прямолинейное равноускоренное движение
• Сложение скоростей
• Ускорение в физике
• Скорость при равнопеременном движении
• Скалярные и векторные величины и действия над ними
• Проекция вектора на ось
• Путь и перемещение
• Равномерное прямолинейное движение

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

http://reshator.com/sprav/fizika/7-klass/neravnomernoe-pryamolinejnoe-dvizhenie-srednyaya-skorost/

http://www.evkova.org/pryamolinejnoe-neravnomernoe-dvizhenie-v-fizike

Неравномерное прямолинейное движение. Средняя скорость

п.1. График скорости при неравномерном прямолинейном движении

Прямолинейное и равномерное движение возможно лишь на участке пути.Любое тело со временем меняет свою скорость, как по величине, так и по направлению.

Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.

п.2. Как найти путь и перемещение по графику скорости?

Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком \(\triangle t\) на оси \(t\) (см. §8 данного справочника).

п.3. Средняя скорость и средняя путевая скорость

В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: \begin |\overrightarrow>|=\frac|>=\frac=\frac 61=6\ \text\\ v_=\frac st=\frac 61=6\ \text \end Величина средней скорости равна средней путевой скорости.

А вот для случая, когда велосипедист развернулся и пошел обратно: \begin |\overrightarrow>|=\frac|>=\frac=\frac 31=3\ \text\\ v_=\frac st=\frac 61=6\ \text \end Величина средней скорости меньше средней путевой скорости.

п.4. Задачи

Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.

Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	40	\(\frac=\frac\)	\(2d\)
2й участок	80	\(\frac\)	\(d\)
Сумма	—	\(t=\frac+\frac\)	\(s=2d+d=3d\)

Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	90	\(\frac=\frac\)	\(\frac s2\)
2й участок	30	\(\frac=\frac\)	\(\frac s2\)
Сумма	—	\(t=\frac+\frac\)	\(s\)

Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	\(\frac\)	\(4t\)	\(d\)
2й участок	\(\frac\)	\(t\)	\(4d\)
3й участок	\(\frac\)	\(20t\)	\(45d\)
Сумма	—	\(25t\)	\(50d\)

Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?

Скорость, км/ч	Время, ч	Расстояние, км
1й участок	\(10v\)	\(\frac=\frac\)	\(\frac s2\)
2й участок	\(\frac\)	\(\frac=\frac sv\)	\(\frac s2\)
Сумма	—	\(t=\frac+\frac sv\)	\(s\)

п.5. Лабораторная работа №3. Определение средней скорости движения тела

Цель работыНаучиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.

Теоретические сведенияВ лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.

Длина участков измеряется с помощью мерной ленты с ценой деления \(\triangle=1\) см,инструментальная погрешность равна: \(d=\frac=0,5\) смАбсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: \(\triangle s_1=\triangle s_2=d=0,5\) смПогрешность суммы двух длин: \(\triangle(s_1+s_2)= \triangle s_1+\triangle s_2=2d=1\) см

Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).Погрешность суммы двух измерений: \(\triangle(t_1+t_2)=\triangle t_1+\triangle t_2\)

Приборы и материалыДва желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.

Ход работы1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.

Движение свободно падающего тела

Под свободным падением понимается движение тела под действием одной только силы тяжести. При решении многих задач сопротивлением воздуха пренебрегают и считают тело свободно падающим. Находясь в поле тяготения Земли (или другой планеты), все свободно падающие тела двигаются с одинаковым ускорением, которое называется ускорением свободного падения. Это ускорение направлено к центру планеты.

Земное ускорение свободного падения обозначается как g. На небольших высотах считается, что g = 9,8 м/с2. Для решения многих задач это значение округляется до десяти и принимается g = 10 м/с2.

Примеры типичных заданий на среднюю скорость в ЕГЭ

Задание 1: Автобус выезжает из города А в город Б со скоростью 60 км/ч. Через 1 ч после выезда автобуса с той же скоростью, но в противоположном направлении выезжает из города Б автомобиль. Когда автомобиль встретит автобус?

Задание 2: Самолет вылетел из города А в город Б со скоростью 500 км/ч, расстояние между городами составляет 4000 км. Через сколько часов самолет прибудет в город Б?

Задание 3: Лодка движется вверх по течению реки со скоростью 20 км/ч, против течения реки со скоростью 12 км/ч. С какой скоростью течет река, если скорость лодки в неподвижной воде 16 км/ч?

Задание 4: Велосипедист едет по прямой дороге со скоростью 30 км/ч, через 2 ч после его старта в том же направлении выезжает автомобиль со скоростью 80 км/ч. Через какое время автомобиль догонит велосипедиста?

Задание 5: Мотоциклист проехал первую половину пути со скоростью 60 км/ч, вторую половину пути – со скоростью 80 км/ч. Какова средняя скорость мотоциклиста на всем пути?

Задание 6: На одном участке трассы автомобиль ехал со скоростью 90 км/ч, на следующем – со скоростью 60 км/ч. Какова была средняя скорость автомобиля на всем пути?

Задание 7: Человек идет встречным шагом со скоростью 6 км/ч. Грузовик, идущий той же дорогой, в сомнительной обстановке едет со скоростью 30 км/ч и, не заметив человека перед собой, начинает тормозить, замедляясь равномерно. Как долго это происходит, если расстояние между ними было изначально 150 м?

Задание 8: Поезд выезжает из города А в город Б со скоростью 80 км/ч. Через 1 ч после выезда из города А встречный поезд выезжает из города Б в город А со скоростью 100 км/ч. Когда встретятся поезда, если расстояние между городами 400 км?

Задание 9: Лодка движется под углом 30° к направлению течения реки со скоростью 15 км/ч, скорость течения реки 10 км/ч. Найти скорость лодки относительно берега.

Задание 10: Автомобиль едет по кольцевой дороге. Его скорость на первой половине пути 80 км/ч, на второй 60 км/ч. Найти среднюю скорость автомобиля на всем пути.

Виды скоростей

Скорость является векторной величиной. Скорость характеризует направление движения и его быстроту. Скорость измеряется в метрах, пройденных в секунду: м/с. В кинематике также используются такие понятия, как средняя скорость и средняя путевая скорость.

Средняя скорость — это отношение перемещения во времени, за которое это перемещение было совершено. Величина векторная. Рассчитывается по формуле:

Средняя путевая скорость — это отношение пройденного пути (не перемещения) ко времени, в течение которого этот путь был пройден. Величина скалярная. Рассчитывается по формуле:

V_ср = L / t

Мгновенная скорость — это скорость, которую тело имеет в конкретный момент времени. Величина векторная. Формулы расчета зависят от вида движения. Вектор мгновенной скорости направлен по касательной к траектории.

Примеры решения задач

Задача 1

Такси в течение рабочего дня совершило несколько поездок. По первому вызову оно проехало 150 км, затратив на это 2 часа. Следующий пассажир заказал поездку на расстояние 250 км, которое проехал за 3 часа. Третий заказал поездку в сельскую местность с труднопроходимыми дорогами в 90 км, которую совершил за 2 часа. Какой была средняя скорость такси в течение описанного рабочего дня?

Решение.

Обозначим в первой поездке путь в 150 км буквой S₁, а время (2ч) —  t₁.

Вторая поездка: S₂ = 250, а время (3ч) —  t₂.

Третья поездка в течение дня: S₃ = 90км, а время (2ч) —  t₃.

S= S₁+ S₂+ S₃

t= t₁+ t₂+ t₃

V_ср= S/ t=( S₁+ S₂+ S₃)/(t₁+ t₂+ t₃)= (150+250+90)/(2+3+2)=490/7=70км/ч

Ответ: средняя скорость такси в течение рабочего дня была равна 70 км/ч.

Задача 2

Автомобиль проехал путь 300км. На первом отрезке пути (120 км) его скорость была равна 60 км/ч, на втором (80 км) – 80 км/ч, на третьем (180 км) – 90 км/ч. Какой была средняя скорость на протяжении всей дороги?

Зная, что в целом пройден путь 300 км, для определения средней скорости необходимо знать, сколько времени на него ушло.

Это можно определить из формул:

t₁=S₁/ V₁ =120/60=2ч

t₂=S₂/ V₂ =80/80=1ч

t₃=S₃/ V₃ =180/90=2ч

t=t₁+t₂+t₃=2+1+2=5ч

Теперь можно найти среднюю скорость по формуле: V _ср=S/ t=300/5=60 км/ч

Ответ: средняя скорость движения автомобиля на всем протяжении пути равна 60 км/ч.

Задача 3

Два велосипедиста едут дистанцию 100 км. Известно, что у первого средняя скорость движения на 3 км/ч больше, чем у второго. Второй велосипедист разбил свой путь на два отрезка. Первые 45 км он проехал за 1 час, следующие 55 км — за 3 часа.  Каковы средние скорости обоих велосипедистов?

Решение.

Первым действием найдем среднюю скорость второго велосипедиста. Для этого высчитаем время, которое ушло на дорогу: 1час + 3 часа= 4 часа

Для нахождения его средней скорости разделим его путь (100 км) на время, затраченное на дорогу.

V_ср1 = S1/t1 = 100/4 = 25 км/ч

Из условия известно, что средняя скорость второго велосипедиста на 3 км/ч меньше, чем первого, а, следовательно:

V_ср2 = 25-3 = 22 км/ч

Ответ: средняя скорость первого велосипедиста равна 25 км/ч, второго — 22 км/ч.

Задача 4

Два автомобиля затратили на свои поездки по 5 часов. Длина пути первого составила 600 км. Известно, что его средняя скорость была выше средней скорости второго автомобиля на 8 км/ч. Какой путь прошел второй автомобиль?

Решение.

Первым действием найдем среднюю скорость второго автомобиля. Для этого 

V_ср2=V_ср1-8

Для применения данной формулы необходимо найти среднюю скорость первого автомобиля. Ее находим по формуле: V₁=600/5=120км/ч

V_ср2=120-8=112 км/ч

Теперь можно найти, какой длины путь был пройден вторым автомобилем. Для этого применяем формулу:

S₂=V₂*t₂=112*5=560 км

Алгоритм на все случаи жизни

Для того чтобы наверняка избежать ошибки, при решении вопроса, как найти среднюю скорость, достаточно запомнить и выполнить простую последовательность действий:

• определить весь путь, просуммировав длины отдельных его участков;
• установить всё время пути;
• поделить первый результат на второй, неизвестные, не заданные в задаче величины при этом (при условии корректной формулировки условий) сокращаются.

В статье рассмотрены простейшие случаи, когда исходные данные приводятся для равных долей времени или равных участков пути. В общем случае соотношение хронологических промежутков либо пройденных телом расстояний может быть самым произвольным (но при этом математически определённым, выраженным конкретным целым числом или дробью). Правило обращения к соотношению v ср = S: t
абсолютно универсально и никогда не подводит, сколь бы сложные на первый взгляд алгебраические преобразования ни приходилось выполнять.

Напоследок отметим: для наблюдательных читателей не осталась незамеченной практическая значимость использования верного алгоритма. Правильно рассчитанная средняя скорость в приведённых примерах оказалась несколько ниже «средней температуры» на трассе. Поэтому ложный алгоритм для систем, фиксирующих превышения скорости, означал бы большее число ошибочных постановлений ГИБДД, высылаемых в «письмах счастья» водителям.

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

V ср = S/t.

• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с2
2) 20 м/с2
3) 2 м/с2
4) 0,5 м/с2

3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​\( Оx \)​. У какого из тел в момент времени ​\( t_1 \)​ скорость движения равна нулю?

4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​\( Оx \)​.

Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

1) 1 м/с2
2) -1 м/с2
3) 2 м/с2
4) -2 м/с2

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?

1) 1
2) 2
3) 3
4) 4

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

11. Два тела движутся по оси ​\( Оx \)​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​\( t_3-t_5 \)​ тело 2 движется равноускоренно.
2) К моменту времени ​\( t_2 \)​ от начала движения тела прошли одинаковые пути.
3) В промежутке времени ​\( 0-t_3 \)​ тело 2 находится в покое.
4) В момент времени ​\( t_5 \)​ тело 1 останавливается.
5) В промежутке времени ​\( t_3-t_4 \)​ ускорение ​\( a_x \)​ тела 1 отрицательно.

12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ​\( t_1 \)​ тело имело максимальное по модулю ускорение.
4) Момент времени ​\( t_3 \)​ соответствует остановке тела.
5) В момент времени ​\( t_2 \)​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​\( x=12t-t^2 \)​. В какой момент времени скорость движения равна нулю?

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с2.

Важно! \( g \) = 9,8 м/с2, но при решении задач считается, что \( g \) = 10 м/с2

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

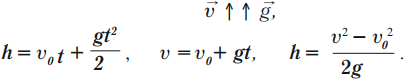
Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

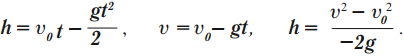
Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

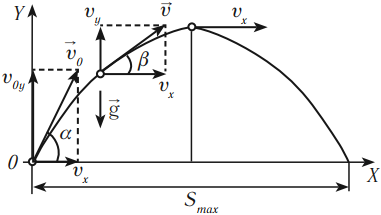
Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е

тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Упражнения

Упражнение №1

Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 \space с$.

Дано:$\upsilon_1 = 22 \frac{м}{с}$$\upsilon_2 = 20 \frac{м}{с}$$\upsilon_3 = 8000 \frac{м}{с}$$t = 5 \space с$

$S_1 — ?$$S_2 — ?$$S_3 — ?$

Показать решение и ответ

Скрыть

Решение:

Путь, пройденный страусом:$S_1 = \upsilon_1 t$,$S_1 = 22 \frac{м}{с} \cdot 5 \space с = 110 \space м$.

Путь, пройденный автомобилем:$S_2 = \upsilon_2 t$,$S_2 = 20 \frac{м}{с} \cdot 5 \space с = 100 \space м$.

Путь, пройденный искусственным спутником Земли:$S_3 = \upsilon_3 t$,$S_3 = 8000 \frac{м}{с} \cdot 5 \space с = 40 \space 000 \space м = 40 \space км$.

Ответ: $S_1 = 110 \space м$, $S_2 = 100 \space м$, $S_3 = 40 \space км$.

Упражнение №2

На велосипеде можно без особого напряжения ехать со скоростью $3 \frac{м}{с}$. На какое расстояние можно уехать за $1.5 \space ч$?

Дано:$t = 1.5 \space ч$$\upsilon = 3 \frac{м}{с}$

СИ:$t = 5400 \space с$

$S — ?$

Показать решение и ответ

Скрыть

Решение:

Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:$S = \upsilon t$,$S = 3 \frac{м}{с} \cdot 5400 \space с = 16 \space 200 \space м = 16.2 \space км$.

Ответ: $S = 16.2 \space км$.

Упражнение №3

На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 \space ч$. Затем рассчитайте скорость тела.

Рисунок 4. График зависимости пути от времени равномерного движения

Определим из графика путь, пройденный телом за $2 \space ч$. Этому времени на графике соответствует значение пути, равное $200 \space км$. Запишем условие задачи и решим ее.

Дано:$S = 200 \space км$$t = 2 \space ч$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

Скорость равномерного движения рассчитываем по формуле:$\upsilon = \frac{S}{t}$.

$\upsilon = \frac{200 \space км}{2 \space ч} = 100 \frac{км}{ч}$.

Ответ: $\upsilon = 100 \frac{км}{ч}$.

Упражнение №4

График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 \space ч$, $4 \space ч$.

Рисунок 5. График зависимости скорости равномерного движения от времени

Из графика видно, что скорость тела равна $8 \frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.

Дано:$t_1 = 2 \space ч$$t_2 = 4 \space ч$$\upsilon = 8 \frac{м}{с}$

СИ:$t_1 = 7200 \space с$$t_2 = 14 \space 400 \space с$

$S_1 — ?$$S_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Путь рассчитаем по формуле: $S = \upsilon t$.

За $2 \space ч$ тело пройдет путь:$S_1 = \upsilon t_1$,$S_1 = 8 \frac{м}{с} \cdot 7200 \space с = 57 \space 600 \space м = 57.6 \space км$.

За $4 \space ч$ тело пройдет путь:$S_2 = \upsilon t_2$,$S_2 = 8 \frac{м}{с} \cdot 14 \space 400 \space с = 115 \space 200 \space м = 115.2 \space км$.

Ответ: $S_1 = 57.6 \space км$, $S_2 = 115.2 \space км$.

Упражнения №5

По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?

Рисунок 6. Графики зависимости путей от времени равномерного движения двух тел

Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 \space м$, за $2 \space с$. Второе тело (II) проходит путь, равный $4 \space м$, за $4 \space с$. Запишем условие задачи и решим ее.

Дано:$S = 4 \space м$$t_1 = 2 \space с$$t_2 = 4 \space с$

$\upsilon_1 — ?$$\upsilon_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Рассчитаем скорость первого тела:$\upsilon_1 = \frac{S}{t_1}$,$\upsilon_1 = \frac{4 \space м}{2 \space с} = 2 \frac{м}{с}$.

Рассчитаем скорость второго тела:$\upsilon_2 = \frac{S}{t_2}$,$\upsilon_2 = \frac{4 \space м}{4 \space с} = 1 \frac{м}{с}$.

Получается, что скорость первого тела больше скорости второго.

Ответ: $\upsilon_1 = 2 \frac{м}{с}$, $\upsilon_2 = 1 \frac{м}{с}$, $\upsilon_1 > \upsilon_2$.