Окружность и круг

Геометрические параметры круга

Круг является одной из фундаментальных геометрических фигур, а его параметры и свойства играют важную роль в различных науках и областях знания.

• Радиус: радиусом круга называется отрезок, соединяющий центр круга с любой точкой его окружности. Обозначается буквой R.
• Диаметр: диаметром круга называется отрезок, соединяющий две точки на его окружности и проходящий через его центр. Диаметр в два раза больше радиуса и обозначается буквой D.
• Длина окружности: длиной окружности называется общая длина ее границы. Она вычисляется по формуле L = 2πR, где π (пи) – математическая константа, приближенно равная 3,14159.
• Площадь: площадью круга называется площадь фигуры, ограниченной его границей. Она вычисляется по формуле S = πR^2.

Круг имеет множество интересных и полезных свойств, которые используются в различных областях, например, в физике, геометрии, инженерии и технологии. Изучение геометрических параметров круга позволяет более глубоко понять его природу и использовать его свойства в практических задачах.

Примечание: в данной статье используется традиционная для России терминология, где площадь и длина окружности зависят от радиуса круга.

Практическое применение

Знак дуги в геометрии имеет широкое практическое применение и используется для решения различных задач. Приведем некоторые примеры:

Пример	Описание
Строительство	При планировании и проектировании зданий и сооружений, знаки дуг используются для определения радиуса поворота и кривизны дорожных и транспортных развязок. Это позволяет строителям создавать удобные и безопасные объекты.
Дизайн	В дизайне знаки дуг активно используются для создания эстетических и гармоничных композиций. Они могут служить в качестве органичных элементов декора, логотипов или части общего визуального стиля.
Картография	На картах и планах городов используются знаки дуг, чтобы указать направление движения или просто отобразить графически криволинейные объекты, такие как реки, дороги или границы территорий.
Статистика и анализ данных	В анализе данных знаки дуг используются для построения диаграмм и графиков, чтобы визуализировать процентные соотношения или относительные значения между различными категориями. Это помогает упростить представление сложных статистических данных.
Геодезия	В геодезии знаки дуг применяются для измерения расстояний и углов при проведении геодезических съемок и определении координат точек на местности. Они позволяют геодезистам проводить точные измерения и создавать карты и планы с высокой степенью точности.

Это лишь некоторые примеры практического применения знаков дуг в геометрии. В зависимости от конкретной области и задачи, данное геометрическое понятие может иметь и другие применения.

Круг

Окружность — это фигура, которая представляет собой замкнутую кривую линию, состоящую из всех точек, равноудаленных от данной точки, называемой центром окружности.

Форма круга является симметричной и имеет бесконечное количество осей симметрии.

Радиус круга представляет собой расстояние от мидпоинта окружности до ее центра.

Диаметр круга — это отрезок, который соединяет две противоположные точки на окружности, проходящий через ее центр.

Площадь круга — это количество площади, занимаемое кругом на плоскости. Она вычисляется по формуле: S = πr², где π — постоянное число, равное приблизительно 3.14159, r — радиус круга.

Круг является одной из основных фигур в геометрии и имеет множество применений в различных областях науки и практической деятельности.

Определение и свойства

У окружности есть несколько важных характеристик. Радиус — это расстояние от центра окружности до любой её точки. Окружность также имеет диаметр — это отрезок, соединяющий две противоположные точки на окружности, проходящие через её центр. Диаметр равен удвоенному значению радиуса.

Площадь круга — это количество плоскости, которое содержится внутри его границы. Она вычисляется по формуле:

S = π * r^2.

где S — площадь круга, π (пи) — математическая константа, примерное значение которой равно 3,14, r — радиус круга.

Формула круга

Для определения площади круга используется формула:

1. Найдите диаметр круга, который представляет собой отрезок, соединяющий две точки на окружности и проходящий через центр.
2. Разделите диаметр пополам, чтобы найти радиус, который является расстоянием от центра до любой точки на окружности.
3. Возведите радиус в квадрат.
4. Умножьте полученное значение на число Пи (π), которое приближенно равно 3,14159.
5. Полученное произведение и будет площадью круга.

Формула площади круга:

S = π * r2

Где:

• S — площадь круга;
• π (Пи) — математическая константа, приближенно равная 3,14159;
• r — радиус окружности.

Используя формулу площади круга, можно вычислить его территорию, то есть площадь, занимаемую кругом.

Примеры использования

Окружность — это геометрическая фигура, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от заданной точки. Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. По своей форме окружность представляет собой замкнутую кривую с одной границей.

Круг — это геометрическая фигура, образованная всеми точками плоскости, которые находятся на определенном расстоянии от заданной точки, и сама эта точка — центр круга. Также круг определяется его радиусом, который является расстоянием от центра до любой точки на окружности. Круг представляет собой фигуру, ограниченную окружностью. Территория, заключенная внутри круга, называется площадью круга.

Примеры использования окружности и круга можно найти во многих областях жизни. Например, в архитектуре использование окружностей и кругов позволяет создавать красивые и эстетически приятные формы зданий и сооружений. В инженерии они применяются для создания колес и шестерен, а также для моделирования движений и процессов. В географии и картографии окружности используются для построения меридианов и параллелей на географических картах.

Понимание различий и применение окружностей и кругов помогает визуализировать и анализировать различные формы и границы, а также решать различные задачи в области геометрии и других наук.

Как построить окружность по данным условиям?

Построение окружности может быть выполнено с помощью различных методов и инструментов. Рассмотрим наиболее распространенный способ построения окружности по заданным условиям.

1. Задайте условия окружности. Они могут быть представлены в виде радиуса (R) или координат центра окружности (x, y).
2. Определите центр окружности. Если известны координаты центра (x, y), отметьте эту точку на плоскости.
3. Постройте радиус окружности. Это отрезок, соединяющий центр окружности с любой точкой на его окружности. Используйте линейку или компас, чтобы провести отрезок нужной длины.
4. Пометьте на окружности несколько точек. Проведите линию через центр окружности и поставьте отметки на прямой или правой угол для удобства.
5. Используйте линейку или компас для соединения отметок на окружности. Проведите дуги или отрезки, соединяющие эти точки, чтобы получить окружность.

Таким образом, используя указанный метод, вы сможете построить окружность по заданным условиям и получить графическое представление этой фигуры.

Пример:

Пусть дана окружность с радиусом 5 единиц и центром в точке (3, 4).

1. Задаем условия окружности: R = 5 или (3, 4).
2. Определяем центр: центр окружности находится в точке (3, 4).
3. Строим радиус: используя компас или линейку, проводим отрезок длиной 5 единиц от центра окружности.
4. Помечаем несколько точек на окружности: для удобства выбираем несколько угловых точек окружности.
5. Соединяем отметки на окружности: с помощью компаса или линейки проводим дуги или отрезки, соединяющие эти точки. Полученная линия будет представлять окружность.

Теперь вы знаете, как построить окружность по данным условиям и можете использовать этот метод для решения различных задач и заданий.

Определение и основные понятия

Дуга в геометрии представляет собой часть окружности, которая ограничена двумя точками на этой окружности. Дуга состоит из всех точек, которые находятся на окружности и расположены между заданными конечными точками.

Окружность – это замкнутая кривая, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от данной точки, называемой центром окружности.

Дугу можно описать с помощью центрального угла. Центральный угол – это угол, вершина которого находится в центре окружности, а сторонки – это лучи, которые соединяют центр окружности с конечными точками дуги.

Дуга может быть полной или неполной. Полная дуга – это дуга, которая охватывает весь окружность и равняется 360 градусам или 2π радианам. Неполная дуга – это дуга, которая охватывает только часть окружности и имеет меньший центральный угол.

Каждая дуга имеет свою длину, которая измеряется в единицах длины. Длина дуги зависит от его центрального угла и радиуса окружности. Для нахождения длины дуги используется формула:

1. для измерения в градусах: L = (α/360) × 2πR, где L — длина дуги, α — центральный угол в градусах, R — радиус окружности.
2. для измерения в радианах: L = αR, где L — длина дуги, α — центральный угол в радианах, R — радиус окружности.

Дуги могут быть использованы для измерения углов, создания фигур и определения различных геометрических свойств в геометрии.

Углы и нахождение

Знание геометрических углов имеет важное значение для решения многих задач и нахождения различных значений. Рассмотрим наиболее распространенные способы определения углов

Способ нахождения	Описание
Измерение с помощью градусного треугольника	Углы могут быть измерены с помощью градусного треугольника. Для этого на противоположной стороне угла отмечается точка, а затем определяется значение угла с помощью шкалы на треугольнике.
Измерение с помощью универсального угломера	Углы также можно измерять с помощью специального инструмента — универсального угломера. Он позволяет определить значение угла с большей точностью и в различных плоскостях.
Использование геометрических формул	В некоторых случаях можно использовать геометрические формулы для нахождения значений углов в зависимости от заданных параметров фигур. Например, для нахождения углов треугольника можно воспользоваться формулой синусов или косинусов.

Умение определять и находить углы с помощью этих методов позволяет решать разнообразные геометрические задачи, а также имеет практическое применение в инженерных и архитектурных расчетах.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

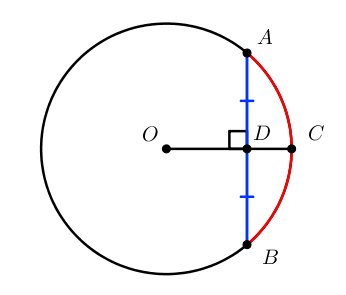
Теорема 1: Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

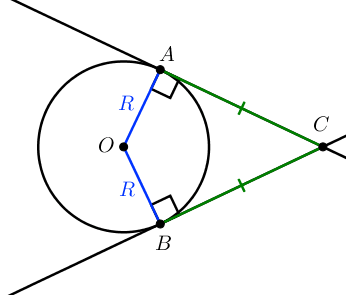
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3: Касательная перпендикулярна радиусу, проведенному к точке касания.

Интересные факты о дугах

1. Дуги могут быть закрытыми или открытыми. Закрытая дуга образует круг или окружность, а открытая дуга имеет начальную и конечную точки.
2. Угол между линией, соединяющей начальную и конечную точки дуги, и продолжением линии, проходящей через центр окружности, называется центральным углом дуги.
3. Дуги могут измеряться в радианах или градусах. Радиан – это единица измерения, которая определяется соотношением длины дуги и радиуса окружности.
4. У дуги есть длина, которая выражается в единицах измерения длины (сантиметрах, метрах и т.д.). Длина дуги зависит от размера угла и радиуса окружности.
5. Дуги используются в архитектуре и дизайне для создания красивых форм и линий. Они могут быть использованы в декоративных элементах, фресках и скульптуре.
6. В музыке термин «дуга» используется для обозначения движения смычка по струне музыкального инструмента. Это движение создает звук.
7. В промышленности дуги используются для сварки. Сварочная дуга – это электрический разряд между электродом и сварочным материалом.

Таким образом, дуги являются универсальными геометрическими объектами, которые присутствуют в различных сферах нашей жизни и придают им красоту и функциональность.

Определение круга

Круг — это геометрическая фигура, которая представляет собой множество точек, расположенных на одной плоскости и равноудаленных от одной точки, называемой центром круга.

Круг имеет следующие особенности:

• Все точки на окружности круга равноудалены от его центра;
• Диаметр круга является отрезком, соединяющим любые две точки его окружности и проходящим через центр;
• Радиус круга — это половина его диаметра;
• Периметр круга — это сумма длин всех отрезков, из которых состоит его окружность;
• Площадь круга — это мера его поверхности, равная произведению числа пи на квадрат радиуса.

Круг является одним из основных геометрических понятий и широко используется в различных областях знания, включая математику, физику, инженерию и архитектуру.

Radius[edit]

The product of the line segments AP and PB equals the product of the line segments CP and PD. If the arc has a width AB and height CP, then the circle’s diameter

Using the intersecting chords theorem (also known as power of a point or secant tangent theorem) it is possible to calculate the radius r of a circle given the height H and the width W of an arc:

Consider the chord with the same endpoints as the arc. Its perpendicular bisector is another chord, which is a diameter of the circle. The length of the first chord is W, and it is divided by the bisector into two equal halves, each with length W2. The total length of the diameter is 2r, and it is divided into two parts by the first chord. The length of one part is the sagitta of the arc, H, and the other part is the remainder of the diameter, with length 2r − H. Applying the intersecting chords theorem to these two chords produces

whence

so

Отличие круга и окружности

Круг — это геометрическая фигура, которая представляет собой множество всех точек на плоскости, находящихся на равном расстоянии от центра. В отличие от окружности, круг не имеет никаких ограничений, поэтому он не имеет начала и конца. Круг используется в математических и геометрических задачах, а также в различных технических решениях.

Окружность — это геометрическая фигура, состоящая из всех точек на плоскости, находящихся на одинаковом расстоянии от центра. Окружность имеет определенный размер, в отличие от круга, который может быть любого размера. Окружность является одной из наиболее изученных геометрических фигур и используется в различных областях, включая математику, физику, а также в технических расчетах и инженерных конструкциях.

Основное отличие между кругом и окружностью заключается в том, что круг — это бесконечное множество точек на плоскости, в то время как окружность ограничена определенным размером и имеет конкретные параметры, такие как радиус и диаметр.

Кроме того, окружность может быть использована для определения цилиндра и сферы, в то время как круг используется только для двумерных объектов. В математических вычислениях и геометрических задачах точность и различение между кругом и окружностью может быть ключевым фактором.

Понятие круга и окружности

Круг и окружность — два основных понятия геометрии, связанных между собой. Они имеют некоторые сходства, но также отличаются друг от друга.

Круг — это геометрическая фигура, которая представляет собой множество всех точек плоскости, расстояние от которых до центра круга не превышает радиуса. Круг не имеет начала и конца, потому что он бесконечен.

Круг можно представить себе как закрашенную плоскость, ограниченную кривой линией, все точки которой находятся на одном и том же расстоянии от центра.

Важно отметить, что понятие круга используется как в геометрии, так и в аналитической геометрии. Окружность — это частный случай круга

Она также представляет собой множество всех точек плоскости, расстояние от которых до центра окружности равно радиусу. Окружность является закрытой кривой линией, без начала и конца, ограничивающей плоскую фигуру

Окружность — это частный случай круга. Она также представляет собой множество всех точек плоскости, расстояние от которых до центра окружности равно радиусу. Окружность является закрытой кривой линией, без начала и конца, ограничивающей плоскую фигуру.

В отличие от круга, окружность имеет конкретные граничные точки, которые находятся на одном и том же расстоянии от центра окружности. Окружность можно представить себе как дугу, полученную поворотом круга на определенный угол вокруг его центра.

Таким образом, круг и окружность являются связанными понятиями, но окружность является частным случаем круга, где радиус окружности равен ее диаметру. Круг и окружность находят широкое применение в различных областях, таких как геометрия, физика, инженерия и т. д.

Зависимость между углами, дугами и хордами

Теорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги.

Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны:

∠AOB = ∠A’O’B’.

Требуется доказать, что ◡AB = ◡A’B’.

Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами.

Теорема 58 (обратная 57). Равным дугам соответствуют равные углы.

Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88).

Требуется доказать, что ∠AOB = ∠A’O’B’.

Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно,

∠AOB = ∠A’O’B’ (ЧТД).

Теорема 59. Диаметр больше всякой хорды.

Даны диаметр CD и хорда MN (черт. 87).

Требуется доказать, что CD > MN.

Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN

MON > MN или MO + ON > MN

Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства:

CO + OD > MN или CD > MN (ЧТД).

Теорема 60. Равные хорды стягивают равные дуги.

Даны равные хорды AB и CD (черт. 89) (AB = CD).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Соединив точки A, B, C, D с центром, имеем

∆AOB = ∆COD, ибо

OA = OC и OB = OD как радиусы, AB = CD по условию.

Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД).

Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами.

Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD).

Требуется доказать, что AB = CD.

Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД).

Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда.

Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC).

Требуется доказать, что BD > AC.

Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД).

Теорема 63 (обратная 62). Против большей хорды лежит большая дуга.

Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC).

Требуется доказать, что ◡BD > ◡AC.

Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД).

Площадь сектора

Напомним, что сектором называется часть круга, образованная двумя его радиусами. Если же в круге проведена хорда, то она отсекает от него сегмент:

Проведем из центра окружности 360 радиусов, причем угол между соседними радиусами будет ровно 1°. В результате мы разобьем окружность на 360 одинаковых секторов, площадь каждого такого сектора будет в 360 раз меньше площади круга:

Теперь рассмотрим сектор, который образован дугой величиной в α градусов. Если α – целое число, то такой сектор можно составить из α секторов, каждый из которых составляет по 1°. Тогда площадь сектора круга будет определяться формулой:

Задание. Круговой сектор опирается на дугу в 45°, а его радиус составляет 40. Определите площадь этого сектора.

Решение. Используем выведенную формулу:

Ответ: 12,5π.

Задание. Площадь сектора равна 200 см2. Он опирается на дугу в 30°. Каков радиус кругового сектора? При решении примите π равным 3,14.

Решение. Из формулы площади сектора выразим радиус окружности:

Ответ: ≈ 27,6 см.

Задание. На сторонах произвольного прямоугольника построены полукруги:

Докажите, что площадь полукруга, опирающегося на полуокружность, равна сумме площадей полукругов, опирающихся на катеты.

Решение. Полукруг представляет собой сектор с центральным углом α = 180°, поэтому его площадь может быть рассчитана так:

Заметим, что эти стороны являются диаметрами полукругов. Обозначим как D₁ диаметр полукруга, опирающегося на гипотенузу, а два других диаметра как D₂ и D₃. Тогда можно выполнить преобразования:

Именно это равенство нам и требовалось доказать.

Теперь рассмотрим более сложную задачу, в которой необходимо определить площадь сегмента.

Задание. В окружности радиусом 20 проведена хорда длиной 12. Она разбивает окружность на два круговых сегмента. Найдите площадь каждого из них. При расчете примите π ≈3,14.

Чтобы найти площадь меньшего сегмента, можно вычесть из площади кругового сектора площадь треугольника АВО. Для нахождения обоих площадей в любом случае надо сначала определить величину угла ∠АОВ. Это можно сделать, применив теорему косинусов:

Далее надо рассчитать площадь ∆АВС. Это можно сделать с помощью разных формул, мы используем формулу с синусом угла. Для этого предварительно вычислим синус ∠АОВ, применив основное тригонометрическое тождество:

Осталось вычесть из площади сектора площадь ∆АВС, чтобы найти площадь кругового сегмента S₁:

Примечание. В подобных задачах ответы и промежуточные ответы могут немного отличаться в зависимости от того, с какой точностью берется число π, вычисляется ∠АОВ и его синус, и как именно округляются промежуточные результаты и т. п. Более точные расчеты показывают, что в описанной задаче величины S₁ и S₂ примерно равны:

Дуги окружности

Длина дуги окружности

Длина (точнее, длина дуги ) дуги окружности радиусом r, соединяющей угол θ (измеренный в радианах) с центром окружности, т. Е. Центральный угол , составляет

L = θ r. { displaystyle L = theta r.}

Это потому, что

L c i r c u m f e r e n c e = θ 2 π. { displaystyle { frac {L} { mathrm {окружность}}} = { frac { theta} {2 pi}}.}

Подставляем в окружность

L 2 π r = θ 2 π, { displaystyle { frac {L} {2 pi r}} = { frac { theta} {2 pi}},}

и, где α — тот же угол, измеренный в градусах, поскольку θ = α / 180π, длина дуги равна

L = α π r 180. { displaystyle L = { frac { alpha pi r} {180}}.}

Практический способ определить длину дуги в окружности — построить две линии от ее концов до центра окружности, измерьте угол, под которым две прямые пересекаются с центром, затем решите для L, перемножив выражение:

мера угла в градусах / 360 ° = L / окружность.

Например, если угол составляет 60 градусов, а длина окружности — 24 дюйма, то

60 360 = L 24 360 L = 1440 L = 4. { displaystyle { begin {align} { frac {60 } {360}} = { frac {L} {24}} \ 360L = 1440 \ L = 4. End {align}}}

Это так, потому что длина окружности и градусы круга, которых всегда 360, прямо пропорциональны.

Верхняя половина круга может быть параметризована как

y = r 2 — x 2. { displaystyle y = { sqrt {r ^ {2} -x ^ {2}}}.}

Тогда длина дуги из x = a { displaystyle x = a}

L = r ab. { displaystyle L = r { Big } _ {a} ^ {b}.}

Площадь сектора дуги

Площадь сектора, образованного дугой и центром круга (ограниченного дугой и двумя радиусами, проведенными к ее конечным точкам), составляет

A = r 2 θ 2. { displaystyle A = { frac {r ^ {2} theta} {2}}.}

Область A имеет ту же пропорцию к площади круга , что и угол θ до полного круг:

A π r 2 = θ 2 π. { displaystyle { frac {A} { pi r ^ {2}}} = { frac { theta} {2 pi}}.}

Мы можем сократить π с обеих сторон:

A г 2 = θ 2. { displaystyle { frac {A} {r ^ {2}}} = { frac { theta} {2}}.}

Умножая обе стороны на r, мы получаем окончательный результат:

А = 1 2 г 2 θ. { displaystyle A = { frac {1} {2}} r ^ {2} theta.}

Используя преобразование, описанное выше, мы находим, что площадь сектора для центрального угла, измеренная в градусах, равна

А = α 360 π r 2. { displaystyle A = { frac { alpha} {360}} pi r ^ {2}.}

Площадь сегмента дуги

Площадь фигуры, ограниченная дугой и прямой линией между двумя его конечными точками находится

1 2 r 2 (θ — sin ⁡ θ). { displaystyle { frac {1} {2}} r ^ {2} left ( theta — sin { theta} right).}

Чтобы получить площадь дугового сегмента , нам нужно вычесть площадь треугольника, определяемую центром круга и двумя конечными точками дуги, из площади A { displaystyle A}

Радиус дуги

CD = AP ⋅ PBCP + CP { displaystyle CD = { frac {AP cdot PB} {CP}} + CP}

Использование теорема о пересечении хорд (также известная как степень точки или теорема о секущем касательном) позволяет вычислить радиус r окружности с учетом высоты H и ширины W arc:

Рассмотрим хорду с теми же конечными точками, что и дуга. Его серединный перпендикуляр — это еще одна хорда, которая равна диаметру окружности. Длина первой хорды равна W, и она делится биссектрисой на две равные половины, каждая длиной W / 2. Общая длина диаметра составляет 2r, и он делится на две части первой хордой. Длина одной части — это стрела дуги, H, а другая часть — это остаток диаметра, длиной 2r — H. Применение теоремы о пересечении хорд к этим двум хордам дает

H (2 r — H) = (W 2) 2, { displaystyle H (2r-H) = left ({ frac {W} {2}} right) ^ {2},}

откуда

2 r — H = W 2 4 H, { displaystyle 2r-H = { frac {W ^ {2}} {4H}},}

поэтому

r = W 2 8 H + H 2. { displaystyle r = { frac {W ^ {2}} {8H}} + { frac {H} {2}}.}

Пример 2

Найдите длину эллиптической дуги, показанной на рисунке 8, зная большую полуось r и малую полуось s эллипса.

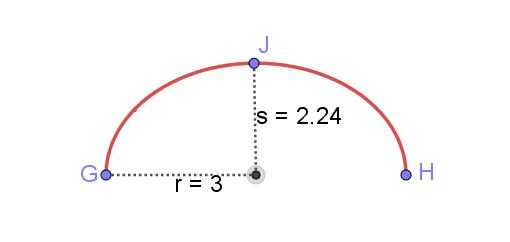
Рисунок 8. Эллиптическая арка между GH. Подготовил Рикардо Перес.

Определение длины эллипса долгое время было одной из самых сложных задач математики. Вы можете получить решения, выраженные эллиптическими интегралами, но чтобы получить числовое значение, вы должны разложить эти интегралы в степенные ряды. Для точного результата потребовалось бы бесконечное количество членов этих рядов.

К счастью, индуистский математический гений Рамануджан, живший между 1887 и 1920 годами, нашел формулу, которая очень точно аппроксимирует периметр эллипса:

Периметр эллипса с r = 3 см и s = 2,24 см составляет 16,55 см. Однако показанная эллиптическая дуга имеет половину этого значения:

Длина эллиптической арки GH = 8,28 см.