Минимум по геометрии 8 класса. модуль 1 для школьников

Внедрение геометрических принципов в реальный мир

Геометрия является одной из фундаментальных наук, которая изучает пространственные формы и их свойства. Применение геометрических принципов находит свое применение в различных областях, включая архитектуру, строительство, дизайн, инженерию и даже в ежедневной жизни.

Принципы геометрии помогают нам анализировать объекты и структуры, предсказывать их поведение и оптимизировать различные процессы. Они также дают нам понимание о том, как определенная форма или структура влияет на функциональность и эстетику объекта.

Давайте рассмотрим несколько примеров, как геометрические принципы применяются в реальном мире:

Архитектура: Геометрия играет ключевую роль в создании и проектировании зданий и сооружений. Архитекты используют принципы симметрии, пропорций и гармонии, чтобы создать привлекательные и функциональные структуры. Например, в планировании зданий используются различные геометрические формы, такие как круги, квадраты и треугольники, чтобы создать устойчивую и эстетически приятную конструкцию.
Дизайн: Геометрические принципы используются при создании дизайна различных объектов и предметов. Дизайнеры используют принципы симметрии, равновесия и пропорций для создания эстетически приятных и функциональных объектов. Геометрические формы также могут использоваться для создания паттернов и узоров на тканях, обоях и других поверхностях.
Инженерия: Геометрические принципы широко применяются в инженерных расчетах и конструкциях. Например, треугольники играют важную роль в статическом анализе и силовых расчетах. Принципы геометрии также применяются в проектировании дорог, мостов, тоннелей и других инфраструктурных объектов.

Вышеперечисленные примеры демонстрируют, как геометрия проникает в различные сферы нашей жизни. Понимание и применение геометрических принципов помогает нам не только создавать красивые и функциональные объекты, но и улучшать и оптимизировать процессы в различных областях.

Отношения

Изометрические треугольники

Два треугольника называются изометричными , накладываемыми друг на друга или, ранее, равными , если они имеют одинаковую длину сторон. В этом случае можно сделать так, чтобы вершины одного соответствовали вершинам другого с помощью изометрии (например, сдвига , поворота или симметрии ), и это соответствие затем соединяет углы одной и той же меры. Следовательно, эти треугольники также имеют одинаковую площадь.

Это первое определение эквивалентно каждому из следующих трех:

три длины сторон первого треугольника такие же, как и у второго (сокращенно CCC);
два треугольника имеют угол одинакового измерения между двумя сторонами одинаковой длины (сокращенно CAC);
два треугольника имеют стороны одинаковой длины между двумя углами одинаковых размеров (сокращенно ACA).

Подобные треугольники

Два треугольника с одинаковыми углами называются подобными . Они не обязательно изометричны, но их длины сторон пропорциональны с тем же коэффициентом пропорциональности k . Тогда их площади связаны коэффициентом k 2 .

Действительно, есть сходство (которое представляет собой соединение изометрии и гомотетии), которое превращает одно в другое. Это определение эквивалентно:

три угла первого имеют те же размеры, что и размеры второго (сокращенно ААА) (на самом деле двух углов достаточно: третий выводится из него)

или в:

три длины сторон первого пропорциональны сторонам второго.

Два изометрических треугольника всегда одинаковы. Также два равносторонних треугольника (не обязательно изометрических).

Значение в повседневной жизни

Понятие «наклонная» имеет важное значение не только в геометрии, но и в повседневной жизни. Изучение наклонной плоскости и соответствующих ей понятий помогает нам понять и описать различные объекты и явления, с которыми мы сталкиваемся ежедневно

К примеру, при строительстве дома или постройке различных конструкций, знание понятия «наклонная» помогает инженерам и строителям правильно прокладывать фундамент, строить стены и крыши с нужным уклоном. Без знания геометрических принципов наклонных плоскостей, работа строителей могла бы быть неправильной, что в свою очередь привело бы к серьезным проблемам и повреждениям в будущем.

Также, понятие «наклонная» используется при изучении и применении геодезических технологий. Геодезисты используют основные принципы наклонных плоскостей при построении карт и измерении равнинных площадей. Знание наклонных плоскостей помогает им корректно устанавливать опорные точки и производить точные измерения, что является необходимым для учёта и анализа местности.

Значение понятия «наклонная» также распространяется на повседневную жизнь каждого из нас. Например, при выборе спуска по склону горы на лыжах или сноуборде, нам необходимо учесть угол наклона, чтобы избежать возможных опасностей и травматических ситуаций. Также, при выборе места для отдыха или пикника, наклон поверхности может оказывать влияние на качество отдыха и комфортность проведения времени.

Итак, понимание понятия «наклонная» в геометрии имеет большое значение не только в учебе, но и в реальной жизни. Оно позволяет нам более глубоко и точно понимать окружающий нас мир, применять полученные знания в различных областях деятельности и принимать правильные решения на практике.

Расчет диагонали при неизвестных сторонах треугольника

В некоторых случаях задача определения диагонали треугольника может быть затруднительной, особенно, если неизвестны некоторые стороны треугольника.

Кроме формул, позволяющих вычислить диагональ, зная длины сторон, существуют способы расчета диагонали при неизвестных сторонах треугольника.

Один из таких способов — использование теоремы косинусов. Для этого необходимо знать угол между двумя неизвестными сторонами и длины остальных сторон треугольника. Затем можно применить формулу:

d = √

где d — длина диагонали, a и b — длины неизвестных сторон, α — угол между этими сторонами.

Если угол между неизвестными сторонами неизвестен, его можно вычислить, используя другую известную формулу, например, теорему синусов:

sin(α) = (a sin(β)) / d

где β — угол между диагональю и одной из известных сторон.

Еще один способ — использование пропорций. Для этого необходимо знать отношение длины диагонали к длине одной из сторон треугольника. Например, если известно, что диагональ равна половине длины одной из сторон, можно применить пропорцию:

диагональ/d = 1/2

⇒

d = 2a/√3

где a — длина стороны, которую необходимо умножить на коэффициент 2/√3.

Основные линии треугольника

Медиана

Медиана треугольника — это отрезок, соединяющий верщину треугольника
с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую
из них в отношении 2:1, считая от вершины. Эта точка называется центром
тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих
треугольников.

Биссектриса

Биссектриса
угла — это луч, который исходит из его вершины, проходит между его
сторонами и делит данный угол пополам. Биссектрисой треугольника называется
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на
противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Биссектриса угла — это геометрическое место точек, равноудаленных от
сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону
на отрезки, пропорциональные прилегажащим сторонам: .
Точка пересечения биссектрис треугольника является

Высота

Высотой
треугольника называется перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В высота, проведенная
из вершины прямого угла, разбивает его на два треугольника,
исходному.
В две его
высоты отсекают от него треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют
серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов
этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная
от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам
треугольника, является центром .

Средняя линия

Средней
линией треугольника называется отрезок, соединяющий середины двух его
сторон.

Пример решения

Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:

Другие стороны.
Значения диагоналей.
Площадь.
R описанной окружности через площадь и периметр.
Выяснить возможность укладки плитки в форме квадрата на такую поверхность.
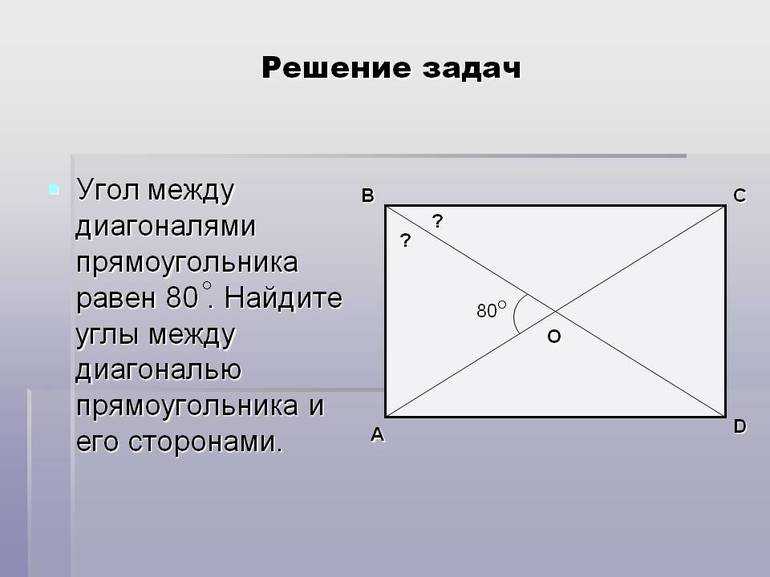
Вычислить значения всех углов между смежными сторонами.

Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.

У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.)

Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки

Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.

Значение диагоналей находится по формуле: d = ^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 . Радиус вычисляется так:

R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).
R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).

Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.

Определение и основные понятия

Важным понятием, связанным с диагональю треугольника, является высота. Высота — это отрезок, соединяющий вершину треугольника с противолежащей ей стороной, перпендикулярный этой стороне.

Для нахождения диагонали в треугольнике, можно использовать теорему Пифагора. Она гласит, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов. В случае треугольника, где стороны не являются прямыми, применяются другие методы и формулы.

Шаги для нахождения длины диагонали

Найдите две известные стороны треугольника.

Возведите каждую сторону в квадрат.

Сложите квадраты двух известных сторон.

Найдите квадратный корень от суммы квадратов.

Полученное число будет длиной диагонали треугольника.

Примеры нахождения диагонали треугольника 4 класс

Для того чтобы найти диагональ в треугольнике, мы должны знать длины двух его сторон и угол между ними.

Рассмотрим конкретный пример: у нас есть треугольник ABC, где сторона AB равна 5 см, сторона BC равна 4 см, а угол между ними равен 60 градусов.

Для начала, строим треугольник ABC на листе бумаги, используя линейку и угольник. Затем отмечаем стороны AB и BC, и находим их длины с помощью линейки. Также отмечаем угол между этими сторонами.

Далее, используя изученные правила, находим диагональ AC. Для этого можно использовать теорему косинусов. Формула для нахождения диагонали AC выглядит следующим образом:

AC = √(AB² + BC² — 2 * AB * BC * cos(угол АСВ))

Подставляя известные значения, получаем:

AC = √(5² + 4² — 2 * 5 * 4 * cos(60))

AC = √(25 + 16 — 40 * 0.5)

AC = √(25 + 16 — 20)

AC = √(41 — 20)

AC = √21

Таким образом, диагональ AC треугольника ABC равна √21 см.

При решении других примеров нахождения диагонали треугольника 4 класс, нужно использовать аналогичные шаги и вычисления

Очень важно правильно указывать единицы измерения и ясно обозначать углы, стороны и диагонали на рисунке треугольника. Это поможет избежать путаницы и сделать решение задачи более понятным

Расчет диагонали при известных сторонах треугольника

Для вычисления диагонали можно использовать различные формулы в зависимости от известных параметров треугольника. Если известны длины всех трех сторон, то можно воспользоваться формулой герона.

Формула герона имеет вид:

Вычисляем полупериметр треугольника p = (a + b + c) / 2, где a, b и c — длины сторон;
Находим площадь треугольника по формуле S = √(p(p — a)(p — b)(p — c));
Диагональ d вычисляется по формуле d = 2√2S / a.

Если известны длины двух сторон и угол между ними, то можно воспользоваться формулой косинусов. Формула косинусов имеет вид:

Вычисляем косинус угла между известными сторонами по формуле cos(α) = (b2 + c2 — a2) / 2bc, где a — неизвестная сторона;
Вычисляем синус угла по формуле sin(α) = √(1 — cos2(α));
Вычисляем диагональ по формуле d = 2bcsin(α) / a.

Если известны длины смежных сторон и угол между ними, то можно воспользоваться формулой синусов:

Вычисляем синус угла по формуле sin(α) = a / c, где c — неизвестная сторона;
Вычисляем диагональ по формуле d = 2bcsin(α) / a;

Используя эти формулы, можно рассчитать диагональ треугольника при известных параметрах.

Четырехугольники

Сумма углов четырехугольника равна 360°.
Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
В параллелограмме противолежащие углы равны.
В параллелограмме противолежащие стороны равны.
В параллелограмме сумма смежных углов равна 180°.
Если диагонали параллелограмма являются биссектрисами углов, из которых они выходят, этот параллелограмм является ромбом.
Если в параллелограмме диагонали равны, этот параллелограмм является прямоугольником.
Если в прямоугольнике диагонали перпендикулярны, этот прямоугольник является квадратом.
Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Диагонали ромба перпендикулярны.
Диагонали квадрата взаимно перпендикулярны.
Диагонали квадрата делят его углы пополам.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Площадь параллелограмма равна произведению смежных сторон на синус угла между ними.
Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
Площадь ромба равна половине произведения диагоналей.
Площадь квадрата равна произведению двух его смежных сторон.
Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если диагонали ромба равна 3 и 4, то его площадь равна 6.
Трапеция – четырехугольник две стороны которого параллельны, а две другие нет.
У равнобедренной трапеции диагонали равны.
У равнобедренной трапеции углы при основании равны.
Средняя линия трапеции параллельна основаниям.
Средняя линия трапеции равна полусумме оснований.
Площадь трапеции равна произведению полусуммы оснований на высоту.
Площадь трапеции равна произведению средней линии на высоту.
Площадь трапеции меньше произведения суммы оснований на высоту.

Другие результаты

Теорема Фалеса соединяет длины сторон двух одинаковых треугольников, имеющих общую вершину и параллельные противоположные стороны.

Теорема Наполеона утверждает, что центры равносторонних треугольников, образованных снаружи на сторонах треугольника, сами являются вершинами равностороннего треугольника.

« Японская теорема Карно » устанавливает, что сумма радиусов вписанной и описанной окружностей равна сумме расстояний от центра описанной окружности до сторон треугольника.

Теорема Менелая дает необходимое и достаточное условие для совмещения трех точек, выровненных соответственно со сторонами треугольника.

Теорема Морли гласит, что пересечения углов триссектрис треугольника образуют равносторонний треугольник.

Теорема Нагеля показывает, что угол треугольника, деленный пополам, совпадает с углом, в котором верхние стороны проходят через ортоцентр и центр описанной окружности.

Теорема Нойберга устанавливает, что центры трех квадратов, полученных с помощью определенного геометрического построения треугольника, являются центрами сторон треугольника.

Теорема Гамильтона утверждает, что круг Эйлера одинаков для четырех треугольников, образованных ортоцентрической группой.

Теорема Эйлера в геометрии выражает расстояние d между центрами вписанной и описанной окружностей согласно их соответствующим радиусам r и R как d 2 = R ( R -2 r ) . Отсюда следует, что радиус вписанной окружности как минимум вдвое меньше, чем радиус описанной окружности (неравенство Эйлера).

С céviennes

Теорема Ceva дает необходимое и достаточное условие для трех прямых линий (называемые céviennes ) , соответственно , проходящих через три вершины треугольника параллельны или одновременно.

Теорема Gergonne затем дает соотношение между длиной céviennes и длин линий , соединяющих их пересечение в вершинах.

Теорема Стюарта связывает длину чевиана с длинами сторон двух образующихся треугольников.

В теореме Terquem показывает , что педаль окружность , треугольник , образованный три PDAL футов céviennes пересекающихся, резка стороны треугольника в трех точках , которые также ноги céviennes одновременно.

Теорема Рауса дает профакторизовали поверхности между площадью треугольника , образованного тремя céviennes, и что из данного треугольника.

С кругами

Теорема о шести кругах показывает, что последовательность окружностей, последовательно касающихся снаружи и касательных внутрь к двум сторонам треугольника (стороны которых меняются круговой перестановкой), является 6-периодической.

Обратное к теореме Микеля о трех окружностях показывает, что три окружности, проходящие соответственно через вершины треугольника и секущую вдоль соответствующих сторон, совпадают в точке, называемой точкой Микеля.

Все основные формулы треугольника

Рассмотрим формулы, по которым можно вычислить площадь треугольника:

Вместо стороны A могут быть и показатели других сторон.

Рассмотрим также подобия треугольников.

Таким образом, треугольник ABC будет подобен MNK. Так угол альфа будет равен углу альфа1, угол бета будет равен углу бета1, угол гамма будет равен углу гамма1. Иначе ABMN будет равно BCNK будет равно ACMK будет равно k.

Коэффициент k = коэффициент подобия.

Рассмотрим признаки подобия треугольников:

Первый признак подобия треугольника. В случае, если два угла треугольника равны соответственно двум углам другого треугольника, то такие треугольники называются подобными.
Второй признак подобия фигур. В случае, если три стороны данной фигуры пропорциональны трем сторонам другой фигуры (треугольника), то такие треугольники называют подобными.
Третий признак подобия треугольника. В случае, если две стороны треугольника будут пропорциональны двум сторонам другого треугольника, а углы, которые расположены между этими сторонами, являются равными, то такими треугольники называются подобными.

Посмотрите на вписанную окружность:

Основные свойства вписанной окружности:

Центр вписанной окружности всегда расположен на пересечении биссектрис внутренних углов треугольника.
В любой треугольник возможно вписать окружность, но только одну.

Виды треугольников

По свойствам углов выделяют три вида треугольников:

Остроугольный. Все его углы являются острыми.
Прямоугольный. Только один угол является прямым (то есть, он равен 90 градусам).
Тупоугольный. Один угол является тупым.

Рассмотрим внешний вид данных треугольников:

По свойствам сторон выделяют:

Равнобедренный.
Равносторонний.
Прямоугольный.

И остроугольный, и тупоугольный, и прямоугольный треугольники могут быть равнобедренными.

Посмотрите на рисунки равнобедренных треугольников:

Рассмотрим свойства равнобедренных треугольников:

Углы при основании будут всегда равны.
Высота, медиана, биссектриса, которые проводятся в равнобедренном треугольнике к основанию, будут совпадать.

Как найти площадь данной фигуры?

Рассмотрим свойства данной фигуры:

Совокупность двух острых углов будет равна 90 градусам.
Катет, который лежит напротив угла в 30 градусов, будет равен половине гипотенузы.
Соответственно, если катет = половина гипотенузы, то этот катет лежит напротив угла в 30 градусов.
Медиана, которая проведена из вершины угла прямого, будет равна половине гипотенузы.

История

R49 → R55 проблемы папируса Райнда .

Фигура треугольника, представленная в задаче R51 папируса Райнда .

Никаких математических документов из Древнего Царства до нас не дошло. Но монументальная архитектура династий III E и IV E свидетельствует о том, что египтяне того времени обладали относительно сложными познаниями в геометрии, особенно в изучении треугольников.

Расчет площади этого рисунка изучается в задачах R51 папируса Райнда , M4, M7 и M17 папируса Москвы и всех датируемых Средним царством . Задача R51 представляет собой первое письменное свидетельство в мировой истории математики о вычислении площади треугольника.

Описание проблемы Rhind Papyrus R51

Термин мрыт, вероятно, означает высоту или сторону. Но формула, используемая для вычисления площади, склоняет интерпретацию в пользу первого решения. Писец взял половину основания треугольника и вычислил площадь прямоугольника, образованного этой стороной, и высоту, т.е.

Взнак равнобвsе2мрут{\ displaystyle A = {\ frac {base} {2}} {mryt}}

эквивалентно общей формуле, используемой сегодня:

Sзнак равновчас2.{\ displaystyle S = {\ frac {ah} {2}}.}

Евклид в книге I своих Элементов , около -300, утверждает свойство на сумме углов треугольника и трех случаях равенства треугольников (см. Выше абзац об изометрических треугольниках).