Чему равен коэффициент упругости?

Формулы расчета пружин растяжения

Основные понятия

Пружина растяжения — это спирально-цилиндрическая пружина, витки которой прилегают друг к другу. Пружина подвергается действию противоположно направленных усилий, приложенных вдоль ее оси.

Размеры

d	диаметр проволоки
D	средний диаметр пружины
D1	наружный диаметр пружины
D2	внутренний диаметр пружины
H	рабочая деформация
t	шаг активных витков в ненагруженном состоянии
o	высота ушка
sx	деформация пружины
Lx	длина пружины
Fx	рабочая сила, действующая на пружину
W8	энергия деформации
x	индекс, обозначающий состояние пружины

Навивка

1. Вправо (стандарт)

2. Влево (должна отображаться соответствующая надпись)

Состояния

1. Свободное: пружина не нагружена (индекс 0)

2. Предварительная нагрузка: пружина с минимальной рабочей нагрузкой (индекс 1)

3. Полная нагрузка: пружина с максимальной рабочей нагрузкой (индекс

4. Предел: пружина вдавлена до касания витков (индекс 9).

Зацепы пружин растяжения

Высота зацепа пружины растяжения

Где:

L0	длина пружины в свободном состоянии
LZ	длина части пружины с витками

Часто используемые зацепы пружин растяжения

Тип зацепа и информация о размерах	Изображение
Половина витка, o = 0,55…0,8 D2
Обычно d ≤ 6,3 мм, D >= 3,15 мм, i >= 9
Полный виток, o = 0,8…1,1 D2
Используется без ограничений
Полный виток сбоку, o » D2
Когда нагрузка не обязательно должна прикладываться по оси
Полный виток внутри, o = 1,05…1,2 D2
Обычно d ≥ 10 мм, i >= 7
Поднятый зацеп, o = 1,2 D2 … 30 d
Обычно для d = от 0,5мм до 4 мм, o ≤ 100 мм
Два полных витка, o »D
Используется без ограничений
Два полных витка сбоку, o » D2
Когда нагрузка не обязательно должна прикладываться по оси

Расчет пружин в метрических единицах

Общие формулы расчета

Коэффициент использования материала

Наружный диаметр пружины

D1 = D + d

Где:

D	средний диаметр пружины
d	диаметр проволоки

Внутренний диаметр пружины

D2 = D — d

Где:

D	средний диаметр пружины
d	диаметр проволоки

Рабочая деформация

H = L81= s81

Где:

L8	длина полностью нагруженной пружины
L1	длина предварительно нагруженной пружины
s8	деформация полностью нагруженной пружины
s1	деформация предварительно нагруженной пружины

Высота зацепа пружины

Где:

L0	длина пружины в свободном состоянии
LZ	длина части пружины с витками

Индекс пружины

c = D/d

Где:

D	средний диаметр пружины
d	диаметр проволоки

Поправочный коэффициент Валя

Где:

c	индекс пружины
LZ	длина части пружины с витками

Начальное растяжение

Где:

Определение коэффициента жесткости

Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:

k = F/x.

Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.

Единица измерения жесткости в СИ — Н/м.

Физические характеристики пружин

Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:

1. материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
2. диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
3. форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
4. длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Требуется вычитка, рецензия учебной работы? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.

Какие бывают типы пружин

В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.

Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.

Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.

В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.

Примеры задач с решением

Пример 1

Задание.
Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $\frac{Н}{м}.\ $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

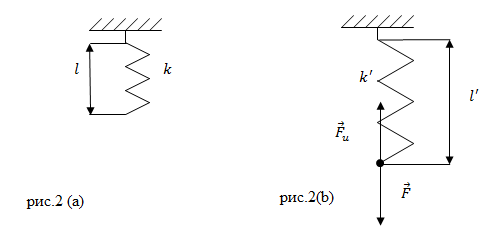
Решение.
Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:

При упругих деформациях выполняется закон Гука:

Из (1.2) найдем удлинение пружины:

\

Длина растянутой пружины равна:

Вычислим новую длину пружины:

Ответ.
1) $k»=10\ \frac{Н}{м}$; 2) $l»=0,21$ м

Пример 2

Задание.
Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $\Delta l_2$?

Решение.
Если пружины соединены последовательно, то деформирующая сила ($\overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:

Для второй пружины запишем:

Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:

Из равенства (2.3) получим удлинение первой пружины:

\

Ответ.
$\Delta l_1=\frac{k_2\Delta l_2}{k_1}$

Груз, подвешенный на пружине, вызывает ее деформацию. Если пружина способна восстановить первоначальную форму, то ее деформация называется упругой.

При упругих деформациях выполняется закон Гука:

где F упр ¾ сила упругости; k
¾ коэффициент упругости (жесткость); Dl
— удлинение пружины.

Примечание
: знак “-” определяет направление силы упругости.

Если груз находится в равновесии, то сила упругости численно равна силе тяжести: k
Dl
= m g
, тогда можно найти коэффициент упругости пружины:

где m
¾ масса груза; g
¾ ускорение свободного падения.

Рис.1		Рис. 2

При последовательном соединении пружин (см. рис.1) силы упругости, возникающие в пружинах, равны между собой, а общее удлинение системы пружин складывается из удлинений в каждой пружине.

Коэффициент жесткости такой системы определяется по формуле:

где k
1 — жесткость первой пружины; k
2 — жесткость второй пружины.

При параллельном соединении пружин (см. рис. 2) удлинение пружин одинаково, а результирующая сила упругости равна сумме сил упругости в отдельных пружинах.

Коэффициент жесткости при параллельном соединении пружин находится по формуле:

k
рез = k
1 + k
2 . (3)

Порядок выполнения работы

1. Прикрепить пружину к штативу. Подвешивая к каждой пружине грузы в порядке возрастания их массы, измерять удлинение пружины Dl
.

2. По формуле F
= mg
рассчитать силу упругости.

3. Построить графики зависимости силы упругости от величины удлинения пружины. По виду графиков определить выполняется ли закон Гука.

5. Найти абсолютную погрешность каждого измерения

Dk i
= êk i
— k
ср ê.

6. Найти среднее арифметическое значение абсолютной погрешности D k
ср.

7. Результаты измерений и расчетов занести в таблицу.

1. Провести измерения (как описано в задании 1) и рассчитать коэффициенты упругости последовательно и параллельно соединенных пружин.

2. Найти среднее значение коэффициентов и погрешности их измерений. Результаты измерений и вычислений занести в таблицу.

4. Найти погрешность эксперимента, сравнив теоретические значения коэффициента упругости с экспериментальными по формуле:

.

m , кг
F , Н
Первая пружина
Dl 1 , м
k 1 , Н/м							k ср =
D k 1 , Н/м							D k ср =
Вторая пружина
Dl 2 , м
k 2 , Н/м							k ср =
D k 2 , Н/м							D k ср =
Последовательное соединение пружин
Dl , м
k , Н/м							k ср =
D k , Н/м							D k ср =
Параллельное соединение пружин
Dl , м
k , Н/м							k ср =
D k , Н/м							D k ср =

Контрольные вопросы

Сформулируйте закон Гука.

Дайте определение деформации, коэффициента упругости. Назовите единицы измерения этих величин в СИ.

Как находится коэффициент упругости для параллельного и последовательного соединения пружин?

Лабораторная работа № 1-5

Изучение законов динамики

Поступательного движения

Теоретические сведения

Динамика
изучает причины, вызывающие механическое движение.

Инерция
— способность тела сохранять состояние покоя или прямолинейного равномерного движения, если на это тело не действуют другие тела.

Масса m (кг)
— количественная мера инертности тела.

Первый закон Ньютона
:

Существуют такие системы отсчета, в которых тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют другие тела.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными
.

Сила
(Н
) — векторная величина, характеризующая взаимодействие между телами или частями тела.

Принцип суперпозиции сил
:

Если на материальную точку действуют одновременно силы и , то их можно заменить равнодействующей силой .

Примеры задач с решением

Пример 1

Задание.
Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $\frac{Н}{м}.\ $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

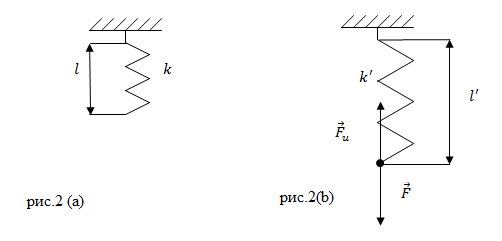
Решение.
Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:

При упругих деформациях выполняется закон Гука:

Из (1.2) найдем удлинение пружины:

\

Длина растянутой пружины равна:

Вычислим новую длину пружины:

Ответ.
1) $k»=10\ \frac{Н}{м}$; 2) $l»=0,21$ м

Пример 2

Задание.
Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $\Delta l_2$?

Решение.
Если пружины соединены последовательно, то деформирующая сила ($\overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:

Для второй пружины запишем:

Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:

Из равенства (2.3) получим удлинение первой пружины:

\

Ответ.
$\Delta l_1=\frac{k_2\Delta l_2}{k_1}$

Мы уже неоднократно пользовались динамометром – прибором для измерения сил. Познакомимся теперь с законом, позволяющим измерять силы динамометром и обуславливающим равномерность его шкалы.

Известно, что под действием сил возникает деформация тел
– изменение их формы и/или размеров
. Например, из пластилина или глины можно вылепить предмет, форма и размеры которого будут сохраняться и после того, когда мы уберём руки. Такую деформацию называют пластической. Однако, если наши руки деформируют пружину, то когда мы их уберём, возможны два варианта: пружина полностью восстановит форму и размеры или же пружина сохранит остаточную деформацию.

Если тело восстанавливает форму и/или размеры, которые были до деформации, то деформация упругая
.
Возникающая при этом в теле сила – это сила упругости, подчиняющаяся закону Гука
:

Поскольку удлинение тела входит в закон Гука по модулю, этот закон будет справедлив не только при растяжении, но и при сжатии тел.

Опыты показывают: если удлинение тела мало по сравнению с его длиной, то деформация всегда упругая;
если удлинение тела велико по сравнению с его длиной, то деформация, как правило, будет пластической
или даже разрушающей
. Однако, некоторые тела, например, резинки и пружины деформируются упруго даже при значительных изменениях их длины. На рисунке показано более чем двухкратное удлинение пружины динамометра.

Для выяснения физического смысла коэффициента жёсткости, выразим его из формулы закона. Получим отношение модуля силы упругости к модулю удлинения тела. Вспомним: любое отношение показывает, сколько единиц величины числителя приходится на единицу величины знаменателя. Поэтому коэффициент жёсткости показывает силу, возникающую в упруго деформированном теле при изменении его длины на 1 м.

1. Динамометр является…
2. Благодаря закону Гука в динамометре наблюдается…
3. Явлением деформации тел называют…
4. Пластически деформированным мы назовём тело, …
5. В зависимости от модуля и/или направления приложенной к пружине силы, …
6. Деформацию называют упругой и считают подчиняющейся закону Гука, …
7. Закон Гука носит скалярный характер, так как с его помощью можно определить только…
8. Закон Гука справедлив не только при растяжении, но и при сжатии тел, …
9. Наблюдения и опыты по деформации различных тел показывают, что…
10. Ещё со времени детских игр мы хорошо знаем, что…
11. По сравнению с нулевым штрихом шкалы, то есть недеформированным начальным состоянием, справа…
12. Чтобы понять физический смысл коэффициента жёсткости, …
13. В результате выражения величины «k» мы…
14. Ещё из математики начальной школы мы знаем, что…
15. Физический смысл коэффициента жёсткости состоит в том, что он…

Не зная, чему равна сила растяжения пружины, невозможно вычислить коэффициент ее жесткости, поэтому найдите силу растяжения. То есть, Fупр = kx , где k и является коэффициентом жесткости. В этом случае вес груза будет равен силе упругости, действующей на тело, коэффициент жесткости которого нужно найти, например, пружины.

При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается. Физика 7 класс, тема 03. Силы вокруг нас (13+2 ч) Сила и динамометр. Виды сил. Уравновешенные силы и равнодействующая. Физика 7 класс, тема 06. Введение в термодинамику (15+2 ч) Температура и термометры.

Особенности расчета жесткости соединений пружин

Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.

При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.

При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.

Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.

Опытный метод

Чтобы понять, как найти жесткость пружины, а точнее, определить коэффициент жесткости пружины опытным путем, следует произвести следующие манипуляции. Вам необходимо деформировать тело, прилагая к нему силу. Самый простой вид деформации – это сжатие или растяжение. Коэффициент жесткости показывает именно то, какую силу необходимо приложить к телу, чтобы упруго деформировать его на единицу длины. Мы сейчас говорим об упругой деформации, когда тело принимает свою первоначальную форму после совершения воздействия на него. Для того чтобы провести этот наглядный эксперимент вам потребуются следующие вещи:

• калькулятор,
• ручка,
• тетрадь,
• пружина,
• линейка,
• груз.

Итак, один конец пружины закрепите вертикально, а второй оставьте свободным. Измерьте длину пружины и запишите результат в тетрадь (это будет значение x1). Подвесьте к свободному концу пружины груз весом в сто граммов и опять измерьте длину пружины, запишите значение (x2). Рассчитайте абсолютное удлинение пружины (разница значений x1 и x2). При небольших сжатиях и растяжениях сила упругости пропорциональна деформации. Здесь уже применяем Закон Гука, согласно которому Fупр = |kx|, где k и является коэффициентом жесткости. Для того чтобы найти нужный нам коэффициент жесткости надо силу растяжения разделить на удлинение пружины. Силу растяжения находим следующим образом: Fупр = — N = -mg. Отсюда следует, что mg = kx. А значит, k = mg/x. Дальше все просто: подставьте известные вам значения в формулу и найдите, чему равна жёсткость пружины.

Определение

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости
.

Чаще всего ее обозначают ${\overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

Рассмотрим пружину, на которую действует растягивающая сила ($\overline{F}$), которая направлена вертикально вниз (рис.1).

Силу $\overline{F\ }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${\overline{F}}_u$), уравновешивающая силу $\overline{F\ }$. Если деформация является небольшой и упругой, то удлинение пружины ($\Delta l$) прямо пропорционально деформирующей силе:

\

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

\=\frac{\left}{\left}=\frac{Н}{м}.\]

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.

Коэффициент жесткости цилиндрической пружины

На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:

1. При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
2. При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
3. Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
4. Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.

Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:

1. Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
2. Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
3. Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.

Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:

1. Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
2. Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
3. Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
4. Модуля сдвига, который зависит от типа применяемого материала.

Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.