Что такое аксиома

Основные понятия стереометрии

Стереометрия оперирует всеми теми понятиями, которые нам известны из планиметрии – точка, прямая, окружность, треугольник и т. д. Но помимо них добавляются и иные термины.

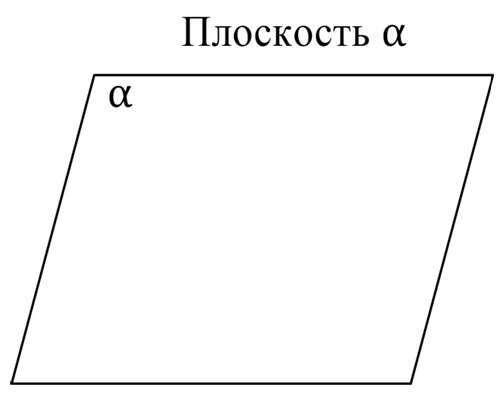
Важнейшее из основных понятий стереометрии – это плоскость. Иногда в литературе применяется сокращение плос-ть. Строгого определения плоскости в рамках геометрии не дают, это понятие считается исходным, как понятия точки или прямой в планиметрии. Лишь некоторые ее свойства косвенно указываются с помощью аксиом. В реальной жизни примерами плоскости являются поверхность стола или лист бумаги. Однако, в отличие от них, плоскость не имеет границы, она бесконечна (как и прямая). Плоскость не имеет кривизны, поэтому, например, поверхность шара плоскостью не является. При изображении плоскости на чертежах ее обычно показывают в виде параллелограмма, при этом традиционно их обозначают маленькими буквами греческого алфавита, которые в планиметрии используются для обозначения углов (α, β, γ и т. п. ):

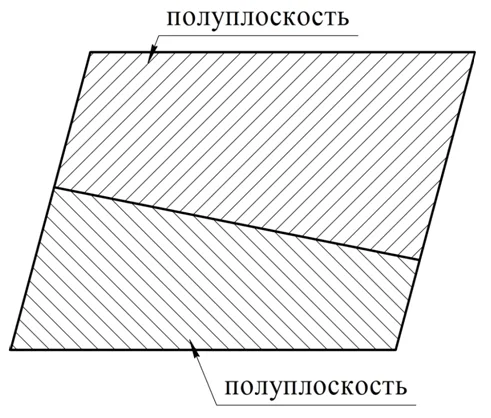
Если на плоскости проведена прямая, то она разобьет ее на две фигуры, которые именуются полуплоскостями:

Объемные фигуры – это часть пространства, которая отделена от остального пространства замкнутой поверхностью, то есть границей. Простейший пример объемной фигуры – это куб:

Поверхность куба – это 6 равных квадратов, каждый из них именуется гранью куба. Стороны этих квадратов – это уже ребра куба, а вершины квадратов одновременно являются и вершинами кубов.

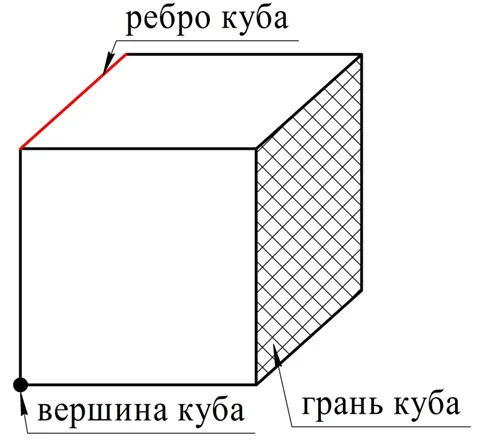
Обратите внимание на изображение куба. Здесь он показан немного сбоку, в результате чего изображение становится объемным

Однако при этом мы вынуждены искажать некоторые размеры и углы на чертеже. Например, верхняя грань должна быть квадратом, но на плоском рисунке углы у этой грани прямыми не являются. При необходимости мы просто ставим специальный значок перпендикулярности между отрезками, который использовали и в планиметрии:

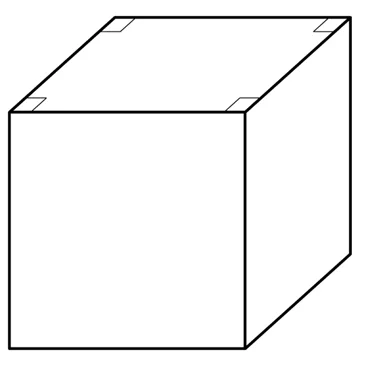
Важно понимать, что из-за искажения размеров у объемных фигур на плоских чертежах мы НЕ можем проверить решение некоторых стереометрических задач с помощью точных построений. Однако есть специальные компьютерные программы 3-D черчения, в которых такие построения уже можно выполнить

Также заметим, что на рисунке видны не все 6 граней куба, а только 3 из них. Если возникает необходимость показать невидимые на чертеже линии, то использует штриховые линии:

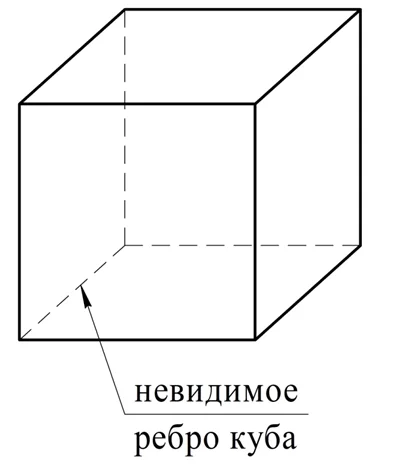
Все грани куба – это многоугольники. Если у фигуры вся ее поверхность состоит лишь из многоугольников, то она именуется многогранником. Таким образом, куб является примером многогранника. Другими примерами многогранников могут служить параллелепипед, пирамида, усеченная пирамида:

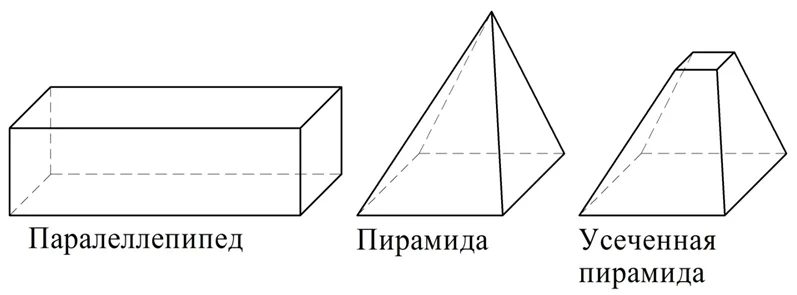
Более подробно различные виды многогранников будут рассматриваться позднее, тогда же им будут даны и их определения.

Если у объемной фигуры хоть одна поверхность не является многоугольником, то она не может считаться многогранником. Наиболее простыми и часто встречающимися такими фигурами являются шар, цилиндр, конус

Обратите внимание, что у них могут отсутствовать ребра и вершины, которые обязательно есть у многогранника:

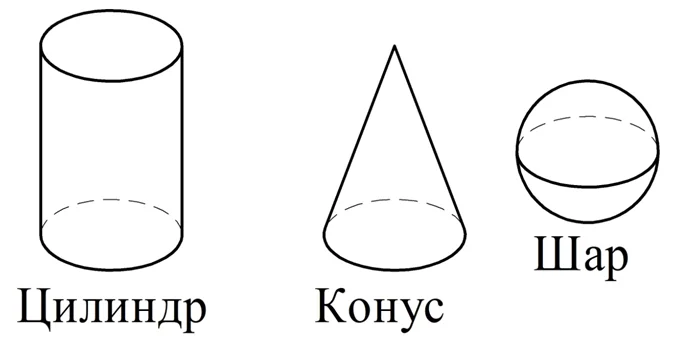
Следует различать саму объемную фигуру и ее границу. Так, шар – это объемная фигура, а поверхность шара – это сфера.

Вторая теорема о неполноте

Вторая теорема Гёделя о неполноте, которая доказывается путем формализации части доказательства первой теоремы внутри самой системы, утверждает, что:

Пусть Т — достаточно выразительная математическая теория, чтобы содержать арифметику: если Т непротиворечива , невозможно доказать непротиворечивость Т внутри Т.

С некоторым упрощением,

Никакая система, которая является связной и достаточно выразительной, чтобы содержать арифметику, не может быть использована для демонстрации собственной связности.

Этот результат оказал разрушительное воздействие на философский подход к математике, известный как программа Гильберта . Дэвид Гильберт считал, что согласованность сложных формальных систем, таких как система математического анализа в области действительных чисел , может быть продемонстрирована путем разбиения системы на более простые системы. Таким образом, проблема согласованности всей математики могла бы быть прослежена до согласованности элементарной арифметики. Вторая теорема Гёделя о неполноте показывает, что, поскольку даже такая простая система, как система элементарной арифметики, не может быть использована для доказательства ее собственной связности, тем более ее нельзя использовать для доказательства связности более мощных систем.

Примеры Аксиоматических теорий

Рассмотрим концепции, развитые обоими вариантами:

Теория конгруэнтности расстояний. Есть R множество расстояний и ≅ отношение, называемое коэффициентом конгруэнтности, таким образом, что выражение c ≅ k обозначает следующее: расстояние c конгруэнтно расстоянию k. Как аксиомы приняты эти положения:

E1. Для любого c из R c ≅ c. E2. Для любых элементов c, k, t из R, если c ≅ t и k ≅ t, то c ≅ k Теорема: Для произвольных компонентов c и t из R, если k ≅ t, то t ≅ k Док-во: В соответствии с аксиомой E2, заменив t на c, получим, что если t ≅ t и k ≅ t, то t ≅ k. Поскольку член конъюнкции t ≅ t истинен (E1), то из конъюнкции его исключим и получим, что t ≅ k.

Теория о натуральных числах, созданная Д. Пеано. Построена на определениях непустого множества E, бинарного отношения «‘», а также выделенного элемента «1». В ней выбраны такие аксиомы: (K1) (∀ c) (c’ ≠ 1); (K2) (∀ c, t) (c = t → c’ = t’); (K3) (∀ c, t) (c’ = t’ → c = t); (K4) (1∈S ^ (∀ c (c∈S→ c’∈S)) →S=R.

Ниже приведено доказательство теоремы, выведенной из вышеперечисленных аксиом.

(∀ с) (с’ ≠ с)

Док-во: Рассматриваем совокупность T = {c ∈ R: c’ ≠ c }. Воспользуемся последней из аксиом (K4):

• 1 ∈ T, ведь 1’≠ 1 по аксиоме K1;
• Пускай, c ∈ T, иными словами. с’ ≠ с. В таком случае, согласно третей из аксиом, (c’) ‘ ≠ c’. Откуда с’ ∈ T

Четвертая аксиома соблюдена, поэтому T=R (K4), что в свою очередь означает, что (∀ с) (с’ ≠ с). Теорема доказана.

Выстраивание теории о множествах Кантора, с опорой на ряд аксиоматических систем. В сумме рассматриваются 2 системы.

Базовые определения теории K – двойные функции (∩, ∪), единичная «‘», нульарные (0 и 1). Аксиоматическая система такой теории является симметричной относительно четырех видов операций: ∩, ∪, 0, 1.

(K1) c ∩ t = t ∩ c. (K2) c ∪ t = t ∪ c. (K3) c ∩ (t ∪ e) = (c ∩ t) ∪ (c ∩ e). (K4) c ∪ (t ∩ e) = (c ∪ t) ∩ (c ∪ e). (K5) c ∩ 1 = c. (K6) c ∪ 0 = c. (K7) c ∩ c’ = 0. (K8) c ∪ c’ = 1.

Начальные определения теории номер 2 – двойная операция ∩ и унарная операция ‘. Система аксиом этой теории, напротив, является ассиметричной, она «сдвинута» к операции ∩.

(L1) c ∩ t = t ∩ c. (L2) (c ∩ t) ∩ e = c ∩ (t ∩ e). (L3) c ∩ t’ = e ∩ ez’ ⇒ c ∩ t = c. (L4) c ∩ t = c ⇒ c ∩ t’ = e ∩ e’.

Значение слова «аксиома» в словарях русского языка

Аксиома это:

Аксио́ма ( «утверждение, положение») или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами.

Википедия

Аксиома

ж. 1. Положение какой-либо научной теории, принимаемое без доказательств в силу непосредственной убедительности. 2. Неоспоримая, бесспорная, не требующая доказательств истина.

Большой современный толковый словарь русского языка

Аксиома

(гр. axioma) 1) отправное, исходное положение какой-л. теории, лежащее в основе доказательств других положений этой теории, в пределах которой оно принимается без доказательства; 2) перен. бесспорная, не требующая доказательств истина.

Новый словарь иностранных слов

Аксиома

ж. 1) Исходное положение какой-л. научной теории, принимаемое без доказательств. 2) перен. Неоспоримое, бесспорное положение, очевидная истина, не требующая доказательств.

Новый толково-словообразовательный словарь русского языка Ефремовой

Аксиома

жен. , греч. очевидность, ясная по себе и бесспорная истина, не требующая доказательств, напр. целое всегда, больше части своей; основная истина, самоистина, ясноистина.

Словарь Даля

Аксиома

1. отправное, исходное положение какой-л. теории, лежащее в основе доказательств других положений этой теории, в пределах которой оно принимается без доказательства; 2. * бесспорная, не требующая доказательств истина.

Словарь иностранных выражений

Аксиома

положение, принимаемое без доказательств Lib аксиома исходное положение, принимаемое без доказательств и лежащее в основе доказательств истинности других положений Spec

Словарь русского языка Ожегова

Аксиома

(греч. axioma), положение, принимаемое без логического доказательства в силу непосредственной убедительности; истинное исходное положение теории.

Современный толковый словарь, БСЭ

Аксиома

аксиома ж. 1) Исходное положение какой-л. научной теории, принимаемое без доказательств. 2) перен. Неоспоримое, бесспорное положение, очевидная истина, не требующая доказательств.

Толковый словарь Ефремовой

Аксиома

аксиомы, ж. (греч. axioma). Положение, принимаемое без доказательств (мат.). || Очевидная истина, утверждение, принимаемое на веру (книжн.).

Толковый словарь русского языка Ушакова

ОСНОВАНИЕ в логике Гегеля[]

    Для справки:   Терминология Диалектической ЛОГИКИ.

Оттолкнувшись от системы аксиом классической ФЛ, Гегель сформулировал свою систему принципов, но сделал он это не явно, по умолчанию:

1) Принцип ОСНОВАНИЯ: «Любое УМОЗАКЛЮЧЕНИЕ должно иметь своё ОСНОВАНИЕ«.

Гегель Лейбницевское определение ОСНОВАНИЯ как «достаточного» посчитал совершенно излишним, справедливо полагая: что же это за ОСНОВАНИЕ и может ли оно таковым быть, если его НЕ достаточно для УМОЗАКЛЮЧЕНИЯ! (Смотри «Наука логики», т.2, Учение о сущности, Глава третья. Основание.)

С другой стороны, если ОСНОВАНИЕ не является достаточным для проведения УМОЗАКЛЮЧЕНИЯ, то у УМОЗАКЛЮЧЕНИЯ вообще нет никакого ОСНОВАНИЯ.

По умолчанию и Гегель и Маркс считали ОСНОВАНИЕМ логического вывода не СУЖДЕНИЕ (или совокупность суждений, как в формальной логике), а ПОНЯТИЕ (!).

Назначение[править | править код]

Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и, если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.

В современной науке вопрос об истинности аксиом, лежащих в основе какой-либо теории, решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.

Аксиоматиза́ция (или — формализация) теории — явное указание конечного или счётного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, всё дальнейшее изложение должно основываться исключительно на этих аксиомах и не опираться на обычное конкретное значение этих объектов и их отношений.

Выбор аксиом, которые составляют основу конкретной теории, не является единственным. Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и евклидовой геометрии.

Набор аксиом называется непротиворечивым, если исходя из аксиом данного набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание.

Австрийский математик Курт Гёдель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система), в которой можно определить натуральные числа, сложение и умножение, неполна. Это значит, что найдётся бесконечное количество математических утверждений (функций, выражений), ни истинность, ни ложность которых не сможет быть доказана на основании данной системы аксиом. Также, по теореме о неполноте, среди этих невыводимых утверждений будет утверждение о непротиворечивости этой системы.

Развитие математического знания на основе аксиом

Когда начала развиваться новая система геометрии, изменился и аксиоматический метод. В математике стали чаще обращаться к чисто дедуктивному построению теории. В результате в современной числовой логике возникла целая система доказательств, которая является главным разделом всей науки. В математической структуре стали понимать необходимость обоснования.

Так, уже к концу столетия сформировались четкие задачи и построение сложных понятий, которые из сложной теоремы сводились к простейшему логическому утверждению. Таким образом, неевклидовая геометрия стимулировала прочную основу для дальнейшего существования аксиоматического метода, а также для решения проблем общего характера математических конструкций:

• непротиворечивости;
• полноты;
• независимости.

В процессе появился и успешно получил развитие способ интерпретации. Этот метод описывается так: для каждого выходного понятия в теории поставлен математический объект, совокупность которых называется полем. Высказывание об указанных элементах может быть ложным или истинным. В результате утверждения получают названия в зависимости от выводов.

Связь первой аксиомы с математикой

Первая аксиома является одной из фундаментальных концепций в математике. Она формулируется как «если две математические конструкции идентичны третьей, то они идентичны друг другу». Эта аксиома относится к отношению равенства и используется для доказательства различных математических утверждений.

Первая аксиома может быть применена во многих областях математики, включая алгебру, геометрию, теорию множеств и математическую логику. Она помогает установить равенство между различными объектами и определить их свойства и отношения.

Например, в алгебре первая аксиома может быть использована для доказательства равенства значений выражений или уравнений. Если два математических выражения приводят к одному и тому же результату, то они могут считаться равными по первой аксиоме.

В геометрии первая аксиома может быть использована для доказательства равенства геометрических фигур. Если две фигуры совпадают, то они равны по первой аксиоме и их свойства могут быть считаться одинаковыми.

Важно отметить, что первая аксиома служит основой для построения более сложных математических теорий и доказательств. Она помогает устанавливать равенства и определить эквивалентные свойства, что является ключевым элементом в обосновании математических утверждений

Понятие аксиомы

Аксиома – это основное предложение, которое считается истинным и не требует доказательства в рамках данной теории или системы.

Аксиома является основой для выведения других утверждений и следствий в рамках данной теории или системы. Она может быть принята на веру, постулирована, или выведена из других аксиом или предыдущих утверждений.

В математике аксиомы используются для построения формальных систем, которые позволяют анализировать и выводить новые утверждения. Некоторые известные аксиоматические теории включают аксиомы Пеано для арифметики, аксиомы геометрии Евклида и аксиомы теории множеств.

Примеры аксиом:

• Аксиома равенства в математике: если два объекта равны одному и тому же третьему объекту, то они равны друг другу.
• Аксиома выбора в теории множеств: для любой коллекции непустых множеств существует функция выбора, которая выбирает ровно один элемент из каждого множества.
• Аксиома неразрывности в физике: в пространстве нет разрывов или дыр.

Аксиомы играют важную роль в формализации знаний и построении логических и математических теорий. Они определяют базисные утверждения, от которых можно строить более сложные выводы и теории.

Решение задач

Аксиомы стереометрии часто применяются в доказательствах. И ещё в задачах с открытыми вопросами. Вот пример такой задачи:

Задача 1. Окружность и плоскость

Решение. Легко заметить, что ответ зависит от взаимного расположения точек $M$, $N$ и $O$.

Допустим, что все они лежат на одной прямой. Тогда $MN$ — диаметр, и вся окружность может как лежать в плоскости $\alpha $, так и не лежать в ней. Вот пример когда окружность не лежит в плоскости:

Пусть теперь точки $M$, $N$ и $O$ не лежат на одно прямой. По Аксиоме плоскости (Аксиома 4 в нашем списке) эти точки однозначно задают плоскость. Эта плоскость совпадает с плоскостью $\alpha $.

А поскольку окружность — плоская фигура, то остальные её точки также принадлежат плоскости $\alpha $:

Задача 2. Неравильный рисунок

Решение. Соединим точки $M$ и $K$ прямой $l$:

Мы видим, что точка $B\notin l$. Поэтому точки $M$, $B$, $K$ не лежат на одной прямой. И согласно Аксиоме плоскости (Аксиома 4 в нашем списке), эти точки однозначно задают плоскость.

С одной стороны, мы видим по рисунку, что это плоскость $\alpha $. С другой стороны, параллелограмм — плоская фигура, поэтому точки $M$, $B$, $K$ лежат ещё и в плоскости параллелограмма. А это значит, что плоскости $\alpha $ и $ABCD$ должны совпадать, чего на рисунке не происходит.

Есть и другой способ показать, что рисунок некорректен. По условию задачи, точки $M$, $B$, $K$ являются общими для плоскости $\alpha $ и плоскости $ABCD$. Согласно Аксиоме пересечения плоскостей (Аксиома 5 в нашем списке), все эти точки должны лежать на одной прямой.

Однако простое построение показывает, что точки $M$, $B$, $K$ не лежат на одной прямой, что противоречит аксиоме. Такое противоречие как раз и доказывает некорректность чертежа.

Далее мы будем лишь называть аксиомы — без нумерации.

Задача 3. Прямые на плоскости

Решение. Нарисуем прямые $a$, $b$, $c$ и обозначим их точки пересечения $M$, $N$, $K$:

Точки $M$, $N$, $K$ не лежат на одной прямой. По основной Аксиоме плоскости, эти три точки однозначно определяют некоторую плоскость $\alpha $.

Далее заметим, например, что точки $M\in \alpha $ и $N\in \alpha $ по построению. По основной Аксиоме прямой и плоскости вся прямая $MN=b$ лежит в этой плоскости, т.е. $b\subset \alpha $.

Аналогично доказывается, что прямые $a\subset \alpha $ и $b\subset \alpha $.

Задача 4. Пересечение плоскостей

Решение. Обозначим прямую, по которой пересекаются плоскости $\alpha $ и $\beta $, буквой $l$:

\

Дополнительное построение: прямая $AB$, которая пересекает прямую $l$ в точке $M$:

Точки $A\in \alpha $, $B\in \alpha $. По основной Аксиоме прямой и плоскости прямая $AB\subset \alpha $ — искомая линия сечения плоскости $\alpha $ и $ABC$.

Далее заметим, что точка $M\in l\subset \beta $. Дополнительное построение: прямая $CM$:

Точки $C\subset \beta $, $M\subset \beta $. И вновь по основной Аксиоме прямой и плоскости прямая $CM$ — искомая линия сечения плоскости $\beta $ и $ABC$.

Хочу отметить, что задачи на построение — это отдельный класс задач. Как в планиметрии, так и в стереометрии. Там много интересных моментов, им посвящены отдельные уроки. А то, что мы сделали сейчас — это совсем уж простые рассуждения, которые тем не менее опираются на всю мощь аксиом.

Задача 5. Стандартное доказательство

Решение. Это классическая задача на доказательство, которую в разных формулировках предлагают во всех учебниках по стереометрии.

Обозначим параллелограмм $ABCD$. Пусть $O$ — точка пересечения диагоналей.

Поскольку точка $O\notin AB$, точки $A$, $B$, $O$ не лежат на одной прямой. По основной Аксиоме плоскости эти три точки однозначно определяют плоскость. Обозначим эту плоскость $\alpha $.

Точки $A\in \alpha $, $O\in \alpha $. По основной Аксиоме прямой и плоскости, прямая $AO\subset \alpha $. Но точка $C\in AO\subset \alpha $. Следовательно, вершина параллелограмма $C\in \alpha $. Аналогично через точки $B$ и $O$ доказывается, что вершина $D\in \alpha $.

Замечание по поводу задач

Как видите, мы рассмотрели лишь самые простые задачи

Но даже на их примере видно, насколько важно чётко знать систему аксиом

Бесчисленное множество контрольных и экзаменов были завалены просто потому, что ученик не смог обосновать простые и наглядные рассуждения. Потому что, например, не знал: можно ли утверждать, что если две точки прямой лежат на плоскости, то и вся прямая лежит на этой плоскости.

В общем, учите аксиомы и практикуйтесь на простых примерах. А для более интересных задач нам потребуются некоторые следствия из этих аксиом. Чему и посвящён следующий урок.:)

1. Следствия из аксиом стереометрии
2. Теорема о трёх перпендикулярах
3. Комментарий к пробному ЕГЭ от 7 декабря
4. Метод Гаусса
5. Задачи про температуру и энергию звезд
6. Задача B4 про шерсть и свитер

Аксиоматический метод и его структура

Забавно, но аксиоматический метод упрощенно можно представить в виде фамильного древа. Рассмотрим его схематику: за точку «отсчета» берется набор аксиом, на основе которых далее формируются предположения. Если истинность предположения подтверждается путем доказательства, оно становится теоремой.

Примечание. Знание каких-либо аксиом или теорем на данном этапе совершенно необязательно. Ваша основная задача — просто понять, как связаны все эти элементы схемы выше. Далее мы этим и займемся.

Доказательство в геометрии — важный «связующий мостик» между предпосылками и подтвержденными утверждениями. Вообще, аксиоматический метод задает бесконечный маршрут: путь «от одного к другому» можно проделывать нескончаемо долго, используя ранее доказанные теоремы в качестве фундамента для формирования новых предположений и теорем.

Что такое аксиома?

А теперь о вкусном, и у нас, друзья, неприятность: из холодильника пропал торт. Предположим, ваша задача — доказать, что не совсем-то он и пропал. Его просто кто-то съел. Ваш внутренний Шерлок включается в игру, и вы пытаетесь найти «следы преступления» на кухне.

РАСКРЫВАЕМ ДЕЛОВо-первых, глаз замечает шоколадные крошки на столешнице. Из этого вы заключаете, что его однозначно разрезали. Подкрепляет выводы и факт, что в раковине лежит разделочная доска со следами шоколада. Во-вторых, в мусорном ведре обнаруживается упаковочный материал с надписью «Торт шоколадный». Отлично, дело раскрыто!

Если бы не одно но… За поиски пропавшей сладости вы взялись, совершенно не думая, существует ли торт. Вы приняли как данность положение, что ранее в холодильнике находился торт. Никто не пытался доказывать его существование.

Или отсутствие. Задача стояла объемнее — доказать, что его съели. Так что существование торта — вот что такое аксиома. Шуточно, конечно.

Формально определение следующее:

Аксиома в составе «цепи»

Допустим, из утверждения $A$ вы доказываете утверждение $B$. Далее из $B$ вы заключаете истинность $C$. После, из $C$ выводите утверждение $D$, и так далее.

Если расположить данное следствие утверждений друг за другом, то получается, что аксиоматический метод — это цепь. Одно цепляется за другое. Однако до бесконечности идти в обратную сторону цепочки уже не получится — у цепной ветви должно быть начало, которое уже ни к чему не прикрепляется.  

{"questions":[{"content":"В цепочке выше — $A\\Rightarrow{B}\\Rightarrow{C}\\Rightarrow{D}$ — какое из утверждений будет считаться аксиомой? `choice-1`","widgets":{"choice-1":{"type":"choice","options":,"explanations":,"answer":}}}]}

Что такое теорема?

Теперь, когда мы условились, что такое аксиома (иными словами, приняли за истину ряд положений бездоказательно), у нас сформировался каркас, на основе которого можно строить дальше. Рассмотрим еще один, чуть более разветвленный граф, где будет наглядно показано, что такое теорема и как она связывается с аксиомой.

Структурно геометрию можно представить в виде подобного графа. Он, правда, будет гораздо сложнее в устройстве, если на нем расположить все теоремы.

К примеру, рассмотрим узел $H$. Для того, чтобы туда попасть, справа необходимо пройти через узел $F$ и одну из точек старта — $С$. Слева необходим узел $D$ и точка старта $A$. Чем больше узлов, тем сложнее путь.

{"questions":[{"content":"Думаем, и так понятно, однако на всякий случай вас проверим. На графе выше, какой элемент отвечает за теорему, а какой за аксиому? `matcher-1`","widgets":{"matcher-1":{"type":"matcher","labels":,"items":}}}]}

Ребра графа, они же стрелки, — это доказательства. Начиная со «стартовых» бездоказательных утверждений (аксиом), мы выводим первые прямые следствия (теоремы) — их доказательство опирается исключительно на истинность аксиом. Далее из полученных теорем мы предполагаем существование следующих из них теорем. Доказательство нового «пакета» теорем опирается на истинность первых следствий, которые, в свою очередь, опираются на истинность принятых изначально аксиом.

Мы наконец готовы дать определение тому, что такое теорема:

Так что такое теорема? Это клубочек. Клубочек даже самой комплексно составленной теоремы можно размотать до аксиом: от последней теоремы — к другим; от них — назад к еще одной теореме, от этой теоремы — еще к ряду других, далее-далее… Ура, аксиома. Путь, который вы проделываете, заматывая клубочек, — это и есть доказательство в геометрии.

Постулат[]

Постулат (от лат. postulatum — требование), предложение (условие, допущение, правило), в силу каких-либо соображений «принимаемое» без доказательства, но, как правило, с обоснованием. (БСЭ), http://slovari.yandex.ru/dict/bse/article/00061/88500.htm?text=постулат&stpar3=1.1, или Ссылки\091005\Постулат — Яндекс.Словари.htm

Положение, принимаемое за основу в некоторой теории. В отличие от аксиомы Постулат может быть опровергнут опытом.

Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. В классическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.

Евклид был мудр, а Гейберг путался в незнакомом языке J. Ключевым является не слово «доказать», а слово «опровергнуть». Евклид понимал, что аксиома – это такое утверждение, которое в принципе невозможно опровергнуть – невозможно представить опыт, в котором не-истинность этого утверждения выявится. А постулат – это предположение, которое пока не удается опровергнуть.

Приличная физическая школа ставит эксперименты не в подтверждение, а в опровержение теории. Только неудача такого эксперимента может временно затормозить признание постулата ложным .

Аксиомы бывают только в математике и отпочковавшихся от нее науках. Т.е. только в тавтологических системах. А постулаты – в тех науках, которые апеллируют к опыту. Даже в философии нет аксиом благодаря ленинскому «практика – критерий истины»

Еще одно интересное свойство постулатов состоит в том, что, как правило, их не опровергают, а указывают границы применимости. Например, т.н. постулат относительности Галилея (в понимании не самого Галилея, а в том варианте, который приписывали Галилею его «ученички») «справедлив при скоростях много меньших скорости света».

У Галилея-то постулат относительности звучал не хуже Эйнштейновского: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. Сравните с Эйнштейном: «все физические процессы винерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения». Найдете отличия? Нет, конечно, если нужно подчеркнуть гениальность Альберта Германовича, то «специалисты» говорят, что тот указал что, мол, все относительно, а не только механика. Ну-ну… я лично считаю, что во времена Галилея просто не обращали внимания на другие законы, кроме механики J. Возрождение, однако… беспредел…

Это умники-популяризаторы изменили галилеевский принцип относительнотси на «более понятный» кинематический вариант: v’ = v +v0. Типа: скорость тела в системе отсчета 1, движущейся прямолинейно равномерно относительно системы отсчета 0, равна просто сумме скоростей тела в СО0 и относительных скоростей СО

Постулаты – это утверждения, истинность которых до сих пор не опровергнута опытом, но в принципе может быть опровергнута – а может и не быть никогда опровергнута, если постулат выражает фундаментальный закон природы. Например, истинность постулата сохранения массы (закон сохранения массы Ломоносова/Лавуазье) была опровергнута опытом, а вот закон сохранения энергии до сих пор держится

Постулат есть обобщение и абстрагирование эмпирических данных, аксиома — заявление, справедливое по объявлению

Критика первой аксиомы

Первая аксиома – это основной постулат, на котором строится математическая логика и выводятся все остальные аксиомы. Однако, вопросы и критика первой аксиомы существуют и обсуждаются уже долгое время.

1. Неясность и абстрактность:

Первая аксиома, сформулированная классическими математиками, является абстрактной и неопределенной. В ней утверждается, что «все равные друг другу суть одно и то же». Термины «все», «равные», «одно и то же» не имеют четкого и однозначного значения.

2. Исключение неуравновешенности:

Первая аксиома предполагает, что все объекты могут быть сравнимы и уравновешены друг с другом. Однако, в математике существуют неуравновешенные объекты и системы, которые не поддаются классическим методам сравнения. Это может привести к проблемам и ограничениям в применении первой аксиомы.

3. Ограничение на многомерность:

Первая аксиома предполагает существование только одного измерения и отношение равенства между объектами. Однако, в реальном мире существуют многомерные объекты и сложные системы, которые не могут быть описаны простыми равенствами. Это ограничивает применимость первой аксиомы в некоторых ситуациях.

4. Зависимость от логики:

Первая аксиома основана на математической логике и предполагает соблюдение определенных логических законов и правил. Однако, многие философы и математики отмечают, что логика может быть условной и зависеть от контекста и культурных норм. В этом случае применимость первой аксиомы может быть оспорена.

5. Критика социального значения:

Некоторые критики первой аксиомы указывают на ее социальное значение и связь с идеологическими и политическими вопросами. Они утверждают, что аксиома может быть использована, чтобы оправдать неравенство и дискриминацию на основе расы, пола или других факторов.

В итоге, первая аксиома имеет свои ограничения и спорные моменты, которые требуют дальнейшего изучения и обсуждения в контексте различных дисциплин и философских школ мысли.