Восклицательный знак перед числом: что это значит?

Различные обозначения символа

Восклицательный знак (!) в математике означает факториал числа. Однако в некоторых случаях используется двойной восклицательный знак (!!).

Двойной восклицательный знак (!!) — это оператор двойного факториала, который переходит от числа к числу, умноженному на другое число, уменьшенное на два, а затем умноженное на число, уменьшенное на четыре, и так далее.

Такое обозначение символа используется в различных областях математики, таких как комбинаторика, теория вероятностей и дифференциальные уравнения.

Двойной восклицательный знак применяется для обозначения различных комбинаторных функций, таких как числа Каталана, числа Стирлинга второго рода и числа Белла.

Пример: двойной факториал 5!! равен произведению всех нечетных чисел от 1 до 5, то есть 1 * 3 * 5 = 15.

Данный символ предоставляет удобную и компактную запись для операций, связанных с комбинаторикой, позволяя сократить количество символов при записи формул и выражений.

Использование двойного восклицательного знака в математике является одним из множества обозначений для обозначения специфических операций и функций, позволяя наглядно и кратко записывать сложные выражения.

Использование в разных областях математики

В комбинаторике двойной восклицательный знак используется для вычисления количества перестановок элементов. Например, если у нас есть набор из n элементов, то n!! показывает, сколькими способами можно переставить эти элементы.

В теории вероятностей двойной восклицательный знак используется для обозначения количества способов упорядочить набор из различных элементов или событий. Он позволяет вычислить количество перестановок без повторений.

В комбинаторной теории чисел двойной восклицательный знак часто встречается при решении задач на вычисление чисел Стирлинга. Также он используется для обозначения факториала с отрицательным аргументом, что связано с понятием гамма-функции.

Двойной восклицательный знак является важным и удобным математическим символом, обладающим множеством применений в различных областях математики.

Альтернативные символы и обозначения

Однако, существуют и другие обозначения, которые могут быть использованы вместо двойного восклицательного знака. Например, некоторые математики используют знак ‘^’ для обозначения возведения в степень, а не ‘!’. Например, для обозначения возведения числа 2 в квадрат можно использовать запись 2^2.

Также, существует особый символ для обозначения факториала — ‘n!’. Этот символ используется для обозначения факториала числа ‘n’ в математических выражениях. Например, факториал числа 10 записывается как 10!.

Универсальность символа

В математике символ двойного восклицательного знака имеет специальное значение. Он означает факториал числа. Однако, его универсальность расширяется и выходит за границы этого значения.

Символ двойного восклицательного знака, помимо своего основного значения, может использоваться в различных областях математики. Он часто используется для обозначения комбинаторных формул, в теории вероятностей, в комбинаторной математике, в численных методах и многих других областях.

В основе использования этого символа лежит его интуитивное значение — акцентирование, выделение и усиление. Восклицательный знак в математике обычно используется для обозначения факториала, что означает умножение всех натуральных чисел от 1 до данного числа

Двойной восклицательный знак, в свою очередь, подчеркивает и усиливает смысл факториала, указывая на повышенную важность этой операции в контексте задачи или формулы

Таким образом, символ двойного восклицательного знака в математике является универсальным инструментом, который помогает выразить и усилить значение различных операций и формул. Благодаря его многогранности и гибкости, он находит применение во многих областях математики и является одним из важных символов, с которыми сталкивается каждый математик.

Применение факториалов

В основе всей комбинаторики лежит .
Именно из-за него практически любая комбинаторная задача сводится к цепочке умножений.
Поэтому факториалы очень активно используются в этом разделе математики.

Последний заезд

В гранд-финале «Седалищных гонок» на креслах принимают участие 16 человек. Для них заготовили 16 «гоночных» кресел на колесиках.
Сколькими способами можно рассадить всех участников заезда на эти кресла?

На первое кресло множно усадить одного из шестнадцати гонщиков.
Вне зависимости от того, кого посадили первым, на второе кресло можно посадить одного из пятнадцати оставшихся и так далее.
По находим количество способов рассадить всех участников:

16⋅15⋅14⋅…⋅2⋅116\cdot 15\cdot 14\cdot \ldots \cdot 2\cdot 116⋅15⋅14⋅…⋅2⋅1

Мы получили цепочку умножений последовательных чисел.
Если их все перемножить, то получится большое число.
К счастью, мы уже знаем, как все это дело записать в коротком виде.
Всего существует 16! способов рассадить участников!

Проблемы Деда Мороза

Работа у Деда Мороза непростая — на Новый Год он раздает подарки хорошим детям.
Забравшись через дымоход в очередной дом Дед обнаружил внутри пятерых детишек, которые, по их заверениям, весь год вели себя хорошо.
В мешке у него 50 подарков.
Сколькими способами он может раздать подарки этим детям?

Все по новой: первому ребенку один из 50 подарков, второму один из 49 и так далее.
Нам вновь потребуется использовать и мы опять получим цепочку умножений:

50⋅49⋅48⋅47⋅4650 \cdot 49 \cdot 48 \cdot 47 \cdot 4650⋅49⋅48⋅47⋅46

Эту цепочку мы теперь тоже можем записать в коротком виде:

55‾=50!45!50^{\underline{5}} = \frac{50!}{45!}55​=45!50!​

Смысл нулевого факториала

Аналогии с комбинаторикой могут отчасти помочь разобраться и со смыслом нулевого факториала.
Представьте, что вам нужно развесить на бельевой веревке мокрую одежду: штаны, футболку и носки.
Сколькими способами это можно сделать?

Первым на веревку можно повесить любой из трех элементов одежды.
Вторым — любой из двух оставшихся, третьим только последний оставшийся элемент одежды.
Посчитаем количество способов:

3⋅2⋅1=3!=63\cdot 2\cdot 1 = 3! = 63⋅2⋅1=3!=6

Итак, всего 3! способов развесить 3 элемента мокрой одежды.
А сколько тогда есть способов развесить элементов одежды?
Только один — никаких их не развесить.

!=10! = 1!=1

Важность использования восклицательного знака

Восклицательный знак перед переменной в PHP называется оператором отрицания. Он имеет особое значение, которое заключается в изменении логического значения переменной на противоположное. Восклицательный знак позволяет выполнять определенные операции с переменными, без необходимости использования условных конструкций.

Использование восклицательного знака особенно важно в случаях, когда значение переменной может быть ложным. В такой ситуации, через оператор отрицания, можно перевести значение переменной в истинное значение

Например:

if(!$var){

echo «Переменная равна false»;

}

В данном примере, значение переменной $var равно false. Однако, используя восклицательный знак перед переменной в условии if, мы можем перевести ее значение в истинное и выполнить соответствующее действие.

Также восклицательный знак может использоваться для упрощения условных конструкций. Например:

$value = !$var ? «значение1» : «значение2»;

В данном примере, первая строка выполняет условие, когда значение переменной $var истинно, и присваивает $value значение «значение1». Вторая строка выполняет условие, когда значение переменной $var ложно, и также присваивает $value значение «значение1». В данном случае, благодаря использованию восклицательного знака, можно сократить код и выполнить одно действие вместо двух.

Таким образом, использование восклицательного знака перед переменной в PHP позволяет производить определенные операции с переменными, упрощать условные конструкции и переводить ложные значения в истинные. Это значительно упрощает работу программистов и позволяет существенно ускорить написание кода.

Преимущества использования восклицательного знака

1. Поиск ошибок в коде

Если вам нужно быстро обнаружить ошибку в коде, то применение восклицательного знака перед переменной может помочь. Если переменная не была объявлена ранее, PHP выдаст сообщение об ошибке.

2. Упрощение чтения кода

Использование восклицательного знака перед переменной позволяет улучшить читаемость кода. Когда вы видите восклицательный знак перед переменной, то сразу понимаете, что именно вы хотите сделать с этой переменной.

3. Облегчение отладки кода

Когда вы используете восклицательный знак перед переменной, PHP сообщает о любых предупреждениях и ошибках, связанных с этой переменной. Это помогает вам устранять ошибки в самом раннем этапе создания кода и повышает его надежность в будущем.

4. Защита от неожиданных значений переменных

Использование восклицательного знака перед переменной помогает защитить ваш код от возможных ошибок, если переменная содержит неожиданные значения. Если переменная содержит значение, отличное от false, 0 или пустой строки, PHP будет считать ее истинным значением.

5. Уменьшение вероятности ошибок

Использование восклицательного знака позволяет снизить вероятность ошибок, связанных с работой с неопределенными переменными. Применение восклицательного знака гарантирует, что переменная была определена, и она будет использоваться только тогда, когда это необходимо.

Выводы

Использование восклицательного знака перед переменной может улучшить качество вашего кода, сделать его менее подверженным ошибкам и обеспечить более быстрое обнаружение ошибок при их написании. Однако не рекомендуется злоупотреблять данной функцией, поскольку это может привести к более медленной работе программы и проблемам с обработкой памяти.

Недостатки использования восклицательного знака

Восклицательный знак перед переменной в PHP используется для выполнения операции отрицания. Но такое использование может иметь ряд недостатков.

• Снижение читабельности кода. Использование восклицательного знака может затруднить чтение и понимание кода, особенно для новых разработчиков, которые могут не знать всех возможных вариантов его применения.
• Непредсказуемость поведения. Если переменная перед которой стоит восклицательный знак не определена, то ее значение будет преобразовано в булево значение false. В этом случае, использование отрицания может привести к неожиданным результатам.
• Нарушение стандартов кодирования. В PHP есть определенные стандарты кодирования, которые предписывают избегать использования восклицательного знака в качестве оператора отрицания перед переменной. Нарушение этих правил может привести к трудностям при сопровождении кода и его обновлении.

В целом, использование восклицательного знака не является рекомендуемым для обычной работы с переменными в PHP. Он имеет свои недостатки и может привести к ошибкам и трудностям при разработке и сопровождении кода.

Цепочки умножений

В математике, а особенно в комбинаторике, нам регулярно приходится иметь дело с цепочками умножений последовательных чисел.
Например:

5⋅4⋅3⋅2⋅15\cdot 4\cdot 3\cdot 2\cdot 15⋅4⋅3⋅2⋅1

И в чем же проблема?
А в размере записи.
Уже в таком виде она занимает немало места.
Конечно, вместо этих умножений можно сразу записать ответ, 120, и пользоваться им.

Можно.
А что если цепочка будет длиннее?
Например, вот такой:

1⋅2⋅3⋅4⋅5⋅6⋅7⋅8⋅9⋅10⋅11⋅12⋅13⋅14⋅15⋅16⋅17⋅18⋅19⋅201\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8\cdot 9\cdot 10 \cdot 11\cdot 12\cdot 13\cdot 14\cdot 15\cdot 16\cdot 17\cdot 18\cdot 19 \cdot 201⋅2⋅3⋅4⋅5⋅6⋅7⋅8⋅9⋅10⋅11⋅12⋅13⋅14⋅15⋅16⋅17⋅18⋅19⋅20

Если все это перемножить, то получится гигантское число, которое точно также неудобно использовать:

2 432 902 008 176 640 0002 \ 432 \ 902 \ 008 \ 176\ 640 \ 0002432902008176640000

Невозможно нормально работать и выполнять операции ни с длинными цепочками умножений, ни с огромными числами в виде готового ответа.
Можно, конечно, использовать троеточие:

1⋅2⋅…⋅19⋅201\cdot 2\cdot \ldots \cdot 19 \cdot 201⋅2⋅…⋅19⋅20

Это вполне рабочий вариант, который мы будем регулярно применять. Правда, он тоже занимает довольно много места.
Вот было бы классно, если подобные цепочки умножений идущих друг раз другом чисел можно было записывать кратко и красиво…

Как избежать появления восклицательного знака возле числа?

Чтобы избежать появления восклицательного знака возле числа, вам следует учесть несколько рекомендаций:

• Избегайте использования неизвестных аббревиатур и сокращений, которые могут сбивать счет.
• Четко указывайте единицы измерения, чтобы избежать путаницы с другими значениями.
• Уточняйте контекст, в котором используется число, чтобы избежать недоразумений.
• Внимательно проверяйте правильность ввода данных, чтобы исключить возможность ошибок.
• Предоставляйте подробную информацию о числе, чтобы пользователи понимали его значение без необходимости использования восклицательного знака.
• Используйте форматирование числа в соответствии с общепринятыми стандартами, чтобы предотвратить его неправильное восприятие.

Следуя этим рекомендациям, вы сможете избежать появления восклицательного знака возле числа и обеспечить точное и понятное представление информации. Помните, что ясность и точность являются важными аспектами коммуникации, особенно когда речь идет о числах и количественных данных.

Алгебра: основные понятия и принципы

Алгебра — это раздел математики, который изучает законы и операции, связанные с символическими и числовыми объектами. Она является одной из основных областей математики и широко применяется в различных научных и инженерных дисциплинах.

В алгебре используются различные понятия и принципы, которые позволяют проводить операции и решать уравнения. Некоторые из них включают:

• Переменные: символы, которые представляют неизвестные значения. Они обычно обозначаются буквами, такими как x, y, z.
• Коэффициенты: числа, умножаемые на переменные. Например, в выражении 2x, 2 — это коэффициент.
• Выражения: математические комбинации переменных, коэффициентов и операций. Например, 3x + 2y — 5.
• Уравнения: математические выражения, содержащие знак равенства. Например, 2x + 5 = 10.
• Операции: математические операции, такие как сложение, вычитание, умножение и деление. Они применяются к выражениям для получения новых выражений.

Понимание этих основных понятий и принципов является важным для решения алгебраических задач. Например, чтобы решить уравнение, необходимо применить правила алгебры, такие как свойства операций и законы уравнений.

Также алгебра имеет свою систему символов и обозначений, среди которых наиболее распространены: восклицательный знак, который обозначает факториал числа; степень, представляющая повторное умножение числа самого на себя; квадратный корень, обозначающий число, которое возводится в квадрат, чтобы получить исходное число; и знаки сравнения, используемые для сравнения чисел.

Обозначение	Описание
!	Обозначение факториала числа. Например, 4! равно 4 * 3 * 2 * 1 = 24.
x2	Обозначение степени числа. Например, x2 означает x * x.
√x	Обозначение квадратного корня числа. Например, √25 равно 5, потому что 5 * 5 = 25.
<, >, ≤, ≥	Знаки сравнения для меньше, больше, меньше или равно и больше или равно соответственно.

Использование этих символов и обозначений позволяет записывать и решать алгебраические выражения, уравнения и неравенства в компактной и удобной форме.

Влияние на восприятие информации

Восклицательный знак рядом с цифрой может значительно влиять на восприятие информации и ее интерпретацию. Он выделяет конкретное число и придает ему особую силу и значимость в контексте сообщения.

Во-первых, восклицательный знак может указывать на уникальность, редкость или важность числа

Он может привлечь внимание читателя и создать эмоциональную реакцию, вызывая интерес и любопытство. Например, «10 фактов о счастье!», «5 секретов успешной карьеры!» или «100 рецептов идеального пирога!» — такие заголовки с восклицательным знаком сразу привлекают внимание и создают ощущение, что представленный материал является особенным и ценным

Во-вторых, восклицательный знак может дополняться словесными или визуальными выражениями, которые подчеркивают важность числа. Например, «Только сегодня! Скидка 50%!», «Ограниченное предложение! Только первым 100 клиентам!» или «Специальное предложение! Только до конца недели!» — в таких случаях восклицательный знак усиливает эффект срочности и делает предложение более привлекательным

Кроме того, восклицательный знак может использоваться для подчеркивания необычности или удивительности числа. Например, «20 фактов о животных, которые вам покажутся невероятными!» или «7 удивительных мест, которые вы должны посетить!» — в таких случаях восклицательный знак создает ощущение удивления и интереса у читателя, вызывая желание узнать больше о представленной информации.

В целом, восклицательный знак рядом с цифрой играет важную роль в оформлении и передаче информации

Он может привлечь внимание, добавить эмоциональности и значимости, а также подчеркнуть уникальность и важность числа в контексте сообщения

Начало и конец

Восклицательный знак, стоящий рядом с цифрой, может использоваться для выражения особенных значений и контекста.

Начало: Когда восклицательный знак стоит перед числом, он может указывать на начало чего-то важного или волнительного. Например, знак «1!» может означать начало новой эпохи, нового проекта или исторического события

Конец: Если восклицательный знак стоит после числа, он может указывать на окончание чего-то великого или необычного. Например, «10!» может символизировать завершение десятилетнего периода или достижение высокой отметки.

Восклицательный знак в таком контексте помогает подчеркнуть важность числа и передать сильное эмоциональное воздействие

FAQ

Зачем нужен восклицательный знак перед переменной в PHP?

Оператор восклицательного знака перед переменной используется в PHP для выполнения логической операции НЕ. В таком случае, если значение переменной равно false, то результатом будет true, а если значение переменной равно true, то результатом будет false. То есть, восклицательный знак меняет значение переменной на противоположное.

Как проверить результат выполнения оператора восклицательного знака?

Результат выполнения оператора восклицательного знака можно проверить с помощью функции var_dump(), которая выводит тип данных и значение переменной. Если значение переменной изначально было false, то после применения оператора восклицательного знака оно станет true и, соответственно, в результате выполнения функции var_dump() будет указан тип данных bool и значение true.

Какие переменные можно использовать с оператором восклицательного знака?

Оператор восклицательного знака можно использовать с переменными различных типов данных: bool, string, int, float и т.д.

Как правильно написать условие, используя оператор восклицательного знака?

Для написания условия с использованием оператора восклицательного знака необходимо указать имя переменной, перед которой будет стоять восклицательный знак, и после знака сравнения указать значение, с которым будет производиться сравнение. Например, чтобы проверить, является ли переменная $a не равной 0, нужно написать условие if (!$a == 0) { … }

Объяснение:

Формальное определение #n #! (n факториал) — произведение всех натуральных чисел, меньших или равных # П #, В математических символах:

#n! = n * (n-1) * (n-2) … #

Поверь мне, это менее запутанно, чем кажется. Скажи, что ты хотел найти #5!#, Вы просто умножаете все числа, меньшие или равные #5# пока вы не доберетесь до #1#:

#5! = 5*4*3*2*1=120#

Или же #6!#:

#6! = 6*5*4*3*2*1=720#

Самое замечательное в факториалах — это то, как легко вы можете их упростить. Допустим, вы получили следующую проблему:

вычисление #(10!)/(9!)#.

Исходя из того, что я сказал вам выше, вы можете подумать, что вам нужно будет умножить #10*9*8*7…# и разделить его на #9*8*7*6…#что, вероятно, займет много времени. Тем не менее, это не должно быть так сложно. поскольку #10! = 10*9*8*7*6*5*4*3*2*1#, а также #9! = 9*8*7*6*5*4*3*2*1#Вы можете выразить проблему следующим образом:

#(10*9*8*7*6*5*4*3*2*1)/(9*8*7*6*5*4*3*2*1)#

И посмотрите на это! Число #1# через #9# отменить:

# (10 * cancel9 * cancel8 * cancel7 * cancel6 * cancel5 * cancel4 * cancel3 * cancel2 * cancel1) / (cancel9 * cancel8 * cancel7 * cancel6 * cancel5 * cancel4 * cancel3 * cancel2 * cancel1) #

Оставив нас с #10# в результате.

Кстати, #0! = 1#, Чтобы узнать почему, проверьте эту ссылку.

Приложения Факториалов

Место, где факториалы действительно полезны, — это вероятность. Например: сколько слов вы можете сделать из букв # ABCDE #, не повторяя ни одной буквы? (Слова в этом случае не должны иметь смысла — вы можете иметь # AEDCB #, например).

Ну у вас есть #5# выбор для вашего первого письма, #4# для вашего следующего письма (помните — без повторов; если вы выбрали # A # для вашего первого письма, вы можете выбрать только # BCDE # для вашего второго), #3# для следующего, #2# для одного после этого, и #1# за последний. Правила вероятности говорят, что общее количество слов является продуктом выбора:

#underbrace (5) _ («выбор по первой букве») * 4 * 3 * 2 * 1 #

И четыре — это количество вариантов для второй буквы и так далее. Но подождите — мы узнаем это, верно! Это #5!#:

#5! = 5*4*3*2*1=120#

Так что есть #120# пути.

Вы также увидите факториалы, используемые в перестановки а также комбинации, что также связано с вероятностью. Символ для перестановок #»_энергетический ядерный реактор#и символ для комбинаций # «_ NC_r # (люди используют # ((П), (г)) # для комбинаций большую часть времени, и вы говорите «n выбирают r».) Формулы для них:

# «_ NP_r = (п!) / ((П-т)!) #

# «_ NC_r = (п!) / ((П-р)! Г!) #

Там мы видим нашего друга, факториала. Объяснение перестановок и комбинаций сделает этот длинный ответ еще длиннее, поэтому просмотрите эту ссылку для перестановок и эту ссылку для комбинаций.

Убывающий факториал

М Ã½Ã°ÃÂÃÂøûøÃÂàÃÂðñþÃÂðÃÂààÃÂõÿþÃÂúðüø ÃÂüýþöõýøù, úþÃÂþÃÂÃÂõ ýðÃÂøýðÃÂÃÂÃÂààõôøýøÃÂÃÂ.
ÃÂþ òõôàÃÂðú ñÃÂòðõàôðûõúþ ýõ òÃÂõóôð!
ÃÂðÿÃÂøüõÃÂ:

100âÂÂ99âÂÂ98âÂÂ9711âÂÂ9âÂÂ10âÂÂ7âÂÂ83âÂÂ4âÂÂ5âÂÂ6100 \cdot 99 \cdot 98 \cdot 97 \qquad 11 \cdot 9 \cdot 10 \cdot 7 \cdot 8 \qquad 3\cdot 4 \cdot 5 \cdot 6100âÂÂ99âÂÂ98âÂÂ9711âÂÂ9âÂÂ10âÂÂ7âÂÂ83âÂÂ4âÂÂ5âÂÂ6

ÃÂðú úþÃÂþÃÂúþ ÷ðÿøÃÂÃÂòðÃÂàøÃÂ?
äðúÃÂþÃÂøðû øÃÂÿþûÃÂ÷þòðÃÂàýõ ÿþûÃÂÃÂøÃÂÃÂÃÂ, ÿþÃÂþüàÃÂÃÂþ ÃÂÃÂø ÃÂõÿþÃÂúø ýõ ÃÂþôõÃÂöðàõôøýøÃÂÃÂ.
ÃÂÃÂÃÂþôøÃÂ, ÃÂÃÂþ ýøúðú…
ÃÂþÃÂþöõ, þôýþóþ ÃÂþûÃÂúþ ÃÂðúÃÂþÃÂøðûð ýðü ýõ ÃÂòðÃÂðõÃÂ.

ÃÂÃÂÃÂÃÂõÃÂðÃÂÃÂÃÂàÃÂðúøõ ýõÿþûýþÃÂõýýÃÂõ øûø ýõÿþûýÃÂõ ÃÂðúÃÂþÃÂøðûàò úþüñøýðÃÂþÃÂøúõ, ôð ø ýõ ÃÂþûÃÂúþ ò ýõù, ÃÂõóÃÂûÃÂÃÂýþ.
ÃÂûàÃÂôþñýþù ÃÂðñþÃÂààýøü ÿÃÂøôÃÂüðûø ÃÂñÃÂòðÃÂÃÂøù ÃÂðúÃÂþÃÂøðû:

àúþýÃÂõ ÃÂõÿþÃÂúø üýþöøÃÂõûàøüõõàòøô nâÂÂ(kâÂÂ1)n-(k-1)nâÂÂ(kâÂÂ1), ð ýõ nâÂÂkn-knâÂÂk, ÿþÃÂþüàÃÂÃÂþ òÃÂÃÂøÃÂðõüþõ ø÷ n ò úðöôþü üýþöøÃÂõûõ ÃÂøÃÂûþ ( ò ÿõÃÂòþü, 1 òþ òÃÂþÃÂþü, 2 ò ÃÂÃÂõÃÂÃÂõü ø ÃÂ.ô.) ýþüõÃÂð ÃÂðüþóþ üýþöøÃÂõûÃÂ.
ÃÂýðÃÂøÃÂ, ò k-ÃÂþü üýþöøÃÂõûõ ñÃÂôõàòÃÂÃÂøÃÂðÃÂÃÂÃÂàkâÂÂ1k-1kâÂÂ1.

äþÃÂüÃÂûàÃÂñÃÂòðÃÂÃÂõóþ ÃÂðúÃÂþÃÂøðûð üþöýþ ôþòþûÃÂýþ ÿÃÂþÃÂÃÂÃÂü ÃÂÿþÃÂþñþü òÃÂÃÂð÷øÃÂàÃÂõÃÂõ÷ ÃÂöõ ø÷òõÃÂÃÂýÃÂù ýðü þñÃÂÃÂýÃÂù ÃÂðúÃÂþÃÂøðû:

âõÿõÃÂÃÂ, ÷ýðàÿÃÂþ ÃÂñÃÂòðÃÂÃÂøù ÃÂðúÃÂþÃÂøðû ø õóþ ÃÂþÃÂüÃÂûÃÂ, üàüþöõü ò úþÃÂþÃÂúþù ÃÂþÃÂüõ ÷ðÿøÃÂÃÂòðÃÂàýõÿþûýÃÂõ ÃÂõÿþÃÂúø ÃÂüýþöõýøù ÿþÃÂûõôþòðÃÂõûÃÂýÃÂàÃÂøÃÂõû:

104â¾=100!96!115â¾=11!6!64â¾=6!2!100^{\underline{4}} = \frac{100!}{96!} \qquad 11^{\underline{5}} = \frac{11!}{6!} \qquad 6^{\underline{4}} = \frac{6!}{2!}104âÂÂ=96!100!âÂÂ115âÂÂ=6!11!âÂÂ64âÂÂ=2!6!âÂÂ

ÃÂÃÂûø õÃÂÃÂàÃÂñÃÂòðÃÂÃÂøù ÃÂðúÃÂþÃÂøðû, ÃÂþ ôþûöõý ñÃÂÃÂàø òþ÷ÃÂðÃÂÃÂðÃÂÃÂøù?
ÃÂý ôõùÃÂÃÂòøÃÂõûÃÂýþ ÃÂÃÂÃÂõÃÂÃÂòÃÂõÃÂ, ýþ øÃÂÿþûÃÂ÷ÃÂõÃÂÃÂàÃÂõôúþ, òõôàôþÃÂÃÂðÃÂþÃÂýþ ÃÂõÿþÃÂúàÃÂüýþöõýøù ÿÃÂþÃÂøÃÂðÃÂàøûø ÷ðÿøÃÂðÃÂàò þñÃÂðÃÂýþü ÿþÃÂÃÂôúõ ø òþ÷ÃÂðÃÂÃÂðÃÂÃÂøù ÃÂðúÃÂþÃÂøðû ÿÃÂõòÃÂðÃÂøÃÂÃÂàò ÃÂñÃÂòðÃÂÃÂøù.
ÃÂþ ýõ òþûýÃÂùÃÂõÃÂÃÂ, ò ÿÃÂðúÃÂøúÃÂüõ…

Какие свойства и формулы есть у факториалов

Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:

• Факториал нуля равен единице — 0! = 1.
• Факториал единицы тоже равен единице: 1! = 1.
• Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.

Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.

Формула Стирлинга

Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:

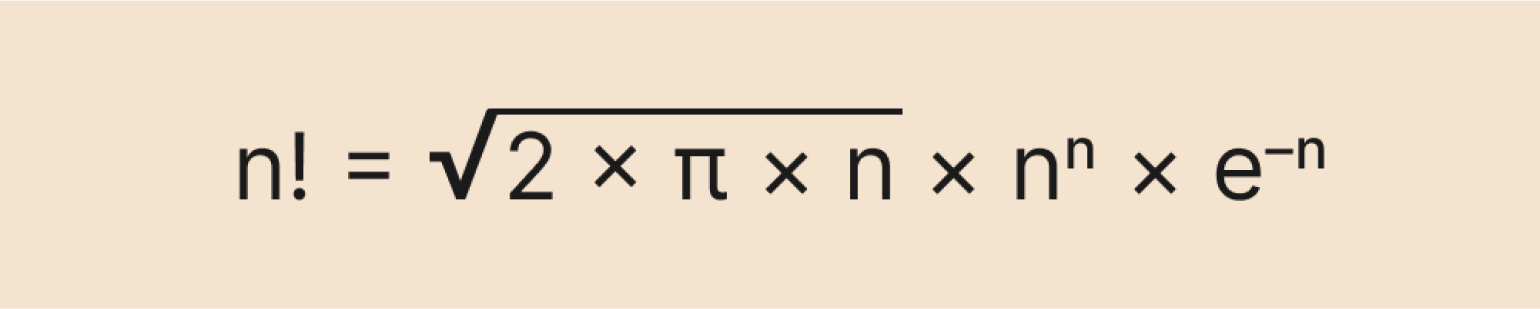
Изображение: Skillbox Media

Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).

Онлайн-калькулятор не справился с вычислением такого большого числа, как факториал 10 024Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media

Давайте попробуем вычислить факториал числа 6 по этой формуле:

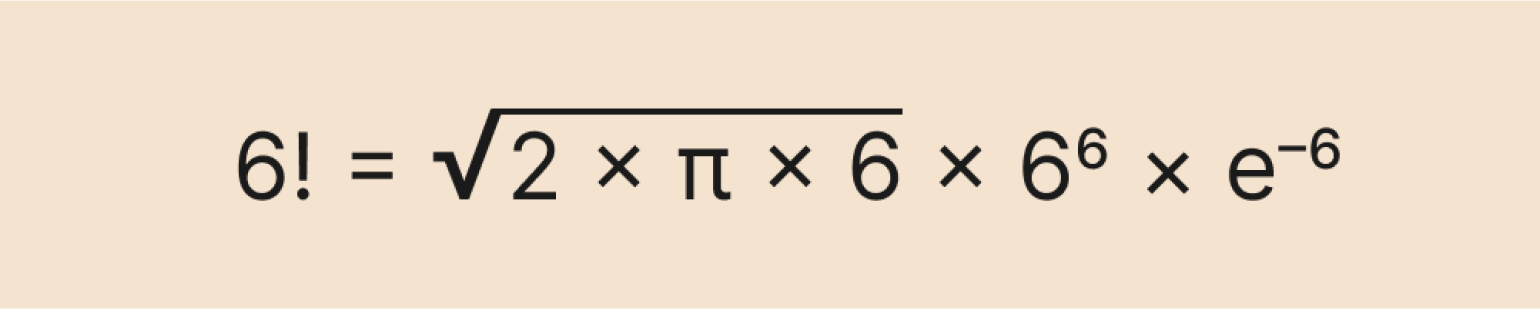
Изображение: Skillbox Media

Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:

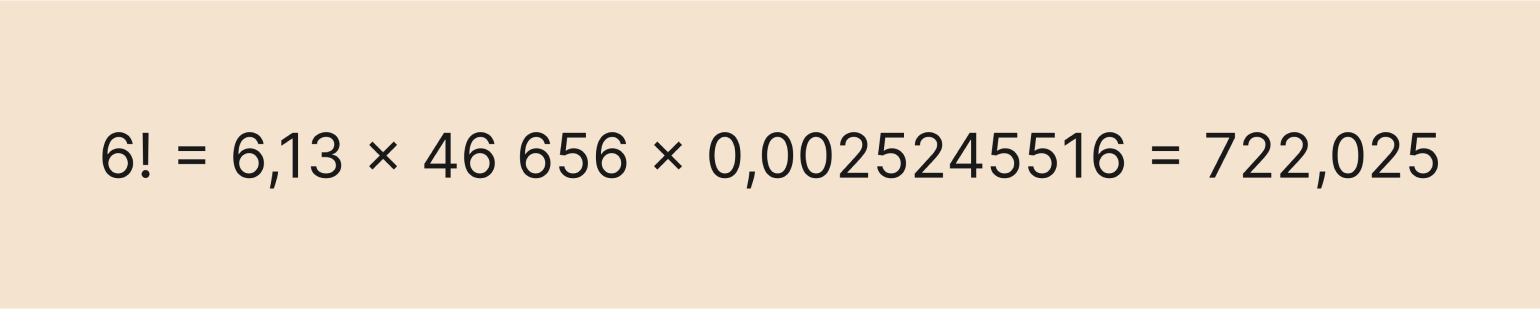
Изображение: Skillbox Media

Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:

Изображение: Skillbox Media

Это уже больше похоже на правду. Хотя погрешность всё равно есть.

Рекуррентная формула

Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:

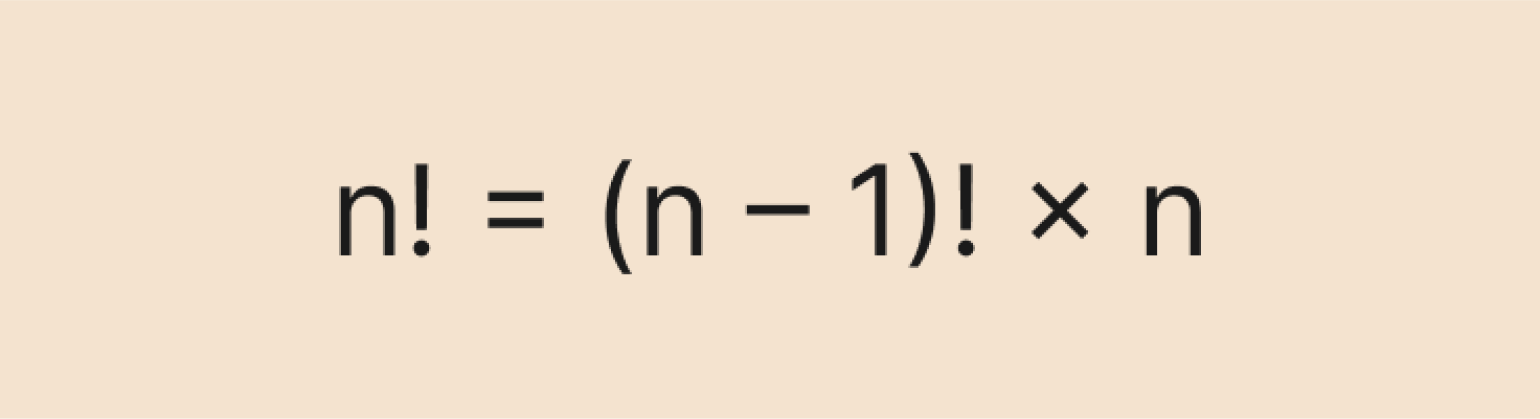
Изображение: Skillbox Media

В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.

Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.

Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:

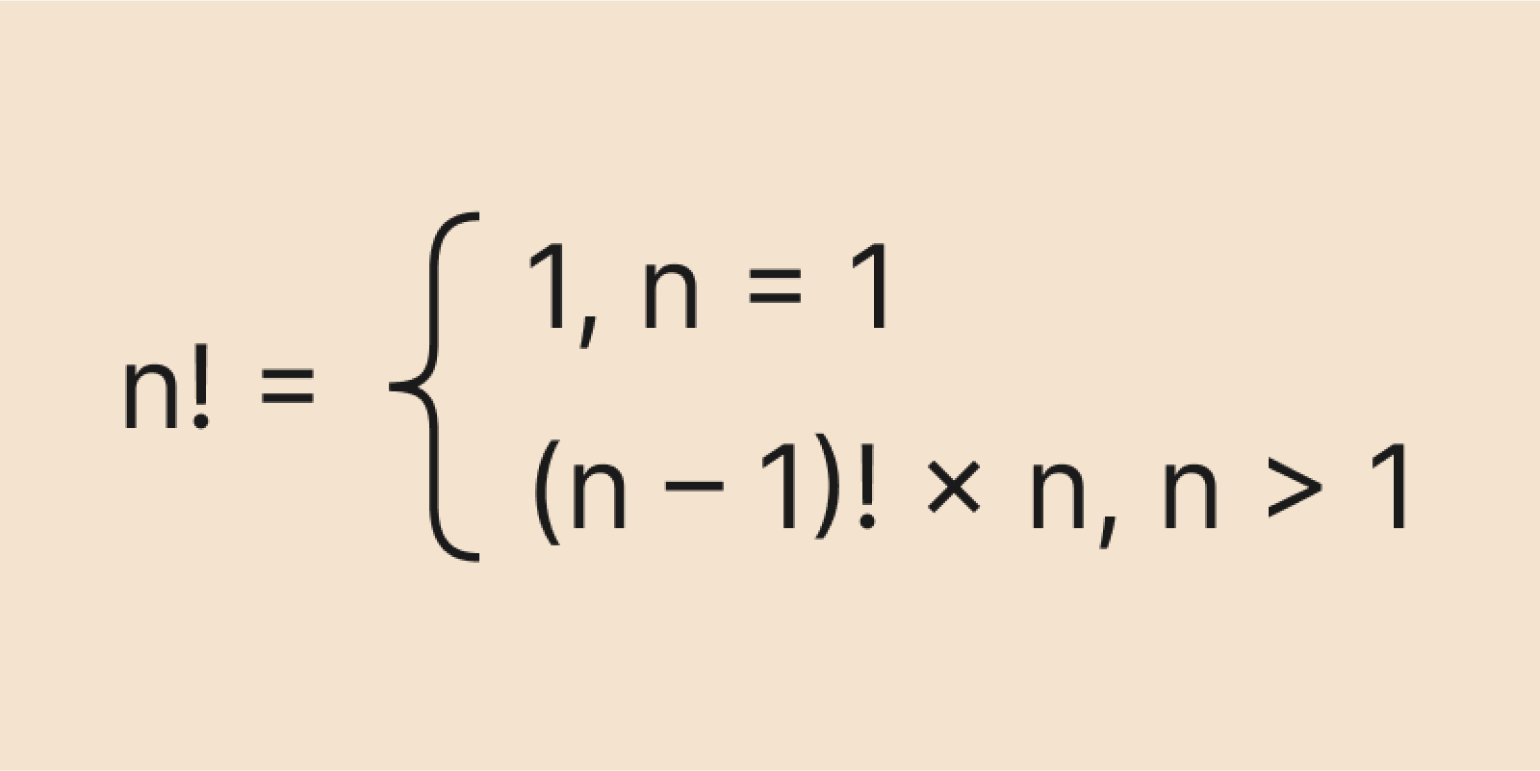
Изображение: Skillbox Media

Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.

Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:

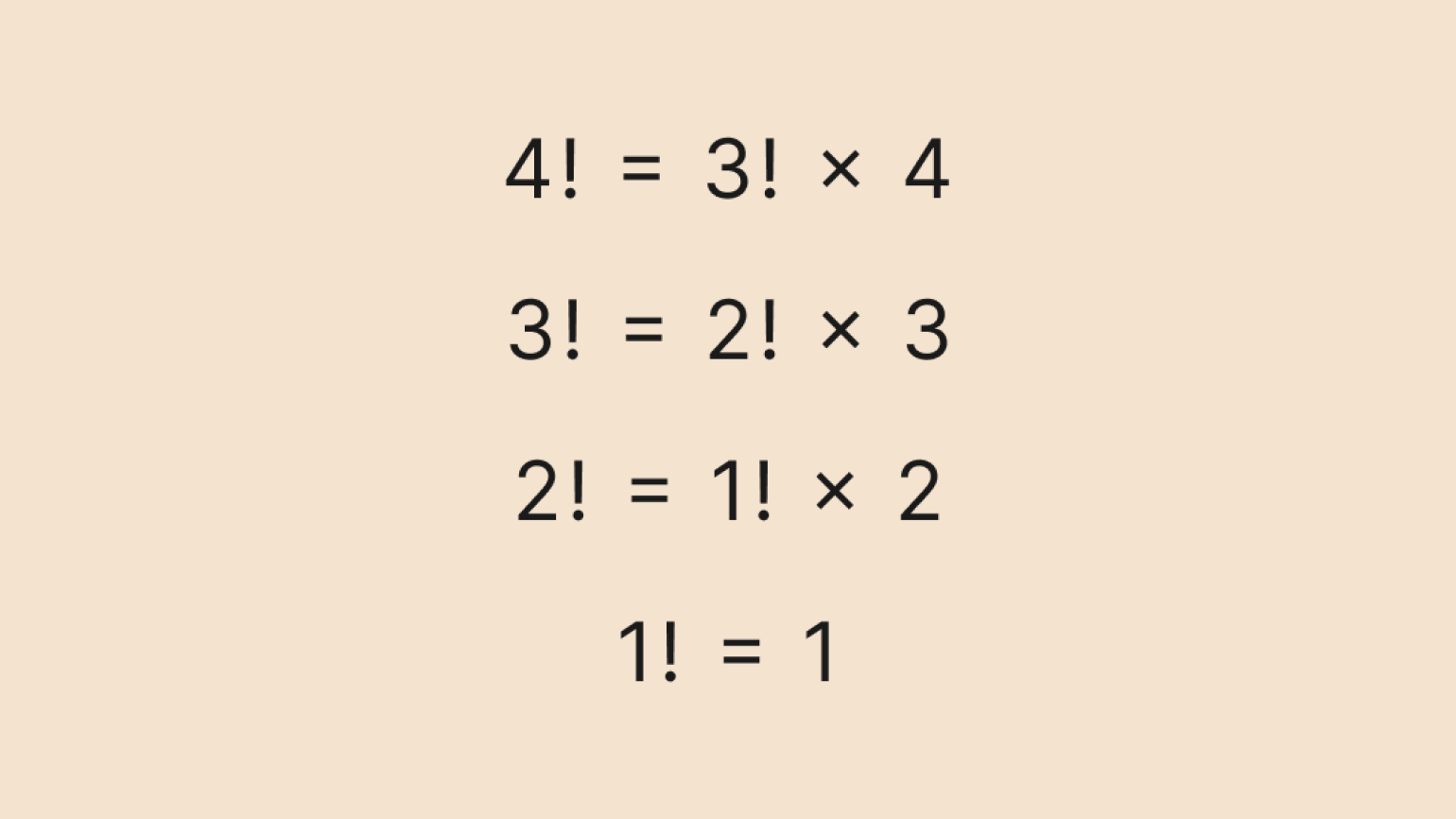
Изображение: Skillbox Media

Можно записать это и в сокращённом виде:

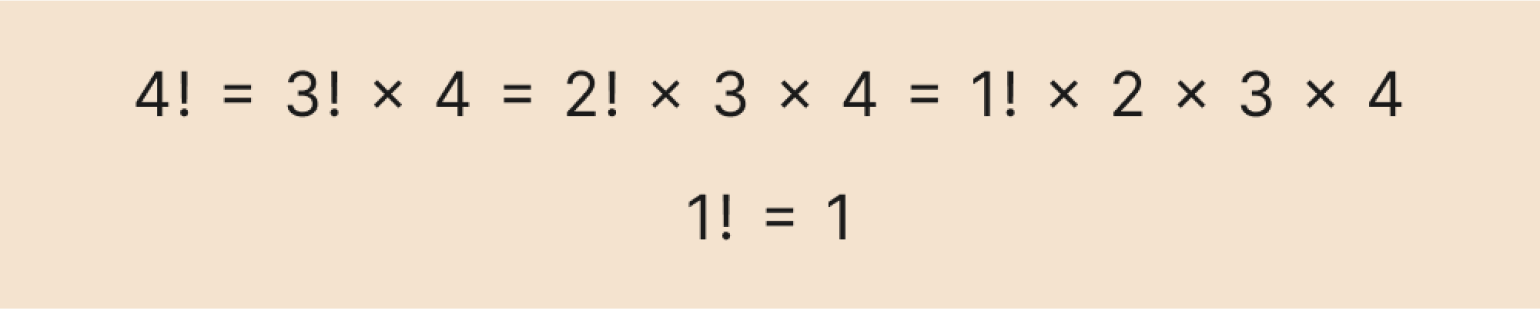
Изображение: Skillbox Media

Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:

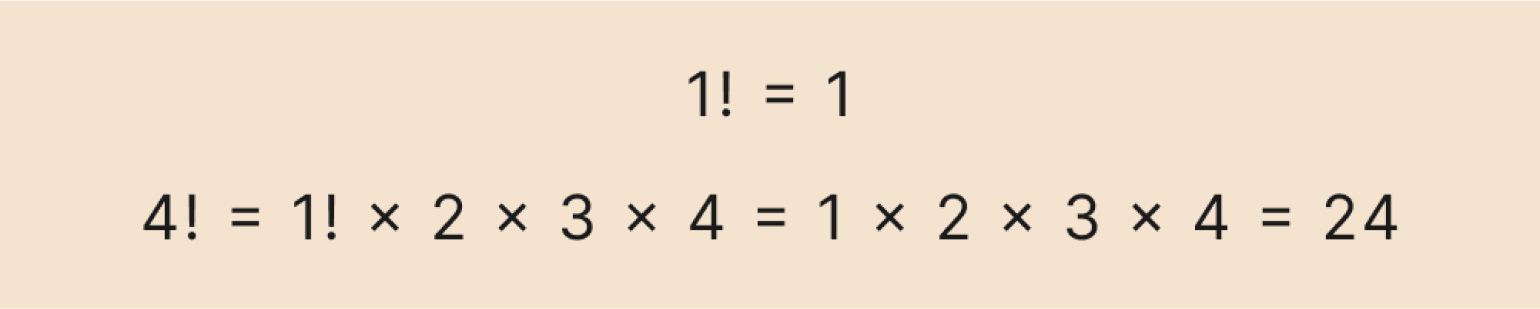
Изображение: Skillbox Media

Получили ответ — 24. Ничего сложного, просто перемножаем числа.

Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:

Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.

Правила использования восклицательного знака перед числом

Примеры:

1!	Я не мог поверить своим глазам!
100!	Это было невероятное достижение!
42!	Ответ на главный вопрос жизни, Вселенной и всего такого!

Использование восклицательного знака перед числом позволяет привлечь внимание читателя и подчеркнуть важность числовой информации. Однако, следует помнить, что он должен использоваться с умом и соблюдением грамматических правил

Выделение живой речи

В письменной речи восклицательный знак перед числом можно рассматривать как оператор, который подчеркивает эмоциональность высказывания. Например:

«Ого, уже 10 часов!» — выражение удивления о том, что время прошло быстро.

Таким образом, восклицательный знак перед числом помогает выделить живую речь и передать эмоциональность высказывания.

Обозначение громкости

Удивление, вызывающее внимание, может быть выражено с помощью восклицательного знака перед числом. В программировании это обозначает оператор, который указывает на необходимость обратить внимание на конкретное значение или действие

В контексте громкости, восклицательный знак перед числом обычно означает, что громкость является максимальной или наивысшей. Например, в таблице ниже представлены различные уровни громкости, обозначенные с помощью восклицательного знака.

Обозначение громкости
Уровень громкости
!
Максимальная громкость
!!
Очень высокая громкость
!!!
Очень высокая громкость, вызывающая внимание

Таким образом, использование восклицательного знака перед числом позволяет четко указать на необходимость обратить внимание на определенное значение или действие, в данном случае — уровень громкости

Выделение рекламных предложений

Восклицательный знак перед числом в рекламных предложениях часто используется для привлечения внимания потенциального клиента

Он означает, что предложение имеет особую выгоду или уникальность, которая может вызывать удивление и привлечь внимание

Оператор «!» перед числом добавляет в рекламное предложение эмоциональную окраску и призывает к более активному вниманию со стороны потребителя. Такие предложения часто используются в рекламе товаров и услуг, чтобы выделить их среди конкурентов и создать эффект чисто.

Например, рекламное предложение «Скидка 50%!» привлекает внимание покупателей своей акцией, предлагающей значительную скидку. Или предложение «Бесплатная доставка!» обращает внимание на бесплатность услуги доставки, что может быть привлекательным для потенциальных клиентов

Таким образом, использование восклицательного знака перед числом в рекламных предложениях помогает привлечь внимание и вызвать интерес со стороны потребителей, помогая выделиться среди конкурентов и стимулировать продажи