Название чисел

Содержание

В десятой части есть место для 100 тысячных, и чтобы убедиться, необходимо учесть, что единицу можно разделить на 10, 100, 1000 или более равных частей, что удобно, поскольку работать с дробями с этими знаменателями особенно легко.

Первым делом необходимо установить значение терминов десятые, сотые и тысячные:

• Если агрегат разделен на 10 равных частей, одна из них называется одна десятая.
• Разделив единицу на 100 равных частей, каждая одна сотая.
• Наконец, если его разделить на 1000 равных частей, одна из них будет одна тысяча.

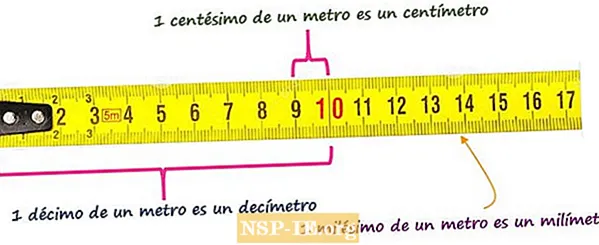
Вы можете продолжать до бесконечности, разделяя единицу на все меньшие и меньшие равные части, например, 10000, это одна десятитысячная, затем будут продолжаться стотысячные и так далее, но на данный момент этого достаточно, чтобы достичь тысячных.

В любом случае, чем на большее количество частей разделен агрегат, тем меньше будет каждая из них. Следовательно, десятая часть больше сотой, а эта, в свою очередь, больше тысячной и десятитысячной.

Имея это в виду, одна десятая содержит 10 сотых, а это, в свою очередь, 10 тысячных. Поскольку десятая часть имеет 10 сотых, а каждая сотая — 10 тысячных, из этого следует, что 1 десятая имеет 10 × 10 тысячных = 100 тысячных.

Десятичные дроби и десятичные числа

Использование десятых, сотых, тысячных и более широко распространено в повседневной жизни. Например, они используются при измерении длины рулеткой или при покупке продуктов питания и напитков, цены на которые обычно выражаются в песо, евро, долларах … за каждый килограмм, 100 граммов, литров или миллилитров продукта.

Для всех этих целей обычно используется метрическая система. Эта система измерений является общепринятой и основана на степени 10. Это означает, что каждая из составляющих ее единиц соотносится с другими в степени 10.

Разделив единицу на степень 10, как объяснялось в начале, получим следующее: десятичные дроби и соответствующее ему выражение в десятичные числа:

• Десятые: 1/10 = 0.1
• Сотые: 1/100 = 0.01
• Тысячные = 1 / 1000 = 0.001
• Десять тысячных = 1 / 10.000 = 0.0001
• Сто тысячных = 1/ 100.000 = 0.00001
• Миллионных = 1 / 1.000.000 = 0.000001

Естественно, вы можете разделить любое число, кроме 1, на степень 10 и получить десятичные дроби. Сделать это очень просто, вам просто нужно переместить десятичную запятую влево, столько разрядов, сколько нулей, имеют силу, например:

• Две десятых: 2/10 = 0,2
• Пять сотых: 5/100 = 0,05
• Восьми тысячные: 8/1000 = 0,008

Точно так же десятичное число может быть представлено десятичной дробью, как показано ниже:

• 57.9 = 579 / 10
• 101.03 = 10103/100

Десятичные числа читаются путем указания сначала количества единиц, затем десятых, затем сотых и так далее, например, предыдущие числа читаются следующим образом:

• 57,9 — это 57 единиц и 9 десятых
• 101,03 равно 101 единиц, 0 десятых и 3 сотых.

Десятичная дробь

Десятичная дробь — это дробь, знаменатель которой равен 10, 100, 1000, 10000 или любой другой степени 10, отсюда и слово десятичное. Например, 2/1000, 53/10, 2781/100, 321/1000 являются десятичными дробями.

Когда записывается десятичная дробь, знаменатель опускается и ставится знак (десятичная точка), чтобы указать значение числа.

В номере числителя и справа от запятой должно быть столько чисел, сколько нулей имеет соответствующий знаменатель.

примеров

— 2/10000 будет записано как 0,0002.

— 53/10 будет написано как 5.3.

— 2781/100 записывается как 27,81.

— 321/1000 записывается как 0,321.

С другой стороны, дробь, которая представляет номер предыдущего изображения, равна 3,152 / 100, поскольку число имеет две цифры справа от десятичной точки..

Число слева от запятой называется «целой частью», а число справа — десятичной частью..

Влияние на окружающую среду

Сотая миллиметра – это крайне малая единица измерения, однако она может иметь значительное влияние на окружающую среду. Вот несколько примеров того, как одна сотая миллиметра может повлиять на окружающую среду:

1. Поверхностный сток. Сотая миллиметра осадков может привести к образованию поверхностного стока, который является потоком воды, протекающим по поверхности земли. Этот сток может переносить загрязнения, такие как пестициды, нефтепродукты и другие токсичные вещества, которые накапливаются на поверхности земли. Постепенно эти загрязнения могут попадать в реки, озера и другие водные водоемы, нанося значительный вред экосистемам.

2. Затопление. Хотя одна сотая миллиметра осадков может показаться незначительным количеством, в некоторых случаях это количество может быть достаточно для вызывания затопления. Это может произойти, если земля уже насыщена водой и не может впитать дополнительные осадки. Затопление может нанести большой ущерб сельскому хозяйству, инфраструктуре, жилым зданиям и привести к потере жизней и эвакуации населения.

3. Воздействие на растительность. Даже такое незначительное количество осадков, как одна сотая миллиметра, может иметь влияние на растительность. Для некоторых растений это может быть недостаточным количеством влаги для роста и выживания. В засушливых регионах, такое незначительное количество осадков может усугубить ситуацию и привести к сельскому хозяйственному неурожаю.

4. Образование льда. Даже незначительное количество осадков в виде дождя или снега может привести к образованию льда на дорогах и тротуарах. Это может вызвать опасность для автомобилей и пешеходов, приводя к дорожным авариям и травмам.

5. Изменение водного баланса. Одна сотая миллиметра осадков может оказывать влияние на водный баланс региона. В регионах с низкими осадками такое незначительное количество может быть ощутимым для доступности питьевой воды и использования в промышленности и сельском хозяйстве.

В заключение, хотя одна сотая миллиметра может показаться малозначительной, она может иметь серьезное влияние на окружающую среду

Поэтому важно принимать во внимание все аспекты погоды и осадков для планирования и принятия мер, направленных на устойчивое использование ресурсов и сохранение окружающей среды

Как читать десятичные дроби

Поддержать сайт

В первую очередь обсудим вид десятичной дроби.
Каждая цифра после запятой имеет своё название. Десятые, сотые, тысячные, десятитысячные…

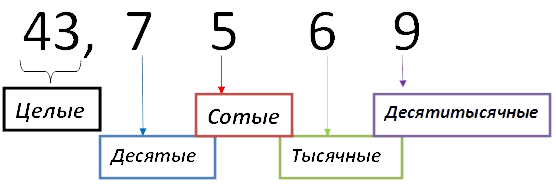
Десятые, сотые и тысячные

Попробуем прочитать десятичную дробь из примера выше.
Чтобы правильно прочитать десятичную дробь нужно:

• Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится
  целая часть десятичной дроби. Читаем: «сорок три целых».

• Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».

• Добавить в конце название самой правой цифры.У нас это9, которая стоит на месте десятитысячных
  (см. рис. выше):
  «десятитысячных».

Значит, полное название дроби звучит так:

43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.

Справа от запятой после самой последней
правой цифры отличной от нуля можно добавлять сколько угодно
нулей. От этого значение десятичной дроби не изменится.

Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим
такую же по значению десятичную дробь.

Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем
ноль на конце и записываем:

Запомните!

Нули можно добавлять (убирать) только после самой последней правой отличной от нуля
цифры. Нули между цифрами в числе убирать нельзя.

Формула тысячной

Формула, показывающая взаимосвязь дальности до цели, высоты (длины) цели и ее угловой величины называется формулой тысячной и применяется не только в артиллерии, но и в военной топографии: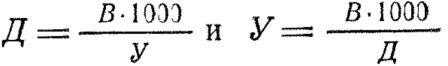

где:

Д — дальность до предмета в метрах

У — угол, под которым виден предмет в тысячных

В — высота (ширина) предмета в метрах

В получившемся результате может быть погрешность в 5 %, что можно игнорировать для большинства практических расчётов.

Есть правило для лучшего запоминания соотношения: «предмет, линейным размером 1 метр, удалённый от наблюдателя на 1 километр, виден под угловой величиной в 1 тысячную».

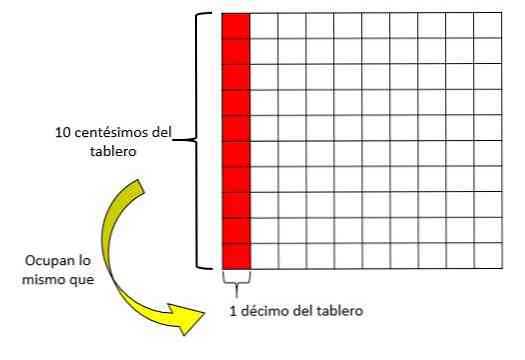
Сколько сотых может уместиться в десятой?

Из того, что написано выше, известно, что десятая равна 1/10, а сотая — 1/100. В десятичной записи у нас будет десятая 0,1, а сотая 0,01.

Ключ к ответу на этот вопрос состоит в том, чтобы знать, сколько раз вам нужно добавить сотую часть с собой, так что результат будет лишь десятой.

Если мы выполним вычисления, вы увидите, что вы должны добавить 1 сотую 10 раз с собой, чтобы получить десятую.

Поэтому в десятый вписывается 10 центов.

Другой процесс, который мы можем использовать, чтобы узнать, сколько сотых вписывается в десятую часть, заключается в следующем: берется доска с 100 квадратами, затем 1 квадрат доски представляет сотую, а любой столбец (или ряд) из 10 квадратов представляет 1 десятую часть доски.

Итак, чтобы заполнить ряд (1 десятая), вам нужно 10 квадратов (10 сотых).

ссылки

1. Бурдон, П. Л. (1860). Элементы Арифметики. Мадрид: Книжный магазин Дона Анхеля Каллеха.
2. Высший институт педагогической подготовки (Испания); Хесус Лопес Руис. (2004). Числа, формы и объемы в детской среде. Министерство образования.
3. Мандри Ф. (1837). Теоретические упражнения арифметики. Кампания и Дети.
4. Мартинес, J. C. (2014). Математическая компетентность N2. Ideaspropias Редакция С.Л..
5. Матеос, М. Л. (2013). Королевский прямой. Лопес Матеос Эдиторес.
6. Palmer, C.I. & Bibb, S.F. (1979). Математические практики: арифметика, алгебра, геометрия, тригонометрия и правила вычислений (Переиздание ред.). Реверте.

Как записывается и читается тысячная

Тысячные записываются и читаются соответственно так:

• одна тысячная — 0,01 — ноль, ноль один
• шесть тысячных — 0,06 — ноль, ноль шесть
• 25 тысячных — 0,25 — ноль, двадцать пять
• 130 тысячных- 1,30 — один, тридцать
• 1500 тысячных — 15,00 — пятнадцать, ноль ноль

Как производится измерение тысячных

Определение угла по приборам. Измерение углов в тысячных может производиться угломерным кругом артиллерийской буссоли, сеткой бинокля и перископа, шкалой боковых поправок и лимбами маховика снайперского прицела, а также подручными предметами.

Буссоль имеет шкалу на круге, разделенную на большие деления в 1-00 и малые в 0-20.
Бинокль и перископ имеют сетки, разделенные на большие деления в 0-10 (десять тысячных) и малые в 0,05 (пять тысячных).
Прицелы пулеметные и снайперские имеют деления в 0,01 (одну тысячную). Пример: Определение дистанции или размеров объекта с помощью прицела ПСО-1

Глазомерное определение угла заключается в сопоставлении измеряемого угла с известным. Углы определенной величины можно получить следующими способами. Прямой угол получается между направлением рук, одна из которых вытянута вдоль плеч, а другая — прямо перед собой. От составленного таким приемом угла можно отложить какую-то часть его, имея в виду, что 1/2 часть соответствует углу 7-50 (45°), 1/3 — углу 5-00 (30°) и т.д. Угол 2-50 (15°) получается путем визирования через большой и указательный пальцы, расставленные под углом 90° и удаленные на 60 см от глаза, а угол 1-00 (6°) соответствует углу визирования на три сомкнутых пальца: указательный, средний и безымянный.

Угловые величины между пальцами руки

Определение угла по циферблату часов. Часы держат перед собой горизонтально и поворачивают их так, чтобы штрих, соответствующий 12 часам на циферблате, совместился с направлением левой стороны угла. Не меняя положения часов, замечают пересечение направления правой стороны угла с циферблатом и отсчитывают количество минут. Это и будет величина угла в больших делениях угломера. Например, отсчет 25 минут соответствует 25-00.

Определение угла компасом. Визирное приспособление компаса предварительно совмещают с начальным штрихом лимба, а затем визируют по направлению левой стороны измеряемого угла и, не меняя положения компаса, против направления правой стороны угла снимают отсчет по лимбу. Это и будет величина измеряемого угла или его дополнение до 360° (60-00), если подписи на лимбе идут против хода часовой стрелки.
Величину угла компасом можно определить более точно, измерив азимуты направлений сторон угла. Разность азимутов правой и левой сторон угла будет соответствовать величине угла. Если разность получится отрицательной, то необходимо прибавить 360° (60-00). Средняя ошибка определения угла этим способом составляет 3-4°.

С помощью линейки. Если линейку держать на расстоянии 50 см от глаз, то деление в 1 мм будет соответствовать 0-02. При удалении линейки от глаз на 60 см 1 мм соответствует 6′, а 1 см — 1°. Для измерения угла в тысячных линейку держат перед собой на расстоянии 50 см от глаз и подсчитывают число миллиметров между предметами, обозначающими направления сторон угла. Полученное число умножают на 0-02 и получают величину угла в тысячных. Для измерения угла в градусах порядок действий тот же, только линейку необходимо держать на расстоянии 60 см от глаз.
Точность измерения углов с помощью линейки зависит от умения выносить линейку точно на 50 или на 60 см от глаз. В этой связи можно рекомендовать следующее: к артиллерийскому компасу привязывается шнурок такой длины, чтобы линейка компаса, повешенного на шею и отнесенного вперед на уровень глаза наблюдателя, оказывалась от него на расстоянии ровно 50 см.

Измерение угла линейкой, удаленной на 50 см от глаза наблюдателя

Формула тысячной

Формула, показывающая взаимосвязь дальности до цели, высоты (длины) цели и ее угловой величины называется формулой тысячной и применяется не только в артиллерии, но и в военной топографии: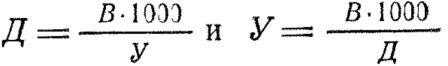

где:

Д — дальность до предмета в метрах

У — угол, под которым виден предмет в тысячных

В — высота (ширина) предмета в метрах

В получившемся результате может быть погрешность в 5 %, что можно игнорировать для большинства практических расчётов.

Есть правило для лучшего запоминания соотношения: «предмет, линейным размером 1 метр, удалённый от наблюдателя на 1 километр, виден под угловой величиной в 1 тысячную».

Сравнение десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.

Получить результат сравнения десятичной дроби с натуральным числом позволяет сравнение целой части данной дроби с данным натуральным числом. При этом периодические дроби с периодами 0
или 9
нужно предварительно заменить равными им конечными десятичными дробями.

Справедливо следующее правило сравнения десятичной дроби и натурального числа
: если целая часть десятичной дроби меньше данного натурального числа, то и вся дробь меньше этого натурального числа; если целая часть дроби больше или равна данному натуральному числу, то дробь больше данного натурального числа.

Рассмотрим примеры применения этого правила сравнения.

Пример.

Сравните натуральное число 7
с десятичной дробью 8,8329…
.

Решение.

Так как данное натуральное число меньше, чем целая часть данной десятичной дроби, то это число меньше данной десятичной дроби.

Ответ:

7

Пример.

Сравните натуральное число 7
и десятичную дробь 7,1
.

3.4 Правильный порядок
В предыдущем разделе мы сравнивали числа по их положению на числовой прямой. Это хороший способ сравнивать величины чисел в десятичной записи. Этот способ работает всегда, но это трудоемко и неудобно делать всякий раз, когда нужно сравнить два числа. Существует другой хороший способ выяснить, какое из двух чисел больше.

Пример A.

Рассмотрим числа из предыдущего раздела и сравним 0,05 и 0,2.

Чтобы выяснить, какое число больше, сравним сначала их целые части. Оба числа в нашем примере имеют равное количество целых — 0. Сравним тогда их десятые части. Число 0,05 имеет 0 десятых, а число 0,2 имеет 2 десятых. То, что число 0,05 имеет 5 сотых, ни имеет значения, поскольку десятые доли определяют, что число 0,2 больше. Мы можем, таким образом, записать:

Оба числа имеют 0 целых и 6 десятых, и мы пока не можем определить, какое из них больше. Однако, число 0,612 имеет всего 1 сотую часть, а число 0,62 – две. Тогда, мы можем определить, что
0,62 > 0,612

То, что число 0,612 имеет 2 тысячных, не играет роли, оно все равно меньше, чем 0,62.

Мы можем это проиллюстрировать на картинке:

	0,612
	0,62

Для того, чтобы определить, какое из двух чисел в десятичной записи больше, нужно сделать следующее:

1. Сравнить целые части. То число, у которого целая часть больше и будет больше.

2
. Если целые части равны, сравнить десятые части. То число, у которого десятых частей больше, и будет больше.

3
. Если десятые части равны, сравнить сотые части. То число, у которого сотых частей больше, и будет больше.

4
. Если сотые части равны, сравнить тысячные части. То число, у которого тысячных частей больше, и будет больше.

Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее — дробной:

5,28
5 — целая часть
28 — дробная часть

Дробная часть десятичной дроби состоит из десятичных знаков
(десятичных разрядов):

• десятые — 0,1 (одна десятая);
• сотые — 0,01 (одна сотая);
• тысячные — 0,001 (одна тысячная);
• десятитысячные — 0,0001 (одна десятитысячная);
• стотысячные — 0,00001 (одна стотысячная);
• миллионные — 0,000001 (одна миллионная);
• десятимиллионные — 0,0000001 (одна десятимиллионная);
• стомиллионные — 0,00000001 (одна стомиллионная);
• миллиардные — 0,000000001 (одна миллиардная) и т. д.

• прочитать число, составляющее целую часть дроби и добавить слово «целых
  «;
• прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.

Например:

• 0,25 — ноль целых двадцать пять сотых;
• 9,1 — девять целых одна десятая;
• 18,013 — восемнадцать целых тринадцать тысячных;
• 100,2834 — сто целых две тысячи восемьсот тридцать четыре десятитысячных.

Поиск ответа

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Ответ справочной службы русского языка

Сравнение десятичных дробей

Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел .

1. сначала сравниваются целые части дробей — больше будет та десятичная дробь у которой больше ее целая часть;
2. если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения — больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,28
   3 > 1,27
   9, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.

Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.

Например:

Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.

Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.

Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».

Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.

К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.

Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.

Чтение целой части десятичной дроби такое же, как и натуральных чисел.

Например:
27,5 — двадцать семь…;
1,57 — одна…

После целой части десятичной дроби произносится слово «целых».

Например:
10.7 — десять целых семь десятых

0,67 — ноль целых шестьдесят семь сотых.

Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.

• 1-й разряд после занятой — разряд десятых
• 2-й разряд после запятой — разряд сотых
• 3-й разряд после запятой — разряд тысячных
• 4-й разряд после запятой — разряд десятитысячных
• 5-й разряд после запятой — разряд стотысячных
• 6-й разряд после запятой — разряд миллионных
• 7-й разряд после запятой — разряд десятимиллионных
• 8-й разряд после запятой — разряд стомиллионных

В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.

Перевод десятичной дроби в смешанную дробь
состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.

Правила сравнения десятичных дробей, примеры, решения

После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.

Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей
: больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.

Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.

Пример.

Сравните десятичные дроби 9,43
и 7,983023…
.

Решение.

Очевидно, данные десятичные дроби не равны. Целая часть конечной десятичной дроби 9,43
равна 9
, а целая часть бесконечной непериодической дроби 7,983023…
равна 7
. Так как 9>7
(смотрите сравнение натуральных чисел), то 9,43>7,983023
.

Ответ:

9,43>7,983023
.

Пример.

Какая из десятичных дробей 49,43(14)
и 1 045,45029…
меньше?

Решение.

Целая часть периодической дроби 49,43(14)
меньше, чем целая часть бесконечной непериодической десятичной дроби 1 045,45029…
, следовательно, 49,43(14)

Ответ:

49,43(14)
.

Если целые части сравниваемых десятичных дробей равны, то для выяснения, какая из них больше, а какая — меньше, приходится сравнивать дробные части. Сравнение дробных частей десятичных дробей проводится поразрядно
— от разряда десятых к более младшим.

Для начала рассмотрим пример сравнения двух конечных десятичных дробей.

Пример.

Выполните сравнение конечных десятичных дробей 0,87
и 0,8521
.

Решение.

Целые части данных десятичных дробей равны (0=0
), поэтому переходим к сравнению дробных частей. Значения разряда десятых равны (8=8
), а значение разряда сотых дроби 0,87
больше, чем значение разряда сотых дроби 0,8521
(7>5
). Следовательно, 0,87>0,8521
.

Ответ:

0,87>0,8521
.

Иногда, чтобы выполнить сравнение конечных десятичных дробей с разным количеством десятичных знаков, к дроби с меньшим количеством десятичных знаков приходится дописывать некоторое количество нулей справа. Достаточно удобно уравнивать количество десятичных знаков до начала сравнения конечных десятичных дробей, дописав к одной из них некоторое количество нулей справа.

Пример.

Сравните конечные десятичные дроби 18,00405
и 18,0040532
.

Решение.

Очевидно, данные дроби неравны, так как их записи отличаются, но при этом они имеют равные целые части (18=18
).

Перед поразрядным сравнением дробных частей данных дробей уравняем количество десятичных знаков. Для этого припишем две цифры 0
в конце дроби 18,00405
, при этом получим равную ей десятичную дробь 18,0040500
.

Значения десятичных разрядов дробей 18,0040500
и 18,0040532
равны вплоть до стотысячных, а значение разряда миллионных дроби 18,0040500
меньше значения соответствующего разряда дроби 18,0040532
(0

Ответ:

18,00405

При сравнении конечной десятичной дроби с бесконечной, конечная дробь заменяется равной ей бесконечной периодической дробью с периодом 0
, после чего проводится сравнение по разрядам.

Пример.

Сравните конечную десятичную дробь 5,27
с бесконечной непериодической десятичной дробью 5,270013…
.

Решение.

Целые части данных десятичных дробей равны. Значения разрядов десятых и сотых данных дробей равны, и чтобы выполнить дальнейшее сравнение, конечную десятичную дробь заменяем равной ей бесконечной периодической дробью с периодом 0
вида 5,270000…
. До пятого знака после запятой значения разрядов десятичных дробей 5,270000…
и 5,270013…
равны, а на пятом знаке имеем 0

Ответ:

5,27

Сравнение бесконечных десятичных дробей также проводится поразрядно
, и заканчивается после того, как только значения какого-то разряда оказываются разными.

Пример.

Сравните бесконечные десятичные дроби 6,23(18)
и 6,25181815…
.

Решение.

Целые части данных дробей равны, также равны значения разряда десятых. А значение разряда сотых периодической дроби 6,23(18)
меньше разряда сотых бесконечной непериодической десятичной дроби 6,25181815…
, следовательно, 6,23(18)

Ответ:

6,23(18)

Пример.

Какая из бесконечных периодических десятичных дробей 3,(73)
и 3,(737)
больше?

Решение.

Понятно, что 3,(73)=3,73737373…
и 3,(737)=3,737737737…
. На четвертом знаке после запятой поразрядное сравнение заканчивается, так как там имеем 3

Ответ:

3,(737)
.