Основные сведения об окружности в геометрии

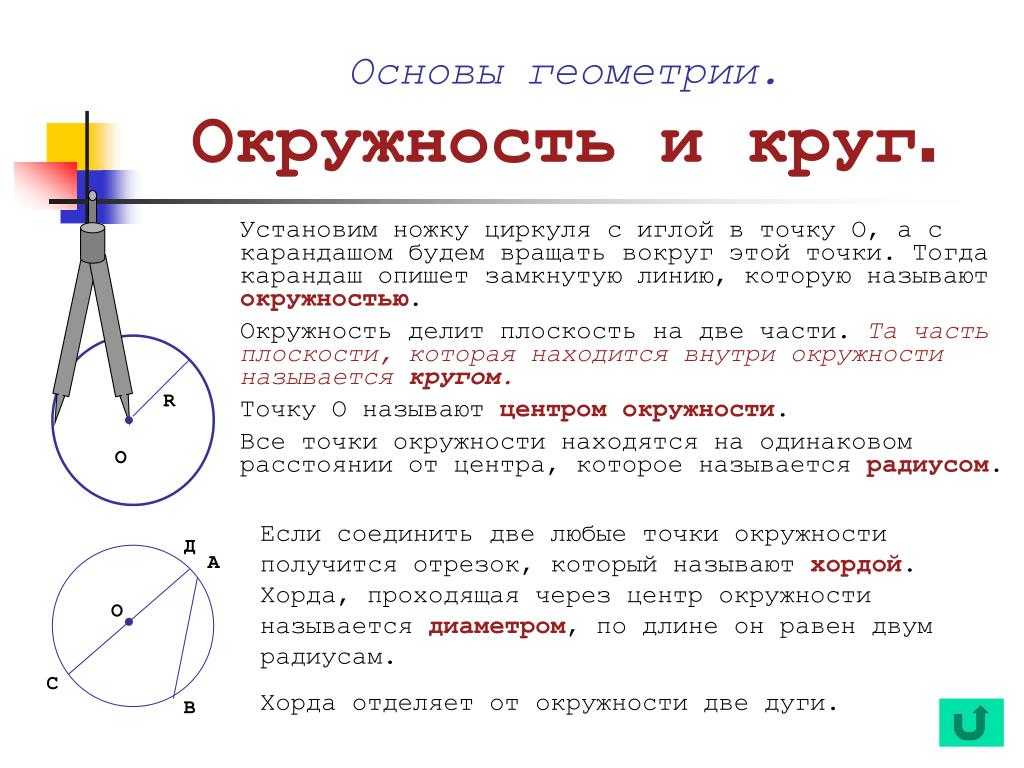
Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

1. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
2. С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
3. Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
4. Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
5. Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
6. Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

1. Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
2. Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
3. Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
4. Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
5. Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
6. Отрезок с наименьшей длиной представляет собой точку.
7. Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.

Круг

Окружность — это фигура, которая представляет собой замкнутую кривую линию, состоящую из всех точек, равноудаленных от данной точки, называемой центром окружности.

Форма круга является симметричной и имеет бесконечное количество осей симметрии.

Радиус круга представляет собой расстояние от мидпоинта окружности до ее центра.

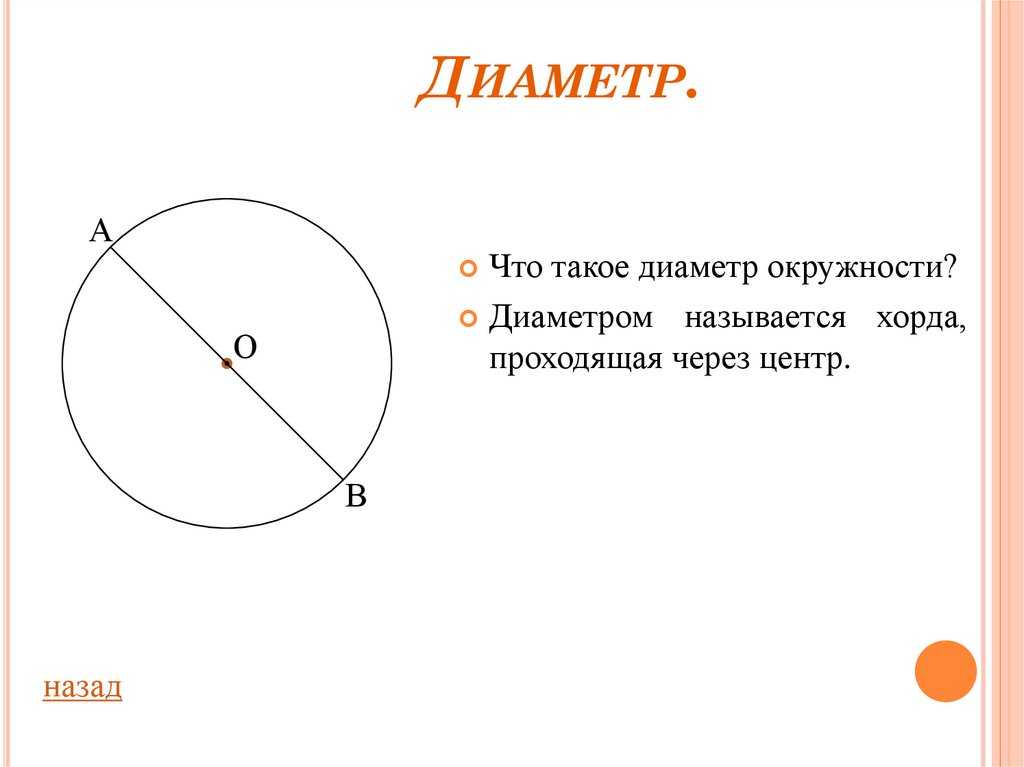
Диаметр круга — это отрезок, который соединяет две противоположные точки на окружности, проходящий через ее центр.

Площадь круга — это количество площади, занимаемое кругом на плоскости. Она вычисляется по формуле: S = πr², где π — постоянное число, равное приблизительно 3.14159, r — радиус круга.

Круг является одной из основных фигур в геометрии и имеет множество применений в различных областях науки и практической деятельности.

Определение и свойства

У окружности есть несколько важных характеристик. Радиус — это расстояние от центра окружности до любой её точки. Окружность также имеет диаметр — это отрезок, соединяющий две противоположные точки на окружности, проходящие через её центр. Диаметр равен удвоенному значению радиуса.

Площадь круга — это количество плоскости, которое содержится внутри его границы. Она вычисляется по формуле:

S = π * r^2.

где S — площадь круга, π (пи) — математическая константа, примерное значение которой равно 3,14, r — радиус круга.

Формула круга

Для определения площади круга используется формула:

1. Найдите диаметр круга, который представляет собой отрезок, соединяющий две точки на окружности и проходящий через центр.
2. Разделите диаметр пополам, чтобы найти радиус, который является расстоянием от центра до любой точки на окружности.
3. Возведите радиус в квадрат.
4. Умножьте полученное значение на число Пи (π), которое приближенно равно 3,14159.
5. Полученное произведение и будет площадью круга.

Формула площади круга:

S = π * r2

Где:

• S — площадь круга;
• π (Пи) — математическая константа, приближенно равная 3,14159;
• r — радиус окружности.

Используя формулу площади круга, можно вычислить его территорию, то есть площадь, занимаемую кругом.

Примеры использования

Окружность — это геометрическая фигура, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от заданной точки. Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. По своей форме окружность представляет собой замкнутую кривую с одной границей.

Круг — это геометрическая фигура, образованная всеми точками плоскости, которые находятся на определенном расстоянии от заданной точки, и сама эта точка — центр круга. Также круг определяется его радиусом, который является расстоянием от центра до любой точки на окружности. Круг представляет собой фигуру, ограниченную окружностью. Территория, заключенная внутри круга, называется площадью круга.

Примеры использования окружности и круга можно найти во многих областях жизни. Например, в архитектуре использование окружностей и кругов позволяет создавать красивые и эстетически приятные формы зданий и сооружений. В инженерии они применяются для создания колес и шестерен, а также для моделирования движений и процессов. В географии и картографии окружности используются для построения меридианов и параллелей на географических картах.

Понимание различий и применение окружностей и кругов помогает визуализировать и анализировать различные формы и границы, а также решать различные задачи в области геометрии и других наук.

Альфа — символ в магии

У магов считается, что выражение «Я есть Альфа и Омега» можно сказать одним словом «Альфа», так как Альфа — символ Омеги в движении.

Приобретая свое направление, верхняя часть Омеги вытягивается и заостряется. Однако стабильный символ О не дает Омеге сжаться в нижней части. Разделяющая черта, вызванная внутренним напряжением, дает толчок к появлению Альфы. Только усилие воли человека способно его создать.

До тех пор, пока маг устремлен к чему-либо, и его действия подчинены этой цели, он может распоряжаться Альфой, и возможности его становятся безграничными.

«Я есть Альфа и Омега, первый и последний…» — это клятва магов, которую они дают сами себе и получают возможность применения магии, которая может быть использована как в конструктивных, так и в деструктивных целях.

У магов считается, что в случаях, когда Альфа-символ ставится рядом с Омегой, то они, противореча друг другу, не могут быть полезными и способны даже нанести вред.

Взаимное отношение хорд и их расстояний от центров

Изобразим окружность и ее элементы, согласно теореме:

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

.

Попробуем доказать следующее:

.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные OA и OB равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины AB. В таком случае, точка C равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

.

Получаем, что перпендикуляр OC делит на две равные части дугу AB, что и требовалось доказать.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Перенесем данные на рисунок:

Запишем равенство двух хорд AB и CD:

AB = CD

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF

Если соединить между собой точки A и C, а также центральную точку O, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = = OF.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CDравноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

Таким образом, теорема доказана:

AB = CD

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC

Требуется доказать следующее:

OD < OE

Заметим, что OD расположен перпендикулярно относительно AB. Линия OF является наклонной. В таком случае:

OD < OF

Запишем, что:

OF < OE

В результате теорема доказана:

OD < OE

Интересные свойства омеги

Омега — понятие, зависящее от контекста, однако в геометрии она имеет несколько интересных свойств:

• Омега в треугольниках: Омега может быть использована для обозначения угла в треугольнике. Один из способов обозначить угол — это использование буквы «О» или заштрихованным омегой. Например, ОABC обозначает угол BAC. Это позволяет нам легко идентифицировать углы и работать с ними в геометрических вычислениях.
• Омега в геометрической алгебре: В геометрической алгебре омега часто используется для обозначения ориентации ортонормального базиса. Он может описывать положение пространственного вектора относительно базиса и позволяет легко выполнять операции, такие как поворот и симметрию.
• Омега в многогранниках: Омега может быть использована для обозначения грани многогранника. Если многогранник имеет n граней, то каждая грань может быть обозначена как О1, О2, …, Оn. Это помогает нам упорядочить и идентифицировать грани многогранника.

Таким образом, омега в геометрии имеет различные свойства и может быть использована для обозначения углов, ориентаций и граней в различных контекстах.

Омега в современной математике

Омега — один из символов, которые широко используются в современной математике. Этот символ имеет множество различных значений и применений в различных областях математики.

Омега используется в теории графов и комбинаторике для обозначения максимальной степени вершины в графе или графовых структурах. Например, если вершина имеет максимальную степень 3, то она обозначается как «вершина омега». Это понятие играет важную роль при анализе и классификации графов.

Омега также используется в теоретической физике и математической физике для обозначения угловой скорости вращения тела или потока

В этом контексте омега является важной физической величиной, которая определяет движение и динамику системы

В области комплексного анализа омега обозначает комплексное число, которое является положительным квадратным корнем из -1. Вместе со своим комплексно сопряженным числом -омега, оно образует комлексную плоскость, которая играет важную роль в решении уравнений и анализе функций, отображений и дифференциала.

Еще одним примером использования омега в современной математике является его применение в комбинаторных алгоритмах и решении задач оптимизации. Омега может обозначать изменение переменных, шаги алгоритма или просто служить символом для обозначения неопределенного значения.

Кроме того, омега широко используется в различных контекстах математического анализа, численных методов, теории вероятностей и многих других областях математики. В каждом из этих контекстов омега имеет свое значение и применение, которые обусловлены особенностями и требованиями соответствующей области.

Таким образом, омега в современной математике является многофункциональным символом, который используется в различных областях и контекстах математики. Его применение и значения зависят от конкретных задач и целей, которые ставит математик или физик.

Формула омеги в геометрии 8 класс

Формула омеги в геометрии 8 класс используется для вычисления площади треугольника, если известны длины его сторон. Формула представлена следующим образом:

ω = √(p·(p-a)·(p-b)·(p-c))

Где ω — площадь треугольника, p — полупериметр треугольника (p = (a + b + c)/2), a, b, c — длины сторон треугольника.

Формула омеги основана на формуле Герона, которая также используется для вычисления площади треугольника.

Для использования формулы омеги в геометрии 8 класс необходимо знать длины сторон треугольника. Поэтому перед использованием формулы необходимо провести измерение сторон треугольника с помощью линейки или другого инструмента измерения.

Формула омеги является одним из инструментов геометрии, который помогает решать задачи на нахождение площадей треугольников и других многоугольников. Знание и умение применять формулу омеги позволяет ученикам 8 класса успешно справляться с задачами на геометрию и решать геометрические задачи на ЕГЭ и других экзаменах.

Как выглядит тату и где ее лучше набивать

Татуировка символ альфа и символ омега может выглядеть по-разному. Но, как бы там ни было, эти две буквы не разрывают, так как по отдельности они не несут никакого смысла.

Обычно саму татуировку выполняют черной краской без дополнительных цветов и оттенков. Буквы переплетают между собой крест-накрест. В некоторых случаях мастера используют тени.

Рисуют татуировку чаще на голени, либо на руках (по одной букве на каждой)

. На правой стороне обычно изображают альфу, а на левой – омегу. Иногдапредставители сильного пола набивают такую татуировку на спине в области лопаток , как бы изображая крест из букв, аженщины – на одном из запястья , чаще на левой руке (крест-накрест).

Хорда и радиус

Между этими понятиями существуют следующие связи:

1. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
2. Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
3. Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
4. Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
5. Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
6. Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Геометрия: понятие и особенности

Геометрия — раздел математики, изучающий пространственные формы, их свойства и взаиморасположение.

В основе геометрии лежит понятие точки. Точка — это абстрактный объект, не имеющий размеров, но обладающий положением в пространстве.

Два или более точки могут образовывать прямую, которая является бесконечно узкой и простирается в одном направлении.

Если две прямые имеют общую точку, они пересекаются и образуют угол. Угол — это область пространства между двумя лучами, имеющая начальную точку и конечную точку.

Одна из основных особенностей геометрии — изучение фигур. Фигура — это ограниченная область пространства, образованная линиями и/или поверхностями. Примерами фигур являются треугольник, квадрат, круг.

Для описания и изучения фигур в геометрии используются различные свойства. Например, длина сторон, площадь, объем, углы и т. д.

Геометрия также изучает преобразования фигур. Преобразования — это изменения положения и формы фигуры без изменения ее размеров. Примерами преобразований являются поворот, отражение, сдвиг.

Одной из важных тем в геометрии является трехмерная геометрия. Трехмерная геометрия изучает пространственные фигуры, которые имеют три измерения: длина, ширина и высота. Примерами трехмерных фигур являются куб, сфера, цилиндр.

В общем, геометрия — это наука, позволяющая нам понять и описать физическое пространство, его формы и свойства. Она является основой для различных инженерных и архитектурных решений, а также широко применяется в научных исследованиях и различных областях жизни.

Комплексная геометрия: омега и другие концепции

Комплексная геометрия является разделом математики, который исследует геометрические объекты и операции с использованием комплексных чисел. Она позволяет решать сложные задачи, которые не всегда могут быть решены с помощью классической геометрии.

Один из ключевых концепций комплексной геометрии является понятие «омега». Омега — это комплексное число, которое соответствует точке плоскости или объекту в трехмерном пространстве. Омега может представлять собой координаты точки или вектора.

Свойства омеги позволяют выполнять различные операции, такие как сложение, вычитание, умножение и деление, которые позволяют производить с ними арифметические действия. Благодаря этим операциям можно строить сложные фигуры и находить решения задач.

Омега также используется для описания поворотов и смещений объектов. При помощи комплексных чисел можно выполнять повороты вокруг точек или осей, а также осуществлять смещения на заданные величины. Это позволяет изучать динамическую геометрию и анимацию объектов.

Помимо омеги, в комплексной геометрии существуют и другие концепции, такие как аргумент и модуль комплексного числа. Аргумент — это угол между вектором и положительным направлением оси. Модуль — это длина вектора, которая отображает его абсолютное значение. Эти понятия часто используются для описания свойств и связей объектов в геометрии.

Комплексная геометрия находит применение в различных областях, таких как физика, компьютерная графика, робототехника и криптография. Она является мощным инструментом для моделирования и анализа сложных систем и может быть полезной в решении разнообразных задач.

Конец цикла

Символ омега часто используется в еврейском искусстве и архитектуре. чтобы символизировать конец цикла или завершение задачи. В синагоге ковчег, в котором хранятся свитки Торы, часто украшается символом омега, указывающим на то, что свитки представляют собой конец одного цикла чтения и начало нового.

Символ омега также используется в изучении еврейского мистицизма. В каббале Древо Жизни изображается с 10 соединенными между собой сферами, или сефиротами. Последняя сефира, называемая Малхут, связана с символом омега и представляет физический мир. Говорят, что это последний шаг в процессе творения и начало нового цикла.

Как ухаживать за татуировкой

Как только мастер набил тату, он обязан наложить на тот участок кожи повязку из бинта или обернуть пищевой пленкой. Открывать тату рекомендуется не позже, чем через 24 часа, в зависимости от сложности и размера рисунка, а также от вида перевязочного материала. Если это пищевая пленка, стоит сделать перевязку уже через 3-4 часа, дав коже «подышать». Бинт разрешается держать до суток.

Во время перевязки нужно обязательно тату промывать. Делать это можно или обычной водой с мылом без отдушки, либо специальными средствами (по советам мастера). Нельзя использовать мочалки и включать сильно горячую или холодную воду. От этого тату будет заживать еще дольше. Рекомендуется сделать воду комнатной температуры.

Интересное: Значение тату перо для девушек и парней

Татуировку нужно промокать насухо, желательно обычными бумажными полотенцами. Далее стоит нанести на кожу специальное средство для заживления, о котором также можно узнать у мастера. Мыть тату необходимо каждый день на протяжении 3-4 недель с использованием лосьонов и кремов, ведь правильный уход влияет и на качество готовых изображений.

Вы всегда можете обратиться в любой тату-салон, и они Вам нарисуют понравившееся вам тату быстро и качественно. Если же от вас будет предоставлена фотография с татуировкой, подобрать и нарисовать нужный рисунок получится гораздо быстрее.

Подводя итоги, хотелось бы сказать, что татуировка альфа и омега, выполненная крест-накрест – это отличный выбор для мудрого, религиозного, но при этом воинствующего человека, который готов принимать серьезные решения, взяв на себя ответственность. Удачи в выборе!

Омега: основные принципы геометрии 8 класса

В геометрии 8 класса углы могут быть различными: острыми, прямыми, тупыми, полными и отрицательными. Острый угол имеет меньшую меру 90 градусов. Прямой угол равен 90 градусам. Тупой угол имеет меру больше 90 градусов и меньше 180 градусов. Полный угол равен 180 градусам. Отрицательный угол имеет меру меньше нуля.

Для измерения углов используется градусная мера. Градус — это единица измерения углов. Полный угол равен 360 градусам. При измерении прямого угла используется 90 градусов. Очень часто в геометрии 8 класса омега используется для обозначения острых и тупых углов. Для прямого угла обычно используется специальный символ – квадрат. В таблице ниже представлены примеры обозначения углов:

Тип угла	Обозначение
Острый угол	ω
Прямой угол	□
Тупой угол	ω

Омега – это важный символ в геометрии 8 класса, который помогает обозначить углы и различные их типы. Знание основных принципов омеги позволяет ученикам более точно воспринимать и работать с геометрическими формами и объектами.

омега

Омега — это название последней буквы греческого алфавита (двадцать четвертого). Термин омега имеет значение «конец», когда используется, связанный с первой буквой греческого алфавита «альфа», например, в выражении «альфа и омега», что означает «начало и конец».

В физике графическое представление заглавной буквы Ω и строчной буквы ω используется в разных контекстах. В качестве единицы измерения электрического сопротивления (Ом) используется заглавная буква Ω. Строчная буква ω может быть переменной, которая представляет угловую скорость тела или угловую частоту LC-контуров (измеряется в радианах в секунду).

Расчет объема с использованием омеги

Перед тем, как погрузиться в расчеты, давайте вспомним, что такое объем. Объем — это мера пространства, занимаемого телом. Например, если у нас есть параллелепипедный аквариум, мы можем рассчитать его объем, чтобы узнать, сколько воды нужно для его заполнения.

Для начала, у нас должны быть известны основные параметры тела, для которого мы хотим рассчитать объем. Например, если мы хотим найти объем шара, нам потребуются данные о его радиусе.

Итак, как же использовать омегу для расчета объема? Омега может быть использована для нахождения объема различных геометрических фигур. Например, для шарового сегмента, объем можно вычислить по следующей формуле:

V = (2 * П * R^2 * H) / 3,

где V — объем, П — число Пи (не путать с пирогом!), R — радиус, H — высота.

Для других геометрических фигур тоже можно использовать омегу для расчета объема. Например, для цилиндра, объем можно найти по следующей формуле:

V = П * R^2 * H,

где V — объем, П — число Пи, R — радиус основания цилиндра, H — высота цилиндра.

И так далее. Вы видите, омега помогает нам связать различные параметры фигур и выразить их объем в виде простой формулы. Это очень удобно и экономит время при решении геометрических задач.

Теперь давайте рассмотрим некоторые примеры. Представьте, что у вас есть шар с радиусом 5 сантиметров. Как найти его объем? Просто подставьте значения в формулу:

V = (2 * П * 5^2 * H) / 3.

Здесь, чтобы найти объем шара, вам нужно знать только его радиус. Просто подставьте значение радиуса в формулу и получите ответ. Это так легко!

Также не забывайте, что омега может быть использована для решения более сложных задач. Например, если вам нужно найти объем пересечения двух цилиндров, можно использовать омегу для каждого цилиндра и затем вычислить объем пересечения.

В итоге, использование омеги в расчете объема позволяет нам быстро и точно определить пространство, занимаемое геометрическими фигурами. Надеюсь, что сейчас вам стало понятнее, как использовать омегу и решать задачи по геометрии. Удачи вам в ваших математических приключениях!

Символическое представление омеги

Таким образом, символическое представление омеги в геометрии можно понять как обозначение оси или плоскости в пространстве. Омега — это символ, который помогает нам легче понять и визуализировать различные геометрические концепции.

Например, ось омега может быть использована для представления вектора или даже для определения плоских фигур. Этот символ также может быть полезен при решении геометрических задач и построении различных геометрических моделей.

Кроме того, символическое представление омеги может быть использовано для обозначения множества различных геометрических параметров, таких как углы, длины сторон, площади и объемы фигур. Омега позволяет нам легче работать с этими параметрами и применять их в практических расчетах.

Использование символического представления омеги в геометрии помогает нам облегчить понимание и визуализацию сложных геометрических концепций. Он является мощным инструментом для решения геометрических задач и построения геометрических моделей. Поэтому не стоит недооценивать этот символ и его значение в геометрии.

Итак, символическое представление омеги — это важный элемент геометрии, который помогает нам понять и визуализировать различные геометрические концепции. Он используется для обозначения осей, плоскостей, векторов, параметров фигур и многого другого. Использование омеги облегчает решение геометрических задач и позволяет нам применять геометрию в практической деятельности.