Что такое аксиома и теорема

Примеры применения

Пример 1:

Теорема о бесконечности простых чисел может быть применена при решении задачи о поиске простых чисел. Она утверждает, что существует бесконечное количество простых чисел, и это дает возможность найти новые простые числа при необходимости.

Пример 2:

Теорема Ферма-Эйлера, которая является основой теории остатков, может быть применена для решения задач, связанных с криптографией и безопасностью. Используя эту теорему, можно проверить, является ли число взаимно простым с другим числом, что полезно при шифровании и дешифровании данных.

Пример 3:

Теорема Питагора, которая формулирует соотношение между сторонами прямоугольного треугольника, может быть применена во множестве задач геометрии и физики. Она помогает находить значения неизвестных сторон треугольника или проверять, является ли данный треугольник прямоугольным.

Как понять, что теорема доказана

Доказательство теоремы — основной этап математической работы. От правильности доказательства зависит вся дальнейшая работа в данной области математики. Чтобы убедиться, что теорема доказана, необходимо выполнение нескольких критериев.

Логичность. Доказательство должно состоять из строго логических рассуждений. Каждое утверждение должно быть доказано на основе того, что было доказано ранее.
Переходы

Важно, чтобы каждый переход из одной формулы или теоремы в другую был верным. Необходимо следить за каждым шагом и убедиться, что он безусловно верный

Нет противоречий. В доказательстве не должно быть противоречий, то есть двух утверждений, которые не могут быть одновременно верными. При обнаружении противоречий необходимо их исправить или показать, почему они не противоречат друг другу.

После выполнения этих критериев можно считать, что теорема доказана

Но также важно заметить, что доказательство может быть открыто новым методом, что в дальнейшем потребует его уточнения и дополнения

Типы теорем и их характеристики

В математике существует несколько типов теорем, каждый из которых имеет свои характеристики и особенности. Они могут быть классифицированы по различным критериям, включая объем доказательства, уровень абстракции, геометрический или алгебраический характер, приложения в других областях математики или физики, и т. д.

Другой тип теорем — теоремы существования. Они утверждают, что объект существует, но необязательно единственный. Эти теоремы обычно имеют более сложные доказательства, и их приложения могут быть менее очевидными, чем у теорем о существовании и уникальности.

Ещё один тип теорем — теоремы равносильности. Они устанавливают, что два высказывания эквивалентны друг другу, то есть имеют одинаковую истинность в любых условиях. Эти теоремы могут быть полезны в логических рассуждениях и доказательствах сложных математических утверждений.

• Существуют также теоремы о пределе и непрерывности.
• Теоремы о дифференцируемости и интегрируемости функций.
• Теоремы о числовых рядах.

Теоремы могут быть связаны с различными математическими объектами, такими как функции, множества, графы и топологические пространства. Некоторые теоремы могут быть широко применяемыми, в то время как другие могут быть более специализированными и имеют значение только в определенных областях математики.

Теоремы обладают особенной ценностью в математике, поскольку они позволяют утверждать с уверенностью, что некоторое утверждение является истинным в любых условиях, что приводит к развитию других областей науки и технологии.

Неформальное изложение теорем

Логически многие теоремы имеют форму ориентировочного условное : если A, то B. Такая теорема не утверждает B — только то, что B является необходимым следствием A. В этом случае A называется гипотезой теоремы («гипотеза «здесь означает нечто очень отличное от гипотезы ), а B — заключение теоремы. В качестве альтернативы, A и B также могут быть названы антецедентом и следствием соответственно. Теорема «Если n — четное натуральное число, тогда n / 2 — натуральное число» является типичным примером, в котором гипотеза «n — четное натуральное число», а вывод — «n / 2 также является натуральным числом «.

Чтобы теорема была доказана, она должна быть в принципе выражена в виде точного формального утверждения. Однако теоремы обычно выражаются на естественном языке, а не в полностью символической форме — с предположением, что формальное утверждение может быть получено из неформального.

В математике принято выбирать несколько гипотез в рамках данного языка и заявлять, что теория состоит из всех утверждений, которые можно доказать на основе этих гипотез. Эти гипотезы составляют фундаментальную основу теории и называются аксиомами или постулатами. Область математики, известная как теория доказательств, изучает формальные языки, аксиомы и структуру доказательств.

планарнаяТеорема о четырех цветах

Некоторые теоремы «тривиальны »в том смысле, что они очевидным образом вытекают из определений, аксиом и других теорем и не содержат каких-либо удивительных идей. Некоторые, с другой стороны, могут быть названы «глубокими», потому что их доказательства могут быть длинными и трудными, затрагивать области математики, внешне отличные от формулировки самой теоремы, или показывать удивительные связи между разрозненными областями математики. Теорема может быть простой и глубокой. Прекрасным примером является Великая теорема Ферма, и есть много других примеров простых, но глубоких теорем в теории чисел и комбинаторике, среди других областей.

Другие теоремы имеют известное доказательство, которое нелегко записать. Наиболее яркими примерами являются теорема о четырех цветах и ​​гипотеза Кеплера. Обе эти теоремы становятся истинными только в результате сведения их к вычислительному поиску, который затем проверяется компьютерной программой. Первоначально многие математики не принимали эту форму доказательства, но она стала более широко распространенной. Математик Дорон Зейлбергер зашел так далеко, что заявил, что это, возможно, единственные нетривиальные результаты, которые когда-либо доказали математики. Многие математические теоремы могут быть сведены к более простым вычислениям, включая полиномиальные тождества, тригонометрические тождества и гипергеометрические тождества.

Теорема Фалеса

Приписывается греческому математику Фалесу из Милета (ок. 624 – c. 546 a. До н.э.), эта теорема из двух частей (или, скорее, эти две теоремы с одинаковым названием) касается геометрии треугольников следующим образом:

Первая теорема Фалеса гласит, что если одну из сторон треугольника продолжить дальше параллельной прямой, то получится больший треугольник тех же пропорций. Это можно выразить следующим образом:

Если даны два пропорциональных треугольника, один большой, другой маленький, то коэффициент двух сторон большого треугольника (A и B) всегда будет равен коэффициенту тех же сторон маленького треугольника (C и D)

A/B = C/D

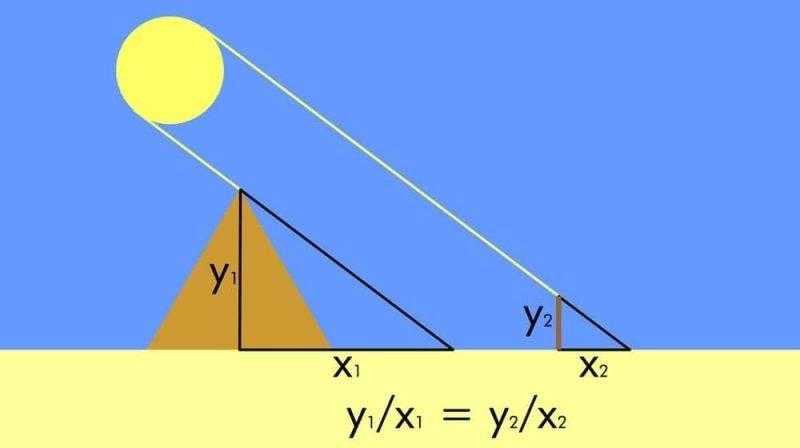
Эта теорема послужила, согласно греческому историку Геродоту, Фалесу для измерения размеров пирамиды Хеопса в Египте, без необходимости использовать инструменты огромных размеров

Вторая теорема Фалеса гласит, что из окружности, диаметр которой равен AC, с центром O (отличным от A и C), можно построить правильный треугольник ABC такой, что

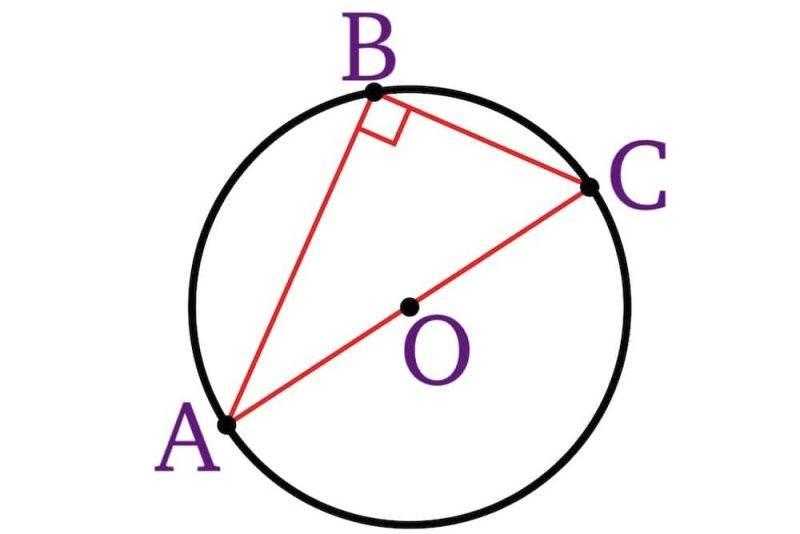
Отсюда вытекают два следствия:

1. В любом правильном треугольнике длина медианы, соответствующей гипотенузе, всегда равна половине гипотенузы.
2. Окружность любого правильного треугольника всегда имеет радиус, равный половине гипотенузы, а ее центр будет расположен в середине гипотенузы.

Схема

Теорема и ее доказательство обычно излагаются следующим образом:

Теорема (имя человека, который ее доказал, а также год открытия или публикации доказательство).

Формулировка теоремы (иногда называемая предложением).

Доказательство .

Описание доказательства.

Конец

Об окончании доказательства может свидетельствовать буквами QED (quod erat manifestrandum) или одним из знаков надгробия, таких как «□» или «∎», означающих «Конец доказательства», введенный Полом Halmos после их использования в журналах для обозначения конца статьи.

Точный стиль зависит от автора или публикации. Многие публикации предоставляют инструкции или макросы для набора в домашнем стиле.

Обычно теореме предшествуют определения, описывающие точное значение терминов, используемых в теорема. Также обычно теореме предшествует ряд предложений или лемм, которые затем используются в доказательстве. Однако леммы иногда вкладываются в доказательство теоремы либо с вложенными доказательствами, либо с их доказательствами, представленными после доказательства теоремы.

Следствия теоремы приводятся либо между теоремой и доказательством, либо сразу после доказательства. Иногда следствия имеют собственные доказательства, объясняющие, почему они следуют из теоремы.

Слайды и текст этой презентации

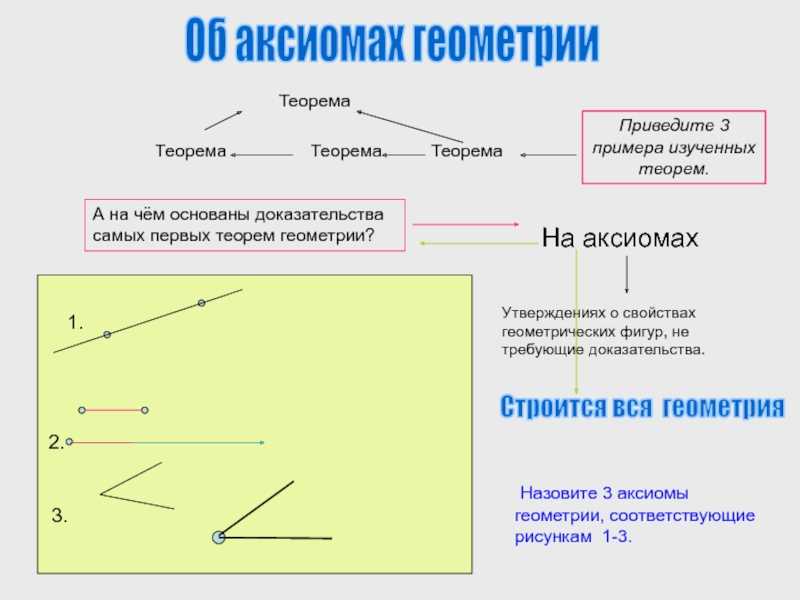
Слайд 5Теорема Теорема

Теорема ТеоремаОб аксиомах геометрииА

на чём основаны доказательства самых первых теорем геометрии?

На аксиомах

Утверждениях о свойствах геометрических фигур, не требующие доказательства.

2.

Приведите 3 примера изученных теорем.

Назовите 3 аксиомы геометрии, соответствующие рисункам 1-3.

1.

3.

Строится вся геометрия

Слайд 6Сначала формулируются исходные положения — аксиомыНа их основе, путём логических

рассуждений доказываются другие утверждения Такой подход к построению геометрии зародился

в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида

365 – 300 гг. до н.э.

Геометрия, изложенная в «Началах», называется евклидовой геометрией

Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии

Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

Слайд 8Нам представляется, что через т. М нельзя провести прямую (отличную

от прямой в), параллельную прямой а.А можем ли мы это

доказать?

Ответ на этот непростой вопрос дал великий русский математик Н.И. Лобачевский. Он выяснил, что это утверждение доказать нельзя, т.к. само является аксиомой.

Слайд 9Аксиома параллельных прямыхАЧерез точку, не лежащую на прямой проходит только

из аксиом и теорем.

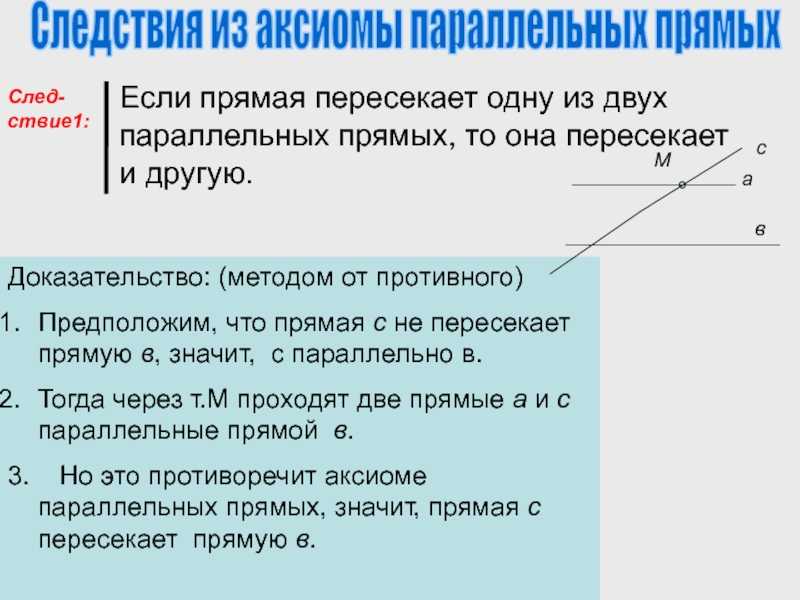
Слайд 10 Если прямая пересекает одну из двух параллельных

прямых, то она пересекает и другую.

Следствия из аксиомы параллельных прямых

Доказательство: (методом от противного)Предположим, что прямая с не пересекает прямую в, значит, с параллельно в.Тогда через т.М проходят две прямые а и с параллельные прямой в.3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.

След-ствие1:

от противного)Предположим, что прямая а и прямая в пересекаются.2.

Тогда через т.М проходят две прямые а и в параллельные прямой с3 . Но это противоречит аксиоме параллельных прямых.4. Значит прямые а и в параллельны.

След-ствие 2:

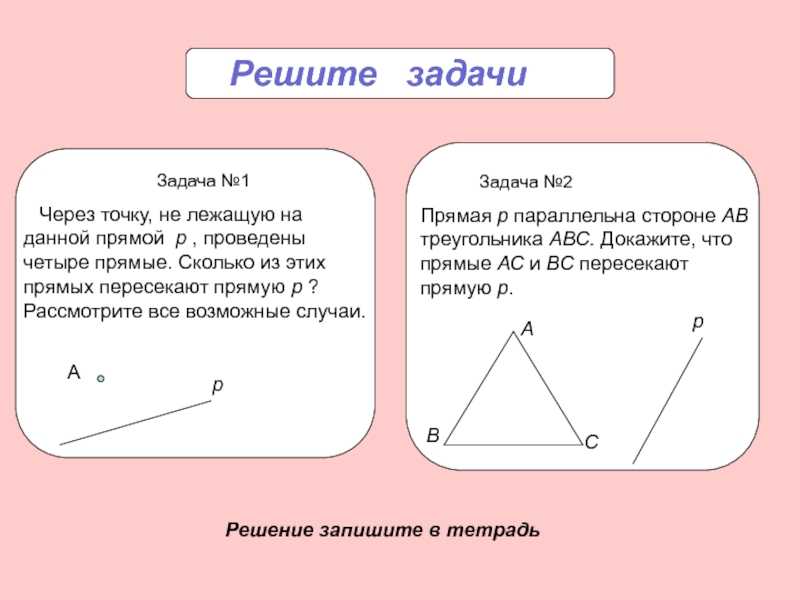
Слайд 12 Решите задачи

Задача №1 Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.

А

р

Задача №2Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АС и ВС пересекают прямую р.

А

В

С

р

Решение запишите в тетрадь

Слайд 14Любую теорему можно записать так, чтобы различить условие и заключение.

Например: Если углы вертикальные, то они равны.2) Если треугольник

равнобедренный, то углы при его основании равны.

Условие:

Заключение:

углы равны

Слайд 17Выполните тест, ответы запишите в тетрадь.Тест по теме «Аксиомы»

1. Основные объекты геометрии – это… 2. Аксиома –

это утверждение, а) получаемое путем логического доказательства, б) истинность которых принимается без доказательства, в) которое требуется доказать 3. Теорема – это утверждение, … 4.Кто автор работы «Начала»? 5. Из каких частей состоит теорема? 6. Назовите условие и заключение в 1 признаке параллельности прямых.

Спасибо за внимание! Успехов в работе по изучению геометрии!

Аксиоматический метод и его структура

Забавно, но аксиоматический метод упрощенно можно представить в виде фамильного древа. Рассмотрим его схематику: за точку «отсчета» берется набор аксиом, на основе которых далее формируются предположения. Если истинность предположения подтверждается путем доказательства, оно становится теоремой.

Примечание. Знание каких-либо аксиом или теорем на данном этапе совершенно необязательно. Ваша основная задача — просто понять, как связаны все эти элементы схемы выше. Далее мы этим и займемся.

Доказательство в геометрии — важный «связующий мостик» между предпосылками и подтвержденными утверждениями. Вообще, аксиоматический метод задает бесконечный маршрут: путь «от одного к другому» можно проделывать нескончаемо долго, используя ранее доказанные теоремы в качестве фундамента для формирования новых предположений и теорем.

Что такое аксиома?

А теперь о вкусном, и у нас, друзья, неприятность: из холодильника пропал торт. Предположим, ваша задача — доказать, что не совсем-то он и пропал. Его просто кто-то съел. Ваш внутренний Шерлок включается в игру, и вы пытаетесь найти «следы преступления» на кухне.

РАСКРЫВАЕМ ДЕЛОВо-первых, глаз замечает шоколадные крошки на столешнице. Из этого вы заключаете, что его однозначно разрезали. Подкрепляет выводы и факт, что в раковине лежит разделочная доска со следами шоколада. Во-вторых, в мусорном ведре обнаруживается упаковочный материал с надписью «Торт шоколадный». Отлично, дело раскрыто!

Если бы не одно но… За поиски пропавшей сладости вы взялись, совершенно не думая, существует ли торт. Вы приняли как данность положение, что ранее в холодильнике находился торт. Никто не пытался доказывать его существование.

Или отсутствие. Задача стояла объемнее — доказать, что его съели. Так что существование торта — вот что такое аксиома. Шуточно, конечно.

Формально определение следующее:

Аксиома в составе «цепи»

Допустим, из утверждения $A$ вы доказываете утверждение $B$. Далее из $B$ вы заключаете истинность $C$. После, из $C$ выводите утверждение $D$, и так далее.

Если расположить данное следствие утверждений друг за другом, то получается, что аксиоматический метод — это цепь. Одно цепляется за другое. Однако до бесконечности идти в обратную сторону цепочки уже не получится — у цепной ветви должно быть начало, которое уже ни к чему не прикрепляется.  

{"questions":[{"content":"В цепочке выше — $A\\Rightarrow{B}\\Rightarrow{C}\\Rightarrow{D}$ — какое из утверждений будет считаться аксиомой? `choice-1`","widgets":{"choice-1":{"type":"choice","options":,"explanations":,"answer":}}}]}

Что такое теорема?

Теперь, когда мы условились, что такое аксиома (иными словами, приняли за истину ряд положений бездоказательно), у нас сформировался каркас, на основе которого можно строить дальше. Рассмотрим еще один, чуть более разветвленный граф, где будет наглядно показано, что такое теорема и как она связывается с аксиомой.

Структурно геометрию можно представить в виде подобного графа. Он, правда, будет гораздо сложнее в устройстве, если на нем расположить все теоремы.

К примеру, рассмотрим узел $H$. Для того, чтобы туда попасть, справа необходимо пройти через узел $F$ и одну из точек старта — $С$. Слева необходим узел $D$ и точка старта $A$. Чем больше узлов, тем сложнее путь.

{"questions":[{"content":"Думаем, и так понятно, однако на всякий случай вас проверим. На графе выше, какой элемент отвечает за теорему, а какой за аксиому? `matcher-1`","widgets":{"matcher-1":{"type":"matcher","labels":,"items":}}}]}

Ребра графа, они же стрелки, — это доказательства. Начиная со «стартовых» бездоказательных утверждений (аксиом), мы выводим первые прямые следствия (теоремы) — их доказательство опирается исключительно на истинность аксиом. Далее из полученных теорем мы предполагаем существование следующих из них теорем. Доказательство нового «пакета» теорем опирается на истинность первых следствий, которые, в свою очередь, опираются на истинность принятых изначально аксиом.

Мы наконец готовы дать определение тому, что такое теорема:

Так что такое теорема? Это клубочек. Клубочек даже самой комплексно составленной теоремы можно размотать до аксиом: от последней теоремы — к другим; от них — назад к еще одной теореме, от этой теоремы — еще к ряду других, далее-далее… Ура, аксиома. Путь, который вы проделываете, заматывая клубочек, — это и есть доказательство в геометрии.

Понятие аксиомы и о ее значении для теоремы

Аксиома – это основное утверждение, на котором строится теория математики. Она принимается без доказательства, как нечто самоочевидное и врожденное.

Значение аксиомы в теореме заключается в том, что они служат начальными положениями, от которых можно отталкиваться при доказательстве какой-либо теоремы.

Аксиомы важны для теоретической математики так как эта наука строит свои выводы и выводит свои теоремы на основе уже готовых аксиом, поэтому аксиомы играют ключевую роль в математических доказательствах.

Аксиомы бывают разного рода. Некоторые аксиомы называют «аксиомы пустоты», они предполагают наличие некоторых объектов на данном множестве. Другими словами, они устанавливают, что непустое множество должно иметь хотя бы один элемент. Или, например, аксиомы называют «аксиомы равенства», они устанавливают, что два объекта равны между собой, если и только если они идентичны по всем атрибутам.

Доказательство в геометрии: определение

И что такое аксиома рассмотрели, и что такое теорема разобрали. А сейчас — наиважнейший момент, ибо доказательство в геометрии будет на все следующие пять лет вашим, можно сказать, основным занятием. В принципе, если аналогия выше с клубочком была понятна, проследить за логикой математических доказательств труда не составит.  

Здесь уместно будет сразу дать определение, а потом его уже разобрать:

На основе аксиом выстраиваются предположения — они же предпосылки или гипотезы. Истинность предположений утверждается доказательством: в таком случае истинные предположения называются теоремами.  

Вспомним аналогию с тортом, только вкупе с математической структурой. В качестве аксиом мы бы взяли: существует торт, торт съедобен, торт хранится в холодильнике, торт упаковывается, и, главное, торт разрезается. Раз в холодильнике торт мы не обнаружили, это открывает возможность выдвинуть гипотезу: торт кто-то съел. Дабы проверить истинность гипотезы, нужно построить цепочку умозаключений — привести доказательство.

Посылка	Доказательство посылки (аксиома)
А. Торта нет в холодильнике.	Торт съедобен; торт хранится в холодильнике.
B. Крошки на столешнице.	Торт разрезается.
C. Разделочная доска со следами шоколада.	Торт разрезается.
D. Упаковочный материал в мусорном ведре.	Торт упаковывается.

Все посылки истинны, так как опираются на принятые в рамках «тортовой» системы аксиомы. Истинность посылок обеспечивает истинность вывода об истинности гипотезы. Приведение истинных посылок и вывода из них — процесс доказательства.

Что было выдвинуто. Гипотеза $C$ «торт кто-то съел».Вывод. $A$ и $B$ и $C$ и $D$ $\Rightarrow$ $C$.      

Аксиоматический метод дружит с дедуктивной логикой

Логика, которую мы применяли в течение доказательства гипотезы, называется дедуктивной. На основе общих положений — аксиом — мы вывели частное положение о том, что торт был съеден. Доказательство в геометрии имеет примерно такой же принцип: вам нужно придумать, как и в каком порядке воспользоваться имеющимися аксиомами и теоремами для того, чтобы что-то доказать.

Готовы решить реальную задачу?

Задача. Дан квадрат $ABCD$ и ромб $A_{1}B_{1}C_{1}D_{1}$. Известно, что сторона квадрата $AB$ равна стороне ромба $C_{1}D_{1}$. Докажите, что периметры квадрата и ромба равны.

Решение. Что мы все о тортах. Пора воспользоваться аксиоматическим методом напрямую! Панику отставить, ибо мы приведем все необходимые данные и облегчим решение. Ваше главное задание — проследить за реальной цепочкой умозаключений, то есть за доказательством в геометрии.

Начнем с анализа фигур. Строго говоря, далее будет вовсе не аксиома, а следствие из аксиом о точках и отрезках, но тем не менее выдвинем бездоказательно, что квадрат — фигура с прямыми углами, у которой все стороны равны. Еще одна для нас «аксиома»: ромб — тоже фигура с равными сторонами, но углами, отличными от прямых.

Далее воспользуемся заданным в условии положением о том, что сторона квадрата $AB$ равна стороне ромба $C_{1}D_{1}$. Раз все стороны в квадрате равны и все стороны в ромбе равны, делаем вывод:

$$AB=A_{1}B_1=BC=B_{1}C_{1}=CD=C_{1}D_{1}=AD=A_{1}D_{1}$$

Все стороны фигур меж собой равны. Если периметр — сумма всех сторон, тогда периметр заданного квадрата равен периметру заданного ромба. Что и требовалось доказать.

Обращаем ваше внимание, что дедуктивная логика доказательства опирается на связку «если… то», где «если»-посылка — общее утверждение, а «то»-вывод — частное заключение. Из общих «аксиом», применимых ко всем ромбам и квадратам, и заданных условием положений мы, путем доказательства, вывели положение, применимое только к квадрату и ромбу с равными сторонами

Из общих «аксиом», применимых ко всем ромбам и квадратам, и заданных условием положений мы, путем доказательства, вывели положение, применимое только к квадрату и ромбу с равными сторонами.  

$\textcolor{purple}{Если}$:

• у квадрата все стороны равны;
• у ромба все стороны равны;
• сторона квадрата по условию равна стороне ромба;
• периметр — сумма всех сторон;

$\textcolor{coral}{То}$:

• все стороны квадрата $ABCD$ равны всем сторонам ромба $A_{1}B_{1}C_{1}D_{1}$;
• значит, периметры фигур равны.

{"questions":[{"content":"Наша шуточная задача предполагает, что мы можем составить из последнего вывода теорему!  `choice-1``speech-4`","widgets":{"choice-1":{"type":"choice","options":,"answer":},"speech-4":{"type":"speech","text":"Выберите наиболее подходящий вариант текста теоремы для задачи."}}}]}

Что такое теорема?

Теорема – это предложение , которое на основе определенных предположений или гипотез может доказать тезис, который не является самоочевидным (поскольку тогда он был бы аксиомой ). Они очень часто встречаются в формальных языках , таких как математика или логика , поскольку представляют собой формулировку определенных формальных правил или правил игры

Теоремы не только предлагают устойчивые отношения между предпосылками заключением , но и предоставляют фундаментальные ключи для их доказательства. Доказательство теорем, по сути, является ключевой частью математической логики, поскольку из одной теоремы можно вывести другие теоремы и тем самым расширить знания о формальной системе

Однако в области математических исследований термин ‘теорема’ используется только для обозначения предложений, представляющих особый интерес для академического сообщества. В логике первого порядка, с другой стороны, любое доказуемое утверждение само по себе является теоремой

Слово теорема происходит от греческого theórema, образованного от глагола theorein, означающего созерцать, судить или размышлять, от которого также происходит слово теория

Для древних греков теорема была результатом тщательного и внимательного наблюдения и размышления, и этот термин очень часто использовался многими философами и математиками того времени. Отсюда происходит и научное различие между терминами ‘теорема’ и ‘проблема’: первый – теоретический, второй – практический

Каждая теорема состоит из трех частей:

• Гипотеза или предпосылки. Это логическое содержание, из которого может быть выведено заключение и которое, следовательно, предшествует ему.
• Тезисы или заключение. Это то, что указано в теореме и что может быть формально доказано из того, что предложено в предпосылках.
• Королларии. Это те вторичные и дополнительные умозаключения или формулировки, которые получаются из теоремы.

Вам может быть полезно: Логическое мышление

Теорема Пифагора

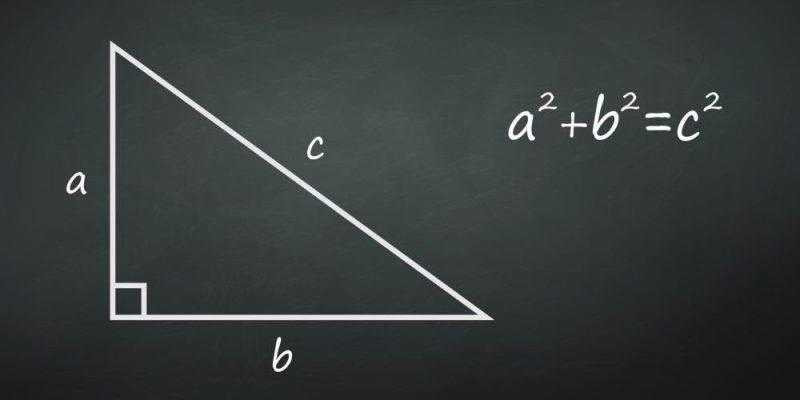Пифагорейская теорема – одна из самых древних математических теорем.

Теорема Пифагора – одна из древнейших математических теорем, известных человечеству. Она приписывается греческому философу Пифагору Самосскому (ок. 569 – c. 475 a.до н.э.), хотя считается, что теорема гораздо древнее, возможно, вавилонского происхождения, и что Пифагор был первым, кто ее доказал

Эта теорема утверждает, что если задан правильный треугольник (т.е. имеющий хотя бы один прямой угол), то квадрат длины стороны треугольника, противоположной прямому углу (гипотенуза), всегда будет равен сумме квадратов длин двух других сторон (называемых ногами). Это утверждается следующим образом:

В каждом правильном треугольнике квадрат гипотенузы равен сумме квадратов ножек

И со следующей формулой:

a2 + b2 = c2

Где a и b равны длине ног, а c – длине гипотенузы. Из этого также можно вывести три следствия, то есть производные формулы, которые имеют практическое применение и алгебраическую проверку:

a = √c2 – b2 . b = √c2 – a2 c = √a2 + b2

Пифагорейская теорема была доказана множество раз на протяжении истории: самим Пифагором и другими геометрами и математиками, такими как Евклид, Папп, Бхаскара, Леонардо да Винчи, Гарфилд и др

Теорема своими словами для детей

Теорема — это как загадка, которую мы должны разгадать, используя знания, которые мы уже имеем. Давай представим, что у нас есть пазл, и чтобы собрать его, нам нужно использовать разные кусочки, которые уже есть. Каждый из этих кусочков — это аксиома или ранее доказанная теорема.

Когда мы решаем теорему, мы соединяем эти кусочки вместе, чтобы получить полную картину или ответ на нашу загадку. Мы должны быть очень внимательными и логичными, чтобы правильно соединить кусочки и доказать теорему.

Зачем нам это нужно? Ну, когда мы доказываем теорему, мы показываем, что она всегда верна, не только для одного конкретного случая

Это очень важно для науки и математики, потому что это позволяет нам понять, как работают разные вещи и находить законы и правила, которые всегда действуют

Так что, когда мы решаем теорему, мы на самом деле играем в умные игры, чтобы узнать больше о мире вокруг нас. И кто знает, может быть, мы даже откроем что-то новое!

Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Теорема на academic.ru

Другие известные теоремы

Другими известными теоремами являются:

• теорема Птолемея. В любом циклическом четырехугольнике сумма произведений пар противоположных сторон равна произведению их диагоналей.
• Теорема Эйлера-Фермата. Если a и n – целые числа относительно простых, то n делит aᵩ(n)-1.
• теорема Лагранжа. Если f – непрерывная функция на замкнутом интервале a, b и дифференцируемая на открытом интервале (a, b), то существует точка c в (a, b) такая, что касательная к ней параллельна секущей через точки (a, f(a)) и (b, f(b)).
• Теорема Томаса. Она гласит, что если люди считают ситуацию реальной, то эта ситуация становится реальной в своих последствиях.

История открытия

История открытия теоремы обычно начинается с указания на первого ученого, который это открыл или сформулировал

Однако, зачастую многие идеи и совершения предшественников привели к финальной формулировке теоремы, поэтому важно учитывать их труд и вклад в развитие науки

Именно в процессе исследований и математического анализа ученые приходили к определенным закономерностям и заключениям, которые в итоге и сформировали основы теоремы. Однако, весь путь от первых наблюдений и предположений до окончательной формулировки был долгим и сложным.

Постепенно, с развитием математической науки и появлением новых методов и инструментов, ученым удалось добиться большего понимания и углубиться в изучение теоремы. Благодаря усилиям множества ученых, в итоге была получена окончательная формулировка теоремы и ее математическое доказательство.

Сегодня теорема является одной из основных и важных концепций в математике. Она нашла применение в различных областях науки и техники, и ее формулировка и доказательство служат основой для дальнейших исследований и открытий.

Какие существуют методы доказательства теорем

Доказательство теорем – это ключевой этап математических исследований. Существует несколько основных методов, при помощи которых можно доказать теорему. Рассмотрим некоторые из них.

• Доказательство от противного: В этом методе мы начинаем с предположения того, что теорема не верна, и затем показываем, что такое предположение приводит к противоречию. Из этого следует, что исходное предположение было ложным и теорема доказана.
• Индукция: Этот метод используется для доказательств теорем, которые верны для всех чисел из какой-то последовательности. Метод заключается в том, что теорема доказывается для некоторого начального числа, а затем показывается, что если теорема верна для некоего числа из последовательности, то она верна и для следующего числа.
• Доказательство методом примеров: Этот метод заключается в том, что мы приводим примеры, в которых теорема верна, и показываем, что это не случайно, а является нормой. Однако, этот метод не является полным доказательством и теорема может оставаться не доказанной, пока не будет найдено строгое доказательство.

Кроме основных методов, существуют и другие, менее распространенные

Однако, независимо от выбранного метода доказательства, важно следовать строгой и логической цепочке мышления, чтобы доказательство было корректным и внятным