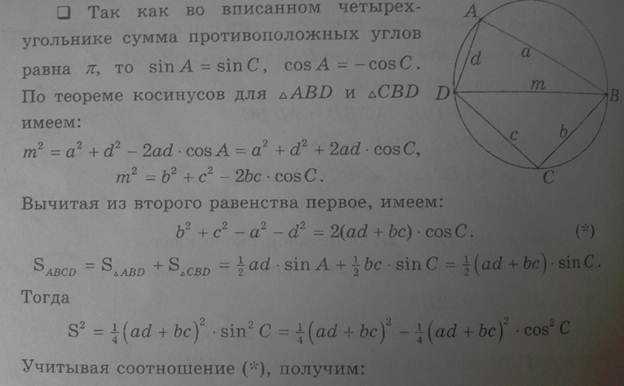Параллелограмм: свойства и признаки

Где встречаются геометрические фигуры в нашей жизни?

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. 

Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

И в современном мире без этих знаний не прожить.

Где же встречаются геометрические фигуры в нашей жизни?

Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр. 

Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия

Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте. 

Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.

Итак,

Диагональ прямоугольника

Определение.

Диагональю прямоугольника

Формулы определения длины диагонали прямоугольника

1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):

d
= √a
2 + b
2

2. Формула диагонали прямоугольника через площадь и любую сторону:

4. Формула диагонали прямоугольника через радиус описанной окружности:

d
= 2R

5. Формула диагонали прямоугольника через диаметр описанной окружности:

d
= D о

6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:

8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника

d
= √2S: sin β

Свойства и признаки ромба

Тип утверждения	Фигура	Рисунок	Формулировка
Определение	Ромб		Ромбом называют параллелограмм, у которого все стороны равны
Свойство	Биссектрисы углов диагонали		Если параллелограмм является ромбом, то его диагонали является биссектрисами углов
Признак	Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство	Перпендикулярность диагоналей		Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак	Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Определение: ромб
	Ромбом называют параллелограмм, у которого все стороны равны
Свойство: биссектрисы углов и диагонали
	Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов
Признак: биссектрисы углов и диагонали
	Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Свойство: перпендикулярность диагоналей
	Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак: перпендикулярность диагоналей
	Если у параллелограмма диагонали перпендикулярны, то он является ромбом

Определение: ромб — это прямоугольник, у которого все стороны равны.

ДОКАЗАТЕЛЬСТВО: Если диагонали прямоугольника являются биссектрисами его углов, то прямоугольник является ромбом.

Свойство: если прямоугольник является ромбом, то его диагонали перпендикулярны

Доказательство: если диагональ прямоугольника перпендикулярна, то он является ромбом

Квадрат

Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.

Задача на смекалку от короля. Помогите принцессе Точке ее решить.

Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».

Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.

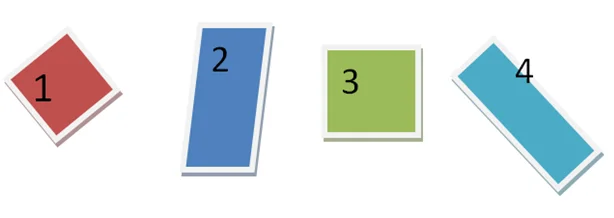
Найдите среди этих прямоугольников квадраты. Запишите их номера.

Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:

Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?

Угол. Виды углов: прямой, тупой, острый

Ребята, а вы знаете, что такое угол? Какие бывают углы?

Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:

Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.

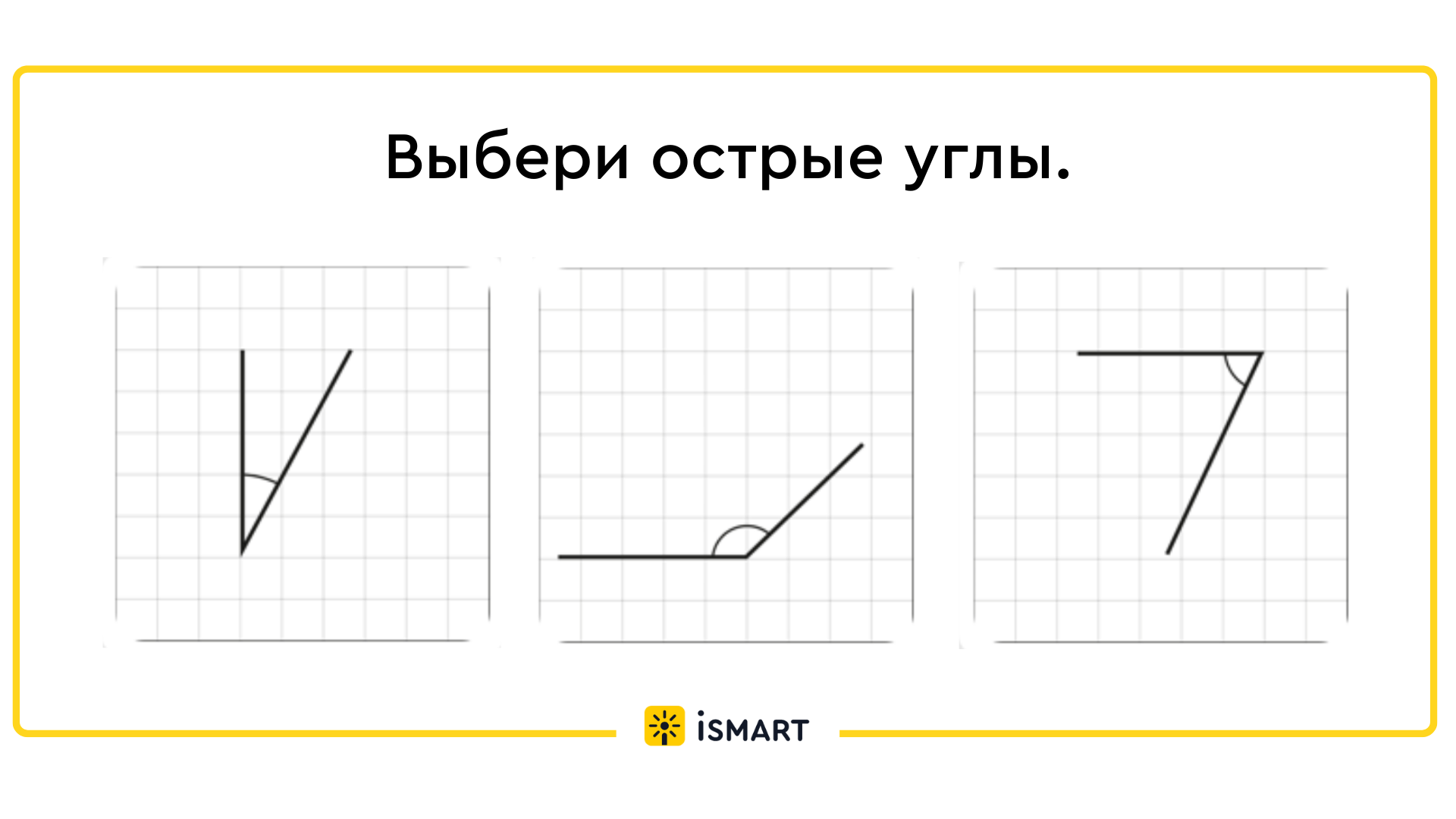
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.

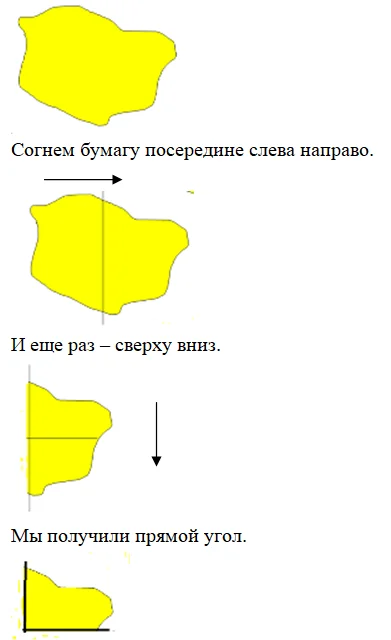
Изготовим модель прямого угла из кусочка бумаги.

Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.

Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.

Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?

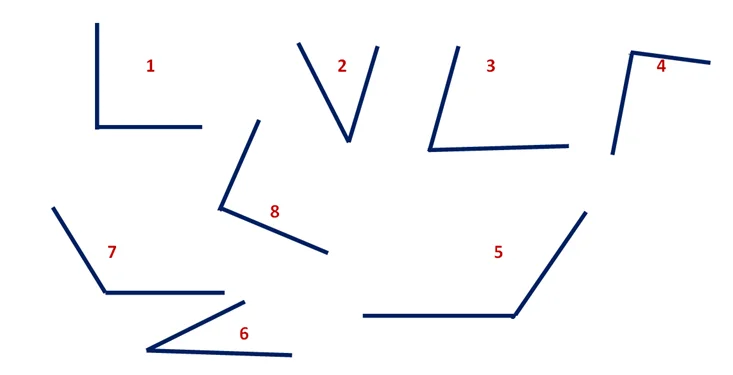
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.

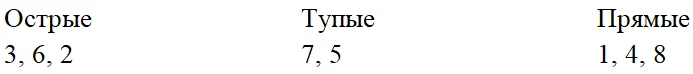
Основные величины

Площадь

Что такое площадь? Это часть плоскости, которая находится внутри фигуры, например, треугольника

Этот термин встречается достаточно часто в задачках и учебниках, поэтому понимать, что он означает — важно. Как находить? Перемножить длину и ширину — так ты получишь, сколько территории находится внутри.

Периметр

Что такое периметр? Это сумма всех длин сторон

Искать достаточно просто и логично, но некоторые формулы для фигур просто облегчают работу, например, квадрат — не нужно отдельно записывать сумму, ведь можно просто узнать, чему равна одна сторона и умножить ее на 4. Такая же схема и с параллелограммом — правда, умножать не на четыре, а боковую и основу на два, но смысл «облегчения» остается таким же.

Аксиомы

• Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
• Через любую точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную данной, и притом только одну.
• Если две прямые параллельны третьей прямой, то эти две прямые параллельны.
• Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
• Любые три прямые имеют не более одной общей точки.
• Через любую точку проходит более одной прямой.
• Через любую точку проходит не менее одной прямой.
• Через любые две точки можно провести прямую.
• Через любые три точки проходит не более одной прямой.
• Через любые три точки проходит не более одной прямой.

Применение прямоугольников в дизайне

Прямоугольники могут быть использованы в дизайне мебели и конструкций, созданных для интерьера. Их прямоугольная форма позволяет легко сочетать их с другими элементами и создавать необычные и функциональные изделия. Прямоугольник может служить основной формой для столов, стульев, шкафов и других предметов мебели. Его применение в дизайне также может быть видно в графике и искусстве, где прямоугольник используется для создания рамок, постеров и других графических элементов.

Прямоугольники имеют много полезных свойств, которые могут быть использованы в дизайне. Например, у прямоугольника есть периметр и площадь, что может быть полезно при создании конструкций и мебели

Также важно учитывать сочетаемость прямоугольников с другими геометрическими фигурами, чтобы создать гармоничный дизайн

Эта геометрическая фигура имеет множество признаков и свойств, которые могут быть применены в дизайне. Например, прямоугольник может иметь одну из сторон равной 18 см

Важно учесть, что прямоугольник может быть создан в разных размерах и пропорциях

Перекрещенные прямоугольники

A скрещенные (самопересекающиеся) четырехугольники состоят из двух противоположных сторон несамопересекающегося четырехугольника вместе с двумя диагоналями. Точно так же скрещенный прямоугольник — это скрещенный четырехугольник, который состоит из двух противоположных сторон прямоугольника вместе с двумя диагоналями. Он имеет то же расположение вершин , что и прямоугольник. Он выглядит как два идентичных треугольника с общей вершиной, но геометрическое пересечение не считается вершиной.

Скрещенный четырехугольник иногда сравнивают с галстуком-бабочкой или бабочкой. Скрученная трехмерная прямоугольная проволочная рамка может принимать форму галстука-бабочки. Перекрещенный прямоугольник иногда называют угловой восьмеркой.

Внутренняя часть скрещенного прямоугольника может иметь плотность многоугольника в каждом треугольнике, равную ± 1, в зависимости от ориентации намотки по часовой стрелке или против часовой стрелки.

Перекрещенный прямоугольник не является равноугольным. Сумма его внутренних углов (два острых и два рефлекса ), как и у любого скрещенного четырехугольника, составляет 720 °.

Прямоугольник и скрещенный прямоугольник являются четырехугольниками. со следующими общими свойствами:

• Противоположные стороны равны по длине.
• Две диагонали равны по длине.
• Он имеет две линии симметрии отражения и симметрии вращения 2-го порядка (на 180 °).

Треугольники

• Сумма углов любого треугольника равна 180° .
• Сторона треугольника меньше суммы двух других сторон данного треугольника. (неравенство треугольника)
• Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
• Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (1 признак равенства треугольников)
• Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. (2 признак равенства треугольников)
• Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (3 признак равенства треугольников)
• Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. (1 признак подобия треугольников)
• Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. (2 признак подобия треугольников)
• Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. (3 признак подобия треугольников)
• Напротив равных углов лежат равные стороны.
• Если два угла треугольника равны, то равны и противолежащие им стороны.
• Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне.
• Площадь треугольника равна полупроизведению двух сторон треугольника на синус угла между ними.
• Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, является медианой (то есть делит основание на две равные части) и высотой (перпендикулярна основанию).
• Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
• В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
• В прямоугольном треугольнике катет, лежащий напротив угла 30° равен половине гипотенузы.
• В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине этой гипотенузы.
• Площадь прямоугольного треугольника меньше произведения его катетов.
• Площадь прямоугольного треугольника равна половине произведения его катетов.
• Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. (теорема косинусов).
• Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
• Стороны треугольника пропорциональны синусам противолежащих углов. (теорема синусов)
• Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
• Один из углов треугольника всегда не превышает 60°.
• Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
• Биссектрисы треугольника пересекаются в центре его вписанной окружности.

Свойства параллелограмма

• Противоположные стороны параллелограмма равны
• Противоположные углы параллелограмма равны
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Точка пересечения диагоналей называется центром симметрии параллелограмма
• Диагональ делит параллелограмм на два равных треугольника
• Сумма углов, прилежащих к одной стороне, равна 180°. (см. формулу ниже)
• Сумма всех углов равна 360°
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей и делятся этой точкой пополам
• Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон (см. формулу ниже)

Свойства прямоугольника

Свойства прямоугольника можно разбить на две группу: свойства параллелограмма и свойства прямоугольника.

Свойства параллелограмма:

• Противоположные стороны попарно равны и параллельны.
• Противоположные углы равны.

Рис. 2. Свойства параллелограмма

Свойства прямоугольника:

• Все углы равны 90 градусам, что вытекает из определения фигуры.
• Диагональ прямоугольника разбивает фигуру на два малых равных прямоугольных треугольника. Это свойство легко доказать. Треугольники будут прямоугольными, так как включают в себя по одному углу в 90 градусов. При этом диагональ будет являться общей стороной, а катеты окажутся равными, так как противоположные стороны параллелограмма попарно равны и параллельны.
• Диагонали прямоугольника равны.

Рис. 3. Луч

Прямоугольники по расположению сторон:

Прямоугольники могут быть разделены по расположению их сторон. В зависимости от этого, выделяют следующие виды:

• Прямоугольник со сторонами, параллельными осям координат. Такой прямоугольник имеет вертикальные и горизонтальные стороны, а его углы равны 90 градусам.
• Прямоугольник со сторонами, не параллельными осям координат. В этом случае углы прямоугольника не равны 90 градусам, а стороны наклонены под определенным углом.
• Квадрат – частный случай прямоугольника, у которого все стороны равны друг другу.
• Прямоугольник со сторонами, перпендикулярными друг другу. В таком прямоугольнике две пары противоположных сторон параллельны и равны между собой.

Независимо от расположения сторон, прямоугольники часто используются в геометрии, строительстве, дизайне и других областях

Они являются важной базовой фигурой и способны применяться в самых разнообразных задачах

Что это такое?

Геометрические фигуры — это основа геометрии. Достаточно логично, не кажется? Но их бездна — а знать приходится абсолютно все, так как они могут быть прописаны в условии без чертежа, а тебе придется гадать, что просят найти составители. Так давай разберемся с основными геометрическими фигурами планиметрии, чтобы хотя бы на простом фактчекинге у тебя не было проблем.

Так, структура будет простая — сначала картинка, потом информация, потом заново. Все понятно? Тогда начинаем!

Квадрат

Думаю, у тебя не возникает особо вопросов в понимании, что такое квадрат, не так ли? Это та геометрическая фигура, которую мы видим с детства — играем с ней, взаимодействуем постоянно. Быстренько пройдемся по свойствам в таком случае: все четыре стороны равны — главное! Противоположные стороны параллельны, сумма углов 360 — это относится ко всем параллелограмм. И еще один факт, который тебе понадобится скорее всего, чтобы быстренько решать тестовые задачки, — диагонали квадрата имеют одинаковые длины, пересекаются под прямым углом и делят друг друга пополам. Это популярно у составителей, например, ЕГЭ, ОГЭ, для проверки базовых знаний геометрии.

Прямоугольник

Тоже популярная геометрическая фигура — прямоугольник. Главные: противоположные стороны равны и параллельны. Это снова идет от параллелограмма — если что, эта фигура и предыдущая — частные случаи его, поэтому есть достаточно много совпадений. Снова у нас будет сумма углов в 360 — у всех замкнутых фигур с четырьмя точками такая характеристика. Диагонали снова равны и делятся пополам точкой пересечения.

Трапеция

Уже подошли к чуть менее известным геометрическим фигурам, если ты только начинаешь изучать геометрию. Один из самых важных фактов — сумма углов, которые прилегают к боковой диагонали, равняется 180. Это поможет тебе достаточно сильно во многих задачках по трапеции.

Ромб — редкий гость в задачках, но знать о нем все-таки необходимо. Главное — высоты равны между собой.

Круг

Как обычно, картинка сверху, чтобы посмотреть, как выглядит чертеж. Один из основных аспектов, которые тебе нужно знать в данной подтеме — это различие круга от окружности. Чем же они отличаются? Смотри, окружность — это замкнутая кривая, где все точки равноудалены от центра. А круг — это геометрическая фигура, которая ограничена окружностью. Именно поэтому нужно знать, чем они отличаются, чтобы не перепутать друг с другом.

Треугольник

Любимый друг абсолютно всех задачек и решений. Многие номера можно решить, даже если ты только знаешь о треугольнике — настолько он хорош. Особенно советуем изучить прямоугольный треугольник — вот, кто попадается настолько часто, что аж страшно становится.

Угол

Все эти пять фигур — это самая первая информация, которую ученики должны изучать в школе на этом предмете. Из них строятся остальные фигуры, понятия, поэтому запомни, как они называются и чем отличаются.

Квадратные, идеальные и другие мозаичные прямоугольники

Прямоугольник, выложенный квадратами, прямоугольниками или треугольниками, называется прямоугольник «квадрат», «прямоугольник» или «треугольник» (или «треугольник») соответственно. Прямоугольник с мозаикой идеален, если плитки подобны и имеют конечное число, и нет двух плиток одинакового размера. Если две такие плитки одинакового размера, плитка неидеальна. В идеальном (или несовершенном) треугольном прямоугольнике треугольники должны быть прямыми треугольниками.

. Прямоугольник имеет соизмеримые стороны тогда и только тогда, когда он может быть выложен конечным числом неравных квадратов. То же самое верно, если плитки — неравные равнобедренные прямоугольные.

мозаики прямоугольников другими плитками, которые привлекли наибольшее внимание, — это совпадающие непрямоугольные полимино, допускающие все вращения и размышления. Есть также мозаики по конгруэнтным полиаболо

Документ без названия

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.

Различают выпуклые и невыпуклые  и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла.

Четырехугольник, у которого угол больше развернутого называется невыпуклым

• Виды четырёхугольников
• Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны; Прямоугольник — четырёхугольник, у которого все углы прямые; Ромб — четырёхугольник, у которого все стороны равны; Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны; Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
• (Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
• Свойства

• Сумма углов четырёхугольника равна 2 π = 360°.
• Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
• Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
• Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
• Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
• Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
• Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
• Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
• Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.

Теорема Вариньона Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника. или сокращённо

Середины сторон произвольного четырёхугольника — вершины параллелограмма

Доказательство  

Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.

Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ проходит внутри четырёхугольника. Тогда площадь треугольника равна , где — высота треугольника , проведённая из вершины . Аналогично, площадь треугольника равна . Тогда площадь всего четырёхугольника равна . Но — это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади ,

1. Теорема Эйлера
2. в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями Следствие: Сумма квадратов длин равна  диагоналей параллелограмма равна сумме квадратов длин его сторон
3. Теорема Птолемея Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
4. Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)

Если a, b, c, d – длины сторон четырёхугольника,  – его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна . В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: ; это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: .