Мягкое знакомство с дополнительным кодом

Литература

1. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2013 года по информатике и ИКТ (проект).
2. Ал.А. Марков, Введение в теорию кодирования. — М.: Наука, 1982.
3. С.В. Яблонский, Введение в дискретную математику. — М.: Наука, 2000.
4. Л.П. Жильцова. Современные проблемы теории кодирования. Учебно-методические материалы по программе повышения квалификации «Информационные технологии и компьютерное моделирование в прикладной математике». — Нижний Новгород: 2007.
5. Л.П. Жильцова, Т.Г. Смирнова. Основы теории графов и теории кодирования в примерах и задачах: Учебное пособие. — Нижний Новгород: Издательство Нижегородского госуниверситета, 2008.

Автор благодарит М.А. Ройтберга за полезные замечания по материалу статьи и Л.Н. Евич за обсуждении вопросов однозначного декодирования на форумеegekp.unoforum.ru

Перевод информации в двоичный код

Основная причина использования двоичной системы счисления в компьютерах связана с электрическими свойствами сигналов. Электрические сигналы в компьютерных системах представляются в виде двух состояний: высокого напряжения (1) и низкого напряжения (0). Использование двух состояний позволяет легко и надежно передавать информацию через провода, чипы и другие компоненты компьютерной системы.

Перевод информации из десятичной системы счисления (основанной на десяти цифрах) в двоичную систему (основанную на двух цифрах) осуществляется по определенным правилам. Каждая цифра десятичной системы заменяется на соответствующий ей набор двоичных цифр. Например, число 8 в десятичной системе будет представлено как 1000 в двоичной системе.

Перевод информации в двоичный код необходим для работы центрального процессора компьютера, который оперирует данными в виде единиц (1) и нулей (0). Центральный процессор выполняет арифметические и логические операции над двоичными данными, что позволяет выполнить сложные вычисления и обрабатывать большие объемы информации.

Применение двоичного кодирования также обеспечивает эффективность работы компьютерных систем и их совместимость. Двоичный код является универсальным и понятным для всех компьютеров и устройств, поэтому информацию, закодированную двоичным способом, можно передавать и обрабатывать на различных платформах.

Виды использования двоичного кодирования

Двоичное кодирование – это процесс представления информации с помощью двух символов: 0 и 1. Это основа для работы компьютерных систем и сетей передачи данных. Двоичный код используется в различных областях, включая электронику, вычислительную технику, передачу данных и телекоммуникации.

1. Цифровая сигнализация

Одним из основных применений двоичного кодирования является цифровая сигнализация. В телекоммуникационных системах информация передается в виде серии двоичных символов, которые представляют звуковые, видео или текстовые данные. Это позволяет передавать информацию в более надежной и эффективной форме.

2. Хранение и обработка данных

В компьютерах и других электронных устройствах двоичное кодирование используется для хранения и обработки данных. Все данные, такие как числа, текст и графика, представляются в компьютерных системах с помощью двоичного кода. Это обеспечивает возможность хранения и обработки большого количества информации в компактной и эффективной форме.

3. Криптография

Двоичное кодирование также находит применение в области криптографии. В криптографии данные шифруются с использованием различных алгоритмов и ключей. Двоичный код используется для представления шифрованных данных и ключей, что обеспечивает безопасность передачи информации и защиту от несанкционированного доступа.

4. Арифметика и логика

Двоичное кодирование является основой для арифметических и логических операций, которые выполняются в компьютерах и электронных устройствах. Числа представляются в двоичной форме, и с их помощью выполняются операции сложения, вычитания, умножения и деления. Также двоичный код используется для логических операций (И, ИЛИ, НЕ) и побитовых операций (И, ИЛИ, исключающее ИЛИ).

5. Программирование

В программировании двоичное кодирование используется для представления инструкций и данных в компьютерных программных системах. Программы и данные хранятся и передаются в двоичном формате, что обеспечивает правильное выполнение команд компьютером. Использование двоичного кодирования позволяет программистам создавать сложные и эффективные программы для различных задач.

6. Цифровая обработка сигналов

Цифровое кодирование и обработка сигналов – это область, связанная с анализом и преобразованием аналоговых сигналов в цифровую форму. Двоичный код используется для представления и обработки аналоговых сигналов, таких как звук, видео или изображение, с целью их сохранения или передачи по сети.

7. Биометрическая идентификация

В биометрической идентификации двоичное кодирование используется для представления биометрических данных, таких как отпечатки пальцев, голосовые сигналы или изображения лиц. Это позволяет сравнивать и идентифицировать людей на основе их уникальных физиологических характеристик.

Все эти области использования двоичного кодирования свидетельствуют о его универсальности и важности для современной технологии и информационных систем. Без двоичного кодирования мы бы не смогли понять, обрабатывать и передавать информацию в цифровом виде

Что такое системы счисления

С давних пор людям нужно было записывать числа. В торговле числа нужны, чтобы знать, сколько товаров есть на складе и сколько денег принесла сделка. Записи о положении небесных тел помогли шумерам составить первый календарь, а календарь, в свою очередь, пригодился, чтобы заранее готовиться к посевным и сбору урожая. Строительные сметы, переписи населения, распределение наследства — числа оказались очень востребованными даже в самых древних государствах.

Так что люди научились записывать числа в незапамятные времена. Небольшие числа легко записывались зарубками или насечками, но если в числе несколько знаков, требуется иная система записи. Эту проблему в разных странах решали по-разному.

Сейчас разные способы записи чисел называются системами счисления.

Систем счисления было придумано довольно много, и даже в наши дни мы используем две системы, возникшие в далёкой древности. Из Древнего Рима к нам пришла римская система счисления, где цифры обозначаются буквами латинского алфавита. За основу римляне взяли количество пальцев на одной руке — 5, и на двух руках — 10. Числа 1, 5 и 10 в римской системе обозначаются буквами I, V и X, и с помощью них можно записать любое число от 1 до 49. Например, VII это 7, а XIX — 19.

От Древних Шумеров мы научились делить дроби на шестьдесят частей. Именно из-за них в нашем часе 60 минут, а в минуте 60 секунд. Шумерская система счисления так и называется — шестидесятеричная. Но, конечно, наиболее привычной выглядит численная запись в системе, которую придумали в Древней Индии. Сейчас ее называют арабской или десятичной системой счисления.

Представление о кодировании информации

Кодированием является преобразование информации в другую (альтернативную) форму. По сути, системы кодирования могут считаться аналогами шифру поимённой подмены, когда каждый единичный блок информационных данных, которые подлежат кодированию, замещаются соответствующим ему шифром. Но имеется и отличие, и оно заключается в присутствии в операции шифрования специальной изменяемой части, именуемой ключом. Такая изменяемая часть для одного и того же пересылаемого сообщения при одном и том же используемом алгоритме, может сформировать разные текстовые форматы шифровки. Когда применяется кодирование вместо шифрования, такой изменяемый компонент просто отсутствует. Как раз по этой причине одно и тоже передаваемое сообщение при выполнении многократного кодирования не изменяет свой формат, а всегда обладает одинаковым видом. Ещё одним отличием кодирования является применение кодовых заменителей для целых слов и даже предложений или совокупности цифр. Замена фрагментов информации, которые подлежат кодированию, кодовыми символами исполняется на основе специальных таблиц (похожих на таблицы шифровальных замен) или вычисляется при помощи алгоритмов или функций для кодировок.

Главными целями информационного кодирования являются следующие задачи:

1. Создание дополнительных преимуществ для хранения, анализа и трансляции информации, поскольку фактически всегда данные в кодовом формате занимают меньший объём памяти и более приспособлены для работы с ними и пересылки их при помощи автоматизированных программных и технических средств.
2. Обеспечение удобного информационного обмена среди объектов.
3. Обеспечение наглядного отображения.
4. Осуществление идентификации субъектов и объектов.
5. Сокрытие доступа к секретным данным.

Существует одноуровневое информационное кодирование и многоуровневое. К примеру, световые сигналы светофора (красный, жёлтый, зелёный) являются одноуровневым кодированием. Многоуровневым кодированием может считаться визуальное отображение фотографии, которое сохранено в виде отдельного файла. Прежде всего, фотография разделяется на совокупность отдельных мелких модулей, именуемых пикселями, то есть все мелкие фрагменты изображения подвергаются кодированию в виде элементарных модулей (элементов). Любой элемент можно представить в виде набора составляющих базовых цветов, а именно, красного, зелёного и синего, имеющих необходимую амплитуду (интенсивность), которая выражена в числовом формате.

Далее числовые совокупности подвергаются перекодированию с целью обеспечить информации большую компактность (например, в форматах jpeg, png и тому подобное). В итоговом результате, сформированные числовые значения трансформируются (перекодируются) в электромагнитные импульсы и транслируются по специальным каналам для коммутации или участкам на носителях информации.

Существуют обратимые и необратимые методы кодирования информации. Когда применяется обратимое кодирование, то закодированные данные всегда могут быть восстановлены без потери информации. При использовании необратимого кодирования отсутствует возможность достоверного восстановления исходной информации.

Неравномерные коды

Пример 3

М	А	Ы	Л	У	пробел	(3)
01	00	1011	100	1010	11

МАМА МЫЛА ЛАМУ → 0100010011011011100001110000011010

Условие Фано. Никакое кодовое слово не совпадает с началом другого кодового слова.

префикснымиУпражнение

1000001101011010001001101101110000 

Пример 4

М	А	Ы	Л	У	пробел	(4)
10	00	1101	001	0101	11

МАМА МЫЛА ЛАМУ → 1000100011101101001001100100100101

постфиксными

Сообщение декодируется однозначно, если для используемого кода выполняется прямое или обратное условие Фано.

• для однозначной декодируемости достаточно выполнение хотя бы одного из двух условий, или прямого, или обратного;
• могут существовать коды, для которых не выполняется ни прямое, ни обратное условие Фано, но они, тем не менее, обеспечивают однозначное декодирование.

Что такое бинарный код и как он работает

Бинарный код — это способ представления информации с помощью двух состояний или значений, обычно обозначаемых как 0 и 1. Он является основой для работы компьютеров и цифровых устройств.

Вся информация в компьютерных системах, таких как текст, изображения, звук или видео, представляется в виде двоичного кода. Каждый символ или элемент информации имеет свою уникальную последовательность из нулей и единиц. Бинарный код используется для передачи, обработки и хранения данных в цифровых системах.

Бинарный код основан на системе счисления с основанием 2. В этой системе каждая позиция числа имеет вес, увеличивающийся в два раза от позиции к позиции слева направо. Самая правая позиция имеет вес 1, следующая — 2, затем 4, 8 и так далее.

Каждая цифра двоичного кода, называемая битом (от англ. binary digit), может быть либо 0, либо 1. Например, число 101 представляет собой комбинацию 1 и 0, где 1 находится на самом правом месте, 0 — в следующей позиции, а еще 1 — в самой левой позиции.

• 1 в двоичной системе равно 1 в десятичной системе
• 10 в двоичной системе равно 2 в десятичной системе
• 11 в двоичной системе равно 3 в десятичной системе
• 100 в двоичной системе равно 4 в десятичной системе
• и так далее…

Комбинация и последовательность битов позволяет представлять и обрабатывать различные типы информации, включая числа, текст, изображения и звук. Например, в ASCII-кодировке каждому символу алфавита и некоторым специальным символам соответствует уникальная последовательность из 7 или 8 битов.

Бинарный код используется компьютерами для выполнения операций, таких как арифметические вычисления, логические операции и управление устройствами. Основываясь на комбинации и последовательности битов, компьютеры могут выполнять сложные задачи и обрабатывать огромные объемы информации.

Таким образом, бинарный код является основой для работы с цифровыми данными и компьютерными системами. Понимание его основных принципов помогает разобраться в работе компьютеров и расшифровывать информацию, хранящуюся и передаваемую в двоичном формате.

Convert Text to Binary

Переводчик с английского на двоичный — Бесплатный онлайн-конвертер текста в двоичный

Наш переводчик с английского на двоичный преобразует обычный текст/английский или ASCII в двоичный код для связи с электронными машинами.

Преобразователь текста в двоичный код — лучший способ преобразовать вашу строку английских букв в двоичный код (0 и 1), чтобы его было легко понять электронными машинами. Текстовая строка на английском языке или ASCII при переводе становится длинной строкой чисел.

Например,

• «hello» в двоичном формате будет 01001000 01100101 01101100 01101100 01101111.
• Заглавная буква «А» будет 01000001.
• Строчная буква «а» будет 01100001.

Когда нам нужно быстро преобразовать английский текст или текст ASCII в двоичный код, лучше всего использовать онлайн-переводчик текста в двоичный код. Этот процесс менее сложен и может быть выполнен в несколько кликов.

Использовать конвертер текста в двоичный код очень просто и требует выполнения нескольких шагов.

• Открыть текст в двоичном формате
• Введите текстовую строку ASCII и выберите тип «Кодировка символов».
• Нажмите кнопку «Конвертировать». Инструмент работает как конвертер текста в двоичный код, где слова точно и без ошибок переводятся в двоичный код.
• Например, введя текст «Пример», вы получите двоичный код «01000101 01111000 01100001 01101101 01110000 01101100 01100101».
• Предположим, вы хотите преобразовать двоичный код в обычный текст/английский или ASCII. Используйте наш двоичный код в текст для двоичного перевода.

Ищете дополнительные средства разработки в DNS Checker? Почему бы вам не попробовать нашу онлайн-программу просмотра JSON, генератор MD5 и калькулятор RAID? Все инструменты первоклассные и бесплатные!

Зачем нужен конвертер текста для преобразования текста в двоичный код?

Все мы знаем, что компьютеры понимают двоичный язык — язык 0 и 1. Двоичный код использовался веками, поэтому он широко используется в наших электронных машинах.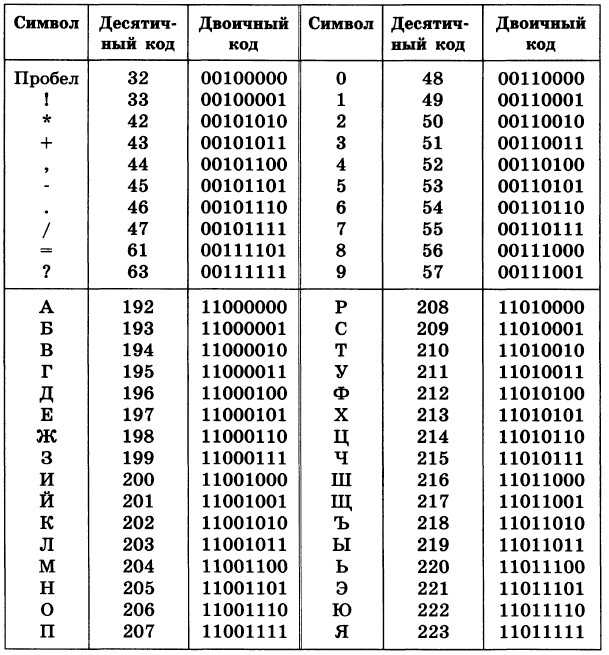

128
64
32
16
8
4
2
1
1

1

Таким образом, заглавная буква «А» в двоичном формате будет 01000001

Как преобразовать число «0» в двоичное?

При первой регистрации в таблице цифре «0» присваивается десятичное число 48. 90

128
64
32
16
8
4
2
1

1
1

Таким образом, число «0» в двоичном формате будет 00110000

Как преобразовать слово «Вау» в двоичное?

Сначала проверьте таблицу и получите десятичное число каждого алфавита.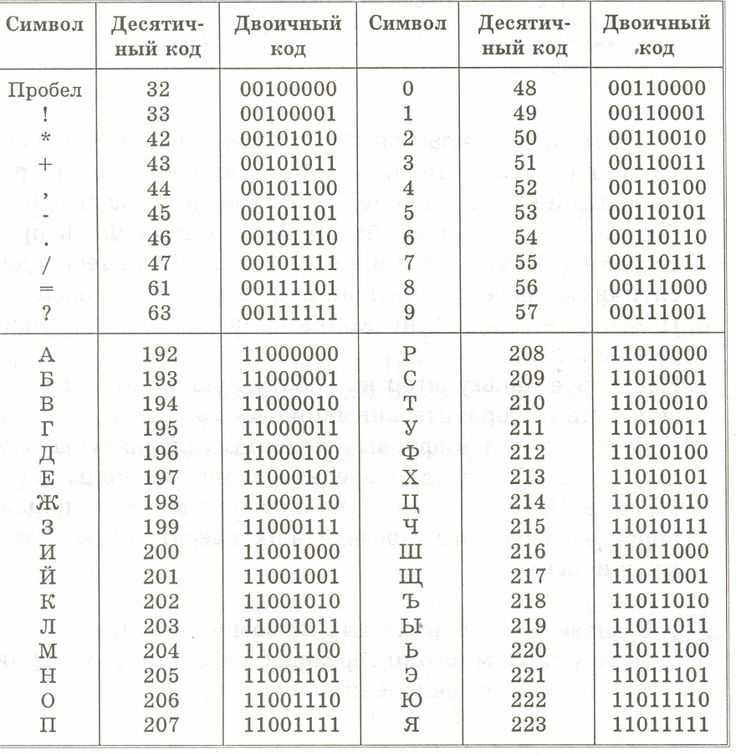

W = 87

o = 111

w = 119

Для W

1

1

1

1

1

Заглавная буква «W» в двоичном коде будет 01010111

Для о

128	64	32	16	8	4	2	1
1	1	1	1	1	1

Маленькая буква «o» в двоичном коде будет 01101111

Для w

128	64	32	16	8	4	2	1
1	1	1	1	1	1

Маленькая буква «о» в двоичном формате будет 01110111

Слово «Вау» в двоичном формате будет

Как преобразовать слово «Любовь» в двоичный код?

Процесс аналогичен описанному выше.

Таким образом, слово «Любовь» в двоичной форме будет

От десятичной системы до двоичной

Десятичная система счисления – это система, которую мы используем в повседневной жизни для обозначения чисел. Она основана на десяти цифрах от 0 до 9 и имеет позиционную структуру.

В то время как десятичная система широко распространена и используется практически повсюду, двоичная система счисления имеет свои уникальные особенности, которые делают ее основой для работы компьютеров.

Двоичная система счисления основана на двух цифрах — 0 и 1. В отличие от десятичной системы, где каждая позиция имеет степень десяти, в двоичной системе каждая позиция имеет степень двойки.

В двоичной системе числа записываются с помощью комбинаций двух символов — 0 и 1. Например, число 14 в двоичной системе записывается как 1110. Каждая цифра в такой записи представляет определенную степень двойки, начиная с 2^0 слева и увеличиваясь на единицу с каждой последующей позицией.

Начиная с 0, двоичные числа могут иметь различную длину. Более того, в двоичной системе счисления нет символов для представления чисел больше 1, поэтому такие числа записываются с использованием комбинаций цифр.

Двоичная система счисления имеет множество важных приложений, особенно в области компьютерных наук. В компьютерах все данные и инструкции представлены в виде двоичных чисел, которые представляют различные состояния электрических сигналов внутри компьютера.

Понимание двоичной системы счисления является важной основой для понимания работы компьютеров и программирования. Оно позволяет нам лучше понять, как данные хранятся и обрабатываются в компьютере, а также как различные операции выполняются с использованием этих данных

Что такое системы счисления

Для записи числа нужен символ. Это может быть как буква «β» (бета) греческого алфавита, так и | (чёрточка). Главное — чтобы символ всегда означал одно и то же количество, имел то же значение. Эти символы назвали цифрами.

Система счисления — это набор цифр, каждая из которых обозначает определённое количество. Системы счисления бывают позиционные и непозиционные. Разберём это на простых примерах.

Возьмём игральные кости и попробуем описать их значения чёрточками:

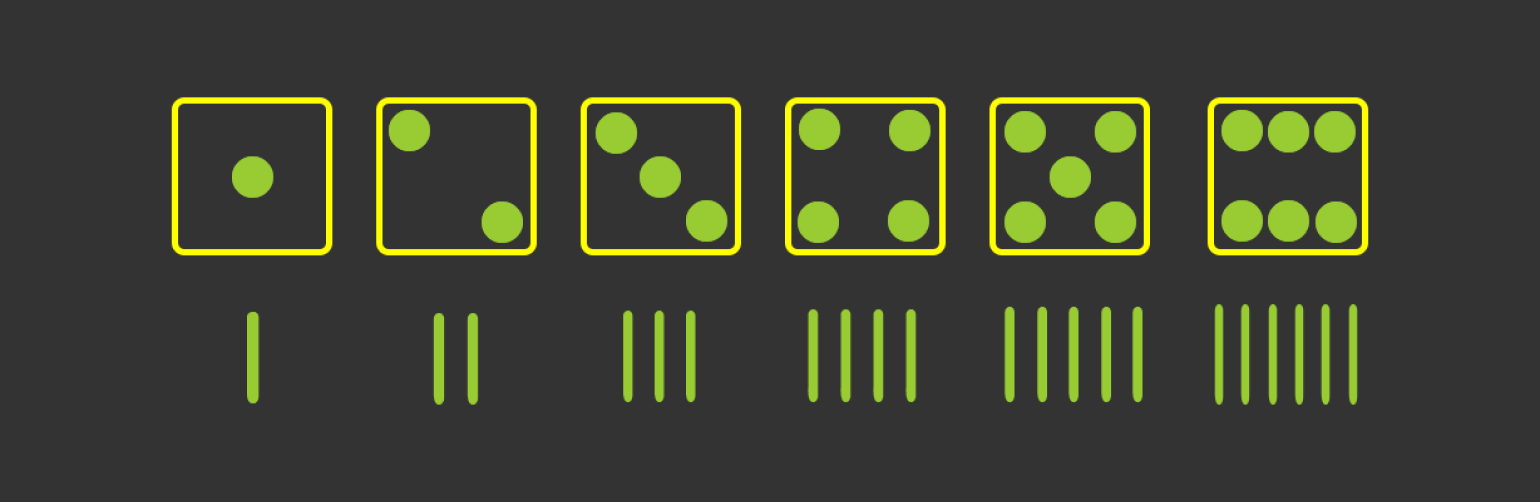
Изображение: Лев Сергеев для Skillbox Media

Перед нами — унарная (единичная) система счисления. Это значит, что в нашем распоряжении есть только один символ. Это не совсем удобно. Поступим по-другому: придумаем для каждого набора чёрточек свои символы. Например:

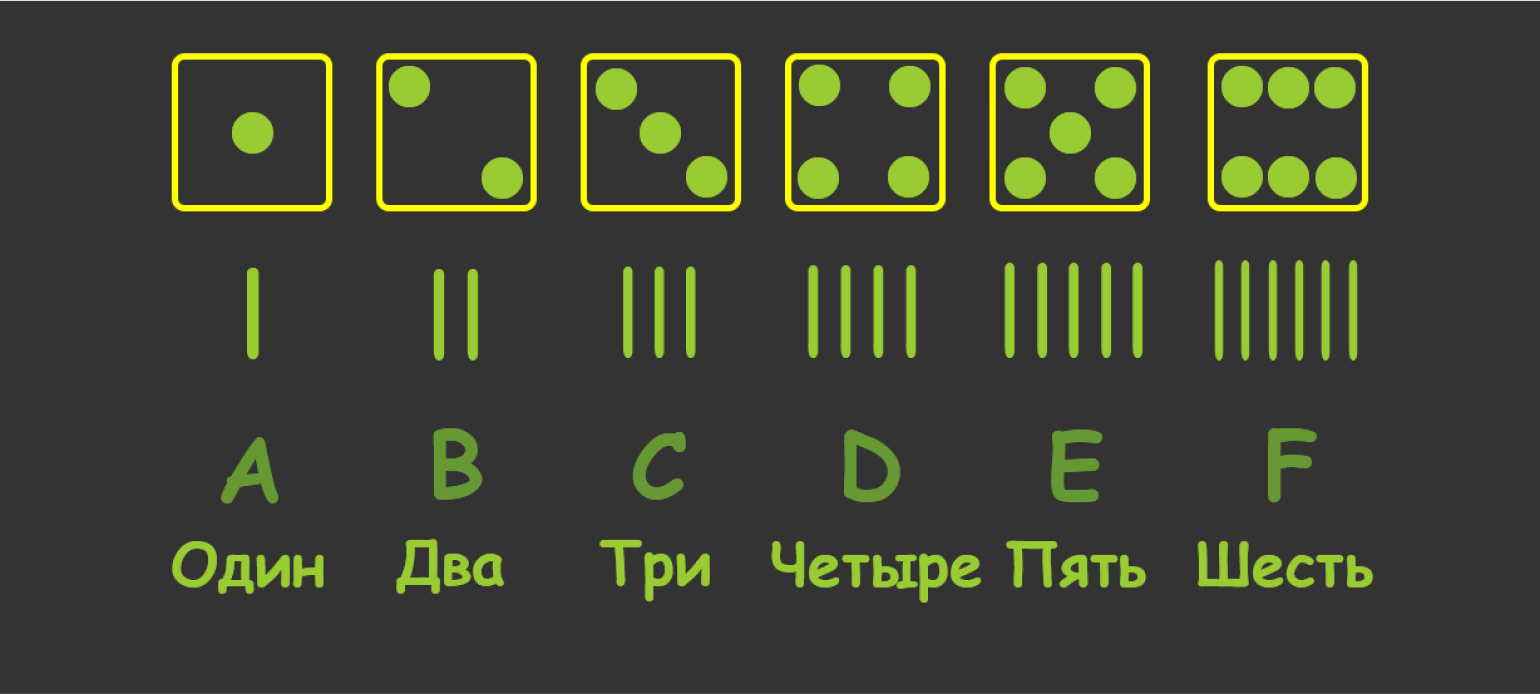
Изображение: Лев Сергеев для Skillbox Media

Символов теперь больше, а запись короче. Такую «кодировку» можно назвать шестеричной системой счисления, в которой 6 цифр:

• A = 1
• B = 2
• C = 3
• D = 4
• E = 5
• F = 6

Уже лучше, но данная система, как и единичная, — непозиционная. Это значит, что положение цифры в записи никак не связано с разрядностью (единицы, десятки, сотни, тысячи и так далее). Классический пример — римская форма записи:

Изображение: Лев Сергеев для Skillbox Media

Такая запись страшно затрудняет не только вычисления, но даже запись чисел, особенно больших, дробных или нерациональных — попытайтесь, например, записать «по-римски» число π (3,1415926535…).

Эту проблему решили позиционные системы счисления, самая популярная из которых — арабская. Разница — налицо. Достаточно посмотреть на запись числа 2023:

Изображение: Лев Сергеев для Skillbox Media

Если в первом случае поменять местами цифры M и X, значение числа не изменится — римляне считывали цифры от больших к меньшим.

Правда, у этого правила была пара исключений. Для удобства записи четвёрку записывали как IV, а девятку — как IX. Но в целом римская нумерация была непозиционной — точно так же, как древнеегипетская, греческая, вавилонская и прочие ветхозаветные.

А вот во втором случае, переставив цифры, мы получим совершенно разные результаты: 0223, 2320 и так далее.

Позиционные системы счисления имеют разряды. Их мы и меняли местами в примере выше. Разряд не может вмещать в себя число меньше или больше, чем основание системы. Основание — это количество цифр в системе счисления.

Изображение: Лев Сергеев для Skillbox Media

Пример позиционных систем:

Какие преимущества предоставляет двоичная система кодирования

Двоичная система кодирования — это способ представления информации с помощью двух состояний, которыми обладают электронные устройства. Она является основой для работы компьютеров и многих других технологий. Преимущества, которые предоставляет двоичная система кодирования, заключаются в ее простоте, надежности и универсальности.

Простота и надежность: В двоичной системе кодирования используются всего два символа — 0 и 1, что делает эту систему простой в понимании и реализации. Наличие только двух состояний позволяет легко определить, является ли сигнал высоким (1) или низким (0). Благодаря этому, двоичная система кодирования обеспечивает надежную передачу и хранение информации.
Универсальность: Двоичная система кодирования является универсальной и может быть использована для представления различных типов информации. Она применяется в компьютерах для представления чисел, текста, аудио-, видеоданных и т.д. Благодаря своей универсальности, двоичная система кодирования может работать с любыми типами данных.
Простота схем сравнения и логических операций: В двоичной системе кодирования сравнение и выполнение логических операций производятся очень просто. Простота этих операций облегчает разработку и реализацию электронных устройств, таких как процессоры и логические вентили.
Эффективность хранения и передачи информации: Двоичная система кодирования позволяет эффективно хранить и передавать информацию. Все данные в компьютере хранятся и передаются в виде двоичных чисел, что позволяет минимизировать объемы памяти и битовых потоков

Это особенно важно при работе с большими объемами информации, например, при передаче видео или аудио данных через интернет.
Упрощение устройства и процессора: Двоичная система кодирования значительно упрощает процессор и устройства, так как все операции в компьютере производятся на двоичном уровне. Это позволяет предотвратить ошибки и упрощает процесс разработки и отладки программ.

В целом, двоичная система кодирования обеспечивает надежность, эффективность и универсальность при представлении информации в компьютерах и электронных устройствах. Она является основой для функционирования современных технологий и играет важную роль в различных сферах человеческой деятельности.

Применение бинарного кода в современных технологиях

Бинарный код, представляющий информацию в виде последовательности единиц и нулей, является основой современных технологий и используется во множестве сфер жизни.

Компьютеры и вычислительная техника:

• Бинарный код является естественным языком для компьютеров и используется для представления и обработки информации. Все данные в компьютере, включая тексты, изображения и звук, хранятся и передаются в виде бинарного кода.
• Процессоры компьютеров работают с бинарным кодом, выполняя арифметические и логические операции.

Цифровая передача данных:

• При передаче данных по сети или через Интернет, они преобразуются в бинарный код, чтобы могли быть переданы по каналам связи, используя различные протоколы.
• Бинарный код позволяет надежно передавать и восстанавливать данные, так как единицы и нули легко определить и интерпретировать.

Криптография:

• Бинарный код используется в криптографии для шифрования и расшифровки данных. Различные алгоритмы шифрования преобразуют данные в бинарный код и обратно с использованием специальных ключей.
• Шифрование в бинарном коде обеспечивает безопасность передачи и хранения информации, так как расшифровать данные без знания правильного ключа практически невозможно.

Цифровая обработка сигналов:

• Бинарный код используется в современных аудио- и видеоустройствах для обработки и воспроизведения звука и изображений.
• Сигналы звука и видео представляются в виде бинарного кода, что позволяет устройствам точно воспроизводить и обрабатывать звук и изображение с высокой степенью точности.

Интернет вещей (IoT):

• Бинарный код используется в устройствах Интернета вещей для обмена данными с другими устройствами и сетями.
• Устройства IoT, такие как смартфоны, датчики, умные дома и автомобили, используют бинарный код для отправки и получения информации, контроля и взаимодействия с другими устройствами.

Машинное обучение и искусственный интеллект:

• Бинарный код играет ключевую роль в алгоритмах и моделях машинного обучения и искусственного интеллекта.
• Данные, используемые для тренировки и обучения моделей, представляются в виде бинарного кода, чтобы компьютер мог анализировать и обрабатывать их.

Применение бинарного кода в современных технологиях широко распространено и охватывает множество сфер. Он является основой для передачи, хранения, обработки и анализа информации, обеспечивая надежность и эффективность работы устройств и систем.

Шестнадцатеричная система счисления

Мы знаем, что компьютер использует числа для представления любой информации. Например, цвета хранятся в виде трёх чисел — яркости красной, зелёной и синей компонентов цвета. На каждый компонент отводится восемь двоичных позиций, поэтому максимальная яркость компонента равна 11111111₂ или 255. Цвет целиком описывается большим 24-х разрядным двоичным числом, например, 11111010 10000000 01110010. Это цвет Salmon из таблицы цветов HTML, он же лососевый цвет.

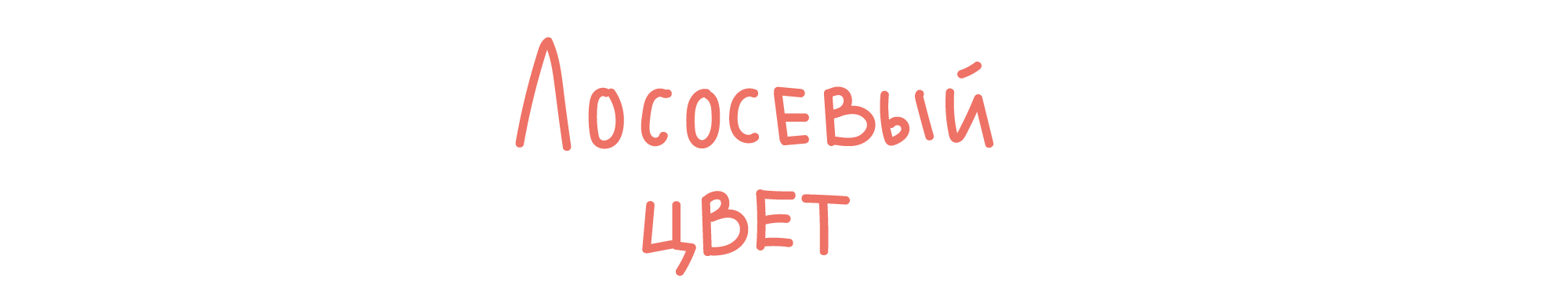
Старшие восемь позиций отводятся для хранения красного компонента, средние восемь — зелёного, и младшие восемь — синего. Мы видим, что такая запись очень громоздка и неудобна.

Кажется, что цвет удобнее записать как десятичное число 16416882. Хотя оно занимает меньше места, по нему трудно понять, какова яркость каждого компонента.

Чтобы записывать большие двоичные числа, программисты придумали использовать шестнадцатеричную систему счисления:

• В десятичной системе десять цифр, а в шестнадцатеричной — шестнадцать
• В десятичной системе соседние позиции отличаются в десять раз, а в шестнадцатеричной — в шестнадцать раз

Как и в случае с двоичной системой, цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 заимствуются из десятичной системы. Но в данном случае этих цифр не хватает: нужно ещё шесть. Их в шестнадцатеричной системе принято обозначать первыми буквами английского алфавита:

Основание 16	Основание 10	Основание 2
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	8	1000
9	9	1001
A	10	1010
B	11	1011
C	12	1100
D	13	1101
E	14	1110
F	15	1111

Шестнадцатеричная система счисления хороша тем, что группа из четырёх двоичных цифр кодируется одной шестнадцатеричной цифрой. Таким образом, лососевый цвет выглядит как:

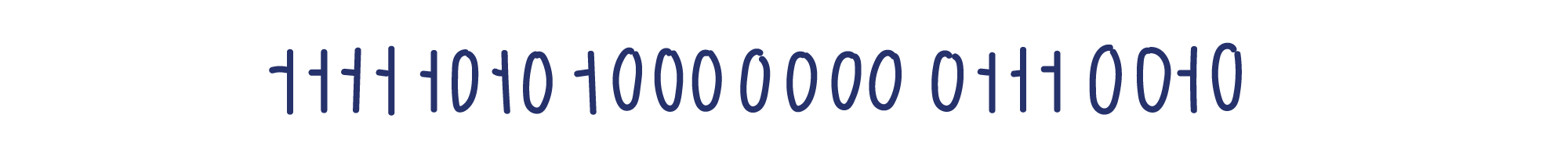
В шестнадцатеричной системе счисления он записывается так:

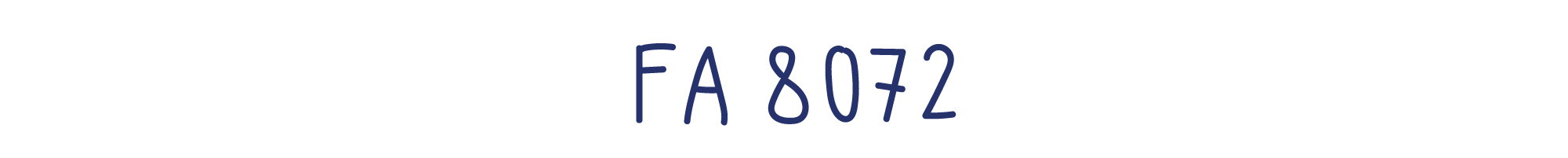
Вначале трудно понять, каков порядок у шестнадцатеричного числа FA. Как и в случае с двоичными числами, программисты обычно помнят порядки круглых шестнадцатеричных чисел. Но можно не запоминать, а подглядывать в эту таблицу:

Шестнадцатеричное число	Десятичное число
1016	16
2016	32
3016	48
4016	64
5016	80
6016	96
7016	112
8016	128
9016	144
A016	160
B016	176
C016	192
D016	208
E016	224
F016	240
10016	256
100016	4 096
1 000016	65 536
10 000016	1 048 576
100 000016	16 777 216
1000 000016	268 435 456
1 0000 000016	4 294 967 296

Чтобы переводить числа из десятичной системы в шестнадцатеричную и обратно, двоичное представление можно использовать как промежуточное. Часто это самый простой способ: двоичное и шестнадцатеричное представления без труда переводятся друг в друга.

Большой информационный объем

Двоичный код представляет информацию с помощью двух символов – 0 и 1, которые соответствуют отключенному и включенному состоянию элементов электронных устройств. Благодаря использованию двоичного кода, можно кодировать и передавать информацию из различных источников, таких как компьютеры, сотовые телефоны, интернет и т.д.

Большой информационный объем требует эффективных методов сжатия и хранения данных. Одним из таких методов является кодирование Хаффмана, который позволяет сократить количество бит, необходимых для хранения информации. Также существуют различные алгоритмы сжатия данных, которые помогают упаковать большой объем информации в более компактный формат.

При передаче большого информационного объема возникает проблема скорости передачи данных. Для увеличения скорости передачи и минимизации ошибок используются различные методы, такие как многопоточная передача данных, использование оптических кабелей и беспроводные технологии связи.

С учетом растущего информационного объема, разработчики постоянно усовершенствуют методы хранения и передачи информации. Большой информационный объем требует использования эффективных алгоритмов сжатия, методов передачи данных и современных технологий связи.