Кратные интегралы

Введение

В рамках общей тенденции к строгости в математике в 19 веке были предприняты попытки поставить интегральное исчисление на прочную основу. Интеграл Римана , предложенный Бернхардом Риманом ( 1826–1866 ) , представляет собой в значительной степени успешную попытку обеспечить такую ​​основу для интеграла. Определение Римана начинается с построения последовательности легко вычислимых интегралов, которые сходятся к интегралу данной функции: это определение дает ожидаемый ответ для многих уже решенных проблем и оказалось полезным во многих других задачах.

Однако интегрирование по Риману плохо справляется с ограничениями последовательностей функций, что затрудняет анализ этих процессов на пределе. Эти пределы имеют первостепенное значение, например, при изучении рядов Фурье, преобразований Фурье и в других областях. Интеграл Лебега лучше всего подходит для описания того, как и когда можно выполнить предельную операцию под знаком интеграла. Фактически, определение Лебега рассматривает другой класс легко вычислимых интегралов, чем определение Римана, и это основная причина, по которой интеграл Лебега ведет себя лучше.

Определение Лебега также позволяет вычислять интегралы для более широкого класса функций. Например, функция Дирихле , равная 0, если ее аргумент иррационален , и 1 в противном случае, имеет интеграл Лебега, но не имеет интеграла Римана.

Построение интеграла Лебега основано на теории меры . Первоначально теория меры была создана для детального анализа понятия длины подмножеств реальной линии и, в более общем смысле, площадей и объемов подмножеств евклидовых пространств . Как показали более поздние разработки в теории множеств , которая также включает понятие неизмеримого множества , фактически невозможно назначить длину всем подмножествам таким образом, чтобы сохранить определенные свойства естественной аддитивности и трансляционной инвариантности. Это говорит о том, что выбор соответствующего класса подмножеств, называемых измеримыми , является важным предварительным условием.

Другие математические символы

В математике существует множество символов, которые используются для обозначения различных математических понятий. Помимо знака интеграла с кружочком по середине, который обозначает интегрирование, есть и другие интересные символы.

Один из таких символов — знак бесконечности (∞). Он используется для обозначения бесконечно больших и бесконечно малых величин. Знак бесконечности состоит из изогнутой горизонтальной линии, похожей на число 8, и обычно располагается на границе угла горизонтальной и вертикальной линий.

Ещё один символ — знак равно (~). Он обозначает приближенное равенство между двумя величинами. Знак равно состоит из знака равенства (=) и тильды (~), которая указывает на приближенность значения.

Также в математике нередко используется греческий алфавит. Например, символ α (альфа) обозначает угол, символ β (бета) обозначает угол, и так далее. Греческий алфавит используется для обозначения различных математических переменных и констант.

В таблице приведены некоторые примеры математических символов:

Символ	Обозначение	Описание
∞	Знак бесконечности	Обозначает бесконечно большие и бесконечно малые величины
~	Знак равно	Обозначает приближенное равенство
α	Альфа	Обозначает угол
β	Бета	Обозначает угол

Это лишь некоторые из множества символов, которые используются в математике

Знание и понимание этих символов является важной частью математической грамотности и позволяет более точно и наглядно выражать математические понятия

Сравнение символа интеграла с другими знаками

В математике символ интеграла с кружочком по середине ( ∫ ) обозначает интеграл функции. Он является одним из основных символов математических формул и широко используется в анализе и вычислительной математике.

Символ интеграла с кружочком по середине имеет несколько особенностей, которые делают его уникальным:

1. Форма символа: символ интеграла напоминает знак «S», однако его верхняя и нижняя границы выглядят следующим образом: над главной линией указывается верхняя граница интегрирования, а под ней — нижняя граница. Такая форма символа интеграла отличает его от других математических знаков.
2. Применение: символ интеграла используется для обозначения операции интегрирования — нахождения площади под графиком функции. Применение этого символа связано с понятием определенного и неопределенного интеграла.
3. Границы интегрирования: символ интеграла указывает на интервал, на котором происходит интегрирование. Верхняя и нижняя границы иногда имеют специальные значения или могут быть переменными.

Сравнение символа интеграла с другими знаками позволяет увидеть его отличительные особенности:

Символ	Значение	Использование
∫	Интеграл функции	Используется для интегрирования и нахождения площади под графиком функции
+	Сложение чисел	Обозначает операцию сложения между двумя или более числами
—	Вычитание чисел	Обозначает операцию вычитания одного числа из другого
*	Умножение чисел	Обозначает операцию умножения двух или более чисел
Деление чисел	Обозначает операцию деления числа на другое число

Таким образом, символ интеграла с кружочком по середине отличается от других знаков математики своей формой и применением. Он является важным инструментом в анализе и вычислительной математике, и его использование позволяет решать различные задачи, связанные с нахождением площадей и вычислением интегралов функций.

Использование в вычислительной математике

Символ интеграла с кружочком по середине, также известный как знак интеграла или знак интегрирования, широко используется в вычислительной математике.

Он используется для обозначения процесса интегрирования, которое является одним из фундаментальных понятий в математике. Интеграл позволяет находить площадь под кривой или выполнять другие операции с функциями.

Символ	Описание
∫	Знак интеграла

В вычислительной математике интегралы используются для решения различных задач, таких как:

• Нахождение площади под кривыми;
• Вычисление определенных и неопределенных интегралов;
• Решение дифференциальных уравнений;
• Определение вероятности события;
• Аппроксимация функций и оценка ошибок.

Знание и умение использовать символ интеграла позволяет специалистам в области вычислительной математики эффективно решать сложные задачи, связанные с анализом и обработкой данных.

Возможные сложности при работе с интегралом с кружочком

При работе со специальным символом кружочка, который используется для обозначения интеграла, могут возникнуть некоторые сложности и недоразумения. Рассмотрим основные из них:

Неспособность правильно нарисовать символ кружочка.
Для обозначения интеграла с кружочком используется символ ∮ (Unicode: U+223E). Некоторые программы и редакторы могут не поддерживать этот символ, поэтому его отображение может быть некорректным. В таком случае можно использовать замену на другой символ или обозначение словами (например, «интеграл по контуру»).

Непонимание значения символа кружочка.
Символ кружочка используется для обозначения интеграла по замкнутому контуру. Это означает, что интеграл вычисляется вдоль замкнутого пути

Не все студенты могут правильно понять эту концепцию и корректно применить ее при решении задач.

Сложности с выбором подходящего контура.
При работе с интегралом с кружочком важно выбрать подходящий контур, вдоль которого будет происходить интегрирование. Неправильный выбор контура может привести к некорректным результатам или даже к невозможности провести вычисления

Для решения этой проблемы необходимо хорошо понимать геометрию и свойства объекта, по которому производится интегрирование.

Сложности с вычислением интеграла вдоль контура.
Интеграл с кружочком требует вычисления интеграла вдоль контура, что может быть более сложным, чем обычное интегрирование. Здесь может потребоваться использование специальных методов, таких как вычеты или формула Коши. В случае недостаточных знаний и навыков, вычисление интеграла может быть затруднительным.

В целом, работа с интегралом с кружочком требует хорошего понимания теоретической базы и умения применять ее на практике. Однако, с достаточной подготовкой и практикой, эти сложности могут быть преодолены, позволяя более глубоко изучить и применить интегралы в различных областях математики и физики.

Интеграл Лебега и интеграл Римана

Интеграл Лебега является обобщением интеграла Римана, который исторически является первым строгим определением, которое было сформулировано для интеграла по интервалу, и чтобы показать его связь, необходимо использовать класс непрерывных функций с компактным носителем , для такой, как интеграл Римана, всегда существует. Пусть и — две непрерывные функции с компактным носителем на . Их расстояние можно определить следующим образом:

Оснащенное функцией расстояния пространство непрерывных функций с компактным носителем является метрическим пространством . Пополнением этого метрического пространства является множество интегрируемых функций по Лебегу. В литературе есть несколько других операторов интегрирования, однако они менее распространены, чем операторы Римана и Лебега.

Интуитивная интерпретация

Интеграл Римана (синий) и интеграл Лебега (красный)

Чтобы наглядно показать разницу между подходами Римана-Дарбу и Лебега, можно представить вычисление интеграла как сумму площадей элементарных множеств. Подход Римана-Дарбу делит график функции на вертикальные участки и вычисляет площадь каждого участка путем умножения значения функции на ширину самого участка. Таким образом, значение интеграла определяется суммой всех площадей вертикальных сечений в пределе, когда их число бесконечно.

Подход Лебега, с другой стороны, предусматривает подразделение графика на горизонтальные участки, также известные как кривые уровня , и каждый из них связан с индикаторной функцией. Сумму всех площадей можно улучшить, добавив кривые промежуточного уровня, уменьшив вдвое разницу между высотами последовательных секций и затем пересчитав сумму. Интеграл Лебега является пределом этого процесса.

Эквивалентный вышеизложенному способ выражения интеграла Лебега получается путем определения:

где он положителен, а интеграл справа является интегралом Римана.

Ограничения интеграла Римана

С появлением рядов Фурье исторически возникало множество аналитических задач, связанных с интегралами, удовлетворительное решение которых требовало перестановки бесконечных сумм функций и знаков интеграла. Однако условия, при которых интегралы:

А также

равны, оказались весьма трудноуловимыми в римановой структуре, так как есть трудности, связанные с предельным переходом под знаком интеграла.

Монотонная сходимость

Поскольку индикаторная функция на рациональных числах не интегрируема по Риману, теорема о монотонной сходимости не выполняется. Действительно, пусть — перечисление всех рациональных чисел в и будет:

Пусть также будет:

Функция равна нулю везде, кроме конечного числа точек, поэтому ее интеграл Римана равен нулю. Последовательность также явно неотрицательна и монотонно возрастает к , что не является интегрируемым по Риману.

Вместо этого функция интегрируема по Лебегу на , будучи функцией, указывающей на рациональные числа. Итак, по определению:

так как он счетный.

Неограниченные диапазоны

Интеграл Римана можно применять только к функциям, определенным на ограниченном интервале. Самое простое расширение состоит в том, чтобы определить:

всякий раз, когда существует предел. Однако это нарушает свойство инвариантности для сдвигов: если и равны нулю вне некоторого интервала и интегрируемы по Риману, а если для некоторого , то интеграл от равен интегралу от . При таком определении несобственного интеграла , часто называемого несобственным главным значением Коши над нулем, функции и являются переводами друг друга, но их несобственные интегралы различны:

Аксиоматическое определение вероятности

Аксиома, имеющая большое значение в теории вероятностей, утверждает, что счетное объединение событий должно быть событием. Если мы попытаемся определить вероятность подмножества интервала как интеграл Римана характеристической функции множества :

мы имеем, что каждое рациональное число между 0 и 1 имеет нулевую вероятность, но их объединение не является событием, поскольку оно не является интегрируемым множеством по Риману, и поэтому ему невозможно приписать вероятность. С интегралом Лебега эта проблема не возникает, и можно дать совершенно последовательное аксиоматическое понятие вероятности.

Криволинейный интеграл

Пусть функция непрерывна в каждой точке дуги . Если разбить эту дугу произвольным способом на частичных дуг длиною выбрать на каждой из них по одной произвольной точке вычислить значения функции в этих точках и составить сумму

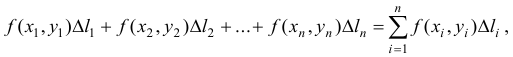
то она называется интегральной суммой функции по дуге .

Криволинейным интегралом первого рода от функции , взятым по плоской кривой , называется предел интегральной суммы при стремлении к нулю наибольшей по длине элементарной ячейки если этот предел существует и не зависит от способа дробления кривой на элементарные ячейки и выбора точек в них.

В прямоугольных координатах элемент дуги .

Если кривая задана параметрическими уравнениями , то

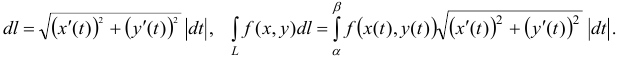
Если кривая задана уравнением , то

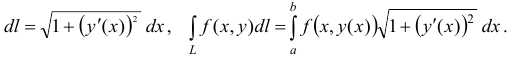
Если кривая задана уравнением , то

Физический смысл криволинейного интеграла первого рода. Масса линии с линейной плотностью определяется по формуле .

Свойства криволинейного интеграла первого рода

1. При изменении направления интегрирования криволинейный интеграл первого рода не изменяет своего знака, т. е. , где — кривая , пробегаемая в заданном направлении, — кривая , пробегаемая в противоположном направлении.
2. Если кривая с помощью некоторой точки разбита на части: , то

Криволинейным интегралом второго рода от пары функций и , взятым по кривой , понимается интеграл . Если кривая задана параметрическими уравнениями , то

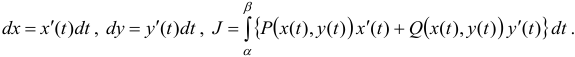
Если кривая задана уравнением , то

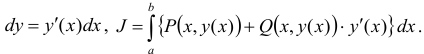
Свойства криволинейного интеграла второго рода

1. При изменении направления интегрирования криволинейный интеграл второго рода изменяет свой знак, т. е. .
2. Если кривая с помощью некоторой точки разбита на части: , то .

Циркуляцией называется криволинейный интеграл по замкнутой плоской линии . При положительном направлении ее обхода (против движения часовой стрелки) обозначается , а при отрицательном направлении обхода обозначается .

Обычно криволинейный интеграл зависит от линии интегрирования. Взятый вдоль разных линий, соединяющих точки и , он будет иметь различные значения. Если же в некоторой области выражение является полным дифференциалом некоторой функции , то криволинейный интеграл не зависит от линии интегрирования, соединяющей точки и , а взятый по любой замкнутой линии, пролегающей в области , равен нулю.

Выражение будет полным дифференциалом функции в некоторой области , если и если непрерывны в этой области.

Полный дифференциал некоторой функции с помощью криволинейного интеграла вдоль ломаной находят по формуле

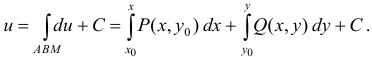
Полный дифференциал некоторой функции с помощью криволинейного интеграла вдоль ломаной находят по формуле

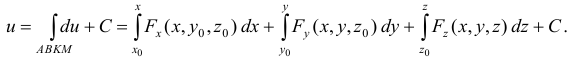
С помощью криволинейных интегралов вычисляются следующие величины:

1) Длина дуги плоской или пространственной линии .

2) Площадь фигуры, расположенной в плоскости и ограниченной замкнутой линией

3) Масса материальной дуги с линейной плотностью вещества в точке дуги .

4) Координаты центра тяжести дуги

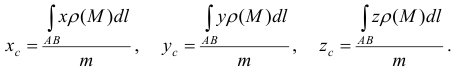
5) Работа , совершаемая силой , действующей на точку при перемещении ее по дуге ,

Формула Грина . Устанавливает связь между двойным интегралом по некоторой плоской области и криволинейным интегралом по границе этой области.

Пример №1

Вычислить криволинейный интеграл, сделать чертеж:

а) вдоль дуги параболы от точки до точки .

б) по дуге эллипса обходя ее против хода часовой стрелки от точки до точки .

Решение:

а) Преобразуем криволинейный интеграл в определенный интеграл с переменной : . Пределы интегрирования определяем из рис. 10: . Вычислим интеграл :

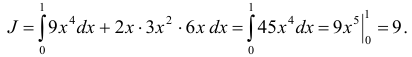
Ответ: .

б) Найдем значение параметра в точках и (рис. 11):

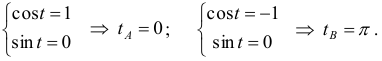
Преобразуем криволинейный интеграл в определенный с переменной , затем вычислим его: ;

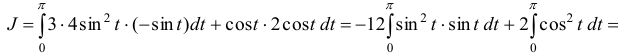
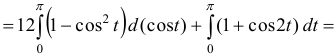
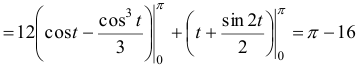
Ответ: .

Пример №2

Проверить, является ли заданное выражение полным дифференциалом некоторой функции , в случае положительного ответа найти с помощью криволинейного интеграла.

Решение:

Обозначим коэффициенты при дифференциалах , и найдем и . Так как и , непрерывны во всей области, за исключением и , то заданное выражение является полным дифференциалом некоторой функции .

Найдем эту функцию:

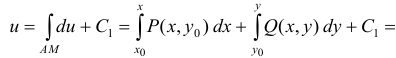
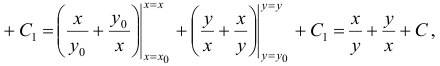
где

Область определения функции совпадает с и .

Ответ: .

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Двойной интеграл

Тройной интеграл

Векторный анализ: основные понятия и пример с решением

Ряды в высшей математике

Несобственный интеграл с бесконечным пределом ами интегрирования

\[

\int_{a}^{\infty} f(x) \, dx

\]

или

\[

\int_{-\infty}^{b} f(x) \, dx

\]

или

\[

\int_{-\infty}^{\infty} f(x) \, dx

\]

В этом случае, для вычисления значений таких интегралов используются различные методы и приемы.

Один из эффективных методов вычисления несобственного интеграла с бесконечным пределом – это модифицировать интеграл, чтобы снизить его до встречаемости в пределах ограниченного промежутка. Затем, используя интегралы с ограниченными пределами, полученные значения суммируются или вычитаются, в зависимости от рода интеграла.

Например, несмотря на то что пределы интегрирования равны бесконечности, определенная площадь внутри графика функции может быть конечной.

Площадь фигуры, ограниченной графиком функции, $Ox$, и прямыми $x = a$, $x = b$ может быть найдена следующим образом:

\[

\int_{a}^{b} f(x) \, dx

\]

Если же одна из сторон фигуры расположена на бесконечности, то для определения площади фигуры необходимо разделить ее на две элементарных фигуры и вычислить площадь каждой из них отдельно.

Несобственные интегралы также могут быть вычислены методом замены переменной или методом интегрирования по частям.

Однако, для решения несобственных интегралов с бесконечными пределами, чаще всего применяют метод обхода.

Сразу следует уточнить, что значения несобственного интеграла могут быть равными как числам, так и $\infty$.

Традиционно при обходе предельных значений несобственного интеграла, используют так называемый «знак с плюсом» или двумя значками «+».

Несобственный интеграл с бесконечным пределом интегрирования может быть модифицирован до равенства следующим образом:

\[

\int_{a}^{\infty} f(x) \, dx = \lim_{x\to\infty} \left( \int_{a}^{x} f(x) \, dx

ight)

\]

или

\[

\int_{-\infty}^{b} f(x) \, dx = \lim_{x\to-\infty} \left( \int_{x}^{b} f(x) \, dx

ight)

\]

Используя полученное равенство, самостоятельно задач естественных и технических наук легко решать даже устно.

Важно также помнить, что для установления равенства несобственного интеграла с бесконечным пределом интегрирования, систематически используется метод ньютона-лейбница, что в свою очередь основано на принципиально новом подходе. Заметим также, что некоторые несобственные интегралы совпадают с другими интегралами, которые стали известны в математике достаточно давно и легко вычисляются с использованием табличных или других методов

Заметим также, что некоторые несобственные интегралы совпадают с другими интегралами, которые стали известны в математике достаточно давно и легко вычисляются с использованием табличных или других методов.

Содержание интегралов и их значения часто определяются степенями и корнями элементарных функций. Например, логарифмы, экспоненциальные, тригонометрические, логистические и подобные им функции.

Значения несобственного интеграла, как правило, находятся в нижнем его пределе, а также в знаменателе дроби и внутри корней, что дает хорошую простоту и точность расчетов.

В этой связи, при вычислении несобственных интегралов снова и снова сталкиваются с некими особыми значениями, которые воспринимаемы макронами, записываемыми в стиле LaTeX.

Также, необходимо быть внимательным при использовании латексного кода, чтобы не допустить опечаток и грамматических ошибок.

Примечание: Для предельных значений интеграла с бесконечным пределом интегрирования достаточно часто используются формулы интегралов, определяющие нижний предел значения несобственных интегралов. Кроме того, интеграл с бесконечным пределом интегрирования может быть решен совместно с другими интегралами, что обеспечивает еще больше вариативности при вычислении данных интегралов.

Свойства интеграла Лебега от простых функций со счетным числом значений

1. $$\int\limits_{X} cf(x) d \mu = c\int\limits_{X} f(x) d \mu~~\forall c \in \mathbb{R}$$.

2. $$\int\limits_{X} f(x) \pm g(x) d \mu = \int\limits_{X} f(x) d \mu \pm \int\limits_{X} g(x) d \mu~~\forall f(x), g(x)$$ — простые функции со счетным числом значений.

Следствие. Интеграл от линейной комбинации функций равен линейной комбинации интегралов от этих функций с теми же коэффициентами.

3. $$\left|\int\limits_{X} f(x) d \mu\right| \leq \sup\limits_{X}|f(x)| \mu(X)$$ (если $$f(x)$$ не ограничена, то правая часть бесконечна).

4. Если $$|f(x)| \leq g(x)$$ и $$g(x)$$ интегрируема, то $$f(x)$$ интегрируема, причем
\

Доказательство: Пусть $$f(x)=\sum\limits_{k=1}^{\infty} f_{k} \chi_{A_{k}}(x), g(x)=\sum\limits_{i=1}^{\infty} g_{i} \chi_{B_{i}}(x)$$, тогда

\
Таким образом получаем, утверждение теоремы. $$\blacksquare$$

Утверждение 1. Пусть $$\left\{f_{n}(x)\right\}$$ — последовательность простых функций со счетным числом значений, $$f_{n}(x)$$ равномерно сходится на $$X$$, тогда числовая последовательность $$\int\limits_{X} f_{n}(x) d \mu$$ равномерно сходится.

Вытекает из оценки

\

Определение 5. Функция $$f(x), x \in X$$, называется интегрируемой по Лебегу на множестве $$X$$, если существует последовательность интегрируемых простых функций со счетным числом значений $$\left\{f_{n}(x)\right\}$$, равномерно сходящаяся к $$f(x)$$ на множестве $$X$$, при этом интегралом Лебега от функции $$f(x)$$ называется

\

Корректность этого определения вытекает из следующего простого утверждения.

Утверждение 2. Если $$\left\{f_{n}(x)\right\}$$ и $$\left\{\tilde{f}_{n}(x)\right\}$$ — две последовательности интегрируемых простых функций со счетным числом значений, равномерно сходящиеся к функции $$f(x)$$ на множестве $$X$$, то

\

Для доказательства достаточно заметить, что

\

Утверждение 3. Пусть функция $$f(x)$$ интегрируема на множестве $$X$$ и пусть последовательность измеримых простых функций со счетным числом значений $$\left\{f_{n}(x)\right\}$$ равномерно сходится к функции $$f(x)$$ на множестве $$X$$, тогда, начиная с некоторого номера, все функции $$f_{n}(x)$$ интегрируемы на множестве $$X$$.

Доказательство: Так как функция $$f(x)$$ интегрируема, то существует последовательность интегрируемых простых функций со счетным числом значений $$\left\{\tilde{f}_{n}(x)\right\}$$, которая равномерно сходится к функции $$f(x)$$. Следовательно, $$\forall \varepsilon>0 \quad \exists N: \forall n \geq N$$
$$\left|\tilde{f}_{n}(x)-f(x)\right|<\varepsilon$$ и (в силу равномерной сходимости) $$\left|f_{n}(x)-f(x)\right|<\varepsilon$$. Отсюда вытекает, что $$\left|\tilde{f}_{n}(x)-f_{n}(x)\right|<2 \varepsilon$$ и $$\left|f_{n}(x)\right|<\left|\tilde{f}_{n}(x)\right|+2 \varepsilon$$, а это и означает интегрируемость $$f_{n}(x)$$. $$\blacksquare$$

Определение 6. Пусть $$f(x)$$ интегрируема на $$X$$, измеримое $$A \subset X$$, тогда по определению

\

где $$\chi_{A}(x)$$ — индикатор-функция множества $$A$$.

Знак интеграла — Википедия (с комментариями)

Ты – не раб! Закрытый образовательный курс для детей элиты: “Истинное обустройство мира”. http://noslave.org

Материал из Википедии — свободной энциклопедии

Символы со сходным начертанием:S · Ѕ · ʃ · Տ · Ⴝ · ട

∫

Знак интеграла (∫) используется для обозначения интеграла в математике. Впервые он был использован немецким математиком и одним из основателей дифференциального и интегрального исчислений Лейбницем в конце XVII века.

Символ «∫» образовался из буквы ſ («длинная s»; от лат. ſumma (summa) — сумма).

Традиции начертания

Русскоязычная традиция начертания знака интеграла отличается от принятой в некоторых западных странах.

• American integral.gif

  В англоязычной традиции, реализованной в системе LaTeX, символ существенно наклонён вправо.

• German integral.gif

  Немецкая форма интеграла вертикальна.

• Russian integral.gif

  В русскоязычной литературе символ выглядит так.

Примечания

1. ↑ Florian Cajori. A history of mathematical notations. — Courier Dover Publications, 1993. — P. 203. — 818 p. — (Dover books on mathematics). — ISBN 9780486677668.

Литература

Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — СПб: ЛКИ, 2007. — 248 с.

Ссылки

•  (нем.)
• [gallica.bnf.fr/scripts/catalog.php?Mod=i&Titre=&FondsTout=on&FondsTxt=on&FondsImp=on&FondsPer=on&FondsImg=on&FondsAud=on&FondsMan=on&Auteur=Leibniz&Sujet=&RPT= Полное собрание трудов (PDF)]
• www.fileformat.info/info/unicode/char/222b/index.htm

Отрывок, характеризующий Знак интеграла

15 го числа утром, на третий день после этого, у Слободского дворца стояло бесчисленное количество экипажей.
Залы были полны. В первой были дворяне в мундирах, во второй купцы с медалями, в бородах и синих кафтанах. По зале Дворянского собрания шел гул и движение. У одного большого стола, под портретом государя, сидели на стульях с высокими спинками важнейшие вельможи; но большинство дворян ходило по зале.

Метод прямоугольников

Наиболее очевидным способом численного интегрирования является прямое вычисление суммы Римана: промежуток, на котором берется интеграл, разбивается на nnn промежутков меньшего размера, и в середине каждого такого промежутка вычисляется значение подинтегральной функции. Сумма таких значений, домноженных на длину промежутка, аппроксимирует значение интеграла. Математически это записывается как

∫abf(x)dx≈∑i=1nf(xi−xi−12)(xi−xi−1).\int\limits_a^b f(x) \, dx \approx \sum\limits_{i=1}^n f(\frac{x_i-x_{i-1}}{2}) (x_i-x_{i-1}) .a∫b​f(x)dx≈i=1∑n​f(2xi​−xi−1​​)(xi​−xi−1​).

Выражение под знаком суммы является площадью прямоугольника. Размер каждого промежутка может быть разным.

Применение интеграла с кружочком в физике

Интеграл с кружочком – это математический символ, который часто применяется в физике для описания различных физических величин. Он представляет собой математическую операцию интегрирования, которая позволяет найти площадь под кривой на графике функции.

В физике интеграл с кружочком может быть использован, например, для нахождения площади под кривой графика зависимости скорости от времени. В этом случае, если скорость тела меняется во времени, можно построить график функции скорости от времени и найти площадь под этой кривой. Интеграл с кружочком позволяет найти точное значение этой площади.

Еще одним примером применения интеграла с кружочком в физике может служить нахождение работы силы, приложенной к телу. Работа силы определена как скалярное произведение вектора силы на перемещение тела. Если сила не является постоянной, то полезно использовать интеграл с кружочком для определения работы, так как это позволяет учесть изменение силы во всем пути.

Кроме того, интеграл с кружочком применяют для нахождения энергии системы. В физике существует закон сохранения энергии, который говорит о том, что энергия системы остается постоянной, если на нее не действуют внешние силы. Интеграл с кружочком позволяет вычислить полную энергию системы, учитывая вклад от всех ее частей.

Таким образом, интеграл с кружочком является мощным математическим инструментом, который находит широкое применение в физике. Он позволяет решать различные задачи, связанные с определением площадей, работы силы и энергии системы. Понимание и использование этого понятия является необходимым для успешного изучения физики и решения физических задач.

Аппроксимация и точность результата

Аппроксимация – принцип, заключающийся в использовании некоторых приближений для оценки значения интеграла с кружочком. В контексте интеграла с кружочком, аппроксимация позволяет приближенно вычислить площадь под кривой путем разбиения ее на небольшие участки и приближенного подсчета площади каждого участка. Чем меньше участков, тем более точным будет приближение.

Точность результата – это степень приближенности результата при вычислении интеграла с кружочком. Чем более точное приближение используется и чем меньше ошибки при аппроксимации, тем более точным будет результат вычисления. Ошибки при аппроксимации могут возникать вследствие недостаточного количества участков, неправильного выбора метода аппроксимации или других факторов.

Для улучшения точности результата можно использовать различные методы аппроксимации, такие как метод прямоугольников, метод трапеций или метод Симпсона. Эти методы основаны на разбиении области под кривой на множество маленьких участков и приближенном подсчете площади каждого участка. Чем больше участков используется при аппроксимации, тем более точным будет результат.

Оценка точности результата может быть выполнена путем сравнения полученного значения интеграла с кружочком с точным значением, если оно известно. Также можно использовать методы аналитической оценки точности, которые основаны на математическом анализе свойств аппроксимации и позволяют оценить погрешность приближения.

Теоремы

Любое разумное понятие интеграла должно удовлетворять свойствам линейности и монотонности . Интеграл Лебега не исключение: если f и g — интегрируемые функции, а a и b — действительные числа, то af + bg интегрируем и  ; если f ≤ g , то (и таким же образом, заменяя два ≤ на <, если область интегрирования имеет ненулевую меру), в частности . Докажем, что это неравенство верно и для f с комплексными значениями.
∫(вж+бграмм)dμзнак равнов∫жdμ+б∫граммdμ{\ displaystyle \ int (af + bg) \, \ mathrm {d} \ mu = a \ int f \, \ mathrm {d} \ mu + b \ int g \, \ mathrm {d} \ mu}∫жdμ≤∫граммdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu \ leq \ int g \, \ mathrm {d} \ mu}|∫жdμ|≤∫|ж|dμ{\ Displaystyle \ влево | \ int е \, \ mathrm {d} \ mu \ right | \ leq \ int | f | \, \ mathrm {d} \ mu}

Две функции, которые различаются только на нулевом множестве измерений μ (тогда мы говорим, что f и g равны μ-почти всюду), имеют один и тот же интеграл, или, точнее: если , то f интегрируема тогда и только тогда, когда g интегрируема, и в этом случае .
μ({Икс∈Икс,ж(Икс)≠грамм(Икс)})знак равно{\ Displaystyle \ му (\ {х \ в Икс, е (х) \ neq г (х) \}) = 0}∫жdμзнак равно∫граммdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu = \ int g \, \ mathrm {d} \ mu}

Любая интегрируемая функция со значениями в ℝ конечна почти всюду, то есть сказать , что множество точек , где она принимает значения ± ∞ имеет нулевую меру.

По сравнению с интегралом Римана одним из существенных преимуществ интеграла Лебега является легкость, с которой происходит предельный переход. Следующие три теоремы являются одними из наиболее часто используемых:

• Теорема о монотонной сходимости  : если — возрастающая последовательность положительно измеримых функций ( т.е.для всех k , f _k ≤ f _{k + 1} ) и если f = lim f _k , то f измерима и последовательность общего члена сходится к (примечание: здесь может быть бесконечно);(жk){\ Displaystyle (е_ {к})}∫жkdμ{\ Displaystyle \ int е_ {к} \, \ mathrm {d} \ mu}∫жdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu}∫жdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu}
• Лемма Фату  : если — последовательность положительно измеримых функций и если f = lim inf f _k , то (опять же, может быть бесконечным);(жk){\ Displaystyle (е_ {к})} ∫жdμ≤lim inf∫жkdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu \ leq \ liminf \ int f_ {k} \, \ mathrm {d} \ mu}∫жdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu}
• Сходимость, основанная на теореме  : если — последовательность измеримых функций, точно сходящихся почти всюду к функции f , и если существует интегрируемая функция g такая, что для всех k , то f интегрируема и следующий общий член сходится .(жk){\ Displaystyle (е_ {к})}|жk|≤грамм{\ displaystyle | f_ {k} | \ leq g}∫жkdμ{\ Displaystyle \ int е_ {к} \, \ mathrm {d} \ mu}∫жdμ{\ Displaystyle \ int е \, \ mathrm {d} \ mu}