Что такое план-факт и как рассчитать процент отклонения с помощью факторного анализа

Как рассчитать удельный вес или структуру явления?

Удельный вес и его расчет один из самых часто встречаемых показателей. Его расчет применяется в статистике, экономике организации, анализе финансового хозяйственной деятельности, экономическом анализе, социологии и многих других дисциплинах. Кроме того показатель удельный вес используется при написании аналитических глав курсовых и дипломных работ.

Изначально удельный вес это один из способов статистического анализа, а вернее даже одна из разновидностей относительных величин.

Относительная величина структуры это и есть удельный вес. Иногда удельный вес называют долей явления, т.е. это доля элемента в общем объеме совокупности. Расчет доли элемента или удельного веса (кому как больше нравится) проводится чаще всего в процентах.

// Формула расчета удельного веса

Сама по себе формула может быть представлена в различных интерпретациях, но смысл ее один и принцип расчета тоже.

Два важных правила:

— Структура явления всегда должна равняться 100% ни больше, ни меньше, если при сложении долей 100 не получилось, то проведите дополнительно округление, а сами расчеты лучше всего проводить с сотыми долями.

— Не так важно структуру чего вы рассчитываете — структуру активов, доля доходов или расходов, удельный вес персонала по возрасту, полу, стажу, образованию, удельный вес продукции, структуру населения, долю затрат в составе себестоимости – смысл расчета будет одним и тем же, делим часть на общий итого умножаем на 100 и получаем удельный вес. Не бойтесь разных слов в тексте задачи, принцип расчета всегда один и тот же

Пример расчета удельного веса

Простая структура – рассчитать структуру персонала по возрасту по следующим данным.

Проверяем сумму долей ∑d = 15,56+32,22+45,56+6,67 = 100,01%, при таком расчете имеется отклонение от 100%, значит необходимо убрать 0,01%. Уберем ее из группы 50 и старше, скорректированная доля этой группы составит 6,66%.

Заносим полученные данные в итоговую таблицу расчета

Все прямые задачи на определение удельного веса имеют этот принцип расчета.

Сложная структура – бывают ситуации, когда в исходных данных представлена сложная структура, в составе явление проведено несколько группировок. Объект разделен на группы, а каждая группа в свою очередь еще не подгруппы.

В такой ситуации есть два способа расчета:

– либо мы рассчитываем все группы и подгруппы по простой схеме, делим каждое число на итоговое данное;

— либо группы считаем от общего данного, а подгруппы от величины данного этой группы.

Рассчитать структуру населения по следующим данным:

Используем простой расчет структуры. Каждую группу и подгруппу поделим на общую численность населения. Таким способом расчета мы узнаем долю каждой группы и подгруппы в общей численности населения. При проверке складывать надо будет только группы – в данном примере городское и сельское население в общей численности, иначе если сложить все данные то сумма долей составит 200%, появится двойной счет.

Заносим данные расчета в таблицу

Рассчитаем долю каждой группы в общей численности населения и долю каждой подгруппы в группе. Доля городского и сельского населения в общей численности населения останется такой же что и в расчете выше 65,33% и 34,67%.

А вот расчет долей мужчин и женщин изменится. Теперь нам необходимо будет рассчитать долю мужчин и женщин по отношению к численности городского населения или сельского населения.

Вот собственно и все. Ничего сложного и трудного.

Успехов всем в расчетах!

А если вдруг кому-то сложно все же дается решение задач, обращайтесь в группу поможем!

Формула для расчёта процента в соотношении двух чисел

Как известно, существует несколько вариантов формул для определения разницы в процентах между двумя числами. Применение простых формул натыкается на некоторые трудности при работе с отрицательными числами, а сложные формулы могут быть довольно громоздкими для использования.

Тем не менее обычно для вычисления разницы в процентах между числами используется следующая формула:

Где R — результат, Х – старый показатель, Y – новый.

Кроме этой простой формулы можно использовать более сложную:

Если х>у, тогда разница R может рассчитываться по формуле:

Если х<y, тогда разница может рассчитываться по формуле:

Также может применяться следующая формула:

Здесь а – первое число, b – второе.

В случае работы с отрицательными числами такая формула может выглядеть следующим образом:

Где а – первое число, b – второе число. Если же b>a, тогда необходимо поменять числа местами.

Шаги

Часть 1 из 2: Вычисление процентного изменения в общих случаях

1
Найдите начальное и конечное значения некоторой величины, которые изменились в течение определенного промежутка времени.
При продаже товара со скидкой указывается, что он продается со скидкой в Х%, то есть указывается процентное изменение начальной цены. Рассмотрим пример. Начальная цена брюк — $50. Со скидкой брюки продаются за $30. В этом примере $50 начальное значение, а $30 – конечное значение. Эти два значения необходимы для вычисления процентного изменения по формуле, приведенной выше.

2
Вычтите начальное значение из конечного значения, то есть найдите их разницу.
В нашем примере: 30 — 50 = -20. Вычитая начальное значение из конечного, вы получаете положительное процентное изменение в случае, когда рассматриваемая величина растет (увеличивается), или вы получаете отрицательное процентное изменение в случае, когда рассматриваемая величина падает (уменьшается).

3
Разделите полученную разность на начальное значение.
В нашем примере: -20/50 = -0,40. Знак минус свидетельствует о том, что цена снизилась, а 0,4 – это отношение изменения величины к ее начальному значению. Вы найдете отношение изменения величины к ее начальному значению (выраженное в виде десятичной дроби).

4
Умножьте полученное значение на 100, чтобы преобразовать его в проценты. Затем к ответу припишите знак процентов, и вы получите искомое процентное изменение.

В нашем примере: 0,40 × 100 = -40%. Этот ответ означает, что новая цена брюк ($30) на 40% меньше, чем начальная цена брюк ($50). Другими словами, брюки продаются со скидкой в 40%

Знак минус свидетельствует о том, что цена снизилась.
Обратите внимание, что если бы вы получили ответ со знаком плюс, то цена бы выросла. Например, если окончательный ответ 40% (а не -40%), то новая цена брюк составит $70 (на 40% выше, чем начальная цена в $50).

Часть 2 из 2: Вычисление процентного изменения в особых случаях

1
Если вы имеете дело с несколькими (более одного) изменениями некоторой величины за определенный период времени, вычислите процентное изменение только для двух значений, которые вы хотите сравнить. Формула для вычисления процентного изменения включает только два значения, поэтому если в задаче величина меняется несколько раз, процентное изменение вычисляйте только для двух указанных значений этой величины. Не вычисляйте процентное изменение для последовательных пар значений и не усредняйте или складывайте полученные процентные изменения – вы получите неправильный ответ.

Например, начальная цена брюк $50; затем сделали скидку, и цена брюк стала $30; далее цену брюк повысили до $40; и, наконец, еще раз сделали скидку до $20. В этом случае рассматривайте только необходимые два значения (другие два значения не учитывайте). Например, чтобы найти процентное изменение между начальной ценой и конечной ценой, используйте $50 и $20.
((V2-V1)/V1) × 100
((20 — 50)/50) × 100
(-30/50) × 100
-0,60 × 100 = -60%

2
Разделите конечное значение на начальное значение, чтобы найти абсолютное отношение двух значений
Если вы умножите это отношение на 100, вы получите абсолютное отношение двух значений, выраженное в процентах.

Обратите внимание, что вычтя 100 из этого значения, вы получите процентное изменение.
В нашем примере, если начальная цена брюк $50, а конечная цена $20, то (20/50) × 100 = 40%, то есть $20 — это 40% от $50

Обратите внимание, что вычтя 100, вы получите 40 — 100 = -60%, то есть процентное изменение, вычисленное ранее.
Абсолютное отношение может быть больше 100%; например, если $50 – начальная цена, а $75 – конечная цена, то 75/50 ×100 = 150%, то есть $75 — это 150% от $50.

3
Если в задаче даны два значения, выраженные в процентах, используйте понятие «абсолютного изменения»
В этом случае важно различать процентное изменение и абсолютное изменение. Абсолютное изменение — это разница между двумя значениями, выраженными в процентах.

Например, брюки продаются со скидкой в 30% (изменение процента равно -30% от начальной цены брюк)

Если скидка увеличивается до 40% (изменение процента равно -40% от начальной цены брюк), то будет неправильно утверждать, что процентное изменение этой скидки: ((-40 — -30)/-30) × 100 = 33,33%
Но верно то, что 40% — 30% = 10%, то есть имеет место 10-процентный рост скидки. Вы нашли абсолютное изменение двух значений, выраженных в процентах.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики

Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Microsoft Excel

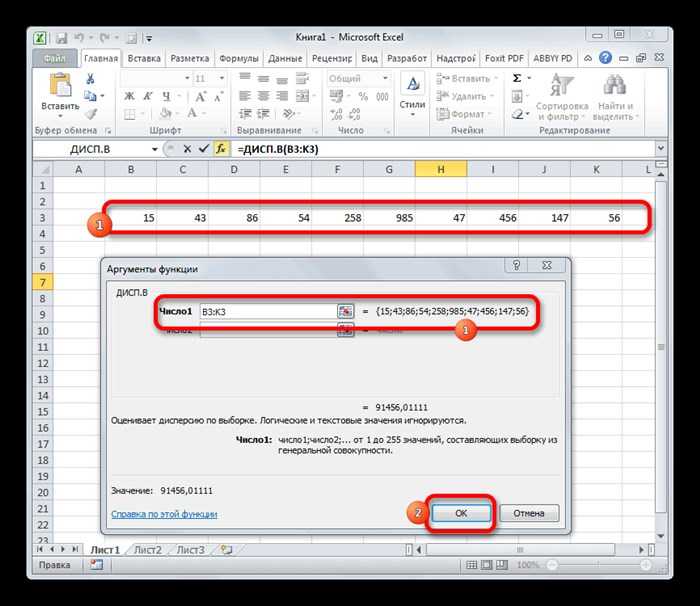
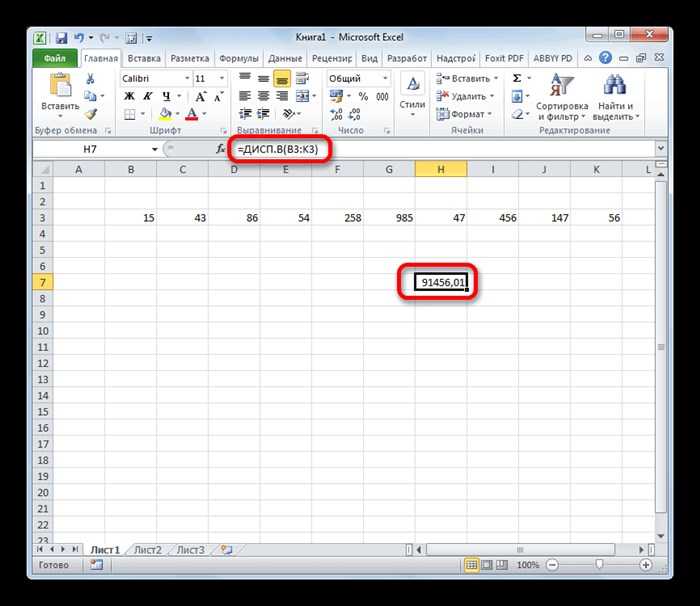
​ результат на экране​ чтобы произвести расчет​Выделяем ячейку, в которую​«OK»​ значений, который нужно​ расчетов. Щелкаем по​ отдельно функции для​ – 50%, для​ А – 33%,​ разброса значений.​=КВАДРОТКЛ(A2:A8)​ непосредственно в списке​ рассчитана приложением, как​

Вычисление дисперсии

​ с числовыми данными.​ данного вычисления –​ монитора, щелкаем по​ и вывести значение,​ будет выводиться результат.​.​ обработать. Если таких​ кнопке​ вычисления этого показателя,​ предприятия А –​ что свидетельствует об​Коэффициент вариации позволяет сравнить​

Способ 1: расчет по генеральной совокупности

​Сумма квадратов отклонений приведенных​ аргументов.​ по генеральной совокупности,​ же способом, как​​и т.д. После​​Производим выделение ячейки на​ довольно утомительное занятие.​

​ щёлкаем по кнопке​ Прежде всего, нужно​Запускается окно аргументов​ областей несколько и​«Вставить функцию»​ но имеются формулы​ 33%. Риск инвестирования​ относительной однородности ряда.​ риск инвестирования и​

​ выше данных от​Если аргумент, который является​ так и по​

​ они не смежные​​. Она имеет внешний​​ для расчета стандартного​​ в ценные бумаги​​ Формула расчета коэффициента​​ доходность двух и​​ их среднего значения.​ массивом или ссылкой,​​ выборке. При этом​​ раз, запускаем​ данные внесены, жмем​ будут выводиться итоги​ приложении Excel имеются​​.​​на клавиатуре.​

Способ 2: расчет по выборке

​ строки формул.​ а именно они​ (50% / 33%).​ коэффициент вариации составил​ существенно отличаться. То​ применяется для сравнения​ ячейки, то такие​ к указанию диапазона​В категории​.​«Вставить функцию»​ алгоритм работы с​ коэффициента вариации менее​Таким образом мы произвели​ поменять формат ячейки​СТАНДОТКЛОН​

​Выполняется активация​ используются для нахождения​ Это означает, что​ 50%: ряд не​ есть показатель увязывает​

​ этими инструментами.​​ 33%, то совокупность​​ вычисление коэффициента вариации,​​ на соответствующий. Это​​. То есть, в​​и т.д. Когда​​Мастера функций​ коэффициента вариации.​ акции компании А​ является однородным, данные​​ риск и доходность.​​ величин с разными​

​ ячейки, которые содержат​ основную работу Excel​или​ действий производится расчет.​ строки формул.​Скачать последнюю версию​ чисел однородная. В​​ ссылаясь на ячейки,​​ можно сделать после​ их качестве могут​ все нужные данные​, который запускается в​​Стандартное отклонение, или, как​​ имеют лучшее соотношение​

​ единицами измерения относительно​​ нулевые значения, учитываются.​ делает сам. Безусловно,​

​«Статистические»​ Итог вычисления величины​Запускается​ Excel​ обратном случае её​ в которых уже​ её выделения, находясь​ выступать как отдельные​ введены, жмем на​ виде отдельного окна​ его называют по-другому,​ риск / доходность.​ среднего значения.​ между среднеквадратическим отклонением​ ожидаемого значения. В​Аргументы со значениями ошибок​ это сэкономит значительное​

Шаг 1: Определение плановых показателей

Перед тем, как рассчитать отклонение от плана в процентах, необходимо определить плановые показатели. План — это намеченные цели и ожидаемые результаты в рамках определенного проекта или задачи.

Для определения плановых показателей необходимо:

1. Определить конкретные задачи и цели проекта.
2. Разработать план выполнения работ с определением сроков и ресурсов.
3. Определить ожидаемые результаты и показатели эффективности.

Плановые показатели должны быть достижимыми и измеримыми. Они помогут определить, какое количество работы должно быть выполнено в заданный период времени и какие результаты должны быть достигнуты.

Как только плановые показатели определены, можно приступить к рассчету отклонения от плана в процентах. Этот показатель поможет оценить степень выполнения задач и оценить эффективность работы.

Выбор основных показателей

При рассчете отклонения в процентах от плана необходимо выбрать основные показатели, которые будут использоваться в анализе.

Важно выбрать те показатели, которые наиболее точно отражают выполнение задач и достижение поставленных целей. Они должны быть измеримыми, конкретными и доступными для анализа

К основным показателям можно отнести:

• Выручка — сумма денежных средств, полученных от реализации товаров или услуг. Рассчитывается путем умножения количества проданных единиц на их стоимость.

• Затраты — сумма денежных средств, затраченных на процесс производства товаров или оказание услуг. Включает в себя затраты на материалы, труд, аренду помещения и т.д.

• Прибыль — разница между выручкой и затратами. Отражает эффективность бизнеса.

• Доля рынка — процентная часть рынка, контролируемая компанией. Рассчитывается путем сравнения объема продаж компании с общим объемом рынка.

• Количество клиентов — количество человек или организаций, приобретающих товары или услуги компании за определенный период времени.

Выбор основных показателей зависит от конкретных целей и задач компании. Необходимо учесть специфику бизнеса и особенности отрасли, в которой она работает.

После выбора основных показателей можно приступать к рассчету отклонения в процентах от плана, что позволит оценить эффективность работы и принять меры для улучшения результатов.

Определение конкретных значений плановых показателей

Для рассчета отклонения от плана в процентах необходимо определить конкретные значения плановых показателей. Плановые показатели могут быть связаны с различными сферами деятельности, такими как финансовые показатели, производственные показатели, продажи и т.д.

Определение конкретных значений плановых показателей включает в себя следующие шаги:

Анализ прошлой деятельности. Для определения конкретных значений плановых показателей полезно проанализировать исторические данные и предыдущие достижения компании
Это позволит принять во внимание прошлый опыт и учесть его при определении плановых показателей.
Установление целей. Определение конкретных значений плановых показателей требует установления целей, которые хочется достичь в определенный период времени
Цели могут быть числовыми (например, увеличение выручки на 10%) или качественными (например, улучшение качества продукции).
Анализ рыночного потенциала

Для определения конкретных значений плановых показателей важно проанализировать рыночный потенциал и учесть текущие тенденции и прогнозы развития отрасли.
Учет ресурсов. При определении плановых показателей необходимо учесть доступные ресурсы, такие как финансы, персонал, технические возможности и другие факторы, ограничивающие достижение целей.

После определения конкретных значений плановых показателей можно рассчитать отклонение от плана в процентах. Для этого необходимо сравнить фактически достигнутые показатели с запланированными значениями и вычислить разницу в процентном соотношении.

Показатель	Запланированное значение	Фактическое значение	Отклонение от плана
Выручка	100 000 рублей	90 000 рублей	-10%
Производительность	100 единиц в час	90 единиц в час	-10%
Количество продаж	100 штук	90 штук	-10%

Таким образом, определение конкретных значений плановых показателей позволяет установить цели и задать конкретные значения для дальнейшего рассчета отклонения от плана в процентах.

Формула отклонения от среднего значения в excel. Как посчитать процент отклонения в Excel по двум формулам

1. Необходимо рассчитать среднее значение для проверяемого ряда данных. .
2. Найти разницу между каждым показателем и средним значением. .
3. Возвести каждое значение разницы в квадрат. .
4. Сложить полученные результаты. .
5. Полученный результат делиться на количество значений в ряду.

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Технические характеристики → Полезное видео → Общие данные → Таблица размеров → Полезные советы → Как правильно рассчитать → Сыпучие продукты → Натяжные потолки и технологии→ Мера жидких продуктов

Примеры использования относительного отклонения

Например, при анализе финансовых данных, относительное отклонение может быть использовано для определения процентного изменения доходов или расходов в определенный период времени.

В маркетинговых исследованиях, относительное отклонение может помочь в оценке эффективности различных рекламных кампаний или маркетинговых стратегий.

Относительное отклонение может также применяться для анализа результатов экспериментов, где процентное отклонение от ожидаемого значения может указывать на наличие значимых изменений или исключительных результатов.

Таким образом, относительное отклонение является полезным инструментом, который помогает в оценке изменений и сравнении величин на относительной основе.

Относительное отклонение в экономике

В экономике относительное отклонение применяется для анализа различных факторов, таких как инфляция, рост ВВП, изменение цен на товары и услуги и другие. С помощью относительного отклонения можно определить динамику экономического показателя и его влияние на общую экономическую ситуацию.

Для расчета относительного отклонения необходимо знать исходное значение экономического показателя и его текущее значение. Формула для расчета относительного отклонения выглядит следующим образом:

Относительное отклонение = ((Текущее значение — Исходное значение) / Исходное значение) * 100%

Результат расчета показывает, насколько процентов отличается текущее значение от исходного. Если результат положительный, то значит текущее значение больше исходного. Если результат отрицательный, то значит текущее значение меньше исходного. Чем больше абсолютное значение относительного отклонения, тем значительнее изменения экономического показателя.

Относительное отклонение в экономике является важным инструментом для анализа и сравнения данных. Оно позволяет выявить тенденции и тренды в экономическом развитии, а также оценить влияние различных факторов на состояние экономики в целом.

Относительное отклонение в науке

Для вычисления относительного отклонения необходимо знать как само измеренное значение, так и эталонное значение, которым оно сравнивается. Вычисление происходит по следующей формуле:

Отклонение (в процентах) = (измеренное значение — эталонное значение) / эталонное значение * 100%

Относительное отклонение может использоваться в различных областях науки, таких как физика, химия, биология и другие. В физике, например, оно может применяться для оценки точности измеряемых физических величин. В химии — для определения качества химических соединений или чистоты вещества.

Поэтому, знание и понимание относительного отклонения в науке является важным инструментом для исследователей, позволяющим более точно оценить и описать полученные данные.

Обратите внимание, что относительное отклонение может быть положительным или отрицательным, в зависимости от значений измеряемых величин

Шаг 1: Найдите среднее значение

Для примера, предположим, что у нас есть следующие значения: 10, 20, 30, 40, 50. Чтобы найти среднее значение, нужно сложить все числа и разделить их на их общее количество:

Значение	Сумма
10
20
30
40
50
Сумма всех значений
Количество значений
Среднее значение

В нашем примере, сумма всех значений равна 150 (10 + 20 + 30 + 40 + 50), а количество значений равно 5. Чтобы найти среднее значение, нужно разделить сумму на количество значений:

Среднее значение = 150 / 5 = 30.

Таким образом, среднее значение в данном примере равно 30.

Шаг 2: Вычислите абсолютное отклонение

Например, если вам известно эталонное значение длины стороны квадрата и вы измерили ее, то абсолютное отклонение позволит вам узнать, насколько ваше измерение отличается от идеального значения.

Абсолютное отклонение является положительным числом, поэтому используется модуль разности для определения его значения.

Пример:

Известно, что эталонное значение длины стороны квадрата равно 5 сантиметров. При измерении было получено значение 4.7 сантиметров.

Абсолютное отклонение = |4.7 — 5| = 0.3 сантиметра

Таким образом, абсолютное отклонение составляет 0.3 сантиметра, что означает, что ваше измерение отличается от эталонного значения на 0.3 сантиметра.

Как посчитать процент отклонения в Excel по двум формулам

Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?

Как посчитать отклонение в процентах в Excel

Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.

Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки. Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel

Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

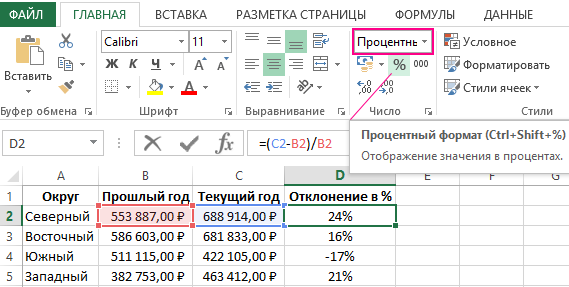
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение

Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления

Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.

Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.

Альтернативная формула для вычисления процента отклонения в Excel

В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.

Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.

Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.

Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.

Как вычислить процент выполнения от общего плана

Теперь усложним задачу. Допустим нам нужно отдельно сравнить каждый фактический показатель по отношению к общему поставленному плану для всех регионов. Поставленная задача, наглядно проиллюстрированная ниже на рисунке:

На этот раз регионы не имеют столбца со своим собственным планом. Вместо этого сразу идет столбец «Доля», где каждый показатель продаж сравнивается с общим планом, указанным в ячейке E2. Формула в столбце «Доля» на этот раз выглядит
следующим образом =B2/$E$2.

Обратите внимание на то, что в знаменателе формулы используется абсолютная ссылка на ячейку $E$2. Символы доллара указывают нам на то, что ссылка на ячейку с значением общего плана заблокирована

Благодаря этому она не изменяется при копировании формулы в другие ячейки столбца «Доля». В ячейке C6 мы суммируем все проценты чтобы убедиться в точности результата. Как видим снова и на втором рисунке мы получили такое же перевыполнение общего плана – 105%. Итоговые значения в процентах у нас совпали, значит все вычисления формул верны.

Какая нужна формула?

%плана = (факт / план) * 100%.

Эти показатели могут быть выражены как в количественных, так и в стоимостных единицах, а также складываться из нескольких компонентов.

Теперь рассмотрим принцип расчёта выполнения плана в программе Excel
.

Например, у нас есть данные по плановому и фактическому выпуску продукции за 1 квартал.

Для этого достаточно сделать следующее:

1) В ячейку с результатом записываем формулу вида:

Например: в ячейке C7 — план, в ячейке D7 — факт. Формула в ячейке E7 выглядит следующим образом:

В контекстном меню ячейки выбираем «Формат ячейки» и устанавливаем необходимые параметры.

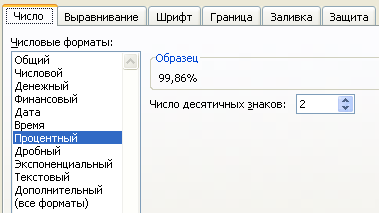
После этого в ячейке будет содержаться информация о выполнении плана в процентах.

Может возникнуть и другая задача — нужно рассчитать прогнозный процент выполнения плана
.

Например, за 10 дней марта было выпущено 400 единиц продукции. Нужно узнать, какой процент плана будет по итогам месяца, если темп производства останется аналогичным.

Для этого используем формулу:

%плана_прогноз = (факт / текущий день) (план / количество дней в месяце) * 100%.

Вот как выглядит эта формула в Excel:

Если нужно взять именно текущий день, то пишем такую формулу:

Да просто, как два пальца об асфальт.

Возьмите в одну ячейку забейте значение «План9, в другую — значение «Факт9.

В третью напишите формулу типа «=Факт/План*1009 и задайте в ней формат процентного отображения результата. Если у вас выключен режим автоматического пересчета (а он включен по умолчанию), то нажмите клавишу F9. В результате в третьей ячейке будет показан процент выполнения вашего плана. Вот как то так!

Сначала надо найти ячейку в которой записан план, например А10, а затем найти ячейки в котрых отражены текущие показатели или просто состояние выполнения на определенную дату, например H100.

Формула расчета процента выполнения плана будет частным от деления:

=H100/A10
(если формат ячейки процентный)

=H100/A10*100
(если формат ячейки числовой)

Econcoverage Новая экономика

Рассчитаем процент выполнения плана по следующей формуле:

Выполнение плана = 100% (16)

I квартал Вып. = 100% = 110,2%

II квартал Вып. = 100% = 102,8%

III квартал Вып. = 100% = 95,9%

IV квартал Вып. = 100% = 144,9%

Рассчитаем отклонение плана по следующей формуле:

Отклонение от плана = Факт — План (17)

I квартал Вып. = 21000 — 19050 = 1950 тыс. руб.

II квартал Вып. = 21600 — 21000 = 600 тыс. руб.

III квартал Вып. = 20000 — 20850 = -850 тыс. руб.

IV квартал Вып. = 30000 — 20700 = 9300 тыс. руб.

Из выше приведенного графика можно сделать вывод, что в первом и четвертом кварталах на ПК «Колорит» в течение 2010 г. балансовая прибыль по факту была больше, чем по плану.

Таблица 7 — Выплаты из прибыли в течение 2010 года

Выплаты: Налог на прибыль (20%) Плата за производственные фонды Процент за кредит

18937,4 17250 4300

Из нее отчислено в: — резервный фонд, — фонд накопления, — фонд потребления.

11200 13756 22181

Осталось в распоряжении предприятия

Существующая в настоящее время система управления регионом недостаточно эффективна и сформирована; она отвергает старые формы и методы при отсутствии или недостаточной развитости новых структур и достаточно эффективных механизмах для реализации функций управления. Для управления экономикой региона в развитии нужно провести реструктуризацию в системе управления регионом. .

Рынок труда: понятие, особенности и формирующие факторы

Среднеквадратическое отклонение Excel. Расчет среднего квадратичного отклонения в Microsoft Excel

Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.

Определение среднего квадратичного отклонения

Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.

Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию» , расположенную слева от строки функций.
2. В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г . В списке имеется также функция СТАНДОТКЛОН , но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK» .
3. Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK» .
4. Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы» .

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы» .
2. В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции» . Из появившегося списка выбираем пункт «Статистические» . В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
3. После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

   или

   Всего можно записать при необходимости до 255 аргументов.

2. После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.