Что означает координатная четверть?

Четыре квадранта координатной плоскости: важность и примеры использования

Четыре квадранта на координатной плоскости нумеруются по часовой стрелке, начиная с верхнего правого квадранта:

1. Первый квадрант (I) находится в верхней правой части плоскости. Он содержит точки с положительными значениями по обоим осям.
2. Второй квадрант (II) находится в верхней левой части плоскости. Он содержит точки с отрицательными значениями по оси X и положительными значениями по оси Y.
3. Третий квадрант (III) находится в нижней левой части плоскости. Он содержит точки с отрицательными значениями по обоим осям.
4. Четвертый квадрант (IV) находится в нижней правой части плоскости. Он содержит точки с положительными значениями по оси X и отрицательными значениями по оси Y.

Четыре квадранта координатной плоскости играют важную роль в различных областях, таких как физика, математика, инженерия и программирование. Они помогают определить расположение точек на плоскости и вычислить различные параметры.

Примеры использования четырех квадрантов координатной плоскости включают:

1. Анализ движения тела: в физике с помощью четырех квадрантов определяют положение и направление движения объектов.
2. Построение графиков функций: в математике график функции можно разместить на координатной плоскости, используя четыре квадранта.
3. Навигация и картография: в навигации и картографии координатная плоскость с квадрантами используется для определения местоположения и пути движения.
4. Работа с графическими программами: в программировании четыре квадранта координатной плоскости используются для создания и манипулирования графическими объектами.

Таким образом, четыре квадранта координатной плоскости играют важную роль в понимании и использовании системы координат, а также расширяют возможности в различных областях науки и техники.

Координаты точки в декартовой системе координат

Для начала поставьте точку М на оси быка. Любое действительное число xM равно единственной точке M, лежащей на этой прямой. В этом случае начало координатных линий всегда равно нулю.

Каждая точка M, которая находится на Ox, равна действительному числу xM. Это действительное число равно нулю, если точка M находится в начале координат, то есть на пересечении Ox и Oy. Если точка удаляется в положительном направлении, длина сегмента положительна, и наоборот.

Число xM — это координата точки M на данной координатной прямой.

Пусть точка является проекцией точки Mx в Ox и My в Oy. Это означает, что через точку M можно провести прямые, перпендикулярные осям Ox и Oy, после чего мы получим соответствующие точки пересечения Mx и My. Тогда точке Mx на оси Ox соответствует номер xM, а My на Oy — yM. Как это отображается на осях координат:

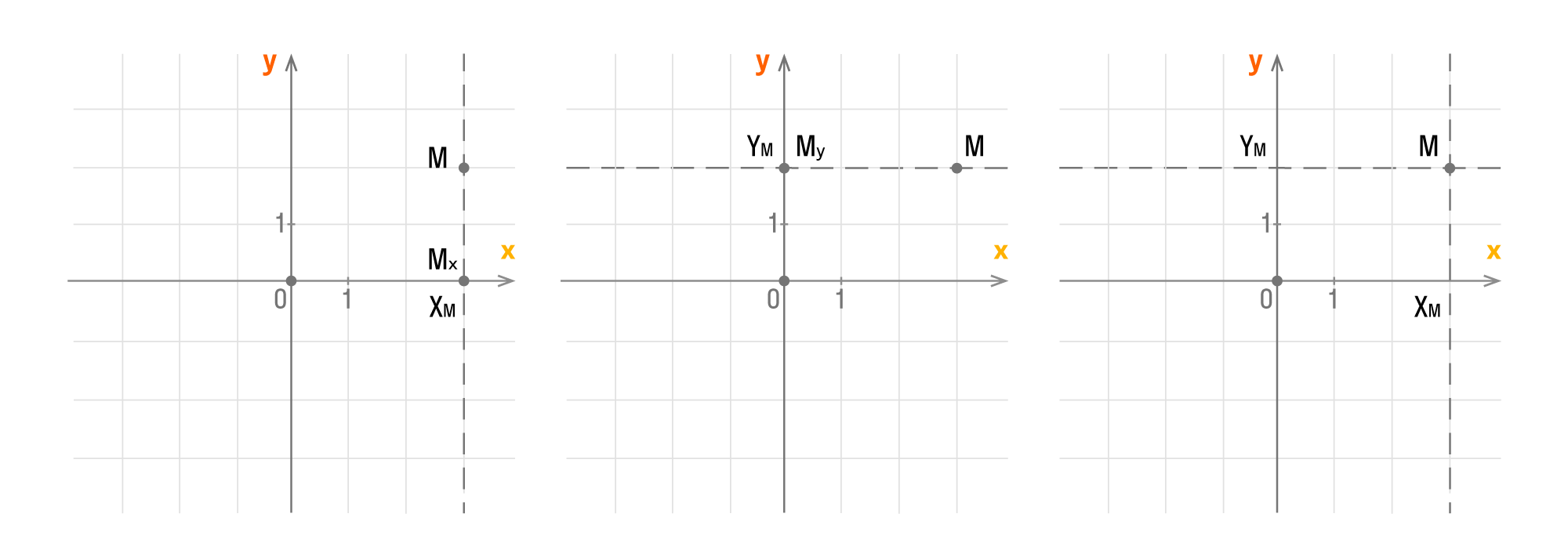
Каждой точке M на данной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса M — xM, ордината M — yM.

верно и обратное: каждой паре (xM, yM) соответствует точка на плоскости.

Примеры использования координатной четверти

Координатная четверть широко применяется в различных областях науки и техники. Ниже приведены некоторые примеры использования координатной четверти:

• Математика: В математике координатная четверть используется для определения положения точки в двумерном пространстве. Координаты точки вида (x, y) указывают ее расположение относительно начала координат. Два числа x и y могут быть положительными, отрицательными или равными нулю, что позволяет определить точку в одной из четырех координатных четвертей.
• Физика: Координатная четверть применяется в физике для анализа движения тела. Например, при моделировании движения объекта, можно использовать координатные четверти для отслеживания его положения и скорости в разных направлениях.
• Графики и дизайн: В графическом дизайне и компьютерной графике координатная четверть используется для размещения и редактирования элементов на двумерной плоскости. Относительные координаты x и y позволяют точно указать местоположение объектов в рамках выбранной координатной системы.
• География: В географии координатная четверть используется для определения широты и долготы точек на глобусе или карте. Широта указывает на расстояние от точки до экватора (северная или южная полушария), а долгота определяет расположение точки по отношению к меридиану Гринвича (восточная или западная полушария).
• Навигация: В навигации координатная четверть используется для определения местоположения объектов и навигационных точек. GPS-навигаторы и другие системы навигации используют координаты для точного определения положения объектов на Земле.

Это лишь несколько примеров использования координатной четверти. Она широко применяется во многих областях, где требуется точное определение положения объектов или анализ их движения.

Симметрия относительно осей

Представь себе, что у нас есть ось. Например, вертикальная ось. Теперь визуализируй себе точку на этой оси. Теперь представь, что есть точка, симметричная первой точке относительно этой оси. То есть, если первая точка находится выше оси, то вторая точка будет находиться под осью на том же самом расстоянии.

Ну, и если ось горизонтальная, то все то же самое, только точки будут располагаться справа или слева от оси.

Так что, симметрия относительно осей — это просто находить точку, которая находится на том же самом расстоянии от оси, что и первоначальная точка, но расположенная на другой стороне.

О задаче сопряжения для гиперболического и псевдопараболического уравнений четвертого порядка

Актуальность работы обусловлена доказательством корректности задачи сопряжения для линейного гиперболического и псевдопараболического уравнений четвертого порядка с младшими членами. Цель работы: доказательство существования и единственности решения задачи сопряжения для гиперболического и псевдопараболического уравнений четвертого порядка, когда условия сопряжения задаются на не характеристической линии Методы исследования: Методом функции Римана и интегральных уравнений разрешимость задачи эквивалентным образом сводится к решению системы интегральных уравнений Фредгольма второго рода, решение которого устанавливается методом последовательных приближений. Результаты: В работе исследована разрешимость задачи сопряжения для гиперболического и псевдопараболического уравнений четвертого порядка с младшими переменными коэффициентами. Установлено, что когда порядок уравнения равен четырем и условия сопряжения задаются на не характеристической линии, то для корректности задачи, вместо обы…

Векторный способ задания положения точки .

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор

М

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор

t
векторным законом (векторным уравнением) движения точкиМ

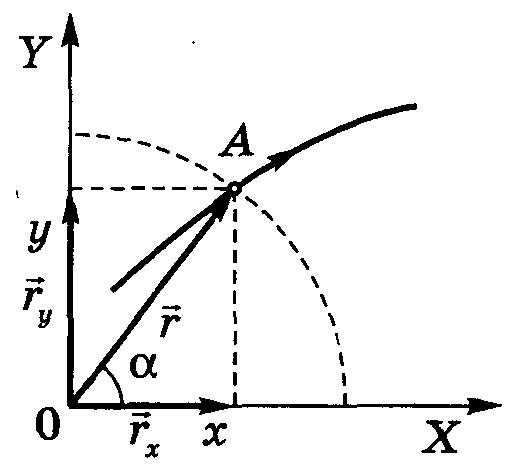
Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за

r_xr_yxyА

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

Источник

Историческая справка

Сегодня каждый школьник, учащийся в шестом классе, не только слышал про координатную плоскость, но и знает правило построения простейших фигур в двумерном пространстве. Но так было не всегда.

Необходимость в определении точного местоположения объектов возникла очень давно. Скорее всего, ещё в древнейшие времена существовали примитивные методы записи координат. Более точные системы возникли в Древней Греции. Их появление было связано с потребностью в картографии.

Достоверно известно, что составитель первой карты Анаксимандр Милетский пользовался географической долготой и широтой, запись которых была основана на прямоугольной проекции. Незадолго до начала нашей эры древнегреческий учёный по имени Гиппарх выдвинул замечательную идею, заключающуюся в опоясывании земного шара параллелями и меридианами и записи информации о положении объектов в виде двух чисел. В Египте на стене одной из усыпальниц археологами был обнаружен рисунок, состоящий из клеточек и представляющий собой координатную сетку.

Автором прямоугольной системы координат на плоскости является математик Рене Декарт, живший во Франции XVII века. История этого гениального открытия весьма забавна. Дело в том, что в театре тех лет ещё не существовало привычной для современной публики нумерации мест. Из-за этого нередко возникала страшная путаница, ссоры, драки и даже дуэли. Будучи талантливым математиком, Декарт предложил новый способ обозначения, базирующийся на двух номерах — ряда и кресла. Это изобретение избавило зрителей от ненужных проблем и произвело настоящий фурор в обществе.

Сегодня при помощи декартовой системы координат можно задать не только расположение простой фигуры, например, треугольника, на плоскости, но и описать любой сложный предмет и его перемещение в пространстве. Метод нашёл широкое применение во многих электронных устройствах и графических программах.

Координатная ось — «фотография» чисел в виде точек на прямой ##

пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.

Чтобы из любой прямой получить координатную ось ,необходимо выбрать на ней нулевую точку$0$- это будет началом отсчета ;отметитьточку$1$ — определить единичный отрезок(т.е. выбрать масштаб)инарисовать стрелочку в положительном направлении отсчёта .На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу$3$на координатной прямойсопоставляется единственная точка$A$, точке$B$-единственное число$-2$, такое число назвали координатой.

Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.

пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.

Координаты точек на прямой.

пробa Точка$O$разбиваетпрямую$AB$на два луча$OA$и$OB$ . Если примем точку$O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось .Рассмотрим на ней произвольную точку .Как определить ее положение?Для ответа на этот вопрос придумали понятие — координата . Положение любой точки на координатной осизадается её координатой.Чтобы отличить друг от друга координаты , перед числами на левом луче$OA$условились ставить знак «минус », а перед числами на правом луче$OB$-знак«плюс».

Координатысо знаком»$-$»называются отрицательными.Координатысо знаком «+» называютсяположительными .

Точка$O$- начало отсчета илиначало координат , изображает ноль.Само число$0$не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .

Координата точки — это число , показывающее положение точки на прямой.

Записывают координаты точек$B$,$C$,$D$следующим образом:$B(-4,2)$,$C\left(-\frac{1}{2}\right)$,$D(3,9)$.

Изображение чисел точками на координатной оси.

Числа на координатной прямой выглядят точками. Для тогочтобыпостроитьточку, соответствующую некоторому числу$a$ , нужно:определить знак этого числа ;от начала координат отложить отрезок , равный$\left|a\right|$вправо , если знак»+»ивлево , еслизнак»-» .

Число$a$в таком случае называют координатой построенной точки .

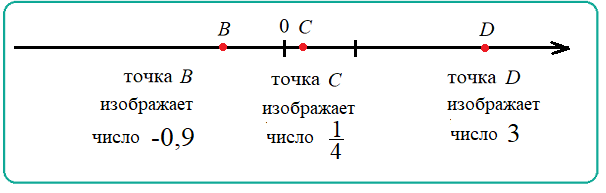
На рисунке числа $3$, $\frac{1}{4}$,$-0,9$изображены соответсвенно точками$B$,$C$,$D$. Числа- это«адреса»точек на координатной прямой.Точки-это»фотографии» чисел.

Введение оси координат:
1) Выбрать на прямой начало координат;
2) Выбрать положительное направление;
3) Выбрать единичный отрезок.

Координаты точки:
Каждой точке можно присвоить свою координату-это расстояние от точки до начала координат с учетом знака: слева от $0$знак $-$ , справа$+$.

Изображение числа : пробa
По любой координате можно восстановить точку.

Шаг 1: нарисуйте график

Первым шагом для определения координатных четвертей расположения графика вам необходимо нарисовать сам график. Для этого вам понадобится координатная плоскость, на которой вы будете отображать значения вашего графика.

Вы можете нарисовать его вручную на бумаге, используя линейку и графические инструменты

Важно следовать принципам создания координатной плоскости: ось абсцисс (горизонтальная ось) должна быть нарисована горизонтально, а ось ординат (вертикальная ось) должна быть нарисована вертикально

Пометьте значения на осях, чтобы отразить масштаб вашего графика. Например, на оси абсцисс вы можете отметить значения от -10 до 10 с шагом 1, а на оси ординат от -10 до 10 с шагом 2.

После того, как вы нарисовали координатную плоскость и отметили значения на осях, приступайте к построению графика. Используйте соответствующие точки или линии, чтобы отобразить значения вашего графика на плоскости.

Если вы предпочитаете использовать графический редактор или программу для рисования графиков, вы можете создать график в цифровом формате. В таком случае у вас будет возможность более точно отобразить значения графика и изменять его в дальнейшем.

Постройте график, и переходите ко второму шагу, чтобы определить координатные четверти расположения графика.

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил использовать математические вычисления вместо геометрических построений. Так появился координатный метод, о котором мы сейчас и поговорим.

Координатами можно назвать номер таблицы в полосе, широту и долготу на географической карте, расположение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем объект набором букв, цифр или других символов, тем самым мы устанавливаем его координаты.

Прямоугольная система координат — это система координат, изобретенная математиком Рене Декартом, также называемая «декартовой системой координат». Представляет собой два взаимно перпендикулярных луча с началом в точке их пересечения.

Чтобы узнать координаты, нужны ориентиры, с которых начнется обратный отсчет. На одном уровне эту роль будут играть две числовые оси.

Рисунок начинается с горизонтальной оси, называемой осью абсцисс, и обозначается латинской буквой x (x). Ось пишется так: Ох. Положительное направление оси абсцисс указано стрелкой слева направо.

Затем проводится вертикальная ось, которая называется осью y и обозначается y (зазор). Ось Oy зарегистрирована. Положительное направление оси ординат показано стрелкой, направленной снизу вверх.

Оси взаимно перпендикулярны, а значит, угол между ними составляет 90 °. Точка пересечения является исходной точкой для каждой из осей и обозначается как: O. Исходная точка делит оси на две части: положительную и отрицательную.

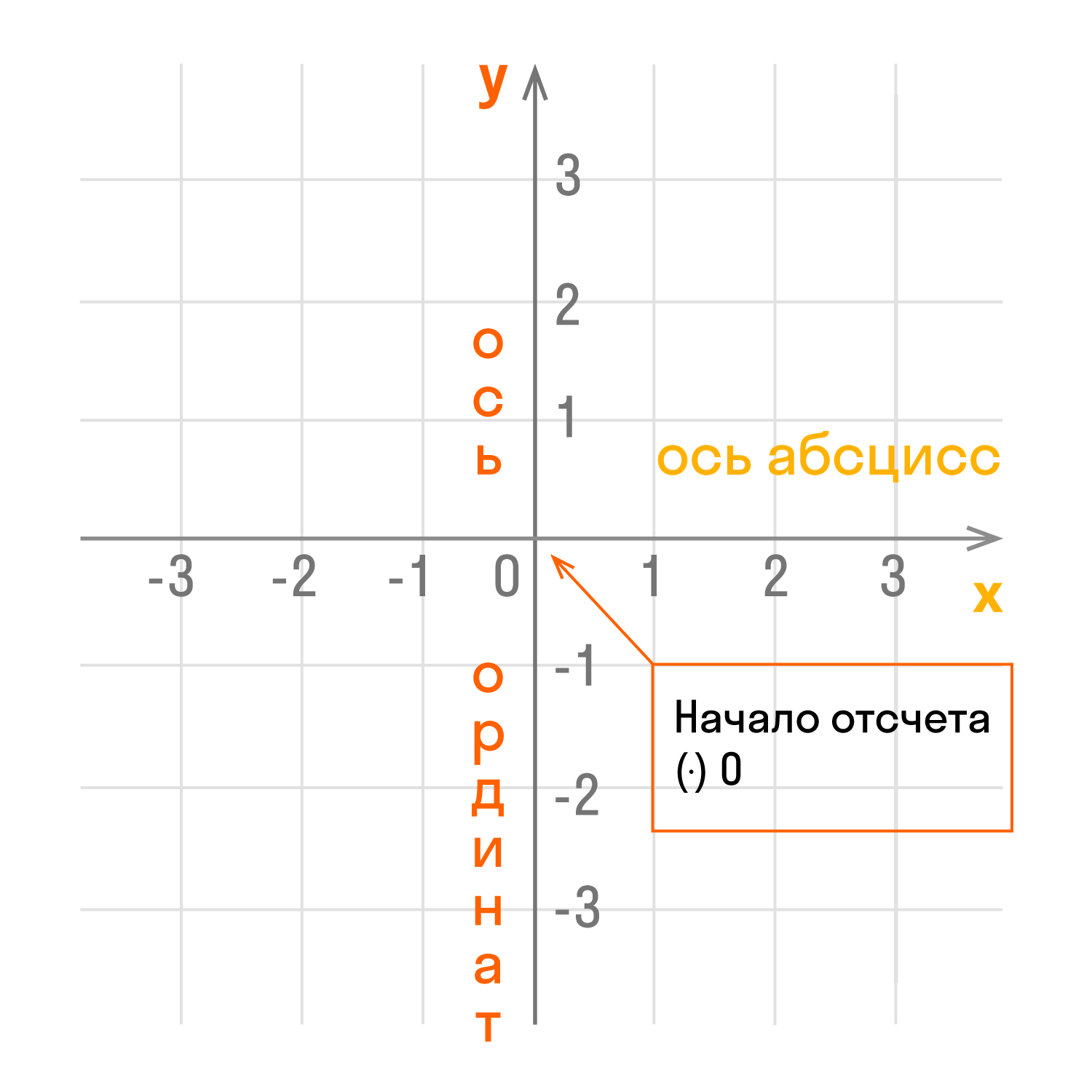
• Оси координат — это прямые линии, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — это вертикальная ось.
• Координатная плоскость — плоскость, в которой расположена система координат. Обозначается это так: x0y.
• Единичный сегмент — это величина, которая принимается за единицу в геометрических конструкциях. В декартовой системе координат на каждой оси нанесена единичная линия. Длина сегмента показывает, сколько раз отдельный сегмент и его части помещаются в данный сегмент.

Единичные линии расположены слева и справа от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy расположены слева или справа, на оси Oy — под ней. Чаще всего единичные сегменты двух осей соответствуют друг другу, но есть задачи, в которых они не равны.

Оси координат делят плоскость на четыре угла — четыре четверти координат.

Каждая из согласованных кварталов имеет свой номер и обозначение в виде римской цифры. Обратный отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• левый верхний угол — вторая четверть II;
• левый нижний угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

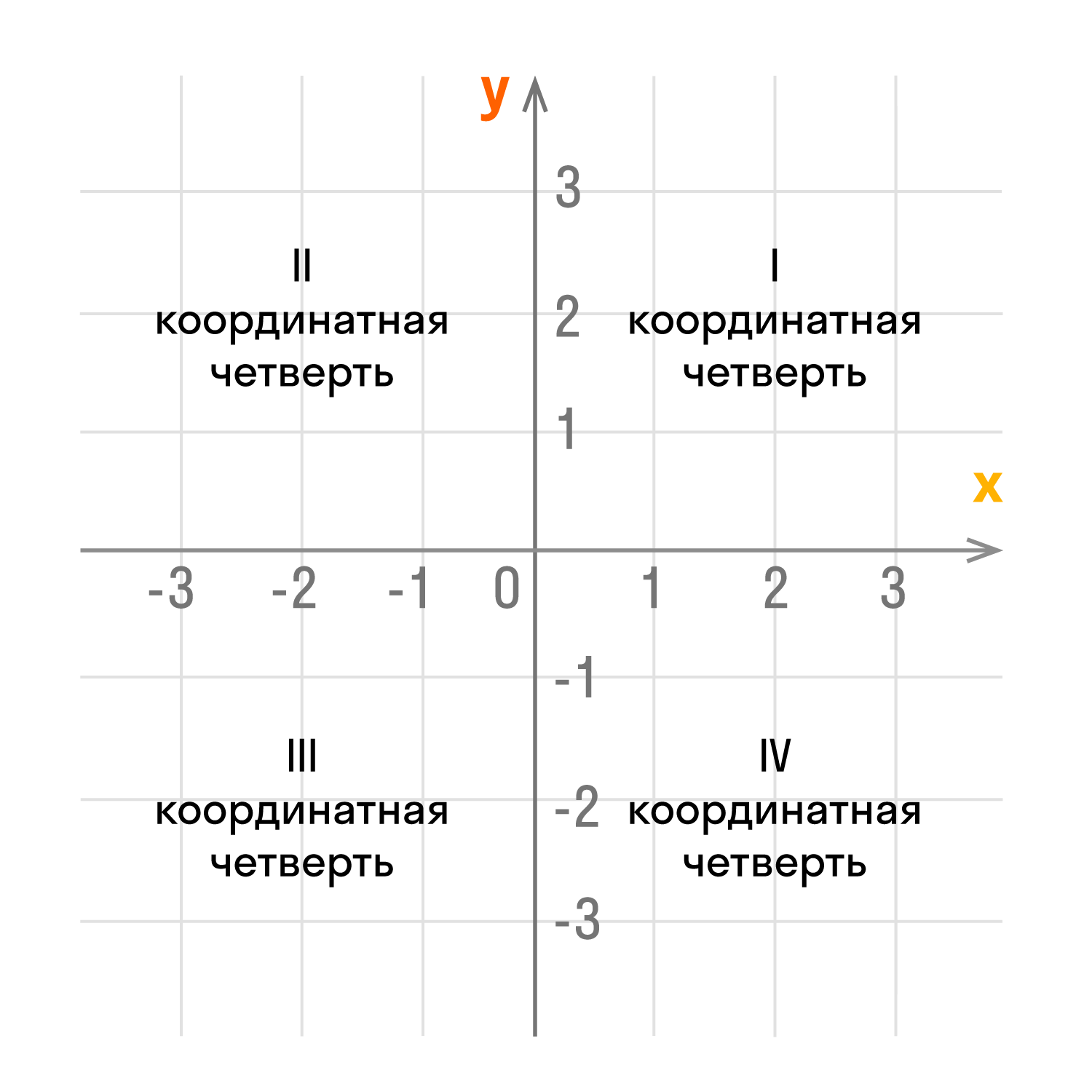
Чтобы узнать координаты точки в прямоугольной системе координат, необходимо опустить перпендикуляр от точки к каждой оси и посчитать количество единичных сегментов от нулевой отметки до освобожденного перпендикуляра. В скобках записаны координаты, первая по оси Ox, вторая по оси Oy.

Согласованные правила:

• Если обе координаты положительны, точка находится в первой четверти координатной плоскости.
• Если координата x отрицательна, а координата y положительна, то точка находится во второй четверти.
• Если обе координаты отрицательны, число находится в третьей четверти.
• Если координата x положительна, а координата y отрицательна, точка находится в четвертой четверти.

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Способы задания положения точки и описание ее движения — Кинематика — МЕХАНИКА

1.1. Кинематика

1.1.5. Способы задания положения точки и описание ее движения

Положение точки в пространстве задается двумя способами:

1) с помощью координат; 2) с помощью радиус-вектора.

Положение точки с помощью координат задается тремя проекциями точки х, у, z на оси декартовой системы координат ОХ, ОУ, ОZ, связанные с телом отсчета (рис. 1.3). Для этого из точки А необходимо опустить перпендикуляры на плоскости УZ (координата х), ХZ (координата у), ХУ (координата z) соответственно. Записывается это так: А (х, у, z). Для конкретного случая, изображенного на рис. 1.3 (х = 6, у = 10, z = 4,5), точка А обозначается A (6; 10; 4,5).

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси (х на ось ОХ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат О и лежащая на диагонали параллелепипеда, и будет искомой точкой А.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: ОХ и ОУ. Тогда положение точки на плоскости определяют двумя координатами х и у (рис. 1.4).

Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.

Задание положения точки А с помощью радиус-вектора осуществляется соединением точки А с началом координат О (рис. 1.4). Направленный отрезок О А =

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций rх, ry, rz на оси координат ОХ, ОУ, OZ, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 1.4) имеем:

Здесь r =

х
y

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор г можно также разложить на составляющие по осям X и У, т. е. представить в виде суммы двух векторов (рис. 1.4):

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус- вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).

Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называетсяпрямолинейным, а если кривая — криволинейным.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Нестандартные углы и периодичность

До сих пор мы рассматривали углы ∈ . Но что произойдет, если, например, угол = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.

Итак, что если угол > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).

С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол ∈ . Таким образом, вся схема решения выглядит следующим образом:

1. Перейти от радианной меры угла к градусной. Для этого достаточно сделать замену: → 180°;
2. Если полученный угол оказался больше 360°, отнимаем от него по 360° до тех пор, пока новый угол не окажется на отрезке ;
3. Аналогично, если угол будет отрицательным, увеличиваем его на 360° до тех пор, пока он не попадет в отрезок ;
4. Выясняем, в какой координатной четверти находится полученный угол, ориентируясь на стандартные границы: 90°, 180°, 270° и 360°.

Снова переводим все углы из радиан в градусы по правилу: → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке . И только затем выясняем координатную четверть. Получим:

1. sin 21/6 = sin (23 · 180/6) = sin 690°. Очевидно, что 690° > 360°, поэтому выполняем преобразование: sin 690° → sin (690° − 360°) = sin 330°. Но 330° ∈ , это IV четверть;
2. cos 19/3 = cos (19 · 180/3) = cos 1140°. Поскольку 1140° > 360°, имеем: cos 1140° → cos (1140° − 360°) =cos 780° → cos (780° − 360°) =cos 420° →cos (420° − 360°) = cos 60°. Т.к. 60° ∈ , это I четверть;
3. sin (−7/9) = sin (−7 · 180/9) = sin (−140°). Но −140° < 0°, поэтому увеличиваем угол: sin (−140°) →sin (−140° + 360°) = sin 220°. Поскольку 220° ∈ , это III четверть;
4. tg (−11/4) = tg (−11 · 180/4) = tg (−495°).Т.к. −495° < 0°, начинаем увеличивать угол: tg (−495°) →tg (−495° + 360°) =tg (−135°) →tg (−135° + 360°) = tg 225°. Это уже нормальный угол. Т.к. 225° ∈ , это III четверть.

Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол

Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать.

В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную.

Системы координат

Под понятием координат в повседневной жизни понимается упорядоченный набор слов, цифр и прочих знаков, позволяющий определить местоположение человека, здания или другого объекта. Эти знания необходимы для ориентирования в современном обществе и организации любой человеческой деятельности.

Примеры использования:

• почтовый адрес;
• номер места в театре, автобусе или самолёте;
• обозначение положения фигур на шахматной доске;
• географическая широта и долгота.

Таким образом, система координат необходима не только в математике.

Она буквально пронзает всю человеческую жизнь.

Без применения этих научных знаний люди не смогли бы значительно отдалиться от животных и первобытных предков.

Некоторые области применения:

1. Геометрия довольно часто пользуется методикой нахождения точки на координатной плоскости или в пространстве.
2. Математика — построение графиков функций.
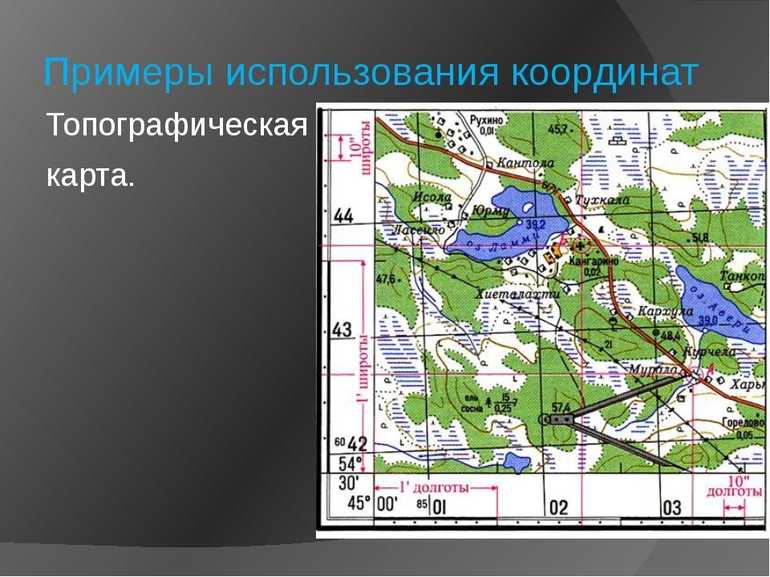
3. География использует собственные координаты (широта и долгота).
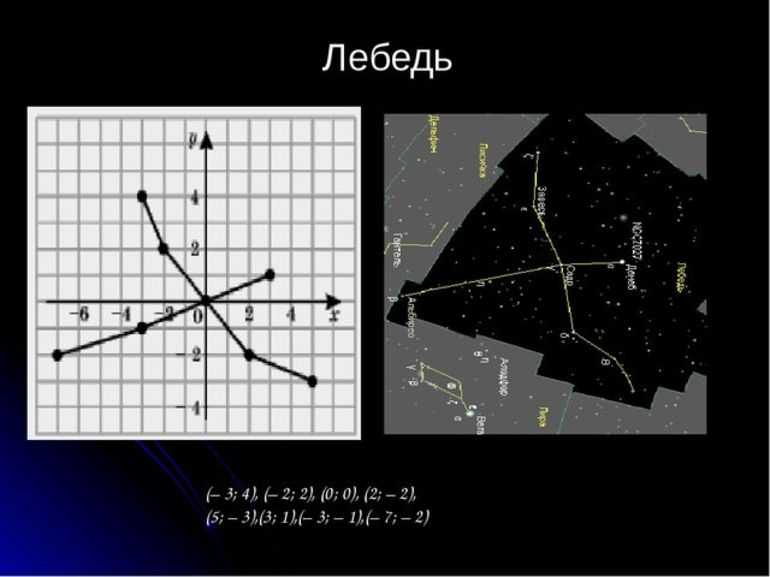
4. Астрономия определяет положение небесных объектов во вселенной.

По определению любая координатная система представляет собой ряд идентификационных данных, которые позволяют узнать положение точки или фигуры в пространстве, а также дают возможность проследить её перемещение.

Наибольшее распространение получила прямоугольная система координат, которую ещё называют декартовой, по имени создателя Рене Декарта. Её популярность основана на простоте и универсальности.

Другие виды координат:

• полярные;
• цилиндрические;
• сферические;
• косоугольные;
• биангулярные;
• биполярные;
• конические;
• бицентрические;
• координаты Риндлера;
• бицилиндрические;
• параболические;
• тороидальные;
• проективные;
• трилинейные;
• эллипсоидальные.

https://youtube.com/watch?v=cb1xbqsROq8