Дайте определение системы отсчета. раздел i. физические основы механики

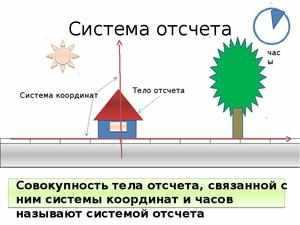
Основные составляющие

Основными составляющими любой системы отсчёта в механике можно считать следующие компоненты:

1. Тело отсчёта – это физическое тело, по отношению к которому определяется изменение положения в пространстве других тел.
2. Совокупность координат, которая связывается с этим телом. В этом случае она представляет собой точку отсчёта.
3. Время – это момент начала отсчитывания времени, который необходим, чтобы определить нахождение тела в пространстве в любой момент.

Для того чтобы решить конкретную задачу, необходимо определить наиболее подходящую для этого сетку координат и структуру. Идеальные часы в каждой из них потребуются лишь одни. В этом случае начало, тело отсчёта и векторы координатных осей можно выбирать произвольно.

Разновидности движения

Механическое движение, осуществляемое твёрдым телом, считается поступательным в том случае если отрезок, соединяющий две любые точки тела, находящегося в любой точке траектории, остаётся параллельным и неизменным по величине относительно отрезка соединяющего эти же его точки в начальной точке траектории. Примером поступательного движения может служить поднимающаяся или опускающаяся кабина лифта, либо кабина, установленная на колесе обозрения.

Траектория является важным параметром, характеризующим движение. По сути это пространственная кривая, нередко имеющая вид сопряжённых дуг, обладающих своим центром и соответствующим радиусом. Положение центра траектории для разных точек тела отличается и способно меняться с течением времени.

Хотя поступательное движение может осуществляться в 3-х мерном пространстве, тем не менее, главной его отличительной особенностью остаётся сохраняемая параллельность любого отрезка по отношению к самому себе в любой точке траектории.

Движение материальной точки по траектории, имеющей форму окружности, называется вращательным движением. Все точки абсолютно твёрдого тела, совершающего вращательное движение, перемещаются по окружностям, находящимся на параллельных плоскостях. Центры этих окружностей располагаются на одной прямой, перпендикулярно расположенной к плоскостям, на которых они лежат, именуемой осью вращения. Она может находиться как внутри движущегося тела, так и за его пределами.

Период обращения, обозначаемый буквой T, представляет собой время, в течение которого тело совершает полный оборот. Он определяется путём деления времени Δt, на протяжении которого осуществлялось вращение, на количество оборотов N:

T=Δt/N.

В системе возможно неподвижное и подвижное состояние оси вращения. К примеру, ось вращения установленного на электростанции генератора находится в неподвижном состоянии относительно связанной с Землёй системы координат.

В некоторых случаях ось вращения совершает сложное вращение, заставляя точки тела двигаться по сферическим траекториям. Подобное движение называется сферическим. Перемещение материальной точки или тела вокруг оси находящейся в неподвижном состоянии за его пределами носит название движения кругового.

Базовыми характеристиками прямолинейного движения являются: скорость, перемещение, ускорение. Для движения вращательного аналогичными показателями являются:

• угловое перемещение – в роли перемещения, в случае с вращательным движением, выступает угол;
• угловая скорость – характеризующая величину угла, на который выполнен поворот, за единицу времени;
• угловое ускорение – представляющее собой изменение угловой скорости, происходящее в определённый временной промежуток.

Основные принципы физического отсчета

Одним из основных принципов физического отсчета является выбор тела отсчета. Тело отсчета — это объект, который выбирается физиком и относительно которого происходит измерение и описание явлений. Например, при изучении движения автомобиля величиной отсчета может быть время, пройденное автомобилем, или расстояние, пройденное автомобилем от его начальной точки.

Другим важным принципом физического отсчета является выбор начала отсчета. Начало отсчета — это точка, относительно которой измеряются величины. Например, при измерении времени, началом отсчета может быть момент старта секундомера или начало какого-либо события.

Третий принцип физического отсчета — выбор единицы измерения. Единица измерения — это определенная величина, которая используется для измерения других величин. Например, при измерении длины в системе СИ, единицей измерения является метр. Выбор единицы измерения является важным, так как он позволяет установить соотношение между измеряемыми величинами и позволяет сравнивать результаты измерений.

Еще одним принципом физического отсчета является определение направления положительного и отрицательного движения. Направление положительного движения может быть произвольным, но оно должно быть четко определено и согласовано с выбранным телом отсчета. Например, при изучении движения автомобиля, можно выбрать направление движения автомобиля вперед как положительное, а движение назад — отрицательное.

Таким образом, основные принципы физического отсчета включают выбор тела отсчета, выбор начала отсчета, выбор единицы измерения и определение направления положительного и отрицательного движения. Эти принципы позволяют проводить измерения, описывать явления и анализировать результаты в физике.

Колебательное движение

Выполнение периодических перемещений в двух противоположных друг другу направлениях называется колебательным движением. Процесс колебаний, происходящих в замкнутых системах, именуется колебаниями собственными или независимыми. Колебательные движения, вызываемые под воздействием сил приложенных из вне, являются колебаниями вынужденными.

Использование для анализа колебаний изменяемых показателей, таких как частота, амплитуда, период и др. позволило разделить их на колебания гармоничные, затухающие и нарастающие. Кроме этого они могут быть сложными, прямоугольными, пилообразными.

В случае свободных колебаний происходящих в действительных системах неизбежно происходят потери энергии. Затраты энергии связаны с преодолением сил сопротивления воздуха и сил трения снижающих амплитуду колебаний и способных окончательно их прекратить по прошествии некоторого времени.

Вынужденные колебания не являются затухающими по причине постоянного восполнения потерь энергии, происходящего на протяжении всего времени колебаний. Это осуществляется путём периодического воздействия на тело силой разной величины. Частота вынужденных колебаний пропорциональна изменениям, прилагаемой внешней силы.

Максимальное значение амплитуды вынужденных колебаний достигается при совпадении их частоты с собственной частотой колебательной системы. Данный процесс называется резонансом.

К примеру, амплитуда раскачивания каната будет постоянно увеличиваться в случае периодического подталкивания его в такт с его собственными колебаниями.

Тело, размерами которого можно в определённых условиях пренебречь, называется материальной точкой.

Рассматриваемый выше автомобиль может быть принят в качестве материальной точки, если его рассматривать в сравнении с Землёй. Однако пренебречь размерами машины невозможно в случае рассмотрения перемещения людей, находящихся внутри неё.

Задачи, решаемые в физике, подразумевают расценивание движения, выполняемого телом, как движение, осуществляемое материальной точкой, применяя для анализа такого движения такие понятия как скорость, ускорение, инерция материальной точки и т.д.

Не нашли ответ?
Просто напиши,с чем тебе нужна помощь

Мне нужна помощь

Механическое движение

Механическим движением называется изменение положения тела (или какой-либо его части) по отношению к другому телу (телам).

Примером такого движения может быть спускающийся или поднимающийся на эскалаторе в метро человек. Находясь в состоянии покоя относительно самого эскалатора, человек всё же перемещается по отношению к стенам туннеля. По такому же принципу гора Эльбрус пребывает в состоянии покоя относительно планеты Земля, всё же движется вместе с ней по отношению к Солнцу.

Из приведённых выше примеров видно, что для изучения перемещений, прежде всего, необходимо определить точку (в дальнейшем называемую точкой отсчёта), по отношению к которой оно будет рассматриваться. Данная точка, связанная с ней система координат и определённый метод замера времени являются составляющими системы отсчёта. Поступательным движением тела называется его перемещение относительно точки отсчёта, причём, все принадлежащие ему точки перемещаются одновременно. Скорость движения тела V определяется по средствам деления пройденного им пути S на величину временного отрезка T, в течение которого оно происходит:

V=S/T.

В качестве примера поступательного движения можно рассмотреть перемещающийся по дороге автомобиль. Однако поступательно в этом случае движется исключительно кузов автомобиля, поскольку его колёса во время перемещения по дороге постоянно выполняют вращательное движение.

Вращательным движением называется движение, совершаемое вокруг какой-либо оси. Данный тип движения характеризуется перемещением всех точек, принадлежащих телу, по замкнутой траектории, центром которой является эта ось. Возвращаясь к примеру с автомобилем можно сделать вывод о том, что колёса, совершающие вокруг своей оси вращательные движения, одновременно движутся поступательно вместе с автомобильным кузовом. Таким образом, в отношении оси колёса осуществляют вращательное движение, а по отношению к дорожному полотну – движутся поступательно.

Периодическое перемещение, поочерёдно совершаемое телом в противоположных двух направлениях, получило название движения колебательного. Простейшим примером подобного движения является перемещение маятника часов.

Самыми простыми видами движения являются движения поступательные и движения вращательные.

В случае, когда точка X изменяет своё положение по отношению к точке Y, одновременно происходит изменение положения точки Y в отношении точки X. Другими словами движение обеих точек происходит друг относительно друга. Относительным считается такое механическое движение, при котором его описание требует определения точки, относительно которой будет рассматриваться данное движение.

К простым типам движения, осуществляемым материальной точкой, относятся перемещения, выполняемые равномерно и перемещения по прямолинейной траектории. Движение считается равномерным в том случае, когда модуль вектора, характеризующего скорость, остаётся неизменным, направление при этом может изменяться.

Прямолинейным называют движение, при котором неизменным остаётся направление вектора скорости, в то время как его величина способна изменять своё значение. Линия, на которой располагается вектор скорости, именуется траекторией.

В повседневной жизни человек постоянно сталкивается с многочисленными примерами механического движения – это и движущиеся мимо автомобили, проплывающие корабли и летящие самолёты и т.п. Простейшие примеры формируются самими людьми, проходящими около других людей. Наша планета каждую секунду осуществляет движение двух видов: вокруг собственной оси и вокруг Солнца, что, по сути, тоже является примером механического движения.

Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь

Мне нужна помощь

Типы механического движения

Механическое движение бывает трех основных типов:

• прямолинейное движение;
• равномерное движение;
• криволинейное движение.

Для решения задач в физике принято использовать допущения в виде представления объекта материальной точкой. Это имеет смысл в тех случаях, когда форму, размер и тело можно не учитывать в его истинных параметрах и выбрать изучаемый объект в виде определенной точки.

Существует несколько основных условий, когда применяется в решении задачи метод внедрения материальной точки:

• в случаях, если размеры тела чрезвычайно малы по отношению к расстоянию, которое оно проходит;
• в случаях, если тело двигается поступательно.

Поступательное движение возникает в момент, когда все точки материального тела движутся одинаково. Также тело будет двигаться поступательным образом, когда через две точки этого объекта проведут прямую, и она должна смещаться параллельно первоначальному месторасположению.

При начале изучения относительности механического движения вводят понятие системы отсчета. Она образуется вместе с телом отсчета и системой координат, включая часы для отсчета времени движения. Все элементы составляют единую систему отсчета.

Виды систем отсчёта

Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.

Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.

Инерциальные системы отсчёта

Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.

1. Существование таких совокупностей подчиняется первому закону Ньютона.
2. Именно в таких сетках возможно наиболее простое описание движения тел.
3. По существу, инерциальная структура — это всего лишь идеальна математическая модель. Найти такую структуру в физическом мире не представляется возможным.

Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.

Неинерциальные системы отсчёта

Неинерциальные разновидности наравне с инерциальными связываются с планетой Земля. Учитывая космические масштабы, считать Землю инерциальной совокупностью можно весьма грубо и приблизительно.

Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.

Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.

Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.

Основные свойства

Эти структуры в физике и геометрии имеют ряд существенных различий. К физическим свойствам, которые учитываются при построении и решении задачи, относятся изотропность и однородность.

Под однородностью в физике принято понимать тождественность всех точек в пространстве

Этот фактор имеет в физике немаловажное значение. Во всех точках Земли и Солнечной системы в целом законы Ньютона в физики действуют абсолютно идентично

Благодаря этому начало отсчёта может быть размещено в любой удобной точке. И если исследователь поворачивает сетку координат вокруг начальной точки, при этом никакие другие параметры задачи не будут изменяться. Все направления, которые начинаются от этой точки, имеют абсолютно тождественные свойства. Такая закономерность называется изотропностью пространства.

Особенности применения, примеры из жизни

Для того чтобы правильно и понятно провести описание движения тела, необходимо знать, как описать его положение в пространстве, а следовательно — выбрать систему отсчета.

Согласно закону относительности движения, свойства движущегося тела определяются тем, относительно каких тел рассматривается само движение, какая шкала отражает его цифровые значения.

При определении положения материальной точки относительно выбранной системы отсчета необходимо грамотно высчитать промежуток времени, в течение которого происходит движение. Это можно сделать только с помощью часов, которые позволяют использовать единицы измерения в секундах с точностью до тринадцатого знака после запятой.

Для подтверждения того, насколько важно правильно выбрать систему отсчета для характеристики нахождения предмета, рассмотрим примеры:

1. Человек поднял руку вверх. По отношению к ногам рука совершила движение, отдалившись от ноги на определенное количество см. Однако по отношению к пуговице на рукаве этой же руки никакого изменения положения не произошло.
2. Человек переставил стул с одного места в комнате на другое. Приняв за точку отсчета окно, стул переместился на определенное расстояние. Однако, описывая его перемещение относительно одной из ножек стула, оно равно нулю.

В качестве эталона ответа на вопрос об относительности движения часто приводят задачу о нашей планете. С давних времен идут споры о том, вращается ли Земля вокруг Солнца или Солнце — вокруг Земли. Объективно, с позиции положений теории о механическом движении, следует рассматривать спор о выбранном теле отсчета.

При рассмотрении в его качестве Земли, Солнце производит вокруг него вращательное движение. Если за тело отсчета принять Солнце, то вращательные движения производит Земля (вокруг Солнца и вокруг собственной оси).

Из этого примера понятно, насколько важно в начале решения поставленной задачи определиться с точкой отсчета. Разнообразие выбора системы отсчета влияет не только на оценку, движется тело или нет

От этого зависит форма траектории и пройденный путь.

Математические модели, используемые для тела отсчета

Одной из основных математических моделей, используемых для тела отсчета, является модель точечной частицы. В этой модели предполагается, что физическое тело представляется невесомой и бесконечно малой точкой, не имеющей размеров и формы. Такая модель позволяет легче работать с объектами и учитывать только их массу и положение в пространстве.

Кроме того, для описания движения тела отсчета используются математические модели, основанные на физических законах. Например, закон Ньютона о движении позволяет определить взаимодействие тела с другими объектами и рассчитать силу, ускорение и скорость тела отсчета.

Еще одной важной математической моделью является модель гармонического колебания. Она используется для описания периодических движений, таких как колебания маятника или звуковых волн

В модели предполагается, что тело отсчета движется вокруг положения равновесия и подчиняется закону Гука, который определяет зависимость между силой и смещением.

Математические модели позволяют упростить сложные физические явления и получить численные значения для различных величин. Это делает их неотъемлемой частью изучения и применения тела отсчета в физике.

Механическое движение

При рассмотрении движения тела в физике вводится несколько упрощений, которые позволяют выявить основные закономерности и описать их математически. Одно из таких упрощений — рассмотрение тела как точки. Это возможно в том случае, когда размеры тела пренебрежительно малы по сравнению с изменениями его пространственного положения.

Траектория движения точки (тела) — линия, которую описывает в пространстве точка во время движения. При неподвижной точке траектория движения сама превращается в точку.

Путь — это расстояние между двумя положениями точки, измеренное вдоль траектории ее движения.

Движение тела или точки может характеризоваться не только величиной, но и направлением. Такие характеристики называются векторными или просто векторами. Перемещение — это вектор, соединяющий начальное и конечное положение точки. Направление и величина перемещения определяются отрезком прямой между начальной и конечной точками движения.

Скорость. Механическое движение характеризуется еще и тем, насколько быстро движется точка (тело). Эта характеристика называется скорость движения. Скорость — величина векторная. Для того, чтобы полностью задать ее, надо задать собственно величину скорости и направление, вдоль которого она измерена. Обычно рассматривается скорость тела вдоль траектории его движения. Тогда величина скорости определяется как путь, пройденный в единицу времени. Иначе говоря, для того, чтобы найти скорость вдоль траектории движения надо путь разделить на время, за которое он был пройден.

Формулы для решения:Пусть v — скорость, s — путь, t — время. Скорость измеряется вдоль траектории движения. Тогда:
$$ \vec{V}=\frac{\vec{S}}{\vec{t}} $$
Перемещение определяется как геометрическая сумма отрезков пути. Для простейшего случая, когда один участок пути направлен перпендикулярно другому решается прямоугольный треугольник:

\(l=\sqrt{S_1^2 + S_2^2}\)

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени. К примеру, автобус по отношению к людям. Потому что, к примеру, относительно людей, которые едут в автобусе, механическое движение не совершается.

В более общем значении движением называется изменение состояния физической системы с течением времени. Например, можно говорить о движении волны в среде.

Виды механического движения:

1. движение материальной точки;
2. движение твердого тела;
3. движение сплошной среды.

Механическое движение может быть прямолинейным или криволинейным, равномерным или неравномерным.

На какие виды делится механическое движение по типу траектории?

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Поступательное и вращательное движения – самые простые виды механического движения.

«Механическое движение. Траектория и путь»

Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Изучение механики традиционно начинают с кинематики.

Кинематика — раздел механики, в котором рассматривают способы описания механического движения тел без выяснения причин изменения характера их движения. Сами причины рассматриваются в других разделах механики.

Траектория движения — это линия, вдоль которой движется тело.

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец — с конечным положением точки. Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь — это длина траектории, пройденной телом. Путь — всё расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения. Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и модуля перемещения тела, и модуля изменения координаты тела.

Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).

Виды траекторий. Если тело движется вдоль прямой, движение называют прямолинейным. Траектория в этом случае — отрезок прямой. Если же траектория — кривая линия, движение называют криволинейным.

Относительность движения

Для того чтобы описать положение данного тела в пространстве, необходимо:

1. выбрать тело отсчёта и начало отсчёта на нём;
2. связать с ним координатную ось, проходящую через начало отсчёта в нужном направлении, и указать единицу длины.

При этом расстояние от начала отсчёта до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.

https://youtube.com/watch?v=Vz3tdk7zT1s

Система отсчета

Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчёта. Если мы выберем в качестве тела отсчёта другое тело или другую ось координат, то и координата данного тела может стать другой. Совокупность тела отсчёта, с которым связана ось координат, и часов называют системой отсчёта.

Если координата тела не изменяется с течением времени в выбранной системе отсчёта, то говорят, что это тело в данной системе отсчёта неподвижно, или покоится.

Если координата тела выбранной системы отсчёта увеличивается со временем, то говорят, что тело движется в положительном направлении координатной оси. Напротив, если координата тела в выбранной системе отсчёта со временем уменьшается, то говорят, что тело движется в отрицательном направлении координатной оси.

Нельзя сказать, как движется тело, если не сказать, в какой системе отсчёта рассматривается это тело. Иначе говоря, одно и то же тело в разных системах отсчёта может двигаться по-разному (в том числе и покоиться).

Конспект по физике в 7 классе по теме «Механическое движение. Траектория».

Следующая тема: Прямолинейное равномерное движение

Развитие относительности механического движения

Также согласно закону инерции, стали формировать инерциальные системы отсчета.

Процесс осознания относительности механического движения занял немалый исторический промежуток времени. Если сначала долгое время считалась приемлемой модель геоцентрической системы мира (Земля – центр Вселенной), то движение тел в разных системах отсчета стали рассматривать во времена известного ученого Николая Коперника, который сформировал гелиоцентрическую модель мира. Согласно ей, планеты Солнечной системы совершают вращение вокруг Солнца, а также совершают вращения вокруг собственной оси.

Поменялась структура системы отсчета, что привело позже к построению прогрессивной гелиоцентрической системы. Эта модель сегодня позволяет решать различные научные цели и задачи, в том числе в сфере прикладной астрономии, когда просчитывается траектории движения звезд, планет, галактик, исходя из метода относительности.

В начале 20 века была сформулирована теория относительности, которая также базируется на основополагающих принципах механического движения и взаимодействия тел.

Все формулы, которые применяются для высчитывания механических движений тел и определения их скорости, имеют смысл на скоростях меньше скорости света в вакууме.

ОПРЕДЕЛЕНИЕ

Относительность движения
проявляется в том, что поведение любого движущегося тела может быть определено только по отношению к какому-то другому телу, которое называют телом отсчета.

Примеры использования тела отсчета

1. В механике тело отсчета может быть выбрано в качестве точки отсчета для измерения позиции и перемещения объекта. Например, чтобы измерить расстояние, пройденное автомобилем, тело отсчета может быть установлено на одной конечной точке и измерять позицию автомобиля относительно этой точки.

2. В электричестве и магнетизме тело отсчета может быть положено в центре заряженного объекта или магнитного поля для измерения его величины. Например, тело отсчета может быть установлено в центре заряженного шарика для измерения его электрического поля.

3. В термодинамике тело отсчета может быть выбрано для определения температуры и измерения изменений в ней. Например, тело отсчета может быть установлено в некоторой точке в сосуде с газом для измерения его температуры и изменения при нагревании или охлаждении.

4. В оптике тело отсчета может быть выбрано для определения фокусного расстояния линзы или измерения отражения и преломления света. Например, тело отсчета может быть установлено в фокусной плоскости линзы для измерения ее фокусного расстояния.

Это лишь некоторые примеры использования тела отсчета в физике. Оно является неотъемлемой частью измерений и анализа физических явлений, помогая физикам понять и описать мир вокруг нас.

Принципы работы системы отсчета

Система отсчета в физике представляет собой универсальный инструмент, который позволяет описывать и измерять различные физические явления. Основными принципами работы системы отсчета являются точность, стандартизация и простота использования.

1. Точность

Одним из важнейших принципов работы системы отсчета является достижение высокой точности измерений. Это достигается путем использования стандартных единиц измерения и точных методов измерений. Точность измерений является основой для получения достоверных данных и дальнейшего анализа физических явлений.

2. Стандартизация

Система отсчета основана на установленных стандартах, которые определяют единицы измерения и методы их определения. Стандартизация позволяет обеспечить единообразие и согласованность в измерениях, что является ключевым фактором для обмена информацией и сравнения результатов между различными научными лабораториями и исследователями.

3. Простота использования

Система отсчета должна быть проста в использовании и понятна для пользователей. Единицы измерения должны быть логичными и удобными в применении, а методы измерений – доступными и понятными. Простота использования системы отсчета позволяет легко проводить измерения и анализ физических процессов без ошибок и сложностей.

Цилиндрическая и сферическая системы координат

Декартова система координат обеспечивает простой способ описания расположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Рассмотрим два разных способа описания положения точек в пространстве, оба из которых основаны на расширениях полярных координат. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами, таких как расчет объема круглого резервуара для воды или количества масла, протекающего по трубе. Точно так же сферические координаты полезны для решения задач, связанных со сферами.

Цилиндрическая система координат

Когда мы расширили традиционную декартову систему координат с двух измерений до трех, мы просто добавили новую ось для моделирования третьего измерения. Начиная с полярных координат, мы можем следовать тому же процессу, чтобы создать новую трехмерную систему координат, называемую цилиндрической системой координат. Таким образом, цилиндрические координаты обеспечивают естественное расширение полярных координат до трех измерений.

В цилиндрической системе координат точка в пространстве (рис. 3) представлена ​​упорядоченными тремя скалярами \ где \ полярные координаты проекции точки на плоскость \, а z-координата в декартовой системе координат.

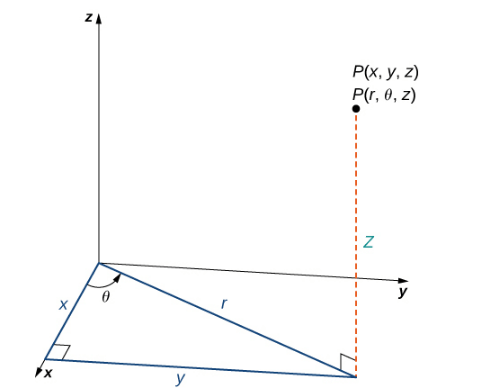Рис. 3 Правый треугольник лежит в плоскости xy

Длина гипотенузы равна r и θ — мера угла, образованного положительной осью x и гипотенузой. Г координата описывает местоположение точки выше или ниже х плоскости.

На плоскости xy прямоугольный треугольник, показанный на рис. 3, дает ключ к преобразованию между цилиндрическими и декартовыми (прямоугольными) координатами.

Преобразование между цилиндрическими и декартовыми координатами

Прямоугольные координаты (x,y,z)  и цилиндрические координаты  (r,θ,z)  точки связаны следующим образом:

\
\ — уравнения для преобразования из цилиндрических координат в декартовые

\ и \

\ — уравнения для преобразования из декартовых в цилиндрические

\

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Применение тел отсчета в научных исследованиях

В научных исследованиях тело отсчета играет ключевую роль при изучении различных физических процессов и явлений. Оно помогает определить положение, скорость, ускорение и другие параметры объектов в пространстве и времени.

Применение тел отсчета позволяет установить точную связь между наблюдаемыми явлениями и их физическими характеристиками. Оно позволяет проводить измерения с высокой точностью и воспроизводимостью результатов.

Принципиальное применение тел отсчета можно наблюдать в механике, где они служат основой для построения математических моделей движения тел. С помощью указанных тел можно описывать и предсказывать траектории движения объектов, а также исследовать взаимодействия между ними.

Кроме того, тела отсчета используются в различных областях физики, таких как электродинамика, термодинамика, оптика и астрономия. Они служат основой для проведения экспериментов, измерения физических величин и получения новых научных данных.

Таким образом, применение тел отсчета в научных исследованиях является неотъемлемой частью работы физиков и других ученых. Они позволяют получать точные и объективные данные о физических явлениях, расширяют наши знания о природе мира и служат основой для развития новых технологий и открытий.