Материальная точка. система отсчета

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Простейшей формой изменения является механическое движение. Механическое движение — это изменение положения одного тела по отношению к другому телу в пространстве с течением времени.

А наука о законах механического движения и причинах этого движения называется механикой.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Материальная точка. Система отсчета»

Механику обычно делят на два раздела: кинематику, которая отвечает на вопрос, как движутся тела, и динамику, которая исследует причины и выясняет, почему тела движутся так, а не иначе.

Изучение механики начинается с кинематики, потому что понятия кинематики составляют основу всей физики.

Кинематика — это раздел механики, изучающий движение тел без рассмотрения причин этого движения.

Основная задача кинематики — определить положение тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

В седьмом классе вы узнали о самом простом виде движения — линейном. На самом деле, движение тел может быть очень сложным: посмотрите на аэроплан, выполняющий трюки…..

Как кинематика может описать такие сложные движения?

Дело в том, что кинематика позволяет представить любое сложное движение как состоящее из трех основных движений.

Все вы знаете, что в данный момент времени каждое тело принимает определенную геометрическую форму, определенную ориентацию в пространстве и определенное положение в пространстве. Давайте проведем простой эксперимент с простым ластиком. Он может гнуться, то есть менять свою форму. Его можно поворачивать, то есть по-разному ориентировать по отношению к столу. И наконец, ластик можно переместить в другую точку без изменения его формы и ориентации в пространстве.

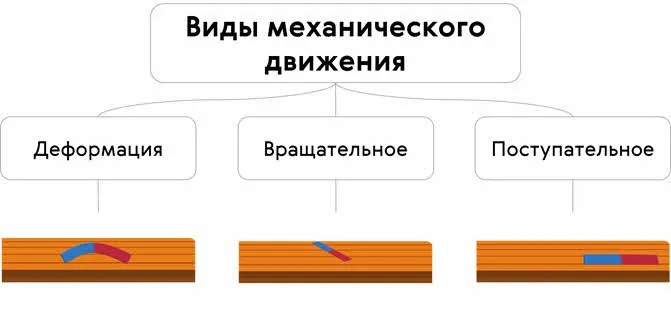
Поэтому и форма, и ориентация в пространстве, и положение тела могут меняться с течением времени. И каждое из этих изменений соответствует одному из трех основных типов механического движения — деформация…, вращательное движение…. и поступательное движение…

Вы знакомы с деформацией тела. Это процесс изменения формы

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег участвовали в курсах «Инфорурок»).

В настоящее время существует накопительная скидка (от 2% до 25%) для 54 669 школ и колледжей. Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет InforoLesson.

2 слайд Что такое инженерия движения? Что такое траектория? Что такое равномерное движение? Что такое поступательное движение? Что такое скорость тела? Как можно определить скорость тела, если известны расстояние и время? Отзыв.

3 слайд Механическое движение Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

4 Слайд Траектория Траектория — это линия, описываемая движущимся телом.

5 Слайд Равномерное движение Движение с постоянной скоростью.

6 Слайд Поступательное движение Тело движется равномерно, если все его точки движутся равномерно.

Теория и методика педагогического проектирования

7 слайд Скорость тела Скорость — это физическая величина, которая описывает, как быстро изменяется скорость тела.

8 Слайд Что такое материальная точка? Всегда ли можно применять термин «материальная точка»? Что такое система отсчета? Из чего состоит система отсчета?

Материальная точка Система отсчета

«Инновация. Инновационные технологии»

Слайд 9 При решении различных научных и практических задач, связанных с механическим движением тел, необходимо уметь описывать движение

10 Слайд 10 Описать движение тела Определить траекторию движения Определить скорость движения Определить расстояние, пройденное телом Определить положение тела в пространстве и т.д.

Равномерное линейное движение — это движение, при котором материальная точка, движущаяся по прямой, проходит путь равной длины через случайные равные промежутки времени.

Примером равномерного линейного движения является движение сборочной линии на заводе, движение поезда по прямой линии с постоянной тягой и т.д.

Однако следует помнить, что в природе не существует идеально равномерного движения, но если отклонения от равномерности незначительны, ими можно пренебречь.

Физическая величина, численно соответствующая расстоянию, пройденному телом за единицу времени, называется скоростью u.

Для описания движения тела вводится векторная физическая величина — скорость. Положение тела, движущегося по прямой линии в момент времени t

определяется s

и в момент времени t — s. Тогда в момент времени t — t

тело движется на расстояние s — s

Уроки арифметики на русском языке

• Урок №2. Сложение натуральных чисел
• Урок №3. Вычитание натуральных чисел
• Урок №4. Таблица умножения
• Урок №5. Умножение натуральных чисел
• Урок №6. Деление натуральных чисел
• Урок №8. Величины и их измерение
• Урок №10. Делимость чисел
• Урок №13. Обыкновенные дроби
• Урок №15. Сложение дробей
• Урок №16. Вычитание дробей
• Урок №17. Умножение дробей
• Урок №18. Деление дробей
• Урок №21. Конечные десятичные дроби
• Урок №22. Сложение десятичных дробей
• Урок №23. Вычитание десятичных дробей
• Урок №24. Умножение десятичных дробей
• Урок №25. Деление десятичных дробей
• Урок №26. Округление чисел
• Урок №1. Отношение величин
• Урок №2. Пропорции
• Урок №6. Проценты
• Урок №7. Нахождение процентов данного числа
• Урок №12. Среднее арифметическое
• Урок №14. Масштаб

Уроки арифметики на українській мові

• Урок №2. Додавання натуральних чисел
• Урок №3. Віднімання натуральних чисел
• Урок №4. Таблиця множення
• Урок №5. Множення натуральних чисел
• Урок №6. Ділення натуральних чисел
• Урок №8. Величини та їх вимірювання
• Урок №10. Подільність чисел
• Урок №13. Звичайні дроби
• Урок №15. Додавання дробів
• Урок №16. Віднімання дробів
• Урок №17. Множення дробів
• Урок №18. Ділення дробів
• Урок №21. Кінечни десяткові дроби
• Урок №22. Додавання десяткових дробів
• Урок №23. Віднимання десяткових дробів
• Урок №24. Множення десяткових дробів
• Урок №25. Ділення десяткових дробів
• Урок №18. Нескінченний десятковий дріб
• Урок №19. Відношення величин
• Урок №20. Пропорції
• Урок №6. Відсотки
• Урок №7. Відсотки (2)
• Урок №12. Середнє арифметичне
• Урок №14. Масштаб

ВИДЕО УРОК

1. В каком случае тело можно считать
материальной точкой?

1 –
на станке изготовляют спортивный диск;

2 –
диск после броска спортсмена пролетает
расстояние в55 м.

а)в
первом; б);

в) во
втором; г).

2. В каком случае тело можно считать
материальной точкой?

1 –
пассажирский самолёт совершает рейс из
Москвы в Хабаровск;

2 –
самолёт выполняет фигуру высшего пилотажа
“штопор,, вращаясь вокруг своей оси.

а); б)в первом;

в); г)во втором.

3. В каком случае тело можно считать
материальной точкой?

1 –
конькобежец проходит дистанцию
соревнований;

2 –
конькобежец-фигурист выполняет упражнения
произвольной программы.

а)во
втором; б);

в)в
первом; г).

4. В каком случае тело можно считать
материальной точкой?

1 –
за движением космического корабля следят
из центра управления на Земле;

2 –
за тем же кораблём наблюдает космонавт,
осуществляющий с ним стыковку в космосе.

а); б)во втором;

в); г)в первом.

5. Наблюдения над движениями футболиста
показали, что нападающий за время матча пробегает примерно12 км.
Как следует называть приведённую величину: перемещением или длиной пути ?

а)длиной пути; б);

в)перемещением; г).

6. Штурман, определяя утром положение корабля,
обнаружил, что корабль находится в точке, расположенной на100 кмк северу от пункта, в котором находился
корабль накануне вечером. Что выражает приведённое здесь число: перемещение или
пройденный путь ?

а); б)перемещение;

в); г)пройденный путь.

7. Дежурный по гаражу, принимая автомашину у
закончившего работу шофёра, записал увеличение показания счётчика на300 км. Что будет означать эта запись:
пройденный путь или перемещение ?

а); б)пройденный путь;

в); г)перемещение.

8. Можно ли принять за материальную точку
автомобиль, въезжающий в гараж ?

а)можно; б);

в)нельзя; г).

9. Вертолёт, пролетев в горизонтальном направлении по прямой40 км, повернул под углом90ºи пролетел
ещё30 км. Найти путь и перемещение вертолёта.

а)40 км,
30 км;

б)30 км,
50 км;

в)40 км,
50 км;

г)70 км,
50 км.

10. Мяч бросили
вертикально вверх от поверхности Земли. Достигнув высоты15 м,
он упал на Землю. Определите путь, пройденный мячом, и его перемещение.

а)путь
– 15 м, перемещение – 0;

б)путь
– 30 м, перемещение – 0;

в)путь
– 0 м, перемещение – 30;

г)путь
– 30 м, перемещение – 30.

11. Фигурист
движется по окружности радиусом20 м. За некоторое время он проехал расстояние, равное
половине длины окружности. Чему равны путь и перемещение фигуриста ?

а)путь
– 62,8 м, перемещение – 40 м;

б)путь
– 31,4 м, перемещение – 40 м;

в)путь
– 40 м, перемещение – 62,8 м;

г)путь
– 40 м, перемещение – 20 м.

12. Путь или
перемещение оплачивается при поездке в такси ?

а)перемещение; б);

Динамика и законы Ньютона

Динамика — это раздел механики, в котором законы движения тел устанавливаются через причины, обусловливающие его характер. Основу раздела составляют 3 закона Ньютона, являющиеся обобщением результатов наблюдений и специально поставленных экспериментов. Их не получится вывести из каких-либо более простых принципов.

Законы динамики имеют важное практическое значение. На них основаны расчёты, по которым сооружаются всевозможных машины и механизмы, инженерные конструкции, космические аппараты и прочая техника.. Однако стоит заметить, что утверждения Ньютона не являются универсальными даже в рамках классической механики и выполняются лишь в инерциальных системах отсчёта.

Однако стоит заметить, что утверждения Ньютона не являются универсальными даже в рамках классической механики и выполняются лишь в инерциальных системах отсчёта.

Три закона Ньютона:

1. Тело, находящееся в инерциальной системе отсчёта при условии отсутствия взаимодействия с другими объектами, будет находиться в покое или совершать прямолинейное и равномерное движение.
2. Сила, действующая на тело, полностью определяет скорость, с которой изменяется импульс этого тела.
3. Два тела действуют друг на друга с силами равными по модулю и направленными в противоположные стороны прямой, соединяющей эти тела.

Законы Ньютона нельзя изолировать друг от друга, так как они — система органичных и взаимосвязанных утверждений. Они применяются для решения любой задачи динамики, но второй закон принято считать основным, поскольку он непосредственно оперирует основными характеристиками движения.

В макроскопическом мире можно наблюдать большое количество всевозможных сил, которые являются проявлениями двух самых фундаментальных взаимодействий во вселенной — электромагнитного и гравитационного. Притяжение обусловлено гравитацией, а все остальные известные науке силы имеют электромагнитную природу.

Кратко ознакомившись с особенностями классической механики, можно понять, с какой целью используется понятие материальной точки. Нужно понимать, что физика не работают с реальными объектами, а лишь с абстрактными моделями. Это помогает облегчить теоретические построения и расчёты.

https://youtube.com/watch?v=Ko_o-T4QZ7s

Материальная точка

Материальная точка — это идеализированная концепция. Введение этого понятия абстрагирует от всех свойств тела, которые не имеют отношения к конкретному движению, например, его размер, форма, структура и т.д.

Каждая материальная точка, движущаяся в пространстве, описывается воображаемой линией, так называемой траекторией, которая может иметь множество форм.

Если траектория точки — прямая линия, то движение называется прямолинейным; если кривая линия, то движение называется криволинейным.

Как определить материальную току

Положение тела или материальной точки определяется только по отношению к другому материальному телу, которое обычно считается неподвижным и называется телом отсчета.

Произвольная система координат, связанная с этой системой отсчета, называется системой отсчета для положения материальной точки. Без выбора системы отсчета невозможно описать движение.

В случае прямолинейных движений, например, можно использовать систему координат, состоящую из прямой линии OS, вдоль которой происходит движение и которая начинается в точке O.

Кинетика Декарта

В более сложных случаях используется декартова прямоугольная система координат, в которой оси O и O перпендикулярны друг другу и пересекаются в точке O, которая является началом координат.

Длина части траектории, которую точка проходит от временного начала, называется длиной пути. Путь — это скалярная величина, характеризуемая только числовым значением s.

Если соединить начальное положение точки с ее конечным положением, то получится перемещение ∆ r точки за определенное время t .

Смещение точки является вектором, т.е. величиной, характеризующейся числовым значением и направлением. При линейном движении абсолютная величина вектора перемещения |∆ r | равна пути s.

Различают два основных и более простых вида движения твердого тела: поступательное и вращательное.

Движение тела, при котором линия, соединяющая две точки тела, перемещается параллельно самой себе по мере движения тела, называется поступательным движением.

Вращательное движение

Вращательное движение — это движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой (оси вращения).

В зависимости от характера связи пути со временем движение делится на равномерное и неравномерное.

Что мы узнали о материальной точке?

Что из нижеперечисленного является примером материальной точки?

Материальная точка, движение которой в пространстве не ограничено механическими ограничениями, называется свободной точкой.

Примерами свободных материальных точек являются искусственный спутник Земли, вращающийся вокруг Земли, и летящий аэроплан (если пренебречь их вращением).

Что такое материальная точка Малое тело?

Материальная точка — это стандартное понятие (абстракция) в классической механике, обозначающее тело с минимальными размерами, но с некоторой массой.

С одной стороны, материальная точка является самым простым объектом в механике, поскольку ее положение в пространстве определяется всего тремя числами.

Тело в механике классической физики

В механике классической физики, тело обычно рассматривается как материальная точка или система материальных точек, в зависимости от условий задачи и уровня точности, необходимого для получения нужных результатов.

Материальная точка — это абстрактная модель, в которой тело представляется как частица без размеров и формы, но обладающая массой и положением в пространстве. Она не имеет внутренней структуры и не подвержена взаимодействиям внутри себя. Примеры материальных точек — планеты, пули, молекулы газа и другие объекты, размеры которых можно пренебречь в сравнении с размерами их траектории или других интересующих нас характеристик.

Однако, не всегда тело может быть представлено в виде материальной точки. В некоторых случаях, размеры и формы объекта оказывают существенное влияние на его движение или взаимодействие с другими объектами. В таких случаях, система материальных точек может использоваться для аппроксимации и упрощения задачи. В системе материальных точек, тело представляется как совокупность точечных частиц, каждая из которых характеризуется своим положением и массой.

Таким образом, тело может быть рассмотрено как материальная точка в тех случаях, когда его размеры и форма не имеют существенного значения для решения поставленной задачи. В других случаях, внутренняя структура тела должна быть учтена, и тогда использование системы материальных точек позволяет упростить анализ и моделирование поведения объекта.

Упражнения

Упражнение №1

Можно ли считать автомобиль материальной точкой в следующих уловиях:а) при определении пути, который он прошел за $2 \space ч$, двигаясь со средней скоростью, равной $80 \frac{км}{ч}$;б) при обгоне им другого автомобиля?

Посмотреть ответ

Скрыть

Ответ:

В первом случае за указанное время автомобиль пройдет путь:$s = \upsilon_{ср} t$,$s = 80 \frac{км}{ч} \cdot 2 \space ч = 160 \space км$.

Очевидно, что такое расстояние намного больше размеров самого автомобиля. Поэтому в данном случае мы можем рассматривать его как материальную точку.

Во втором случае (когда автомобиль идет на обгон) мы не можем считать его материальной точкой. Ведь в этом случае для нас будут важны габариты автомобиля и движение отдельных его точек.

Упражнение №2

Самолет совершает перелет из Москвы во Владивосток. Может ли рассматривать самолет как материальную точку диспетчер, наблюдающий за его движением; пассажир этого самолета?

Посмотреть ответ

Скрыть

Ответ:

Диспетчер, являющийся телом отсчета, может рассматривать самолет как материальную точку, потому что размеры самолета намного меньше пролетаемого им расстояния.

А вот пассажир самолета не может принимать его за материальную точку, ведь он движется вместе с ним.

Упражнение №3

Когда говорят о скорости машины, поезда и других транспортных средств, тело отсчета обычно не указывают. Что подразумевают в этом случае под телом отсчета?

Посмотреть ответ

Скрыть

Ответ:

В случаях, когда речь идет о скоростях транспортных средств, под телом отсчета обычно подразумевают земную поверхность или любое тело, находящееся в состоянии покоя относительно Земли.

Упражнение №4

Мальчик стоял на земле и наблюдал, как его младшая сестра каталась на карусели. После катания девочка сказала брату, что и он сам, и дома, и деревья быстро проносились мимо нее. Мальчик же стал утверждать, что он вместе с домами и деревьями был неподвижен, а двигалась сестра. Относительно каких тел отсчета рассматривали движение девочка и мальчик? Объясните, кто прав в споре.

Посмотреть ответ

Скрыть

Ответ:

Наблюдающий за каруселью мальчик рассматривал движение карусели относительно поверхности Земли. Так, ни деревья, ни дома, ни сам мальчик не двигались относительно друг друга. Двигались только карусель и девочка на ней.

Девочка же рассматривала движение относительно своего сиденья карусели. Поэтому для нее в движении находились все остальные окружающие предметы (деревья, дома и др.)

Получается, что в этом споре правы оба. Просто брат с сестрой рассматривали движение относительно разных тел отсчета.

Упражнение №5

Относительно какого тела отсчета рассматривают движение, когда говорят: 

• скорость ветра равна $5 \frac{м}{с}$;
• бревно плывет по течению реки, поэтому его скорость равна нулю;
• скорость плывущего по реке дерева равна скорости течения воды в реке;
• любая точка колеса движущегося велосипеда описывает окружность;
• Солнце утром восходит на востоке, в течение дня движется по небу, а вечером заходит на западе?

Посмотреть ответ

Скрыть

Ответ:

• скорость ветра оценивают относительно поверхности Земли;
• плывущее бревно рассматривают относительно поверхности реки, которая сама находится в движении;
• дерево плывет со скоростью течения воды в реке, если рассматривать его движение относительно берега;
• точки колеса велосипеда движутся по окружности относительно самого велосипеда;
• движение Солнца по небу рассматривается относительно линии горизонта.

Физика 9 кл. Материальная точка. Система отсчёта

Подробности

Обновлено 18.06.2019 23:33

1. В чем состоит основная задача механики?
Основная задача механики состомт в определении положения тела в любой момент времени. 2. Что называется механическим движением?
Механическим движением тела называется изменение его положения в пространстве относительно других тел, происходящее с течением времени.

3. Что называется материальной точкой?

Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.

4. Обладает ли материальная точка массой? Имеет ли она размеры?
Да, материальная точка имеет массу тела и не имеет размеров.5. Материальная точка — это реальный объект или абстрактное понятие?
Материальных точек нет в природе.
Материальная точка — это абстрактное понятие,

6. С какой целью используется понятие «материальная точка»?

Использование понятия «материальная точка» позволяет упрощать решение задач и при этом получать точные результаты.

7. В каких случаях движущееся тело обычно рассматривают как материальную точку?

Тело можно считать материальной точкой только в тех случаях, когда его размерами (а значит, и формой, и вращением) можно пренебречь, поскольку они несущественны в условиях решаемой задачи.

8. При каком движении тела его можно рассматривать как материальную точку даже в том случае, если проходимые им расстояния сравнимы с его размерами?

Тело можно также принимать за материальную точку даже, если его размеры соизмеримы с проходимыми им расстояниям, но все точки этого тела должны двигаться одинаково.
Движение тела, при котором все его точки движутся одинаково, называется поступательным.

9. На каком примере можно показать, что одно и то же тело в одной ситуации можно считать материальной точкой, а в другой — нет?

Например:
За материальную точку можно принять самолет, если требуется определить среднюю скорость его движения на пути из Москвы в Новосибирск.
Но при вычислении силы сопротивления воздуха, действующей на летящий самолет, считать его материальной точкой нельзя, поскольку сила сопротивления зависит от размеров и формы самолета.

10. Какими величинами определяется положение тела (точки) в пространстве? Сколько таких величин?

Положение точки на линии, плоскости и в пространстве определяют соответственно одним, двумя или тремя числами координатами.

11. Что называется изменением координат тела?

Именение координат тела — это величина, равная разности конечного и начального значений координат (но не наоборот!).

12. В каком случае положение движущегося тела можно задать с помощью одной координатной оси?

При прямолинейном движении тела достаточно одной координатной оси для определения его положения.

13. Что такое тело отсчёта?
Телом отсчета называется тело, относительно которого рассматривается изменение положения других тел в пространстве.

14. Что называается системой отсчета?
Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

Физические основы механики

Физика — это наука о природе, изучающая наиболее простые и общие свойства, присущие материальному миру. Благодаря этому, она является универсальной базой для естествознания и техники, а также состоит из большого количества отдельных дисциплин — классической и квантовой механики, теории относительности, а также электродинамики, оптики и прочих.

Изучение физики начинается с механики — раздела, который рассматривает движение как изменение положения тела в пространстве с течением времени. Поэтому законы механики наиболее ясно выражают пространственно-временные отношения между объектами и событиями.

Основополагающие законы физики были в своё время установленны именно на основе наблюдения соответствующих явлений и экспериментов, из-за этого, за небольшим исключением, сфера их применения довольно ограничена. В частности, классическая механика распространяется лишь на медленное движение частиц и тел в макроскопических областях пространства. Перемещение на околосветовых скоростях подчиняется законам теории относительности, а свойствами микроскопических частиц занимается квантовая механика.

Классическая механика решает две основные задачи:

1. Установление законов движения — соотношений, позволяющих выяснить характер и показатели перемещения любого тела или системы в зависимости от его взаимодействия с другими объектами.
2. Нахождение таких общих соотношений между механическими характеристиками систем, не зависящими от их состава, строения и конкретного взаимодействия элементов.

Материальная точка

Вы увидите, что достаточно часто при расчетах мы можем пренебрегать деформированием тела. В таком случае говорят, что мы используем модель абсолютно твердого тела.

Вращательным движением мы тоже можем иногда пренебречь. Тогда остается рассматривать только поступательное движение тела. В этом случае мы используем модель материальной точки тела. То есть, мы рассматриваем движение только одной точки, подразумевая целое тело.

Что называется материальной точкой?

Соответственно, в определенных условиях мы можем пренебречь размерами и формой тела и рассматривать его как точку. Заметьте: в определенных условиях! Значит, все именно от них и зависит.

{"questions":,"answer":}}}]}

Давайте приведем пример, показывающий, что одно и то же тело в одной ситуации можно считать материальной точкой, а в другой — нет.

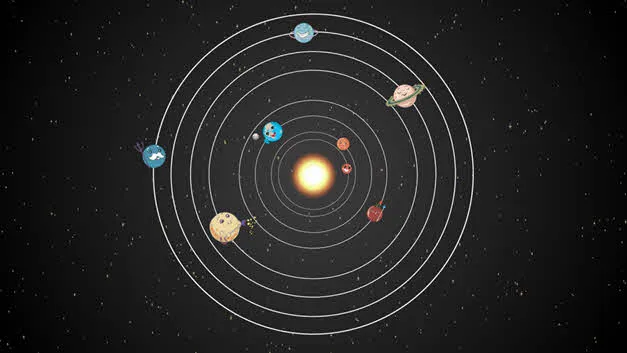
Так, если мы будем рассматривать движение планет вокруг Солнца, то мы можем их считать материальными точками (рисунок 5). В этом случае их размеры будут крайне малы в сравнении с расстояниями, которые они проходят.

Рисунок 5. Модель Солнечной системы

А вот если мы будем рассматривать вращение планеты вокруг своей оси, то понятие материальной точки использовать нельзя. Ведь здесь значение для нас будут иметь и размеры небесного тела и скорости движения разных его точек. Если мы захотим определить время восхода Солнца в разных местах на поверхности Земли, то столкнемся как раз с такой ситуацией (рисунок 6). В Приморском крае солнце взойдет на 7 часов раньше, чем в Московской области.

Рисунок 6. Схематическая карта часовых поясов

{"questions":,"answer":}}}]}

В каких случаях движущееся тело обычно рассматривают как материальную точку?

Чтобы мы могли использовать модель материальной точки, должно выполняться хотя бы одно из следующих условий:

• тело совершает поступательное движение;
• расстояние, проходимое телом, очень велико по сравнению с его размерами.

С какой целью используется понятие «материальная точка»?

Обратите внимание, что материальных точек в природе не существует, это всего лишь удобное понятие, которое упрощает решение многих задач и при этом позволяет получить достаточно точные результаты

{"questions":,"answer":}}}]}

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см

рисунок 8). Радиус-вектор, проведенный в точку A обозначим r, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

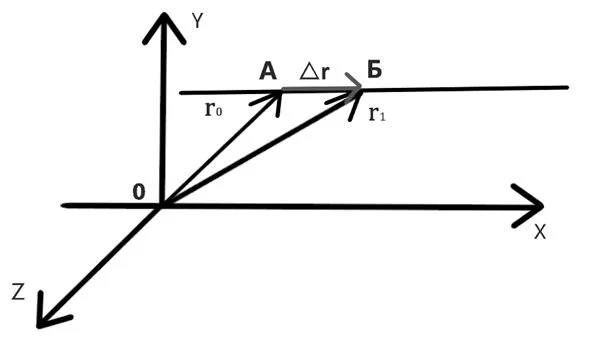
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r= r + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z– это компоненты изначальных векторов r и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;
r_y = r_0y + v_y*t;
r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х) и конечной (х₁) точки на ось ОХ.

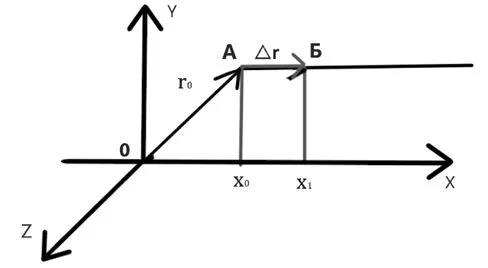Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x+ v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S + v*t.

Если точка начала двигаться из начала отсчета S = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x+ v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x- v*t = 0,03 — 5*t.

Система отсчета

Координатные оси

Чтобы определить положение тела в пространстве в какой-то момент его движения, мы используем координаты (рисунок 8).

Рисунок 8. Использование координат

В каком случае положение движущегося тела можно задать с помощью одной координатной оси?

Если рассматриваемое тело движется прямолинейно, то нам достаточно одной координатной оси для определения его положения.

Так, если мы возьмем тележку с капельницей и заставим ее двигаться по столу прямолинейно и поступательно, то ее положение в любой момент времени мы смоем определить с помощью линейки (рисунок 9).

Рисунок 9. Пример использования одной координатной оси для определения положения тела

В данном случае линейка расположена вдоль траектории движения тележки, которую мы принимаем за материальную точку. Линейка здесь — тело отсчета, а ее шкала — координатная ось. Положение тележки с капельницей будет определяться относительно нулевого деления линейки.

Так, велосипедиста, едущего равномерно по прямой дороге, мы тоже можем принять за материальную точку, а, например, дерево — за тело отсчета (рисунок 10). Положение велосипедиста мы можем определить, используя систему координат из всего одной координатной оси, связанной с деревом.

Рисунок 10. Пример использования одной координатной оси для определения положения тела

Может ли потребоваться больше координатных осей?

Вспомните движение мела по школьной доске. Это будет движением по плоскости. Здесь нам и потребуется вторая координатная ось (рисунок 11).

Рисунок 11. Пример использования двух координатных осей

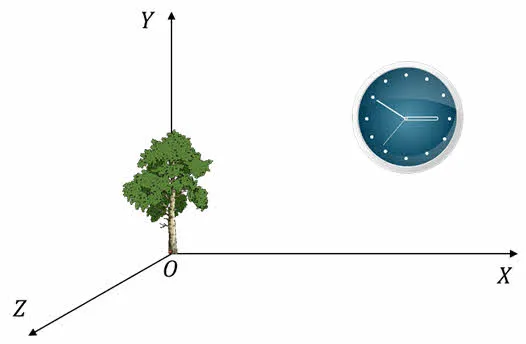
Три координатные оси нам понадобятся, если мы будет рассматривать движение тела в трехмерном пространстве. Например, движение вертолета (рисунок 12). Здесь мы будем использовать систему координат, связанную с телом отсчета и состоящую из трех взаимно перпендикулярных координатных осей.

Рисунок 12. Пример использования трех координатных осей

Прибор для определения времени

Во всех этих примерах, чтобы определить путь, который тело пройдет за определенное время, или его скорость, нам будет недостаточно координатной оси (или нескольких осей). Потребуется прибор для измерения времени — часы.

В случае с тележкой роль часов будет играть капельница. Из нее через равные промежутки времени падает капля. Поворачивая кран, мы можем настроить капельницу таким образом, чтобы капля падала раз в секунду. Потом мы можем посчитать количество промежутков между следами капель на столе и определить промежуток времени.

Выводы

Для определения положения движущегося тела в любой момент времени, вида движения, скорости тела и некоторых других характеристик движения необходимы тело отсчета, связанная с ним система координат (или одна координатная ось, если тело движется вдоль прямой) и прибор для измерения времени.

Так мы подошли к новому определению. Что такое система отсчета?

{"questions":,"answer":}}}]}