Как определить атомный радиус в таблице менделеева

Размеры и форма орбиталей

Более подробную информацию о строении атома, учитывающую двойственный характер природы электрона и принцип неопределенности, можно получит из решения уравнения Шредингера. Для одноэлектронных систем типа атома водорода оно может быть произведено аналитически без каких-либо вспомогательных приближений. При этом атом удобно рассматривать в сферических координатах, начало которых расположено в центре тяжести ядра. Тогда каждому электрону будет соответствовать радиус-вектор с координатами $r$ (расстояние между электроном и ядром), $\theta $ (угол наклона) и $\varphi $ (угол поворота), а решение уравнения Шредингера можно будет искать в виде произведения двух функций, одна из которых зависит только от $r$, а другая — от углов $\theta $ и $\varphi $.

$\Psi =R\left(r\right)\Theta \left(\theta ,\varphi \right)$ (7)

Не останавливаясь подробно на всех выкладках, отметим, что решение уравнения Шредингера в полярных координатах удовлетворит краевому условию $R(\infty) = 0$, если энергия электрона соответствует формуле (5)

Рассмотрим волновые функции $\Psi $, получающиеся при $n=1$ и $n=2$.

При $n=1$ и $l=0$ $\Theta $ становится постоянным числом, не зависящим ни от $r$, ни от $\theta $, ни от $\varphi $ и $\Psi = R$. При $n=1$ решение уравнения для R имеет вид:

$R=\frac{1}{\sqrt{\pi r^3_0}}e^{-\frac{r}{r_0}}$ (8)

где $r_0$ — первый боровский радиус.

Интересно установить, на каком расстоянии от ядра вероятность нахождения электрона максимальна. Ее можно найти как максимум выражения $R^24\pi r^2$.

Расчет показывает, что наибольшей вероятности нахождения электрона соответствует расстояние от ядра, равное первому боровскому радиусу $r_0$.

При $n=2$ и $l=0$

$\Psi =R=N_2\left(\frac{r}{r_0}-2\right)e^{-\frac{r}{2r_0}}$ (9)

где $N_2$ — нормировочный множитель, выбираемый таким образом, чтобы соблюдалось равенство

Значение $\Psi $ здесь также не зависит от углов наклона и поворота При этом наибольшей вероятности нахождения электрона соответствует второй боровский радиус.

Очевидно, собственные функции электронов с $l=0$ ($s$-электронов) не зависят от угловых координат, а зависят только от радиуса. Следовательно, $s$-орбитали обладают шаровой симметрией (рис.1).

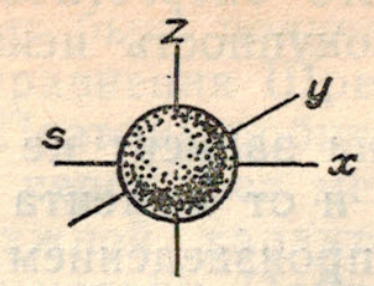Рисунок 1.

При $n=2$ и $l=1$

$R=N_3re^{-\frac{r}{2r_0}}$ (10)

а для $\Theta $ возможен набор значений:

Рисунок 2.

Эти значения соответствуют значениям магнитного квантового числа $m_l = 0$ и $m_l = ±1$.

Здесь мы видим, что значения $\Theta $ и $\Psi $ не зависят от угла поворота $\varphi $, (т.к. по абсолютному значению $e^\pm i \varphi = 1$) т.е. $p$-орбитали обладают радиально-осевой симметрией. Перейдя к декартовым координатам и рассматривая линейные комбинации решений с тремя различными значениями $\Theta $, можно прийти к выводу, что орбитали с $m_l = 0$, $m_l = 1$ и $m_l = -1$ симметричны относительно осей координат $x$, $y$ и $z$. Иначе говоря, их оси симметрии вращения взаимно перпендикулярны. Соответствующие р-орбиталям электронные облака имеют вид объемных «восьмерок» или гантелей, расположенных взаимно перпендикулярно (рис.):

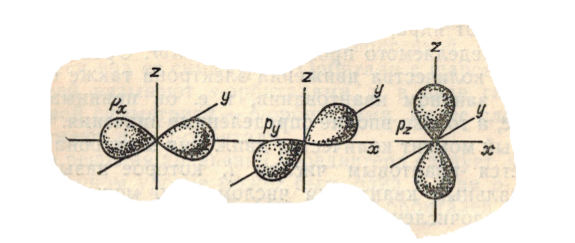Рисунок 3.

Граничные поверхности $d$- орбиталей имеют форму розетки или сложной гантели с тороидом (рис.4). Таких орбиталей $5$, и каждая соответствует какому либо значению $m_l$ от $-2$ до $+2$.

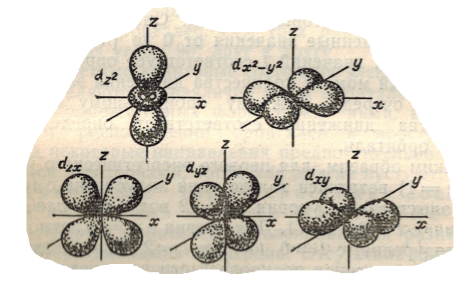Рисунок 4.

Симметрия и форма $f$-орбиталей сложны для наглядного изображения форму. При этом те и другие также отличаются друг от друга не только по форме, но и по взаимному расположению в пространстве, что соответствует различным значениям магнитного квантового числа $m_l$.

Вообще, симметрия орбитали или, в упрощенном понимании — ее геометрическая форма, является важной характеристикой орбитали, характеризующей способность взаимодействовать с орбиталями других атомов, близких по энергии и симметрии, с образованием химических связей

Метод рентгеноструктурного анализа

Для определения радиуса атома по методу рентгеноструктурного анализа необходимо провести рентгеноструктурное исследование кристалла и анализировать полученные данные. При этом используется так называемый метод наименьших квадратов, который позволяет получить наиболее точное приближение радиуса атома.

Определение радиуса атома методом рентгеноструктурного анализа имеет ряд преимуществ. Во-первых, этот метод позволяет анализировать как металлические, так и неметаллические материалы. Во-вторых, он обеспечивает высокую точность результатов и возможность получить пространственное представление о структуре атомов в веществе.

Таким образом, метод рентгеноструктурного анализа является важным инструментом в определении радиуса атома на основе данных из таблицы Менделеева. Он широко используется в различных областях науки и технологий, таких как материаловедение, физика, химия и биология.

Принцип работы метода

В таблице Менделеева радиус атомов представлен в пикометрах (pm) и может быть разным для различных элементов. Больший радиус атома обычно свидетельствует о более массивной структуре элемента, тогда как меньший радиус атома указывает на менее массивные атомы. Однако, для точного определения радиуса атома, необходимо учитывать другие факторы, такие как состояние атома (возбужденное или основное), углубление и источник данных.

Методы определения радиуса атома по таблице Менделеева могут также варьироваться в зависимости от конкретной задачи и требуемой точности. Один из таких методов — метод Коссель.

Преимущества и ограничения метода

Один из основных методов определения радиуса атома основан на данных, представленных в таблице Менделеева. Этот метод имеет ряд преимуществ и ограничений, которые надо учитывать при его применении.

Преимущества:

Простота применения

Для определения радиуса атома достаточно обратить внимание на его положение в таблице Менделеева и использовать значению, указанное в этой таблице.
Быстрота. Поскольку все необходимые данные указаны в таблице Менделеева, определение радиуса атома занимает минимальное время.
Частое обновление данных

Таблица Менделеева постоянно обновляется, и поэтому информация о радиусах атомов также обновляется. Это позволяет использовать этот метод для актуальных и достоверных результатов.

Ограничения:

Недостаточная точность. Метод определения радиуса атома по таблице Менделеева дает лишь приближенное значение, которое может отличаться от реального вида атома.
Зависимость от условий. Размер атома может варьировать в зависимости от условий эксперимента, таких как температура и давление. Поэтому, значения, полученные из таблицы Менделеева, могут не соответствовать реальным условиям.
Грубое приближение. Определение радиуса атома одним числом не учитывает его фактическую структуру и форму, что может привести к неточным результатам.

Все эти преимущества и ограничения следует учитывать при использовании метода определения радиуса атома по таблице Менделеева.

Как измеряется атомный радиус?

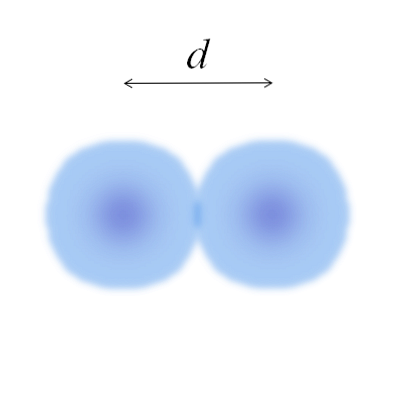
На основном изображении можно легко измерить диаметр ватных шариков, а затем разделить его на два. Однако сфера атома не полностью определена. Почему? Потому что электроны циркулируют и диффундируют в определенных областях пространства: орбитали.

Поэтому атом можно рассматривать как сферу с неощутимыми краями, о которых невозможно точно сказать, в какой степени они заканчиваются. Например, на верхнем изображении центральная область около ядра выглядит более интенсивной, а ее края размыты.

Изображение представляет двухатомную молекулу E₂ (как Cl₂, H₂, О₂, и т.д.). Предполагая, что атомы являются сферическими телами, если расстояние было определено d что разделяет оба ядра в ковалентной связи, то было бы достаточно разделить его на две половины (d/ 2) получить атомный радиус; точнее, ковалентный радиус E для E₂.

А если Е не образует с собой ковалентных связей, но это металлический элемент? то d это будет указано числом соседей, которые окружают Е в его металлической структуре; то есть по координационному числу (N.C) атома в упаковке (помните ватные шарики основного изображения).

Определение межъядерного расстояния

Определить d, это межъядерное расстояние для двух атомов в молекуле или упаковке, это требует методов физического анализа.

Одной из наиболее часто используемых является дифракция рентгеновских лучей, в которой пучок света облучается через кристалл, и изучается дифракционная картина, возникающая в результате взаимодействия электронов с электромагнитным излучением. В зависимости от упаковки могут быть получены различные дифракционные картины и, следовательно, другие значения d.

Если атомы «плотно» в кристаллической решетке, они будут представлять разные значения d по сравнению с тем, что они имели бы, если бы они были «удобными». Кроме того, эти межъядерные расстояния могут колебаться в значениях, поэтому атомный радиус фактически состоит из среднего значения таких измерений.

Как связаны атомный радиус и координационное число? В. Гольдшмидт установил взаимосвязь между ними, в которой для N.C. из 12 относительное значение равно 1; от 0,97 для упаковки, где атом имеет N.C, равный 8; 0,96 для N.C, равного 6; и 0,88 для N.C. из 4.

единицы

Из значений для N.C, равных 12, было построено много таблиц, сравнивающих атомные радиусы всех элементов периодической таблицы..

Поскольку не все элементы образуют такие компактные структуры (N.C меньше 12), соотношение В. Гольдшмидта используется для расчета их атомных радиусов и выражения для одной и той же упаковки. Таким образом, измерения атомных радиусов стандартизированы.

Но в каких единицах они выражают себя? при условии d имеет очень малую величину, следует прибегнуть к единицам ангстрем Å (10 ∙ 10-10м) или также широко используемый, пикометр (10 ∙ 10-12м).

Влияние радиусов атомов на физические свойства соединений

Радиусы атомов оказывают существенное влияние на физические свойства химических соединений. Размеры атомов влияют на их взаимодействие, образование кристаллической структуры и физические свойства материалов.

Одним из основных физических свойств, зависящих от радиуса атомов, является плотность. Чем больше радиус атома, тем меньше плотность соединения. Это связано с тем, что большие атомы занимают больше объема, поэтому для образования определенного количества соединения требуется больше массы.

Радиусы атомов также влияют на точку плавления и кипения соединений. Большие атомы имеют более слабые межатомные связи, что делает их более склонными к изменению фазы. Это объясняет, почему соединения с большими атомами часто имеют более низкие точки плавления и кипения.

Влияние радиусов атомов на физические свойства соединений также проявляется в их электропроводности. Маленькие атомы обычно обладают более высокой электропроводностью из-за более тесной упаковки и более сильных межатомных связей. Большие атомы имеют более слабые связи и хуже проводят электрический ток.

Кроме того, радиусы атомов могут влиять на магнитные свойства соединений. Некоторые соединения, содержащие металлы с большими атомами, могут обладать ферромагнитными свойствами из-за особенностей их электронной структуры.

В целом, радиусы атомов играют ключевую роль в определении физических свойств химических соединений. Понимание связи между радиусами атомов и физическими свойствами позволяет улучшить процессы синтеза, структурное проектирование и выбор материалов для конкретных целей.

Периодический закон

К середине XIX века учёные располагали множеством сведений о физических и химических свойствах разных элементов и их соединений. Появилась необходимость упорядочить эти знания и представить их в наглядном виде. Исследователи из разных стран пытались создать классификацию, объединяя элементы по сходству состава и свойств веществ, которые они образуют. Однако ни одна из предложенных систем не охватывала все известные элементы.

Пытался решить эту задачу и молодой русский профессор Д.И. Менделеев. Он собирал и классифицировал информацию о свойствах элементов и их соединений, а затем уточнял её в ходе многочисленных экспериментов. Собрав данные, Дмитрий Иванович записал сведения о каждом элементе на карточки, раскладывал их на столе и многократно перемещал, пытаясь выстроить логическую систему. Долгие научные изыскания привели его к выводу, что свойства элементов и их соединений изменяются с возрастанием атомной массы, однако не монотонно, а периодически.

Так был открыт периодический закон, который учёный сформулировал следующим образом: «Свойства элементов, а потому и свойства образуемых ими простых и сложных тел, стоят в периодической зависимости от их атомного веса».

Своё открытие Менделеев совершил почти за 30 лет до того, как учёным удалось понять структуру атома. Открытия в области атомной физики позволили установить, что свойства элементов определяются не атомной массой, а зависят от количества электронов, содержащихся в нём. Поэтому современная формулировка закона звучит так:

Свойства химических элементов, а также формы и свойства образуемых ими веществ и соединений находятся в периодической зависимости от величины зарядов ядер их атомов.

Этот принцип Менделеев проиллюстрировал в таблице, в которой были представлены все 63 известных на тот момент химических элемента. При её создании учёный предпринял ряд весьма смелых шагов.

<<Форма демодоступа>>

Во-первых, многочисленные эксперименты позволили Менделееву сделать вывод, что атомные массы некоторых элементов ранее были вычислены неправильно, и он изменил их в соответствии со своей системой.

Во-вторых, в таблице были оставлены места для новых элементов, открытие которых учёный предсказал, подробно описав их свойства.

Мировое научное сообщество поначалу скептически отнеслось к открытию русского химика. Однако вскоре были открыты предсказанные им химические элементы: галлий, скандий и германий. Это разрушило сомнения в правильности системы Менделеева, которая навсегда изменила науку. Там, где раньше учёному требовалось провести ряд сложнейших (и даже не всегда возможных в реальности) опытов — теперь стало достаточно одного взгляда в таблицу.

Теперь расскажем, как устроена Периодическая таблица элементов Менделеева и как ею пользоваться.

<<Форма семейного образования>>

История разработки таблицы Менделеева

Процесс разработки таблицы Менделеева был результатом долгого исследования различных свойств и характеристик элементов. Ученые уже давно пытались найти закономерности в свойствах элементов, но Менделееву удалось создать упорядоченную таблицу, в которой элементы располагались по возрастанию их атомных масс.

Одним из ключевых моментов, приведших к разработке таблицы Менделеева, было открытие новых элементов и определение их химических свойств. Ученые собирали информацию о различных элементах и их свойствах, пытаясь найти закономерности и систематизировать полученные данные.

В 1869 году Менделеев представил свою таблицу, в которой элементы располагались в порядке возрастания атомных масс, а также группировались по сходству химических свойств. Каждый элемент имел свое место в таблице, а его свойства можно было предсказать на основе расположения в таблице.

Разработка таблицы Менделеева оказала огромное влияние на развитие химии и других наук. Она помогла ученым лучше понять структуру и свойства элементов, а также предсказывать их химическое поведение. С тех пор таблица Менделеева подвергалась ряду изменений и дополнений, но ее основные принципы остались неизменными.

Сегодня таблица Менделеева является неотъемлемой частью обучения химии и используется во множестве научных и практических задач. Ее разработка стала важным вехой в истории химии и оказала огромное влияние на развитие этой науки.

Первый постулат Бора и размер атома водорода

Ранее (см. «Атомные орбитали») уже говорилось, что в свое время, пытаясь усовершенствовать планетарную модель атома, чтобы объяснить линейчатый характер спектров простых веществ, в частности — водорода, Н.Бор постулировал, что энергия электронов в атоме квантуется, т.е. изменяется скачкообразно. При этом каждому энергетическому уровню соответствует круговая орбита, по которой электрон вращается вокруг ядра. В классической механике вращательного движения существует понятие момента импульса $mvr$ (где $m$ — масса объекта, $v$ — скорость его движения, $r$ — радиус кривизны его траектории, который является постоянным в случае движения по поверхности сферы). По теории Бора, момент импульса электрона равен целому числу $n$ (это уже известное нам главное квантовое число) квантов энергии $\frac{h}{2\pi }$, где $h$ — постоянная Планка. Математическим выражением этого постулата является равенство:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

$mvr=n\frac{h}{2\pi }$ (1)

из которого следует, что момент импульса тоже квантуется. С точки зрения теории Бора это связано с тем, что каждому энергетическому уровню соответствует определенный радиус орбиты, по которой электроны, обладающие энергией этого уровня, вращаются вокруг ядра.

Кроме радиуса, неизвестным в нашем уравнении является скорость. Ее можно найти из условия равенства центробежной и центростремительной сил в системе ядро-электрон. Центробежная сила равна $\frac{mv^2}{r}$. Центростремительная сила определяется взаимодействием ядра и электрона как двух одинаковых разноименных зарядов по закону Кулона и составляет $\frac{e^2}{r^2}$, где е — заряд электрона и протона, которые у них одинаковы по абсолютной величине. При условии равенства центробежной и центростремительной сил у атома водорода в основном состоянии:

$\frac{mv^2}{r}=\frac{e^2}{r^2}$ (2)

Решая систему уравнений (1) и (2) относительно $r$ и $v$, найдем, что

$r=\frac{h^2}{4{\pi }^2me^2}n^2$ (3)

$v=\frac{2\pi e^2}{nh}$ (4)

Подставляя в уравнение (3) $h = 6,63\times 10-34 Дж^*с$, $m = 9,11\times 10-31 кг$, $e = 1,602\times 10-19 Кл$ и $n=1$, получим $r = 0,053 нм$. Эта величина называется первым боровским радиусом и соответствует «границе» атома водорода в основном состоянии. Очевидно, второй, третий и т.д. боровские радиусы будут в $n^2$ раз больше первого.

Для дальнейших рассуждений представляет интерес формула кинетической энергии электрона. Подставляя выражение для скорости (4) в формулу кинетической энергии, получаем

$E=\frac{mv^2}{2}=-\frac{2{\pi }^2me^4}{h^2n^2}$ (5)

В случае водородоподобного иона, в котором электрон движется вокруг ядра, обладающего произвольным зарядом $Z$, кратным по абсолютной величине и противоположным по знаку заряду электрона, энергия возрастает в $Z^2$ раз и ее выражение принимает вид:

$E=-\left(2{\pi }^2mZ^2e^4\right)\left(h^2n^2\right)$ (6)

Очевидно, что кинетическая энергия электрона убывает обратно пропорционально $n^2$.

Как определить радиус атома по таблице Менделеева

Шаг 1: Выбор элемента

Для определения радиуса атома необходимо выбрать интересующий нас химический элемент. Элементы в таблице Менделеева расположены по возрастанию атомного номера, поэтому для поиска нужного элемента можно использовать номер элемента или его символ.

Шаг 2: Поиск данных

После выбора элемента необходимо найти его данные в таблице Менделеева. В таблице указаны атомный номер, символ элемента, атомная масса и электронная конфигурация. Для определения радиуса атома наиболее важными являются атомный номер и электронная конфигурация.

Атомный номер показывает количество протонов в ядре атома и также равен количеству электронов в атоме. Электронная конфигурация представляет собой информацию о распределении электронов по энергетическим уровням и подуровням.

Шаг 3: Расчет радиуса атома

На основе атомного номера и электронной конфигурации можно определить радиус атома. Обычно используется эффективный радиус, который представляет собой расстояние от ядра до наиболее дальнего электрона.

Расчет радиуса атома может проводиться с использованием эмпирических формул и экспериментальных данных. Одной из распространенных формул для расчета радиуса атома является формула Клеппера-Петерсона.

Пример

Давайте рассмотрим пример для определения радиуса атома кислорода (O). Из таблицы Менделеева мы узнаем, что атомный номер кислорода равен 8, а его электронная конфигурация состоит из 2 электронов в первом энергетическом уровне и 6 электронов во втором энергетическом уровне.

С использованием эффективного радиуса можно рассчитать, что радиус атома кислорода составляет примерно 66 пикометров (1 пикометр = 1 × 10^-12 метра).

Таким образом, определение радиуса атома по таблице Менделеева является важным шагом в изучении свойств и характеристик элементов.

Элемент	Атомный номер	Эффективный радиус (пикометры)
Водород (H)	1	25
Гелий (He)	2	31
Кислород (O)	8	66
Углерод (C)	6	67

Откуда взялись атомы?

Как известно, сейчас различные атомы сгруппированы в таблицу Менделеева. В ней насчитывается 118 (а если с предсказанными, но еще не открытыми элементами — 126) элементов, не считая изотопов. Но так было далеко не всегда.

В самом начале формирования Вселенной никаких атомов не было и подавно, существовали лишь элементарные частицы, под воздействием огромных температур взаимодействующие между собой. Как сказал бы поэт, это был настоящий апофеоз частиц. В первые три минуты существования Вселенной, из-за понижения температуры и совпадения еще целой кучи факторов, запустился процесс первичного нуклеосинтеза, когда из элементарных частиц появились первые элементы: водород, гелий, литий и дейтерий (тяжелый водород). Именно из этих элементов образовались первые звезды, в недрах которых проходили термоядерные реакции, в результате которых водород и гелий «сгорали», образуя более тяжелые элементы. Если звезда была достаточно большой, то свою жизнь она заканчивала так называемым взрывом «сверхновой», в результате которого атомы выбрасывались в окружающее пространство. Так и получилась вся таблица Менделеева.

Вселенная

Методы измерения радиуса атома

Существует несколько методов, которые позволяют определить радиус атома:

Рентгеноструктурный анализ – метод, основанный на использовании рентгеновского излучения. Путем анализа рассеянного рентгеновского излучения от атомов в кристаллической решетке можно определить расстояния между атомами и тем самым получить информацию о размере атомов.
Метод дифракции электронов – используется для измерения радиуса атома в конкретном соединении. Электроны, испущенные с помощью электронного микроскопа, проходят через образец и дифрагируют на решетке. Анализ дифракционной картины позволяет определить расстояние между атомами и, соответственно, их радиусы.
Метод рентгеновской флуоресценции – основан на явлении излучения атомом рентгеновских лучей после поглощения рентгеновского излучения. Замеряя энергию флуоресцентного излучения и применяя физические модели, можно определить размеры атомов.
Методы, основанные на спектральных характеристиках – измеряются энергия или длина волн излучения, поглощенного или испущенного атомами вещества. Путем сравнения данных с эталонными значениями и использования теоретических моделей можно определить радиус атомов.
Методы, основанные на электронных и магнитных свойствах – используются для измерения размеров атомов в молекулах. Например, метод электронного парамагнитного резонанса позволяет измерить расстояние между атомами по изменению парамагнитного сигнала.

Выбор метода зависит от типа вещества, его состояния и требуемой точности измерения радиуса атома.

Структура Периодической системы элементов

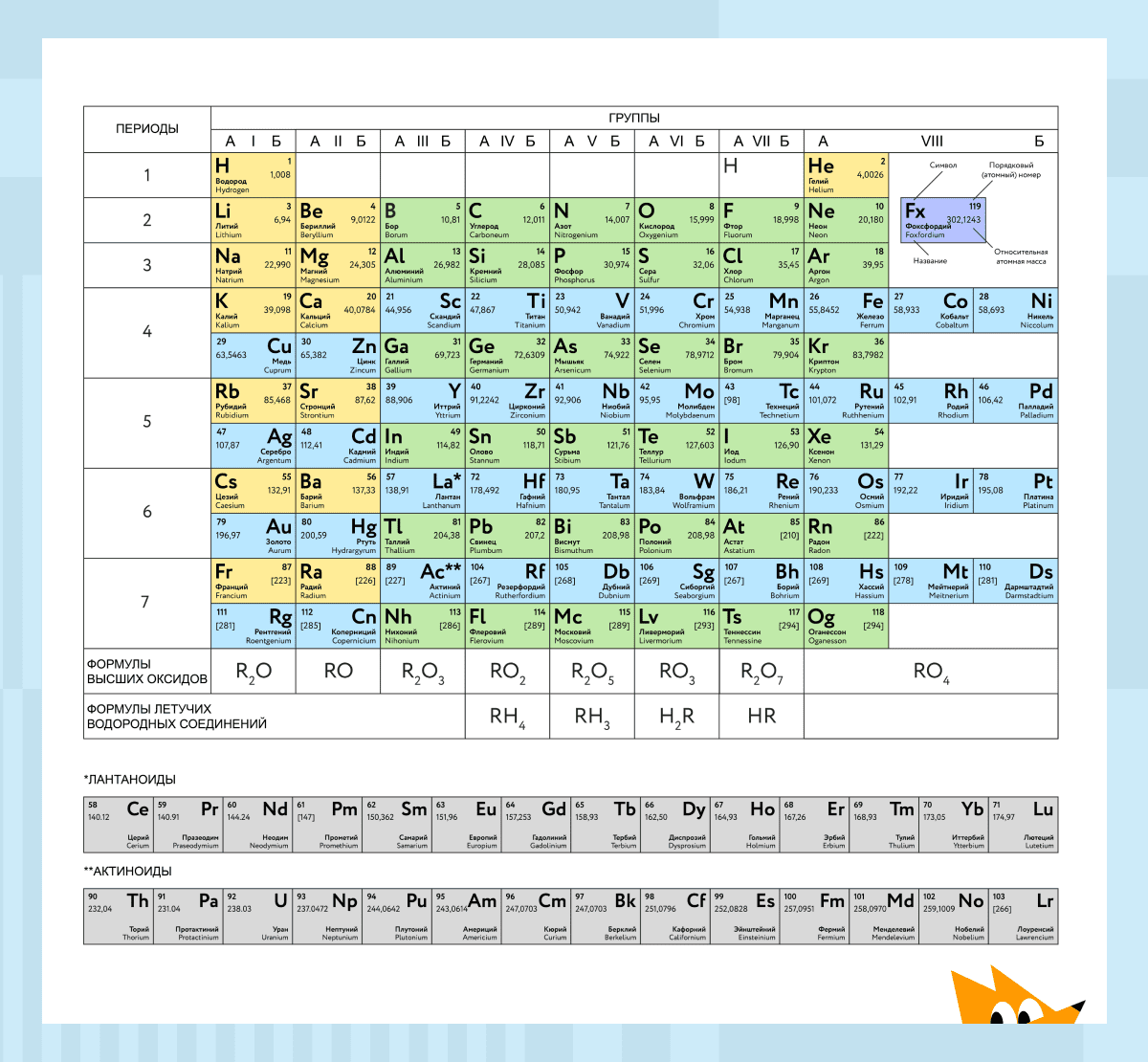
На настоящий момент Периодическая таблица Менделеева содержит 118 химических элементов. Каждый из них занимает своё место в зависимости от атомного числа. Оно показывает, сколько протонов содержит ядро атома элемента и сколько электронов в атоме находятся вокруг него. Атом каждого последующего элемента содержит на один протон больше, чем предыдущий.

Периоды — это строки таблицы. На данный момент их семь. У всех элементов одного периода одинаковое количество заполненных электронами энергетических уровней.

Группы — это столбцы. В группы в Периодической таблице объединяются элементы с одинаковым числом электронов на внешнем энергетическом уровне их атомов. В кратком варианте таблицы, используемой в школьных учебниках, элементы разделены на восемь групп. Каждая из них делится на главную (A) и побочную (B) подгруппы, которые объединяют элементы со сходными химическими свойствами.

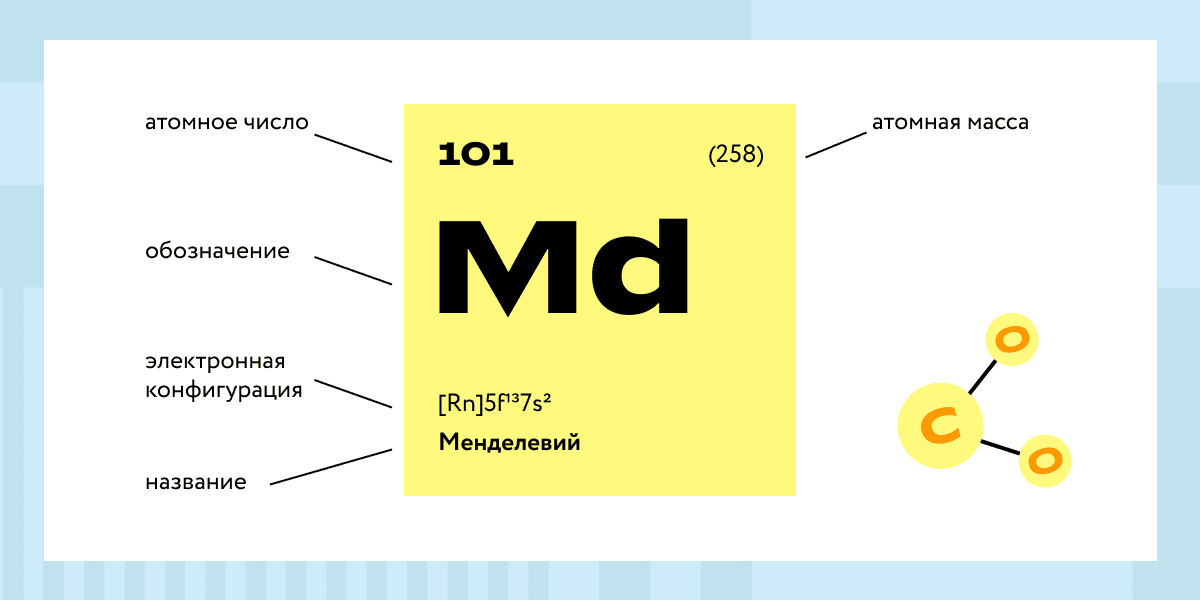
Каждый элемент обозначается одной или двумя латинскими буквами. Порядковый номер элемента (число протонов в его ядре) обычно пишется в левом верхнем углу. Также в ячейке элемента указана его относительная атомная масса (сумма масс протонов и нейтронов). Это усреднённая величина, для расчёта которой используются атомные массы всех изотопов элемента с учётом их содержания в природе. Поэтому обычно она является дробным числом.

Чтобы узнать количество нейтронов в ядре элемента, необходимо вычесть его порядковый номер из относительной атомной массы (массового числа).

Атомный радиус в химии и кристаллографии

Какие бывают виды

Данная характеристика сильно варьируется, в зависимости от того, в какой химической связи состоит атом. Поскольку все вещества в природе в подавляющем своем большинстве состоят из молекул, понятие а. р. используют для определения межатомных расстояний в молекуле. А данная характеристика зависит от свойств входящих в молекулу атомов, т. е. их положения в Периодической системе химических элементов. Обладая разными физическими и химическими свойствами, молекулы образуют все огромное разнообразие веществ.

По сути, эта величина очерчивает сферу действия силы электрического притяжения ядра атома и его внешних электронных оболочек. За пределами этой сферы в действие вступает сила электрического притяжения соседнего атома. Существует несколько типов химической связи атомов в молекуле:

ковалентная;
ионная;
металлическая;
ван-дер-ваальсова.

Соответственно этим связям таким же будет и атомный радиус.

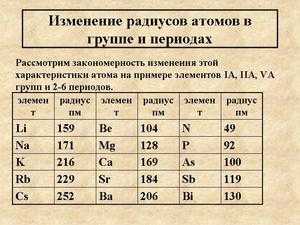
Как зависит от типа химической связи

При ковалентной связи АР определяется как половина расстояния между соседними атомами в одинарной химической связи Х—Х, причем Х — это неметалл, ибо данная связь свойственна неметаллам. Например, для галогенов ковалентный радиус будет равен половине межъядерного расстояния Х—Х в молекуле Х2, для молекул селена Se и серы S — половине расстояния Х—Х в молекуле Х8, для углерода С он будет равен половине кратчайшего расстояния С—С в кристалле алмаза.

Данная химическая связь обладает свойством аддитивности, т. е. суммирования, что позволяет определять межъядерные расстояния в многоатомных молекулах. Если связь в молекуле двойная или тройная, то ковалентный АР уменьшается, т. к. длины кратных связей меньше одинарных.

При ионной связи, образующейся в ионных кристаллах, используют значения ионного АР для определения расстояния между ближайшими анионом и катионом, находящимися в узлах кристаллической решетки. Такое расстояние определяется как сумма радиусов этих ионов.

Существует несколько способов определения ионных радиусов, при которых отличаются значения у индивидуальных ионов. Но в результате эти способы дают примерно одинаковые значения межъядерных расстояний. Эти способы или системы были названы в честь ученых, проводивших в этой области соответствующие исследования:

Гольдшмидта;
Полинга;
Белова и Бокия;
других ученых.

При металлической связи, возникающей в кристаллах металлов, АР принимаются равными половине кратчайшего расстояния между ними. Металлический радиус зависит от координационного числа К. При К=12 его значение условно принимается за единицу. Для координационных чисел 4, 6 и 8 металлические радиусы одного и того же элемента соответственно будут равны 0.88, 0.96 и 0.98.

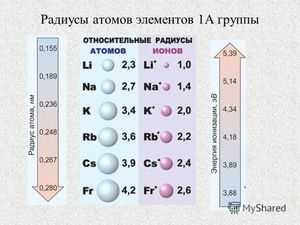
Если взять два разных металла и сравнить металлические радиусы их элементов, то близость этих значений друг к другу будет означать необходимое, но недостаточное условие взаимной растворимости этих металлов по типу замещения. Например, жидкие калий К и литий Li в обычных условиях не смешиваются и образуют два жидких слоя, потому что их металлические радиусы сильно различаются (0.236 нм и 0.155 нм соответственно), а калий К с цезием Cs образуют твердый раствор благодаря близости их радиусов (0.236 нм и 0.268 нм).

Ван-дер-ваальсовы АР используют для определения эффективных размеров атомов благородных газов, а также расстояний между ближайшими одноименными атомами, принадлежащими разным молекулам и не связанными химической связью (пример — молекулярные кристаллы). Если такие атомы сблизятся на расстояние, меньшее суммы их ван-дер-ваальсовых радиусов, между ними возникнет сильное межатомное отталкивание. Эти радиусы определяют минимально допустимые границы контакта двух атомов, принадлежащих соседним молекулам.

Кроме того, данные АР используют для определения формы молекул, их конформаций и упаковки в молекулярных кристаллах. Известен принцип «плотной упаковки», когда молекулы, образующие кристалл, входят друг в друга своими «выступами» и «впадинами». На основе этого принципа интерпретируются данные кристаллографии и предсказываются структуры молекулярных кристаллов.