Алгебра логики джорджа буля

Способы представления булевой функции

С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:

• Совершенная дизъюнктивная нормальная форма (СДНФ)
• Совершенная конъюнктивная нормальная форма (СКНФ)
• Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Совершенная дизъюнктивная нормальная форма (ДНФ)

Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.

Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.

Совершенная конъюнктивная нормальная форма (КНФ)

Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.

Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.

Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1

Алгоритм построения СДНФ для булевой функции

1. Построить таблицу истинности для функции
2. Найти все наборы аргументов, на которых функция принимает значение 1
3. Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
4. Объединить все простые конъюнкции с помощью дизъюнкции

Алгоритм построения СКНФ для булевой функции

1. Построить таблицу истинности для функции
2. Найти все наборы аргументов, на которых функция принимает значение 0
3. Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
4. Объединить все простые дизъюнкции с помощью конъюнкции

Алгоритм построения полинома Жегалкина булевой функции

Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.

1. Построить таблицу истинности для функции
2. Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
3. Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
4. Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
5. Выписать булевы наборы, на которых значение последнего столбца равно единице
6. Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.

3 Двойственные функции

Определение 4 (Двойственная функция). Функция g ( x 1 . x n ) = ¬f ( ¬x 1 . ¬x n ) называется двойственной функцией к функции f и обозначается f * .

Пример 2 (двойственные функции).

( x & y ) * = ¬ ( ¬x & ¬y ) = x Ъ y .

Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f * ( x 1 . x n ) * = ( ¬f ( ¬x 1 . ¬x n )) * = * = ¬¬f ( ¬¬x 1 . ¬¬x n ) = * = f ( x 1 . x n ) *

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора ( x 1 . x n ) на ( ¬x 1 . ¬x n ) соответствует «переворачиванию» таблицы. Действительно, наборы ( x 1 . x n ) и ( ¬x 1 . ¬x n ) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & y и x Ъ y , задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x Е y и x є y , задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее: f 0 ( f 1 . f m ) * = f 0 * ( f 1 * . f m * )

Доказательство. f 0 ( f 1 ( x 1 . x n ) . f m ( x 1 . x n )) * =

= ¬f 0 ( f 1 ( ¬x 1 . ¬x n ) . f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬¬f 1 ( ¬x 1 . ¬x n ) . ¬¬f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬f 1 * ( x 1 . x n ) . ¬f m * ( x 1 . x n )) =	*
= f 0 * ( f 1 * ( x 1 . x n ) . f m * ( x 1 . x n ))	*

Примеры схемной реализации логических элементов

Диодно-транзисторная логика (ДТЛ)

ДТЛ. Схема, реализующая логическую функцию 2И-НЕ

Приведём пример построения логического элемента на базе диодно-транзисторной схемы, составленной из входной линейки диодов VD1, VD2, на катоды которых приходят сигналы либо высокого уровня (логическая «1»), либо низкого уровня (логический «0»), и транзисторного ключа.

Если хотя бы на один из входов Inp1, Inp2 или на оба сразу приходит логический «0», то на базу транзистора подается низкий уровень. Транзистор закрыт. На выходе Out появляется высокий уровень, то есть логическая «1».

Если на оба входа Inp1, Inp2 подаются сигналы высокого уровня, транзистор открыт и на выходе Out появляется низкий уровень, то есть логический «0». Таким образом мы видим, что схема реализует логическую функцию «И-НЕ». На практике, если входных сигналов несколько, к названию функции добавляется количество входов. Соответственно, этот логический элемент носит название 2И-НЕ.

Транзисторно-транзисторная логика (ТТЛ)

ТТЛ. Схема, реализующая логическую функцию 2И-НЕ

Схема ТТЛ выполнена в варианте интегральной микросхемы и реализует ту же функцию 2И-НЕ, только в качестве входного элемента работает многоэмиттерный транзистор, объединяющий функции входных диодов и повторителя сигнала.

При подаче на любой из эмиттеров или на оба эмиттера транзистора VT1 сигналов низкого уровня (логический «0») транзистор VT1 открывается, на его коллекторе и, соответственно, на базе VT2 появляется низкий уровень. Транзисторный ключ VT2 инвертирует сигнал, на его выходе появляется высокий уровень (логическая «1»).

При подаче на оба эмиттера VT1 сигналов высокого уровня (логическая «1») картина обратная, то есть транзистор VT1 закрыт, высокий потенциал на его выходе открывает транзистор VT2, на выходе которого появляется низкий уровень (логический «0»).

Определение и примеры

Существует 16 различных логических функций с двумя переменными:

1. Логическое И (AND): возвращает 1 только если оба аргумента равны 1, иначе возвращает 0. Пример: 1 AND 1 = 1, 1 AND 0 = 0.
2. Логическое ИЛИ (OR): возвращает 1 если хотя бы один из аргументов равен 1, иначе возвращает 0. Пример: 1 OR 0 = 1, 0 OR 0 = 0.
3. Логическое НЕ (NOT): возвращает противоположное значение аргумента. Пример: NOT 1 = 0, NOT 0 = 1.
4. Исключающее ИЛИ (XOR): возвращает 1, если только один из аргументов равен 1, иначе возвращает 0. Пример: 1 XOR 0 = 1, 1 XOR 1 = 0.
5. Импликация (IMPL): возвращает 1, если первый аргумент равен 0 или оба аргумента равны 1. Возвращает 0, если только первый аргумент равен 1 и второй аргумент равен 0. Пример: 0 IMPL 1 = 1, 1 IMPL 0 = 0.
6. Равносильность (EQV): возвращает 1, если оба аргумента равны 1 или оба аргумента равны 0. Возвращает 0, если только один из аргументов равен 1. Пример: 0 EQV 0 = 1, 0 EQV 1 = 0.
7. Штрих Шеффера (NAND): возвращает 0, если оба аргумента равны 1, и возвращает 1 в остальных случаях. Пример: 1 NAND 0 = 1, 0 NAND 0 = 1.
8. Стрелка Пирса (NOR): возвращает 1, если оба аргумента равны 0, и возвращает 0 в остальных случаях. Пример: 0 NOR 1 = 0, 1 NOR 1 = 0.
9. Отрицание первого аргумента (NXOR): возвращает 1, если оба аргумента равны 0 или оба аргумента равны 1. Возвращает 0, если первый аргумент равен 1 и второй аргумент равен 0. Пример: 0 NXOR 0 = 1, 1 NXOR 0 = 0.
10. Конъюнкция (ANDO): возвращает 1, если оба аргумента равны 1, и возвращает 0 в остальных случаях. Пример: 1 ANDO 0 = 0, 1 ANDO 1 = 1.
11. Дизъюнкция (ORO): возвращает 0, если оба аргумента равны 0, и возвращает 1 в остальных случаях. Пример: 1 ORO 0 = 1, 0 ORO 0 = 0.
12. Импликация без связки (IMPLB): возвращает 1, если хотя бы один из аргументов равен 0, и возвращает 0 только если оба аргумента равны 1. Пример: 0 IMPLB 1 = 1, 1 IMPLB 1 = 0.
13. Инверсия второго аргумента (NOTB): возвращает противоположное значение второго аргумента. Пример: NOTB 1 = 0, NOTB 0 = 1.
14. Собственная импликация (IMPLS): возвращает 1, если только один из аргументов равен 0, и возвращает 0 в остальных случаях. Пример: 0 IMPLS 1 = 0, 1 IMPLS 0 = 0.
15. Не равно (NEQ): возвращает 0, если оба аргумента равны 1 или оба аргумента равны 0. Возвращает 1, если только один из аргументов равен 1. Пример: 0 NEQ 0 = 0, 0 NEQ 1 = 1.
16. Сложение по модулю 2 (SUM2): возвращает результат сложения двух аргументов по модулю 2. Пример: 0 SUM2 1 = 1, 1 SUM2 1 = 0.

Эти функции являются базисными для построения более сложных логических функций и широко применяются в электронике, компьютерных науках и информатике.

AND-функция в логике

AND-функция может быть представлена в виде таблицы истинности, которая показывает значения функции для всех возможных комбинаций входных аргументов:

Аргумент 1	Аргумент 2	AND
1
1
1	1	1

В логических выражениях AND-функцию обозначают символом ∙ или *, например: A ∙ B или A * B.

AND-функция является базовой для построения более сложных логических выражений. Она используется во многих областях, включая программирование, электронику и компьютерные науки.

OR-функция в логике

OR-функция имеет следующую таблицу истинности:

• OR(ложь, ложь) = ложь
• OR(ложь, истина) = истина
• OR(истина, ложь) = истина
• OR(истина, истина) = истина

Значение OR-функции зависит только от значений входных переменных и не зависит от их порядка или количества.

OR-функция может быть представлена в виде логического выражения с использованием символа «∨» или «+».

Например, OR-функция для двух переменных может быть записана следующим образом:

F = A ∨ B

Где A и B — входные переменные, а F — выходное значение OR-функции.

OR-функция широко применяется в различных областях, включая электротехнику, информатику и математику. Она используется для объединения условий и выполнения действий, если хотя бы одно условие истинно.

Двойственные функции

Функции тождественны, если $f(x_1, x_2, \dots, x_n)=g(x_1, x_2, \dots, x_n)$ на всех наборах
аргументов (таблицы истинности совпадают).

$f(\overline{x_1},\overline{x_2},\dots,\overline{x_n})=\overline{g(x_1,x_2,\dots,x_n)}$ => $g$ двойственна
$f$ ($f$ и $g$ можно поменять местами, то есть функции $f$ и $g$ двойственны друг другу). Из простейших функций
двойственны друг другу константы 0 и 1, а из законов де Моргана следует двойственность конъюнкции и дизъюнкции.
Тождественная функция, как и функция отрицания, двойственна сама себе (самодвойственная
функция).

Важно: Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится
верное
тождество. В приведённых выше формулах легко найти двойственные друг другу пары

Способ задания булевой функции от n переменных это

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

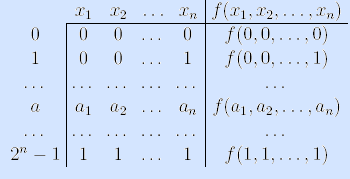
Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

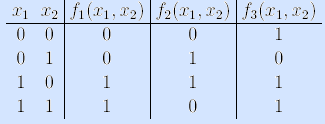
Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f =

n

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f =

n

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = 1, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = 1, I₂, I₃> интервалов:

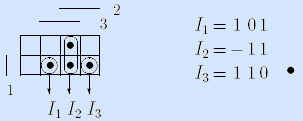
Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = 1, I₂, I₃, I₄> интервалов:

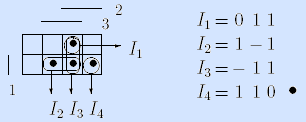
Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I

Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂

₁

Пример. Зададим мажоритарную функцию множеством I»_f = 1 I₂, I₃> всех максимальных интервалов.

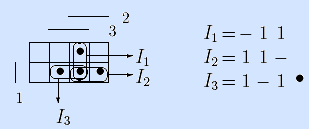
Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Источник

Импликация

Ключевые слова:

• импликация
• исключающее ИЛИ
• эквиваленция

Мы изучили две логические операции с двумя переменными — Ии ИЛИ. Существуют ли другие? И сколько их?

В таблице истинности любой логической операции с двумя переменными всего четыре строки, и эти таблицы отличаются только четырьмя значениями функции в последнем столбце. Поэтому можно придумать всего 16 = 24 различных логических операций с двумя переменными.

На уроках математики вы доказывали теоремы, в которых встречались выражения «если …, то…», «тогда и только тогда, когда…». Эти связки тоже обозначают логические операции, с которыми мы сейчас и познакомимся.

Слово «импликация» означает «следование» — из одного утверждения следует другое. Если истинно первое, то истинно и второе. Например, возьмём высказывание

X = Если идёт дождь, то Лена раскрывает зонтик.

Если ввести обозначения для простых высказываний:

А = Идёт дождь,

В = Лена раскрывает зонтик, то можно записать высказывание X в символьном виде:

X = А → В.

Стрелка вправо обозначает логическую операцию «импликация».

Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «импликация». Что оно означает?

Теперь давайте разберёмся, когда такое высказывание будет истинно, а когда — ложно. Если дождь идёт (А = 1) и Лена раскрывает зонтик (В = 1), то импликация, очевидно, истинна. Если же при дожде Лена зонтик не раскрыла, импликация ложна (из А не следует B!).

А если дождя нет (А = 0)? Тогда о состоянии зонтика Лены мы ничего сказать не можем, потому что он может быть как закрыт, так и открыт. И в обоих случаях импликация будет истинна, потому что не исключено, что из А следует В (возможно, что, когда пойдёт дождь, Лена откроет зонтик). Говорят, что «из истины следует истина, а из лжи — что угодно»

Рис. 2.13

Таблица истинности операции импликация показана на рис. 2.13. Как видим, эта функция равна нулю только при одном значении исходных данных: 1 → 0 = 0, во всех остальных случаях она равна 1.

Обычно, говоря «если…, то…», мы имеем в виду причинно-следственную связь, когда одно вызывает другое. Например, «Если светит солнце, то лужи высыхают» (именно потому, что светит солнце!). Импликация не говорит о причине и следствии, а показывает возможность такой связи. Например, может быть истинной импликация «если сегодня вторник, то Эльбрус покрыт снегом».

Импликация часто используется при решении логических задач. Например, формулировку вида «если А, то В» можно записать как А → В = 1.

Постройте таблицу истинности логической функции В → А 1). Сравните её с таблицей истинности функции А → B. Выполняется ли для импликации переместительный закон (если поменять местами А и B, то результат не изменяется)?

1)В этой и следующих трёх задачах сохраняйте порядок столбцов в таблице истинности: в первом столбце записывайте значение А, во втором — значение B.

Постройте таблицу истинности логической функции А + B. Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы сейчас доказали?

Постройте таблицу истинности логической функции B → А. Сравните её с таблицами истинности известных вам функций с двумя переменными. Какую формулу вы сейчас доказали?

Постройте таблицу истинности логической функции (А → В) и (В → А). Как бы вы назвали эту функцию?

Следующая страница Эквиваленция

Cкачать материалы урока

Способы доказательства тавтологии и следствия

Тавтологией называется тождественно истинное высказывание, верное при любых значениях своих
компонентов. Формула в исчислении высказываний является тавтологией или тождественно
истинной, если её значение для любых значений аргументов истинно.

Примеры тавтологий:

• $ A \to A $ («Из »A» следует »A»»)
• $(A) \lor (\lnot A)$ («»A» или не-»A»»)
• $\overline{P \land \overline P}$.
• $(P \land (P \to Q)) \to Q$
• $A \to (B \to A)$

 Формула F называется тавтологией, или тождественно
истинной формулой, если F истинно при любой интерпретации.

Понятие тавтологии «двойственно»‘ понятию выполнимой формулы: $F$ –
тавтология
тогда и только тогда, когда $\lnot F$ не выполнима. Определение эквивалентных формул, данное выше,
может
быть
переформулировано следующим образом: F эквивалентна G, если F є G – тавтология.

Формула является »тождественно истинной», если она истинна при любых значениях входящих в неё переменных. Вот
несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

1) $ \neg (p \lor q) \leftrightarrow (\neg p \land \neg q)$;

2) $ \neg (p \land q) \leftrightarrow (\neg p \lor \neg q)$;

Закон контрапозиции:

$(p\to q)\leftrightarrow(\neg q\to \neg p)$;

»’Законы поглощения»’:

1) $p\lor(p\land q)\leftrightarrow p$;

2) $p\land(p\lor q)\leftrightarrow p$;

»’Законы дистрибутивности»’:

1) $p\land(q\lor r)\leftrightarrow(p\land q)\lor(p \land r)$;

2) $p\lor(q\land r)\leftrightarrow(p\lor q)\land(p \lor r)$.

Понятие алгебры логики

На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал
английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности
зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том,
что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».

Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их
логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать
любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным
числам в математике.

Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля
представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Пусть функция от
n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта
функция называется логической, или булевой, или переключательной,
или функцией алгебры логики. Описанную функцию часто называют также
булевым вектором. Количество функций от n переменных
равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных
булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов
равно уже .

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или
любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).

На логических элементах, реализующих булевы функции, строятся
логические схемы электронных устройств.

Законы булевой алгебры применяются и в программировании — при написании сложных логических условий
и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь
(это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример —
применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты
все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.

Часто оказывается, что изначально построенное логическое выражение можно упростить,
используя аксиомы, теоремы и законы алгебры логики.

Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта —
минимизация логических функций: общие сведения,
минимизация логических функций: метод непосредственных преобразований и
минимизация логических функций: метод Квайна.

Формальные теории (исчисление)

Формальная теория — результат строгой формализации теории, предполагающей полную абстракцию от
смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно
высказаны
посредством аксиом и правил, позволяющих вывести одну фразу из других.

Формальная теория – это совокупность абстрактных объектов, не связанных с реальным миром, в
котором
представлены правила оперирования множеством символов в строго синтаксической трактовке без учета их смыслового
содержания, т.е. семантики.

Формальная теория считается определенной, если:

• Задано конечное или счётное множество произвольных символов. Конечные последовательности
  символов называются выражениями теории.
• Имеется подмножество выражений, называемых формулами.
• Выделено подмножество формул, называемых аксиомами.
• Имеется конечное множество отношений между формулами, называемых правилами вывода.

Переключательные схемы

Функции проводимости $F$ некоторых переключательных схем:

a)   

Схема не содержит переключателей и проводит ток всегда, следовательно $F=1$;

б)   

Схема содержит один постоянно разомкнутый контакт, следовательно $F=0$;

в)   

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, $F(x) =
x$;

г)    —

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда $х$ замкнут, следовательно, $F(x)
=
\bar
x$;

д)   

Схема проводит ток, когда оба переключателя замкнуты, следовательно, $F(x) = x \land y$;

е)   

Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, $F(x)=x \lor
y$;

ж)   

Схема состоит из двух параллельных ветвей и описывается функцией .

Две схемы называются равносильными, если через одну из них проходит ток тогда и только
тогда, когда он проходит через другую (при одном и том же входном сигнале).

Из двух равносильных схем более простой считается та схема, функция проводимости
которой
содержит меньшее число логических операций или переключателей.

1 Понятие булевой функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество * . Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. * Так мы и приходим к понятию булевой функции.

Определение 1 (Булева функция). Булевой функцией от n аргументов называется функция f из n -ой степени множества в множество .

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству . Множество мы будем в дальнейшем обозначать через B .

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B . При этом алгебра W >, где W – множество всевозможных булевых функций, называется алгеброй логики .

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов

Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

x 1	x 2	.	x n- 1	x n	f
.	f(0,0. 0,0)
.	1	f(0,0. 0,1)
.	1	f(0,0. 1,0)
.	1	1	f(0,0. 1,1)
.	.	.	.	.	.
1	1	.	f(1,1. 0,0)
1	1	.	1	f(1,1. 0,1)
1	1	.	1	f(1,1. 1,0)
1	1	.	1	1	f(1,1. 1,1)

Раз у нас есть стандартный порядок записывания наборов, то для того, чтобы задать функцию, нам достаточно выписать значения f (0,0. 0,0) , f (0,0. 0,1) , f (0,0. 1,0) , f (0,0. 1,1). f (1,1. 0,0) , f (1,1. 0,1) , f (1,1. 1,0) , f (1,1. 1,1). Этот набор называют вектором значений функции .

Таким образом, различных функций n переменных столько, сколько различных двоичных наборов длины 2 n * . А их 2 в степени 2 n .

Множество B содержит два элемента – их можно рассматривать как булевы функции от нуля (пустого множества) переменных – константу 0 и константу 1 .

Функций от одной переменной четыре: это константа 0, константа 1, тождественная функция , т.е. функция, значение которой совпадает с аргументом и так называемая функция « отрицание ». Отрицание будем обозначать символом ¬ как унарную операцию. Приведём таблицы этих четырёх функций:

x	x	¬ x	1
1	1
1	1	1

Как видим, функции от некоторого числа переменных можно рассматривать как функции от большего числа переменных. При этом значения функции не меняется при изменении этих «добавочных» переменных. Такие переменные называются фиктивными , в отличие от остальных – существенных .

Определение 2 (Фиктивные и существенные переменные). Переменная x i называется фиктивной (несущественной) переменной функции f ( x 1 ,···,x n ), если f ( x 1 ,···,x i- 1 ,0 ,x i+ 1 ,···,x n ) = f ( x 1 ,···,x i- 1 ,1 ,x i+ 1 ,···,x n ) для любых значений x 1 ,···,x i- 1 ,x i+ 1 ,···,x n . Иначе переменная x i называется существенной .

Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:

x 1	x 2	x 1 & x 2	x 1 Ъ x 2	x 1 Й x 2	x 1 Е x 2	x 1 є x 2	x 1 | x 2
1	1
1	1	1	1	1
1	1	1	1
1	1	1	1	1	1	1

Эти функции записываются как бинарные операции в инфиксной нотации. x 1 & x 2 называется конъюнкцией , x 1 Ъ x 2 – дизъюнкцией , x 1 Й x 2 – импликацией , x 1 є x 2 – эквивалентностью , x 1 Е x 2 – суммой по модулю 2 , x 1 | x 2 – штрихом Шеффера .

Значения 0 и 1 часто интерпретируют как «ложь» и «истину». Тогда понятным становится название функции «отрицание» – она меняет «ложь» на «истину», а «истину» на «ложь». Отрицание читается как «не». Конъюнкция читается обычно как «и» – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная. * Кроме x 1 & x 2 часто используют обозначение x 1 Щ x 2 или x 1 · x 2 или x 1 x 2 или min( x 1 ,x 2 ). Дизъюнкция читается «или» – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная. * Импликация выражает факт, что из x 1 следует x 2 . * Импликацию часто также обозначают x 1 x 2 .

Решение заданий ЕГЭ с помощью Python

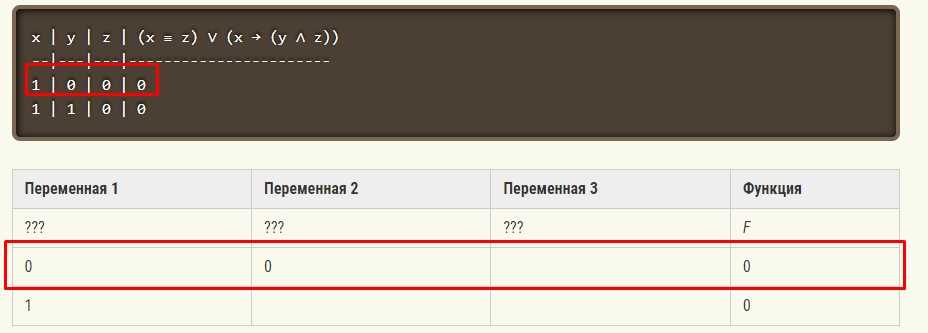
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

Переменная 1	Переменная 2	Переменная 3	Функция
???	???	???	F
1

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала  — буква, соответствующая первому столбцу; затем  — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Переменная 1	Переменная 2	Функция
???	???	F
1

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Для построения таблицы истинности данного логического выражения можно воспользоваться языком программирования Python и его возможностью работы с логическими операциями. Для этого можно написать следующий код:

В данном коде мы задаем начальные значения переменных x, y и z как False. Затем мы выводим заголовок таблицы истинности и перебираем все возможные значения переменных x, y и z, используя вложенные циклы. Для каждой комбинации значений переменных мы вычисляем значение выражения и выводим результат в таблицу. В конце каждой строки таблицы мы переходим на новую строку с помощью команды .

Результатом выполнения данного кода будет таблица истинности для данного логического выражения:

Как можно видеть из таблицы, значение данного логического выражения будет равно 1 (True) только в тех случаях, когда x и z равны, или когда x равно True, а y и z также равны True. В остальных случаях, значение выражения будет равно 0 (False).

Фильтруем таблицу истинности

Для анализа таблицы, нам нужны только те значения итогового выражения, которые принимают значение , потому что в задании, для расшифровки, приведен фрагмент только с ложными значениями выражения.

Для этого, внутри переборной конструкции из трех циклов , сначала вычисляется значение логического выражения, а потом добавлено условие:

В случае, если итоговое выражение (переменная ), имеет ложное значение, мы печатаем фрагмент таблицы истинности.

Сопоставляем получившийся фрагмент из программы и задания

Шаг 1. Сравниваем две таблицы: получившуюся с помощью программы и фрагмента, данного в задании.

Сравнивая две таблицы, мы видим только одну строку, где две исходных переменных одновременно равны 0 (False). Только значение переменной3 пусто. Значит, можно сделать вывод, что — это .

Шаг 2. Оставшаяся строка фрагмента из задания, содержит только одно значение — 1 ().

Ей соответствует нижняя строка результатов программы. Переменную , мы исключаем, так как нашли ее на шаге 1. Значит — — это , так как именно у нее значение (). Оставшаяся соответствует переменной .

Ответ: