Диагональ треугольника

Как найти длину основания: простое объяснение

Длина основания треугольника является одним из его важных параметров. Она определяет ширину треугольника и играет важную роль при вычислении его площади и других характеристик.

Чтобы найти длину основания треугольника, вам понадобится знать другие известные параметры треугольника, такие как его высота, площадь или другие стороны и углы. Здесь представлены несколько простых методов для определения длины основания:

Использование площади треугольника: Если у вас есть известная площадь треугольника и его высота, то длина основания может быть найдена по формуле: основание = 2 * площадь / высота.
Использование длин других сторон: Если у вас есть известны длины двух других сторон треугольника и угол между ними, то длина основания может быть найдена с помощью теоремы косинусов. Данная формула имеет вид: основание = √(сумма квадратов длин двух сторон — 2 * длина первой стороны * длина второй стороны * cos(угол между ними)).

Важно помнить, что для применения этих формул вам нужно знать значения других параметров треугольника. Если у вас есть несколько известных значений, вы можете использовать различные методы и формулы для нахождения длины основания

Надеемся, что эта информация поможет вам легко определить длину основания треугольника!

Как определить диагональ равнобедренного треугольника через радиус описанной окружности

При изучении геометрии равнобедренного треугольника часто возникает вопрос о возможности определения диагонали этого треугольника через радиус описанной окружности. И на самом деле, существует формула, которая позволяет нам легко найти эту диагональ.

Диагональ равнобедренного треугольника, проходящая через его вершину и перпендикулярная его основанию, называется высотой. Возьмем данную высоту и обозначим ее буквой h.

Известно, что равнобедренный треугольник имеет две одинаковых стороны, которые являются основанием. Обозначим это основание буквой b.

Также, в равнобедренном треугольнике, соединяющая вершину и середину основания, называется медианой и обозначается буквой m.

Используя формулу для длины медианы в равнобедренном треугольнике, которая равна половине длины высоты, мы можем найти значение медианы.

Далее, используя связь между медианой и радиусом описанной окружности, которая устанавливает, что медиана равнобедренного треугольника равна половине диагонали треугольника, проходящей через середину основания и точку касания описанной окружности с основанием, мы можем найти длину диагонали.

Таким образом, диагональ равнобедренного треугольника, проходящая через середину основания и точку касания описанной окружности с основанием, равна удвоенному значению радиуса описанной окружности.

Эта формула позволяет легко и быстро определить длину диагонали равнобедренного треугольника и является полезной для решения задач, связанных с этим геометрическим объектом.

Определение и понятие диагонали основания

В геометрии диагональ основания относится к фигурам, таким как треугольник, прямоугольник и параллелограмм. Диагональ — это линия, которая соединяет вершины фигуры или точки пересечения сторон. В случае треугольника, диагональ основания — это линия, соединяющая две вершины треугольника, не являющиеся вершинами основания.

Диагональ основания имеет ряд важных свойств и применений в геометрии. Во-первых, она является одной из сторон треугольника и может быть использована для решения задач по нахождению площади, периметра и других характеристик треугольника. Она также может быть использована для определения типа треугольника, например, равносторонний, равнобедренный или разносторонний.

В случае прямоугольника диагональ основания делит его на два прямоугольных треугольника и может быть использована для определения его площади и периметра. Она также является диагональю параллелограмма и может быть использована для определения его свойств и характеристик, таких как площадь и углы.

Диагональ основания также имеет важное значение в контексте теоремы Пифагора. В прямоугольном треугольнике диагональ основания является гипотенузой, а катеты — сторонами треугольника

Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов катетов.

В заключение, диагональ основания играет важную роль в геометрии и используется для определения и вычисления различных свойств и характеристик фигур, таких как треугольник, прямоугольник и параллелограмм. Понимание и использование диагонали основания помогает в решении геометрических задач и построении моделей в реальном мире.

Другие связанные цифры

Есть еще три окружности, касательные одновременно к трем линиям, имеющим стороны треугольника, и все три находятся за пределами этого треугольника. Точки пересечения этих окружностей со сторонами треугольника образуют треугольник Нагеля. Отрезки, соединяющие эти точки контакта с противоположными вершинами треугольника, совпадают в точке, называемой точкой Нагеля.

Окружность, диаметр которой соединяет точку Нагеля с ортоцентром, называется окружностью Фурмана, а ее радиус равен расстоянию между центрами вписанной и описанной окружностей.

Центры трех окружностей образуют треугольник Бевана, который гомотетичен треугольнику Жергонна. Центр описанной окружности называется точкой Бевана.

Три описанных выше окружности касаются изнутри окружности, называемой окружностью Аполлония. Линии, соединяющие точки соприкосновения с противоположными вершинами треугольника, совпадают в точке, называемой точкой Аполлония.

Вписанная окружность и три выписанных окружности касаются окружности Эйлера. Точки соприкосновения называются точками Фейербаха.

Симедианы и точка Лемуана

Симедиана представляет собой линию симметрична по отношению к среднему по отношению к биссектрисе из одной и той же вершины. Три симедианы совпадают в точке, называемой точкой Лемуана.

Точка Ферма

В прямоугольном треугольнике есть одна точка, которая минимизирует сумму расстояний до вершин. В этой точке, называемой точкой Ферма , углы, образованные сегментами к вершинам треугольника, равны 120 °.

Точки, линия и круг Брокара

Очки Брокара.

Если треугольник не плоский, существуют две точки, называемые точками Брокара, для которых отрезки по направлению к вершинам подразделяют треугольник на три треугольника, имеющих угол одинаковой меры, путем перестановки вершин исходного треугольника. Тогда величина этого угла будет одинаковой для двух точек.

Линия Брокара — это линия, проходящая через эти две точки.

Точки Брокара принадлежат окружности Брокара , диаметр которой имеет на концах центр описанной окружности и точку Лемуана.

Согласно теореме Аласии , линия Брокара параллельна одной из сторон тогда и только тогда, когда треугольник равнобедренный с этой стороной в качестве основания.

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Что такое основание прямоугольника и как его определить

Определить основание прямоугольника можно, измерив его длину или ширину с помощью линейки или мерного инструмента.

Основание прямоугольника является одним из его основных параметров и определяет его форму и размеры.

Длина основания прямоугольника обозначается буквой «a», а ширина — буквой «b».

Определение основания прямоугольника имеет важное практическое значение в различных областях,

таких как геометрия, строительство, дизайн и архитектура. Знание основы прямоугольника позволяет рассчитывать его площадь, периметр и другие характеристики.

Основание прямоугольника также влияет на его визуальное восприятие и функциональность.

На основе выбранного основания можно создавать различные формы и конструкции,

обладающие определенными эстетическими и функциональными особенностями.

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P={n(n-3)\over{2}}$ – где n это число сторон многоугольника.

Проверим для квадрата:

$P={4(4-3)\over{2}}={4\over2}=2$ – все верно.

Рис. 3. Диагонали квадрата.

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.

/5

Вопрос 1 из 5

Понятие длины основания треугольника

Длина основания треугольника является одной из важных характеристик этой геометрической фигуры. Она определяется как расстояние между двумя вершинами треугольника, которые соединены отрезком и называются «основанием». Основание может быть горизонтальным или наклонным, в зависимости от положения треугольника.

Длина основания является одним из определяющих параметров треугольника и влияет на его форму и свойства. Она позволяет определить площадь треугольника, а также ряд других характеристик, таких как высота и биссектриса.

Длина основания треугольника может быть измерена с помощью линейки или другого инструмента для измерения расстояний. В некоторых случаях она может быть вычислена с использованием других известных параметров треугольника, таких как углы или длины сторон.

В геометрии основание треугольника обычно обозначается буквой «b». Когда рассматривается прямоугольный треугольник, горизонтальное основание называется «основанием прямоугольника».

Свойства основания треугольника:

Основание треугольника играет ключевую роль в его определении и влияет на множество его свойств. На самом деле, основание является основой всего треугольника (вот такое интересное замечание!). Ведь оно не только определяет его форму, но и влияет на другие важные характеристики треугольника.

Свойство 1: Основание определяет тип треугольника

Первое свойство основания треугольника заключается в том, что оно помогает нам определить тип треугольника. Как это происходит? Если у треугольника все три стороны равны, то это равносторонний треугольник. И в этом случае все три стороны являются его основанием. Если две стороны равны, то это равнобедренный треугольник, и одна из равных сторон является его основанием. Если все три стороны разные, то это разносторонний треугольник и в таком случае любая из его сторон может быть основанием. Такая интересная возможность определять тип треугольника только по его основанию!

Свойство 2: Высота треугольника проходит через основание

Второе необычное свойство основания треугольника – это то, что его основание определяет высоту треугольника. Что значит высота треугольника? Это перпендикуляр, опущенный из вершины треугольника на его основание. И именно это основание служит осью, через которую проходит высота и разделяет треугольник на два равных подтреугольника. Если основание меняется, то меняется и высота треугольника. Не так ли это замечательно?

Свойство 3: Основание влияет на площадь треугольника

Третье свойство основания треугольника – это его влияние на площадь треугольника. Площадь треугольника рассчитывается по формуле: площадь = (основание * высота) / 2. Как видите, в формуле присутствует и основание треугольника. Это означает, что при изменении основания, меняется и площадь треугольника. И вот тут возникает интересный вопрос: что будет с площадью треугольника, если его основание удлинить или укоротить? Подумайте и найдите самостоятельно ответ на этот вопрос!

Вот они – уникальные свойства основания треугольника! Основание определяет его тип, проходит через него высота и влияет на его площадь

Это важное и захватывающее путешествие в мир геометрии треугольников. Что ж, продолжайте исследовать и открывать все новые и удивительные свойства геометрических фигур!

Что такое призма — понятие в геометрии

Многоугольник, который лежит в основании призмы, напрямую обуславливает наименование призмы. Так, если основанием является треугольник, то перед нами треугольная призма, если четырехугольник, то перед нами четырехугольная призма, а если пятиугольник, то перед нами пентапризма и так далее.

Призма состоит из следующих элементов:

Оснований.
Боковых граней.
Боковой поверхности.
Полной поверхности.
Боковых ребер.
Высоты.
Диагонали.
Диагональной плоскости.
Диагонального сечения.
Перпендикулярного сечения.

Рассмотрим каждый элемент подробно. Перед вами чертеж призмы:

Определение основания треугольника

Чтобы понять, что такое основание треугольника, представь себе строительную леску. Когда строитель поднимает эту леску, его помощник удерживает один конец, а другой конец (основание) опирается на землю. Точно так же и в треугольнике — одна сторона (основание) лежит на этаже, а высота проходит от этой стороны до вершины.

Какими свойствами оснащено основание? Основание треугольника должно быть хорошо определено чтобы избежать путаницы со сторонами треугольника. Основание может быть любой из трех сторон треугольника, но при этом нужно указывать какая именно сторона является основанием.

Как например, в треугольнике ABC, мы можем назвать сторону AB как основание, а потом говорить о высоте, опирающейся на это основание

Важно понимать, что выбор основания остается за нами и зависит от того, какая информация важна в конкретной ситуации

В основном, основание выбирается в зависимости от специфической геометрической задачи, которую мы пытаемся решить или от того, какую информацию мы хотим получить о треугольнике. В рабочих координатах, основание треугольника может быть любой стороной треугольника, и в таком случае мы будем обозначать его длиной как «b».

Зная определение и свойства основания треугольника, становится проще решать задачи и углубляться в геометрию. Не бойся экспериментировать с разными треугольниками и их основаниями! Ведь, как говорят, «геометрия — это игра с формами и пространством». Путешествуй в этом увлекательном мире и строй свои треугольники с яркой и уникальной основой!

Как выбрать правильную диагональ основания для конкретных измерений?

Диагональ основания — это один из важнейших параметров, которые нужно учитывать при выборе измерительного прибора для конкретной задачи. В зависимости от выбранной диагонали основания, могут различаться точность и удобство измерений.

При выборе диагонали основания следует руководствоваться следующими принципами:

Учитывайте размеры измеряемых объектов. Если вы планируете измерять небольшие объекты, то достаточно выбрать маленькую диагональ основания, чтобы гарантировать точность измерений.
Задумайтесь о доступности измеряемой поверхности. Если планируется измерение в труднодоступных местах, то имеет смысл выбрать прибор с маленькой диагональю основания, чтобы его проще было разместить на объекте и снять измерения.
Учтите требуемую точность. Если измерение требует высокой точности, необходимо выбрать измерительный прибор с большей диагональю основания, так как это обеспечит более точные результаты.
Оцените бюджетные ограничения. При выборе прибора с большой диагональю основания обычно стоимость выше, поэтому следует оценить свои финансовые возможности и выбрать прибор соответственно.

Учитывая эти принципы, вы сможете определить оптимальную диагональ основания для конкретных измерений. Берегите время и деньги, выбирая правильно!

math-public:trapeciya [Президентский ФМЛ №239]

math-public:trapeciya

Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.

Сумма углов при боковой стороне трапеции равна $180^circ$.

Действительно, так как основания трапеции параллельны, а боковая
сторона является секущей, то углы при боковой стороне являются
внутренними односторонними углами при параллельных прямых, и,
следовательно, их сумма равна $180^circ$.

Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция называется прямоугольной, если один из ее углов равен $90^circ$.

Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны.
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.

Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $angle A=angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $ riangle ABE$ и $ riangle CFD$ равны по катету и гипотенузе ($AB=CD,
BE=CF$).
Следовательно, $angle A=angle D$.

В равнобедренной трапеции $ABCD$ рассмотрим треугольники $ riangle ABD$ и $ riangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $angle A=angle D$ по
первому пункту).
Следовательно, $AC=BD$.

Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $ riangle AOD$ и $ riangle BOC$ – равнобедренные, а треугольники $ riangle AOB$ и $ riangle COD$ равны.

Действительно, во втором пункте уже было доказано, что $ riangle ABD= riangle ACD$.
Следовательно, $angle 1=angle 2$, а так как они накрест лежащие с углами $angle 3$ и $angle 4$ соответственно, то $angle 3=angle 4$, что
и означает, что треугольники $ riangle AOD$ и $ riangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $ riangle AOB= riangle COD$ по
третьему признаку равенства треугольников.

Так как $ riangle AEB= riangle CFD$ (по катету и
гипотенузе), то $AE=FD$.

Кроме того, $EF=BC$, следовательно, $AE=dfrac{AD-BC}{2}$ и
$AF=dfrac{AD-BC}{2}+BC=dfrac{AD+BC}{2}$.

Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.

Рассмотрим трапецию $ABCD$, в которой $angle A=angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $angle A=angle CED$, как соответственные углы.
Следовательно, $angle CED=angle D$, а тогда $ riangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.

Рассмотрим трапецию $ABCD$, у которой $AC=BD$.

Докажем, что тогда $AB=CD$.

Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.

Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $ riangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $angle OAD=angle ODA$, и $ riangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $ riangle BOA= riangle COD$ по первому признаку ($angle BOA=angle COD$ — как вертикальные).
Следовательно, $AB=CD$.

В равнобедренной трапеции со взаимно перпендикулярными диагоналями
высота равна средней линии.

Рассмотрим равнобедренную трапецию $ABCD$, в которой $ACperp BD$.

Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.

Действительно, $ riangle AOD$ – равнобедренный и прямоугольный, следовательно, $angle OAD = 45^circ$. Тогда $ riangle AHC$ – равнобедренный, то есть $AH=CH$.

Но отрезок $AH$ равен полусумме оснований.

math-public/trapeciya.txt · Последние изменения: 2016/04/13 23:56 — labreslav

Почему необходимо знать длину основания

Длина основания является одним из важных параметров треугольника. Она определяет форму и размеры треугольника, и знание этого значения позволяет решать различные задачи и выполнять геометрические вычисления.

Знание длины основания треугольника позволяет:

Вычислять площадь треугольника. Площадь треугольника равна половине произведения длины основания на высоту, опущенную из вершины треугольника на основание. Зная длину основания, можно легко вычислить площадь треугольника по формуле.
Определять тип треугольника. Зная длину основания и длины двух других сторон, можно определить тип треугольника (равносторонний, равнобедренный или разносторонний).
Решать задачи на нахождение высоты треугольника. Зная длину основания и площадь треугольника, можно вычислить высоту, опущенную из вершины на основание треугольника.
Определять другие параметры треугольника. Зная длину основания и другие стороны треугольника, можно вычислить его периметр, углы и другие характеристики.

Поэтому знание длины основания треугольника является важным для решения геометрических задач и выполнения различных вычислений, связанных с треугольниками.

Определение равнобедренного треугольника

Основные особенности равнобедренного треугольника:

У него две равные стороны, называемые равными боковыми сторонами;
Угол, образованный между равными боковыми сторонами и третьей стороной, называется вершинным;
В равнобедренном треугольнике углы, противолежащие равным боковым сторонам, равны между собой;
Основание равнобедренного треугольника — это третья сторона, которая отличается от равных боковых сторон.

Для определения равнобедренного треугольника можно проверить равенство двух сторон. Если две стороны треугольника равны между собой, а третья сторона отличается по длине, то треугольник является равнобедренным.

Диагональ основания: суть и влияние на измерение

Диагональ основания — это расстояние между двумя противоположными углами основания. В контексте измерения оно играет важную роль и имеет влияние на точность результатов.

Для начала, давайте разберемся, что такое основание. В контексте геометрии основание часто относится к стороне или отрезку, на котором располагается фигура или объект. Диагональ же основания представляет собой линию, которая соединяет две противоположные вершины этого основания.

Почему диагональ основания важна при измерении? Дело в том, что при использовании диагонали основания мы учитываем дополнительную точку измерения, которая может повысить точность и надежность результатов.

Рассмотрим пример. Представьте себе треугольник с основанием, одна из вершин которого помечена точкой A, а противоположная вершина — точкой B. Если мы измерим длину основания только прямой линией от точки А до точки B, мы получим один результат. Однако, если мы измерим длину основания при помощи диагонали, то учтем проекцию диагонали, что может дать более точную оценку.

Диагональ основания также имеет значительное влияние на измерение, когда основание является наклонным или кривым. В этом случае, только диагональ основания может точно охватить все изменения и несовершенства формы.

Однако, важно отметить, что при измерении диагонали основания необходимо быть осторожными и аккуратными. Небольшая неточность или ошибочное измерение может существенно повлиять на результаты и искажение данных

В заключении, диагональ основания является важным понятием в контексте измерения, особенно при работе с наклонными или кривыми основаниями. Она позволяет получить более точные и надежные результаты измерений, однако требует аккуратности и внимания к деталям.

Что делать на практике

Строительство любого здания начинается с фундамента, а фундамент – с разметки на земле. Если сделать её точно, то поддерживать правильную форму возводимых конструкций станет делом техники: нужно будет просто постоянно контролировать вертикальный и горизонтальный уровень каждого элемента.

Как сделать точную разметку

Даже если основание дома имеет сложную форму, его можно разбить на прямоугольники и другие простые фигуры.

Для такого основания делается разметка двух прямоугольников и трапеции

Как узнать диагональ треугольника по двум сторонам, мы знаем, длину этих сторон берем из проекта. Полученная цифра вам понадобится, чтобы убедиться в точности сделанной разметки путем сравнения двух диагоналей.

Опущу описание самого процесса разметки фундамента на земле с помощью шнура и колышков. Расскажу лишь, как выставить прямые углы. С этой задачей легко справлялись даже древние египтяне, жившие задолго до Пифагора и не знавшие математики. Они брали длинную бечевку и завязывали на ней 13 узелков на равном расстоянии друг от друга, получая 12 одинаковых отрезков. И натягивали её вокруг трех колышков так, чтобы на одной стороне было 3 отрезка, на второй 4, а 13-тый узелок точно совпадал с первым. Добивались этого, переставляя колышки до достижения нужного результата.

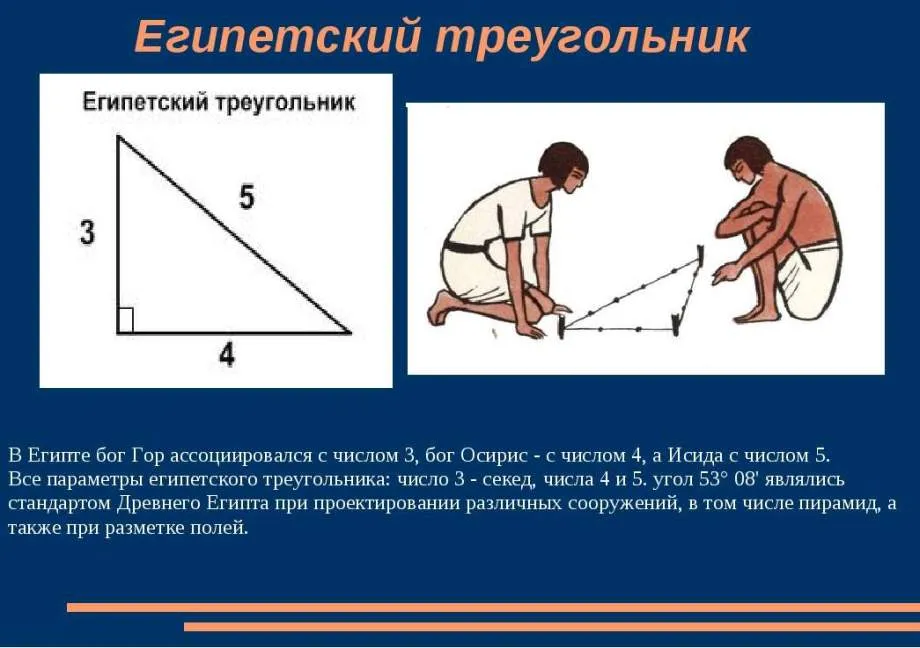Этот способ и сейчас носит название египетского треугольника

А нужный результат – это прямой угол между двумя короткими сторонами. На практике поступаем так:

вбиваем колышек в точку, где будет один из углов дома;
в стороны от него примерно под прямым углом натягиваем шнур;

Колышек должен быть хорошо зафиксирован

на одной стороне нужно отложить 3 м, на второй 4 м, поставить метки и измерить диагональ между ними;
если она не равна 5 м, изменяем угол между шнурами и повторяем измерения до тех пор, пока не получим нужное значение.

Выставив один угол, отмечают на шнурах длину смежных стен, и в этих точках повторяют процедуру для остальных углов. Если все они будут прямыми, а длины противоположных сторон равными, диагонали должны сойтись.

Проверка диагоналей

Перед тем как проверить диагональ, нужно убрать высокую траву и отвалы земли внутри разметки, чтобы ничто не препятствовало измерениям. А затем с помощью рулетки измерить расстояния между противоположными вершинами прямоугольника. Допускается разница между двумя диагоналями в пределах 1-1,5 см в зависимости от параметров фундамента.

Важно!

Измерять нужно и по внешним, и по внутренним углам разметки.

В этом видео описан самый простой способ вычисления диагонали:

Если расхождение значительное при том, что параллельные стороны одинаковы по длине, значит, вы допустили погрешность при разметке. Чтобы выпрямить углы параллелограмма (см. рис. выше), точки В и С смещаются влево примерно на половину размера расхождения. Затем снова находится диагональ АС и ВD, если их значения не сравнялись, смещение вершин в ту или иную сторону повторяют.

Из чего состоит основание треугольника

Основание треугольника — это одна из сторон этой геометрической фигуры. Треугольник состоит из трех сторон и трех углов.

Основание является нижней стороной треугольника и примыкает к его двум углам. На основании треугольника можно определить его другие элементы, такие как высота и площадь.

Для прямоугольного треугольника одна из его сторон является основанием. Для остроугольного или тупоугольного треугольника, основание может быть любой из его сторон.

Измерение основания треугольника может быть важным при решении различных задач и расчетах, связанных с этой фигурой.

Основание треугольника может быть изображено на плоскости с помощью графических инструментов или указано числовым значением в расчетах.

Свойства треугольников

Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.

Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.

Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.

Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.

Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.

Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.

Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.

Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.

Следующие две теоремы рассматривают свойства для равнобедренных треугольников.

Углы при основании равнобедренного треугольника будут равными.

Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.

Замечание 1

Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.