Погрешность, точность и разрешение

Неточность измерения

Неточности измерения могут быть разделены на систематические и случайные измерительные ошибки. Систематические ошибки вызваны отклонениями при усилении и настройкой «нуля» измерительного оборудования. Случайные ошибки вызваны шумом и индуцированными напряжениями и/или токами.

Погрешность и точность

Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением. Точность относится к случайному разбросу измеряемых величин.

Когда мы проводим некоторое число измерений до момента стабилизации напряжения или же какого-то другого параметра, то в измеренных значениях будет наблюдаться некоторая вариация. Это вызвано тепловым шумом в измерительной цепи измерительного оборудования и измерительной установки. Ниже, на левом графике показаны эти изменения.

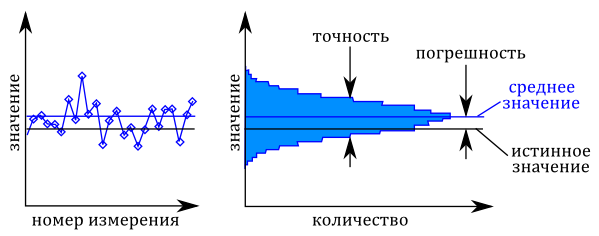Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.

Гистограмма

Измеренные значения могут быть изображены в виде гистограммы, как показано справа на рисунке. Гистограмма показывает, как часто наблюдается измеренное значение. Самая высокая точка на гистограмме, это чаще всего наблюдаемое измеренное значение, в случае симметричного распределения равно среднему значению (изображено синей линии на обоих графиках). Черная линия представляет истинное значение параметра. Разница между средним измеренной величины и истинным значением и является погрешностью. Ширина гистограммы показывает разброс отдельных измерений. Этот разброс измерений называется точностью.

Используйте правильные термины

Погрешность и точность, таким образом, имеют различные значения. Поэтому вполне возможно, что измерение является очень точным, но имеющим погрешность. Или наоборот, с малой погрешностью, но не точное. В общем, измерение считается достоверным, если оно точное, и с малой погрешностью.

Абсолютная погрешность

Абсолютной погрешностью числа
называют разницу между этим числом и его точным значением.Рассмотрим пример

: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным

Поэтому в практике более важное значение имеет определение относительной погрешности измерения

Записывают абсолютную погрешность числа, используя знак ±. Например

, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Погрешность

Погрешность является индикатором корректности измерения. Из-за того, что в одном измерении точность оказывает влияние на погрешность, то учитывается среднее серии измерений.

Погрешность измерительного прибора обычно задается двумя значениями: погрешностью показания и погрешностью по всей шкале. Эти две характеристики вместе определяют общую погрешность измерения. Эти значения погрешности измерения указываются в процентах или в ppm (parts per million, частей на миллион) относительно действуюшего национального стандарта. 1% соответствует 10000 ppm.

Погрешность приводится для указанных температурных диапазонов и для определенного периода времени после калибровки

Обратите внимание, что в разных диапазонах, возможны, и различные погрешности

Погрешность показаний

Указание процентного отклонения без дополнительной спецификации также относится к показанию. Допустимые отклонения делителей напряжения, точность усиления и абсолютные отклонения при считывании и оцифровке являются причинами этой погрешности.

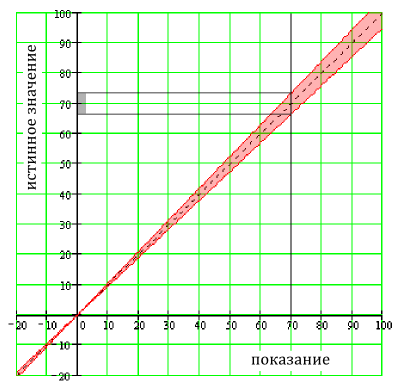Неточность показаний в 5% для значения 70 В

Вольтметр, который показывает 70.00 В и имеет спецификацию «± 5% от показаний», будет обладать погрешностью в ±3.5 В (5% от 70 В). Фактическое напряжение будет лежать между 66.5 и 73.5 вольтами.

Погрешность по всей шкале

Этот тип погрешности обусловлен ошибками смещения и ошибками линейности усилителей. Для приборов, которые оцифровывают сигналы, присутствует нелинейность преобразования и погрешности АЦП. Эта характеристика относится ко всему используемому диапазону измерений.

Вольтметр может иметь характеристику «3% шкалы». Если во время измерения выбран диапазон 100 В (равный полной шкале), то погрешность составляет 3% от 100 В = 3 В независимо от измеренного напряжения. Если показание в этом диапазоне 70 В, то реальное напряжение лежит между 67 и 73 вольтами.

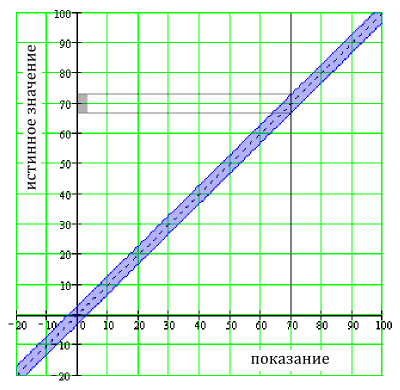Погрешность 3% шкалы в диапазоне 100 В

Из приведенного выше рисунка ясно, что этот тип допустимых отклонений не зависит от показаний. При показании 0 В реальное напряжение лежит между -3 и 3 вольтами.

Погрешность шкалы в цифрах

Часто для цифровых мультиметров приводится погрешность шкалы в разрядах вместо процентного значения.

У цифрового мультиметра с 3½ разрядным дисплеем (диапазон от -1999 до 1999), в спецификации может быть указано «+ 2 цифры». Это означает, что погрешность показания 2 единицы. Например: если выбирается диапазон 20 вольт (± 19.99), то погрешность шкалы составляет ±0.02 В. На дисплее отображается значение 10.00, а фактическое значение будет между 9.98 и 10.02 вольтами.

Вычисление погрешности измерения

Спецификации допустимых отклонений показания и шкалы вместе определяют полную погрешность измерения прибора. Ниже при расчете используются те же значения, что и в приведенных выше примерах:

Точность: ±5% показания (3% шкалы)

Диапазон: 100 В

Показание: 70 В

Полная погрешность измерения вычисляется следующим образом:

В этом случае, полная погрешность ±6.5В. Истинное значение лежит между 63.5 и 76.5 вольтами. На рисунке ниже это показано графически.

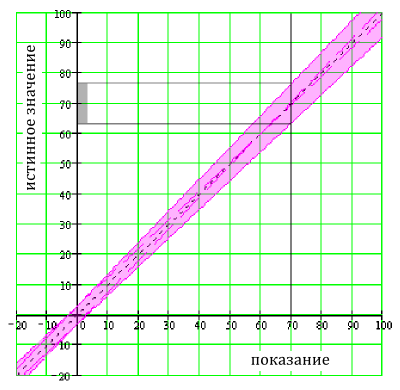Полная неточность для неточностей показания 5% и 3% шкалы для диапазона 100 В и показания 70 В

Процентная погрешность — это отношение погрешности к показанию. Для нашего случая:

Цифры

Цифровые мультиметры могут иметь спецификацию «± 2.0% показания, + 4 цифры». Это означает, что 4 цифры должны быть добавлены к 2% погрешности показания. В качестве примера снова рассмотрим 3½ разрядный цифровой индикатор. Он показывает 5.00 В для выбранного диапазона 20 В. 2% показания будет означать погрешность в 0,1 В. Добавьте к этому численную погрешность  (= 0,04 В). Общая погрешность, следовательно, 0,14 В. Истинное значение должно быть в диапазоне между 4.86 и 5,14 вольтами.

Решенные примеры по погрешности

Пример 1. Случайная выборка из 50 студентов имеет средние карманные деньги 2500 и стандартное отклонение 567. Найдите погрешность, если c = 0,95.

Решение:

Пример 2: Было опрошено 600 студентов, и было обнаружено, что средний CGPA учащихся составил 8,7 при стандартном отклонении населения 0,2. Рассчитайте погрешность для уровня достоверности 90%.

Решение:

Пример 3: В ходе опроса было обнаружено, что средняя заработная плата 5000 сотрудников составляет 350000 со стандартным отклонением населения 0,3. Какова погрешность при доверительном уровне 99%?

Решение:

Пример 4: Найдите погрешность при опросе населения в 400 человек.

Решение:

Значимость предельной погрешности измерения

Значимость предельной погрешности связана с необходимостью получать достоверные и точные данные. Она играет важную роль во многих сферах деятельности, таких как научные исследования, инженерное проектирование, медицинская диагностика и производство. Ошибки измерений могут привести к неправильным выводам или решениям, что может иметь серьезные последствия.

Применение предельной погрешности измерения позволяет контролировать качество измерений и оценивать достоверность полученных результатов. Она помогает определить, насколько можно доверять полученным данным и какие выводы можно сделать на основе этих данных.

Определение предельной погрешности является важной задачей при разработке и испытаниях измерительного оборудования. Она должна быть учтена при проведении измерений и использовании измерительных приборов

Знание предельной погрешности позволяет выбирать среди различных измерительных приборов тот, который обеспечивает требуемую точность и достоверность измерений.

Примеры применения предельной погрешности1

В медицинской диагностике предельная погрешность измерения имеет важное значение, так как от нее зависит правильность постановки диагноза и назначение лечения. Например, при измерении уровня глюкозы в крови предельная погрешность должна быть минимальной, чтобы полученные результаты были достоверными и помогли принять правильные медицинские решения.2

В производственных процессах предельная погрешность измерения используется для контроля качества продукции. Например, при изготовлении электронных компонентов, предельная погрешность при измерении их характеристик помогает оценить соответствие продукции требованиям и стандартам. Это позволяет выявить бракованные детали и предотвратить проблемы в дальнейшем.3. В научных исследованиях предельная погрешность измерения является важным фактором, определяющим достоверность полученных результатов. Например, при измерении физических величин, таких как скорость, сила или температура, предельная погрешность позволяет оценить точность измерений и учесть ее при анализе полученных данных.

Определения

Есть верхний и нижний предел погрешности. Обычно оба имеют одинаковый размер и в таком случае называются пределами симметричной погрешности . Пределы погрешности — это всегда суммы, поэтому они указываются без знака.г{\ displaystyle G}

Это относится к (абсолютному) отклонению или (абсолютной) ошибке. Ф.{\ displaystyle F}

|Ф.|≤г{\ displaystyle | F | \ leq G} .

Соответственно, существует относительный предел ошибки таким образом, что относительное отклонение или относительная погрешность применяется
г{\ displaystyle g}ж{\ displaystyle f}

|ж|≤г{\ displaystyle | f | \ leq g} .

Контрольное значение для относительной погрешности подобно правильного значения  ;
Икср{\ displaystyle x_ {r}}

гзнак равног|Икср|{\ displaystyle g = G / | x_ {r} |} .

Методы определения и учета

Для определения допустимой погрешности в процессе измерений применяются различные методы и подходы. Основные методы определения допустимой погрешности включают следующие:

1. Стандартные методы: при использовании стандартных методов определения допустимой погрешности учитываются стандартные требования и нормативные документы, которые предписывают требования к точности измерений в соответствующей области.
2. Методы, основанные на оценке ошибок прибора: в данном случае допустимая погрешность рассчитывается на основе известных ошибок и характеристик используемого прибора.
3. Статистические методы: статистические методы определения допустимой погрешности позволяют учитывать случайные факторы и представляют собой математические модели, которые учитывают распределение вероятностей погрешностей.

Помимо методов определения допустимой погрешности, также существуют методы учета погрешностей, которые позволяют учесть особенности конкретного измерительного процесса и уменьшить влияние погрешностей. Некоторые из них:

• Компенсационный метод: при использовании этого метода погрешность измерений устраняется или уменьшается путем применения корректирующих факторов или компенсирующих процедур.
• Методический метод: этот метод предусматривает разработку и применение специальных методик измерения, которые позволяют минимизировать влияние погрешностей и повысить точность измерений.
• Априорный метод: этот метод предусматривает учет известных факторов и погрешностей заранее, до проведения измерений, путем проведения априорного анализа и предварительной оценки.

В целом, выбор метода определения и учета допустимой погрешности в каждом конкретном случае зависит от специфики измерений, требований к точности, наличия и характера погрешностей прибора и других факторов.

Допустимые нормы расхождения

При проведении межевых работ по уточнению границ земельного надела или при определении места границ вновь образуемых наделов при выделе или разделе участков могут возникнуть расхождения значений площадей
между отображённой в и вновь рассчитанной.

ВНИМАНИЕ!
Рассчитанная площадь надела земли с уточнёнными границами не может превышать площадь данного надела, указанную в кадастровых документах больше, чем на предельный минимальный размер земельного надела, установленный законом для данного вида земли. Минимальные размеры устанавливаются региональными и муниципальными нормативными актами с небольшими различиями в зависимости от субъекта федерации

Для большинства субъектов нормы расхождения площади в сторону увеличения после уточнения границ определены следующим образом (в зависимости от целевого назначения земель):

Минимальные размеры устанавливаются региональными и муниципальными нормативными актами с небольшими различиями в зависимости от субъекта федерации. Для большинства субъектов нормы расхождения площади в сторону увеличения после уточнения границ определены следующим образом (в зависимости от целевого назначения земель):

• участки для индивидуального строительства – 300 кв. м;
• участки для дачного строительства – 600 кв. м;
• участки под крестьянские хозяйства – 600 кв. м;
• участки под ЛПХ – 400 кв. м;
• наделы для огородничества (без права строительства) – 400 кв. м;
• земли под гараж – 18 кв. м;
• места под уличную торговлю – 5 кв. м.

Величина допустимых норм расхождения может быть уменьшена до 2-х раз местным законодательством, в зависимости от ситуации в регионе.

Мнение эксперта

Задать вопрос эксперту

Задать вопрос эксперту

Примеры допустимой погрешности

1. Допустимая погрешность измерения времени

Допустимая погрешность при измерении времени может быть различной в зависимости от конкретной задачи или области применения. Например, при измерении продолжительности событий в жизни человека, допустимая погрешность может составлять несколько минут или даже часов. Однако, при научных исследованиях или в индустрии, где требуется высокая точность, допустимая погрешность может быть значительно меньше, до миллисекунд и даже наносекунд.

2. Допустимая погрешность в измерении массы

В области измерения массы величина допустимой погрешности также может различаться. Например, в бытовых условиях допустимая погрешность при взвешивании продуктов может быть около 1 грамма. Однако, в медицине или при выполнении точных измерений в лабораторных условиях, допустимая погрешность может быть значительно меньше, например, до 0,1 миллиграмма или меньше.

3. Допустимая погрешность в измерении длины

Допустимая погрешность в измерении длины также зависит от области применения и требуемой точности. Например, при измерении длины в строительстве или при изготовлении мебели, допустимая погрешность может составлять несколько миллиметров. Однако, в высокоточных машиностроительных операциях или научных исследованиях, допустимая погрешность может быть значительно меньше, до долей микрометра.

4. Допустимая погрешность в измерении температуры

При измерении температуры также существуют стандартные допустимые погрешности. В бытовых условиях допустимая погрешность при использовании термометра может быть около 0,5 градуса Цельсия. В научных исследованиях или промышленности, где требуется высокая точность, допустимая погрешность может быть значительно меньше, до долей градуса или меньше.

5. Допустимая погрешность при измерении электрических величин

В области измерения электрических величин также существуют допустимые погрешности. Например, при измерении напряжения или силы тока в бытовых условиях, допустимая погрешность может быть около 1%. Однако, в промышленности или при научных исследованиях, где требуется высокая точность, допустимая погрешность может быть значительно меньше, до долей процента или меньше.

Примеры допустимой погрешности
Измеряемая величина
Бытовая допустимая погрешность
Высокоточная допустимая погрешность

Время
Несколько минут или часов
До миллисекунд и наносекунд

Масса
Около 1 грамма
До 0,1 миллиграмма или меньше

Длина
Несколько миллиметров
До долей микрометра

Температура
Около 0,5 градуса Цельсия
До долей градуса или меньше

Электрические величины
Около 1%
До долей процента или меньше

Предельная допустимая погрешность

Предельные допустимые погрешности — это гарантированные или максимальные по модулю погрешности, которые возникают при исчерпании допустимых рабочих диапазонов всех величин, вызывающих погрешности. При задании таких погрешностей всегда предполагают отдельное измерение, в то время как для учета статистических составляющих должна быть задана статистическая вероятность, лежащая в их основе.
 

Предельная допустимая погрешность: манометров класса 0 05 при давлениях до 10 % верхнего предела измерения составляет 0 005 % от верхнего предела измерения; манометров класса 0 2 при давлениях до 10 % верхнего — предела1 измерения составляет 0 02 % от верхнего предела измерения.
 

Предельные допустимые погрешности — это гарантированные или максимальные по модулю погрешности, которые возникают при исчерпании допустимых рабочих диапазонов всех величин, вызывающих погрешности. При задании таких погрешностей всегда предполагают отдельное измерение, в то время как для учета статистических составляющих должна быть задана статистическая вероятность, лежащая в их основе.
 

Обоснована предельная допустимая погрешность измерения давления в процессе лабораторной периодической ректификации тяжелых нефтяных остатков при давлениях от 1 33 до 0 0133 кПа ( от 10 до 0 1 мм рт. ст) и температурах от 50 до 330 С, выражающаяся величиной от 1 7 до 3 / 6 от измеряемого давления, что позволяет производить относительную оценку существующих измерителей давления и должно являться нормирующим показателем при разработке новых средств измерения.
 

Обоснована предельная допустимая погрешность измерения давления при лабораторной ректификации тяжелых остатков при давлениях 1 33 кПа — 0 1333 кПа и температурах 50 — 330 С.
 

В этом случае предельные допустимые погрешности будут равны по абсолютной величине половине допуска. Точностью изготовления называется степень приближения действительных значений геометрических и других параметров деталей и изделий к их заданным значениям, указанным в чертежах или технических условиях.
 

При оценке результатов измерений иногда пользуются понятием максимальной или предельной допустимой погрешности, величину которой определяют в долях о или S.
 

При оценке результатов измерений иногда пользуются понятием максимальной или предельной допустимой погрешности, значение которой определяют в долях а или S. А, в которые случайные погрешности должны уложиться.
 

В приложениях № 1, 2, 3 и 4 даны значения предельных допустимых погрешностей различных видов мер и приборов.
 

Ко второй группе относятся величины Ар, р и d, которые могут быть оценены предельной допустимой погрешностью б, зависящей от класса точности измерительных приборов.
 

Для обеспечения единства измерений Госстандартом СССР разработаны поверочные схемы, в которых указаны методы градуировки и поверки приборов, а также их предельные и допустимые погрешности.
 

До выполнения непосредственных испытаний измеряют постоянные величины ( диаметры трубопроводов, положение манометров и др.)) вычисляют постоянные расчетные коэффициенты, оценивают предельную допустимую погрешность. Перед началом испытаний измеряют атмосферное давление и температуру окружающего воздуха.
 

Источниками погрешностей кольцевых дифманомстров являются трение в передаточном механизме прибора, а также неполная компенсация момента от изгиба подводящих трубок. Предельная допустимая погрешность для этих приборов обычно не превышает 1 — 1 5 % от диапазона измерения по шкале. Температурная погрешность практически отсутствует, так как удельный вес затворной жидкости не влияет на показания прибора.
 

Значения рН буферных растворов при температуре 25 С.

Это обеспечивает возможность их работы в комплекте с автоматическими потенциометрами, устройствами регулирования и контроля, использующими унифицированный токовый сигнал. Прибор рН — 201 имеет пять диапазонов измерения числа рН: 1; 2 5; 5; 10; 15, предельная допустимая погрешность составляет 1 % диапазона измерения.
 

Расширенные расчеты

Пусть N будет количеством избирателей в выборке. Предположим, они были отобраны случайным образом и независимо от всего населения

Гипотеза, возможно, слишком сильна, но если составить выборку с осторожностью, реальность может по крайней мере приблизиться к этой ситуации. Пусть p будет долей избирателей в общей численности населения, которые проголосуют «за»

Тогда количество X избирателей в выборке , которые проголосуют «за», является случайной величиной, распределенной в соответствии с биномиальным распределением параметров N и p . Если N достаточно велико, то Х следует нормальному распределение по среднему Np и дисперсия Np (1 — р ). Следовательно

Zзнак равноИкс-НЕТпНЕТп(1-п){\ Displaystyle Z = {\ гидроразрыва {X-Np} {\ sqrt {Np (1-p)}}}}

подчиняется приведенному центрированному нормальному закону (с параметрами 0 и 1).

Таблица нормального распределения показывает , что Р (-2,576 < Z <2,576) = 0,99, или, другими словами, что есть 99 из ста шансов на это событие произойдет. Так,

п(-2,576<ИксНЕТ-пп(1-п)НЕТ<2,576)знак равно,99.{\ displaystyle P \ left (-2,576 <{\ frac {X / Np} {\ sqrt {p (1-p) / N}}} <2,576 \ right) = 0,99.}

Это эквивалентно

п(ИксНЕТ-2,576п(1-п)НЕТ<п<ИксНЕТ+2,576п(1-п)НЕТ )знак равно,99.{\ displaystyle P \ left ({\ frac {X} {N}} — 2,576 {\ sqrt {\ frac {p (1-p)} {N}}} <p <{\ frac {X} {N}) } +2,576 {\ sqrt {\ frac {p (1-p)} {N}}} \ \ right) = 0,99.}

Замена p в первом и третьем членах этого неравенства оценочным значением X / N редко приводит к большим ошибкам, если N достаточно велико. Результатом этой операции являются:

п(ИксНЕТ-2,576(ИксНЕТ)(1-(ИксНЕТ))НЕТ<п<ИксНЕТ+2,576(ИксНЕТ)(1-(ИксНЕТ))НЕТ )знак равно,99.{\ displaystyle P \ left ({\ frac {X} {N}} — 2,576 {\ sqrt {\ frac {(X / N) (1- (X / N))} {N}}} <p <{ \ frac {X} {N}} + 2,576 {\ sqrt {\ frac {(X / N) (1- (X / N))} {N}}} \ \ right) = 0,99.}

Первый и третий члены неравенства зависят от наблюдаемого значения X / N и ненаблюдаемого значения p и являются крайними значениями доверительного интервала. Другими словами, погрешность составляет

2,576(ИксНЕТ)(1-(ИксНЕТ))НЕТ.{\ displaystyle 2,576 {\ sqrt {\ frac {(X / N) (1- (X / N))} {N}}}.}

Количественная информация

При количественном определении неопределенностей и пределов погрешности следует учитывать качество информации.

Пример : заявление «5%» должно содержать оценку и заменять «около 5%»; В этом контексте цифра «5» никогда не бывает математически точной, поэтому к ней можно добавить любое количество нулей после запятой. Показатель «4,8%» вряд ли свидетельствует о повышенном внимании.

Никакие «точные» результаты не могут быть получены из «грубого» начального положения, потому что в результате действуют правила распространения ошибок пределов ошибок для взаимно независимых значений (см. Ниже: Расчет с пределами ошибок):

Результат никогда не может быть более точным, чем то, что в него вложено. (Исключение составляют случайные ошибки: здесь после повторных измерений среднее значение становится более точным, чем отдельное измеренное значение).

Пример : 5% 15,6 В = 0,8 В, а не 0,78 В,

если 5,0% не могут заявить об ответственности.

Это требование соответствует требованию в DIN 1333 : Погрешности приведены с более значащей цифрой, для чисел 1 или 2, причем в этом случае две , за исключением значащих цифр даны.

Пример : 5% 35,6 В = 1,8 В, а не 2 В.

Начальный ноль не имеет значения.

Пример : спецификация 0,8 В содержит только одну значащую цифру.

Частью концепции предельного значения является то, что оно может быть округлено только в большую сторону, а не в меньшую; то же самое относится и к погрешности согласно DIN 1333. Фактически, предел погрешности 5% · 6,2 В = 0,31 В должен быть округлен до 0,4 В, а не до 0,3 В; но здесь следует быть осторожным, потому что уже 4,8% · 6,2 В <0,3 В.

Нет ничего плохого в том, чтобы вычислить более точно на промежуточных этапах, чтобы ошибки округления не накапливались, и только для учета пределов ошибок при достижении результата, см. Также .

Информацию и примеры по пределам погрешности измерительного устройства можно найти

• для аналоговых электроизмерительных приборов с классом точности согласно DIN EN 60051,
• для цифровых электроизмерительных приборов под цифровым мультиметром , погрешность измерительного прибора .

Определение содержания микроэлементов и тяжелых металлов в растениях, оценка безопасности льнопродукции методом атомно-эмиссионной спектрометрии с индуктивно связанной плазмой

Во Всероссийском научно-исследовательском институте агрохимии изучали возможность использования метода атомноэмиссионной спектрометрии с индуктивно связанной плазмой, в сочетании с микроволновой минерализацией в качестве пробоподготовки, для определения содержания микроэлементов и тяжелых металлов в растениях и продукции растениеводства. Cодержание тяжелых металлов и микроэлементов (кадмия, свинца, меди, цинка) определяли в пробах льносемян и льноволокна, выращенных в абсолютном контроле в опыте РГАУ–МСХА им. К.А. Тимирязева. Первоочередное значение имела метрологическая характеристика предлагаемого подхода. Величина доверительного интервала (α = 0,05) была ниже 10 %. Для цинка и свинца это находится на уровне погрешности измерения стандартизированным методом (атомно-абсорбционная спектроскопия) после классического озоления, а для меди и кадмия даже ниже. В целом содержание тяжелых металлов в льносеменах не превышало значений предельно допустимых концентраций, установленных Евразийс…

Средняя квадратическая ошибка

_______Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

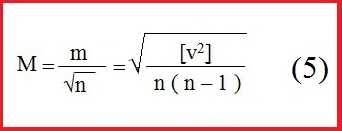_______Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

_______Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки.
___

_______Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность
измерения линии длиной:

_______l = 110 м, при m = 2 см, равна m/l = 1/5500.

_______Пример:

_______Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1

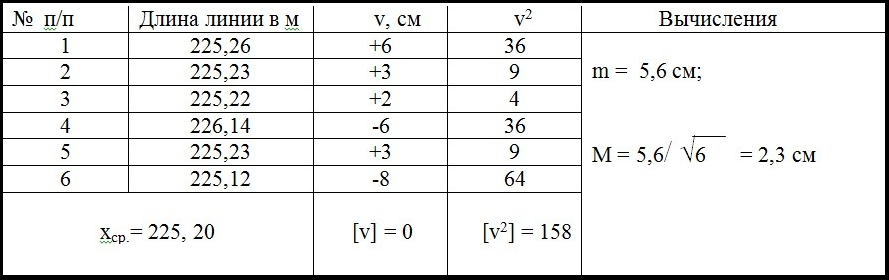_______По формулам вычислены абсолютные средние квадратические ошибки, а оценивать
точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная
ошибка вероятнейшего значения измеренной линии равна

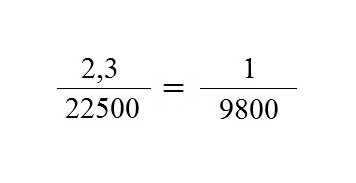Примеры предельной погрешности

Предельная погрешность – это ошибка, которая возникает при проведении измерений или вычислений и характеризует максимальное отклонение полученного значения от истинного значения величины. Рассмотрим некоторые примеры предельной погрешности.

1. Пример 1: Измерение длины провода

   Предположим, что необходимо измерить длину провода с помощью линейки длиной 30 см. Однако, при этом использование линейки с миллиметровыми делениями ведет к неопределенности в определении наиболее близких значений. Таким образом, предельная погрешность измерения длины провода может составлять +/-1 мм.

2. Пример 2: Вычисление площади треугольника

   Предположим, что необходимо вычислить площадь треугольника с помощью формулы S = 1/2 * a * h, где a — основание треугольника, h — высота треугольника. Если значения основания и высоты измерены с погрешностью, то итоговая предельная погрешность расчета площади будет зависеть от предельной погрешности измерений основания и высоты.

3. Пример 3: Измерение времени реакции

   Предположим, что необходимо измерить время реакции человека на внешний стимул. В данном случае предельная погрешность измерения будет зависеть от точности использованного прибора, такого как секундомер, а также от субъективных факторов, например, от времени отклика оператора при нажатии кнопки остановки секундомера.

Это лишь некоторые примеры предельной погрешности, которая может возникать при измерениях и вычислениях

Важно учитывать предельную погрешность, чтобы получить более точные результаты и избежать неверных интерпретаций данных

Как учитывать допустимую погрешность: рекомендации и методы

Допустимая погрешность играет важную роль во многих областях науки, техники и измерений. Ее учет позволяет определить допустимые отклонения и границы ошибок в проводимых измерениях и расчетах. В этом разделе мы рассмотрим рекомендации и методы по учету допустимой погрешности.

1. Определение допустимой погрешности.

Первым шагом в учете допустимой погрешности является определение самой погрешности. Она может быть указана в виде абсолютного значения или процентного отношения к измеряемой величине. Например, допустимая погрешность измерения длины может быть равной +/- 0.1 мм или 1% от измеряемой длины.

2. Учет систематической и случайной погрешностей.

При учете допустимой погрешности необходимо различать систематическую и случайную погрешности. Систематическая погрешность возникает из-за постоянных ошибок в измерительной системе и может быть скорректирована путем калибровки или использования исправленных значений. Случайная погрешность связана с непредсказуемыми факторами, такими как шумы или флуктуации, и может быть учтена с помощью статистических методов, например, усреднения значений или использования доверительных интервалов.

3. Использование стандартных значений.

В некоторых случаях, для учета допустимой погрешности могут быть использованы стандартные значения, предоставленные производителем или установленные отраслевыми стандартами. Например, в измерениях электрических сопротивлений может быть использован стандартный набор значений с определенными допустимыми отклонениями.

4. Обеспечение качества измерений.

Для более точных измерений и учета допустимой погрешности рекомендуется следовать методам обеспечения качества. Это может включать калибровку инструментов, использование высокоточных измерительных приборов, повторное измерение и проверку результатов с использованием независимых методов.

5. Документирование и контроль.

Наконец, для правильного учета допустимой погрешности необходимо документировать все проводимые измерения и контролировать процесс измерений. Это позволяет отслеживать возможные источники погрешностей, принимать соответствующие корректировки и обеспечивать повторяемость результатов.

Следуя рекомендациям по учету допустимой погрешности и используя соответствующие методы, можно получить более точные и надежные результаты измерений

Это особенно важно в областях, где точность и надежность данных имеют решающее значение, например в физике, биологии, инженерии и производстве

Допуск

На производстве используют понятие допуск, устанавливая верхнее и нижнее значение, в пределах которых
измеряемый объект не считается браком. Например, при производстве конденсаторов ёмкостью 100±5% мкФ
устанавливается допуск 5%, это означает, что на этапе контроля качества при замере ёмкости конденсатора,
конденсаторы ёмкостью более 105 мкФ и менее 95 мкФ считаются браком.

При контроле качества необходимо учитывать неопределённость измерительного инструмента, так, если
неопределённость измерения ёмкости конденсатора составляет 2 мкФ, то результат измерения 95 мкФ может
означать 93-97 мкФ. Для учёта неопределённости в результатах измерений необходимо расширить
понятие допуска: в допуске должна быть учтена неопределённость измерительного прибора. Для этого необходимо
задать доверительный интервал, т.е. процент деталей, который должен гарантированно соответствовать заданным
параметрам.

Доверительный интервал строится по нормальному распределению: считается, что результат измерения
соответствует нормальному распределению
μ±kσ. Вероятность нахождения значения в пределах ku зависит от значения k:
при k=1 68,3% измерений попадут в значение σ±u, при k=3 — 99,7%.

Области применения

Научные исследования. В научных исследованиях часто требуется проведение измерений и оценка погрешностей. Предел допускаемой погрешности позволяет определить, насколько точные результаты можно считать достоверными и учесть возможное влияние случайных факторов на полученные данные.
Изготовление и контроль качества продукции. В процессе производства различных товаров и изделий необходимо учитывать предельно допустимую погрешность, чтобы гарантировать качество и соответствие продукции установленным стандартам. Например, при изготовлении механических деталей допустимое отклонение размеров может быть оговорено в техническом задании.
Финансовые расчеты и анализ данных

В финансовой сфере точность расчетов имеет особую важность. Предел допускаемой погрешности позволяет оценить, насколько точный и достоверный является финансовый отчет или аналитические данные, и принять взвешенные финансовые решения.
Медицинские исследования и диагностика

В медицине точность измерений и полученных данных имеет решающее значение для определения диагноза, назначения лечения и прогноза исхода заболевания. Применение понятия предела допускаемой погрешности позволяет контролировать достоверность результатов и предоставить пациенту наиболее точную и объективную информацию.
Экспертиза и судебное разбирательство. В юриспруденции и экспертных исследованиях понятие предела допускаемой погрешности может быть востребовано при проведении экспертиз, определении виновности и возмещении ущерба. Например, при рассмотрении технической неисправности автомобиля можно использовать предельно допустимую погрешность при оценке причин аварии.