Метод координат

Ордината и ее значение в математике

Ордината — это одна из координат в прямоугольной системе координат, которая отображает положение точки на графике по вертикали. Она определяется расстоянием от точки до оси абсцисс.

Значение ординаты задается числом и может быть положительным или отрицательным, в зависимости от положения точки относительно оси абсцисс. Положительное значение ординаты означает, что точка находится выше оси абсцисс, а отрицательное значение — что точка находится ниже оси абсцисс.

Ордината играет важную роль в математике, особенно при построении графиков функций. Она позволяет определить положение точки на плоскости и отобразить ее в пространстве координат. Также ордината используется для измерения вертикального расстояния между точками и осью абсцисс.

Для удобства работы с ординатой и ее значением, довольно часто используются числовые оси с отметками. На оси ординат обычно указываются значения, которые соответствуют позициям точек на графике. Это помогает быстро определить положение точек и анализировать их значения.

Ордината также часто используется для вычисления и построения графиков различных математических функций. Значения ординаты меняются в зависимости от значений аргумента функции, что позволяет представить ее зависимость от других переменных и анализировать ее поведение на графике.

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам, например, точки D (−4 , 2), надо:

1. Отметить на оси «Ox», точку с координатой
   «−4», и провести через неё прямую перпендикулярную оси «Ox».
2. Отметить на оси «Oy»,
   точку с координатой 2, и провести через неё прямую перпендикулярную
   оси «Oy».

3. Точка пересечения перпендикуляров (·) D — искомая точка.
   У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

1. Сместиться по оси «x» влево на4 единицы, так как у нас перед 4
   стоит «−».
2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так
   как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Latitude and longitude[edit]

Diagram of the latitude ϕ and longitude λ angle measurements for a spherical model of the Earth.

The «latitude» (abbreviation: Lat., ϕ, or phi) of a point on Earth’s surface is the angle between the equatorial plane and the straight line that passes through that point and through (or close to) the center of the Earth. Lines joining points of the same latitude trace circles on the surface of Earth called parallels, as they are parallel to the Equator and to each other. The North Pole is 90° N; the South Pole is 90° S. The 0° parallel of latitude is designated the Equator, the fundamental plane of all geographic coordinate systems. The Equator divides the globe into Northern and Southern Hemispheres.

The «longitude» (abbreviation: Long., λ, or lambda) of a point on Earth’s surface is the angle east or west of a reference meridian to another meridian that passes through that point. All meridians are halves of great ellipses (often called great circles), which converge at the North and South Poles. The meridian of the British Royal Observatory in Greenwich, in southeast London, England, is the international prime meridian, although some organizations—such as the French Institut national de l’information géographique et forestière—continue to use other meridians for internal purposes. The prime meridian determines the proper Eastern and Western Hemispheres, although maps often divide these hemispheres further west in order to keep the Old World on a single side. The antipodal meridian of Greenwich is both 180°W and 180°E. This is not to be conflated with the International Date Line, which diverges from it in several places for political and convenience reasons, including between far eastern Russia and the far western Aleutian Islands.

The combination of these two components specifies the position of any location on the surface of Earth, without consideration of altitude or depth. The visual grid on a map formed by lines of latitude and longitude is known as a graticule. The origin/zero point of this system is located in the Gulf of Guinea about 625 km (390 mi) south of Tema, Ghana, a location often facetiously called Null Island.

Применение абсциссы и ординаты в науке и технике

В математике абсцисса и ордината используются для построения координатной системы. Координатная система представляет собой двумерное пространство, где каждая точка имеет свои уникальные значения абсциссы и ординаты. Это позволяет представить графики функций, изучать их свойства и решать уравнения.

В геометрии абсциссы и ординаты используются для определения положения точек в пространстве. Например, при работе с координатами геометрических фигур, можно определить их расположение, размеры и форму. Данная информация существенна при разработке проектов в архитектуре, дизайне и строительстве.

Физика использует абсциссы и ординаты для описания движения и взаимодействия объектов в пространстве. Координаты точек позволяют вычислить скорость, ускорение и другие физические характеристики объектов. Это особенно полезно при моделировании и симуляции различных процессов и явлений.

В инженерии и технике абсциссы и ординаты используются для определения местоположения и перемещения объектов. Например, GPS-навигация опирается на координаты, чтобы рассчитать путь и определить точное положение. Координаты также являются важными при разработке автоматизированных систем и робототехнике.

В информатике абсцисса и ордината используются для организации и хранения данных в двумерных массивах. Координаты значений образуют структуру, которая позволяет эффективно обрабатывать, анализировать и отображать информацию. Координаты также применяются в различных алгоритмах для поиска, сортировки и обработки данных.

Таким образом, абсциссы и ординаты играют важнейшую роль в науке и технике, предоставляя способ установления и измерения положения точек в пространстве. Благодаря этим координатам мы можем лучше понимать и взаимодействовать с окружающим миром, а также разрабатывать новые технологии и улучшать существующие системы.

Понятие и примеры абсциссы и ординаты

Абсцисса — это горизонтальная координата точки, обозначенная символом х. Она измеряется относительно оси Х, которая пересекает плоскость в нулевой точке (0,0). Если точка находится левее оси Х, то абсцисса будет отрицательной, а если точка находится правее — абсцисса будет положительной.

Ордината — это вертикальная координата точки, обозначенная символом y. Она измеряется относительно оси Y, которая также пересекает плоскость в нулевой точке (0,0). Если точка находится ниже оси Y, то ордината будет отрицательной, а если точка находится выше — ордината будет положительной.

Пример:

Рассмотрим точку A с координатами (3,5). Здесь число 3 — это абсцисса точки A, а число 5 — ордината.

То есть, точка A находится на расстоянии 3 от оси X и 5 от оси Y.

Шаг 2: Установка начала координат

Чтобы установить начало координат, необходимо определить точку на плоскости, в которой обе координаты равны нулю. Обычно начало координат обозначается буквой O или 0.

Затем, с помощью линейки или другого измерительного инструмента, нужно провести прямые оси, проходящие через точку O. Горизонтальная ось будет представлять абсциссу, а вертикальная — ординату. Ориентация этих осей может быть разной, в зависимости от выбранной системы координат и задачи.

Установка начала координат является важным шагом при работе с графиками и построении различных математических моделей.

Шаг 2.1: Отметка начала оси абсцисс

Как найти начало оси абсцисс на графике? Для этого необходимо определить точку, где ось абсцисс пересекает ось ординат. Начало оси абсцисс обычно обозначается буквой O. Эта точка имеет координаты (0, 0), так как она расположена на пересечении этих двух осей.

Шаг 2.2: Отметка начала оси ординат

Чтобы найти начало оси ординат, необходимо определить точку, в которой она пересекает ось абсцисс. Для этого следует найти на графике местоположение точки, где график пересекает ось абсцисс.

Сначала находим точку, в которой график пересекает ось абсцисс. Это точка, в которой значение оси абсцисс равно нулю. Мы можем определить это значение, исследуя график и отмечая пересечение с осью абсцисс.

Укажем эту точку на графике, отметив ее символом «О». Это будет начало оси ординат. Теперь у нас есть точка, определяющая начало оси ординат.

Координаты на плоскости

Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.

Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью.

Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые, на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.

Определение 1

Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.

Две перпендикулярные оси х и у с делениями составляют прямоугольную, или декартовую, систему координат, которую предложил французский философ и математик Рене Декарт.

Координатная плоскость

Координаты точки

Точка на координатной плоскости определяется двумя координатами.

• Курсовая работа 480 руб.
• Реферат 270 руб.
• Контрольная работа 250 руб.

Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.

Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.

Для нанесения точки на координатную плоскость действуют в обратном порядке.

Построение точки по заданным координатам

Пример 1

На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$

Решение.

Построение точки $A$:

• отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
• на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.

Построение точки $B$:

• отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
• на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.

Пример 2

Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.

Решение.

Построение точки $C$:

• отложим число $3$ на оси $x$;
• координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.

Построение точки $D$:

• отложим число $2$ на оси $y$;
• координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.

Замечание 1

Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.

Пример 3

Определить координаты точек A, B, C, D.$

Решение.

Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$

Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$

Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$

Пример 4

Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$

Решение.

Построение точки $E$:

• отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
• на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
• на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$

Построение точки $F$:

• координата $y=0$, значит, точка лежит на оси $x$;
• отложим на оси $x$ число $5$ и получим точку $F(5; 0).$

Построение точки $G$:

• отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
• на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
• на пересечении перпендикулярных прямых получаем точку $G(3; 4).$

Построение точки $H$:

• координата $x=0$, значит, точка лежит на оси $y$;
• отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$

Построение точки $O$:

обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).

Координатная ось — «фотография» чисел в виде точек на прямой ##

пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.

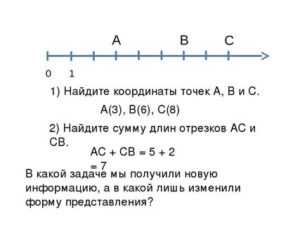
Чтобы из любой прямой получить координатную ось ,необходимо выбрать на ней нулевую точку$0$- это будет началом отсчета ;отметитьточку$1$ — определить единичный отрезок(т.е. выбрать масштаб)инарисовать стрелочку в положительном направлении отсчёта .На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу$3$на координатной прямойсопоставляется единственная точка$A$, точке$B$-единственное число$-2$, такое число назвали координатой.

Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.

пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.

Координаты точек на прямой.

пробa Точка$O$разбиваетпрямую$AB$на два луча$OA$и$OB$ . Если примем точку$O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось .Рассмотрим на ней произвольную точку .Как определить ее положение?Для ответа на этот вопрос придумали понятие — координата . Положение любой точки на координатной осизадается её координатой.Чтобы отличить друг от друга координаты , перед числами на левом луче$OA$условились ставить знак «минус », а перед числами на правом луче$OB$-знак«плюс».

Координатысо знаком»$-$»называются отрицательными.Координатысо знаком «+» называютсяположительными .

Точка$O$- начало отсчета илиначало координат , изображает ноль.Само число$0$не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .

Координата точки — это число , показывающее положение точки на прямой.

Записывают координаты точек$B$,$C$,$D$следующим образом:$B(-4,2)$,$C\left(-\frac{1}{2}\right)$,$D(3,9)$.

Изображение чисел точками на координатной оси.

Числа на координатной прямой выглядят точками. Для тогочтобыпостроитьточку, соответствующую некоторому числу$a$ , нужно:определить знак этого числа ;от начала координат отложить отрезок , равный$\left|a\right|$вправо , если знак»+»ивлево , еслизнак»-» .

Число$a$в таком случае называют координатой построенной точки .

На рисунке числа $3$, $\frac{1}{4}$,$-0,9$изображены соответсвенно точками$B$,$C$,$D$. Числа- это«адреса»точек на координатной прямой.Точки-это»фотографии» чисел.

Введение оси координат:
1) Выбрать на прямой начало координат;
2) Выбрать положительное направление;
3) Выбрать единичный отрезок.

Координаты точки:
Каждой точке можно присвоить свою координату-это расстояние от точки до начала координат с учетом знака: слева от $0$знак $-$ , справа$+$.

Изображение числа : пробa
По любой координате можно восстановить точку.

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

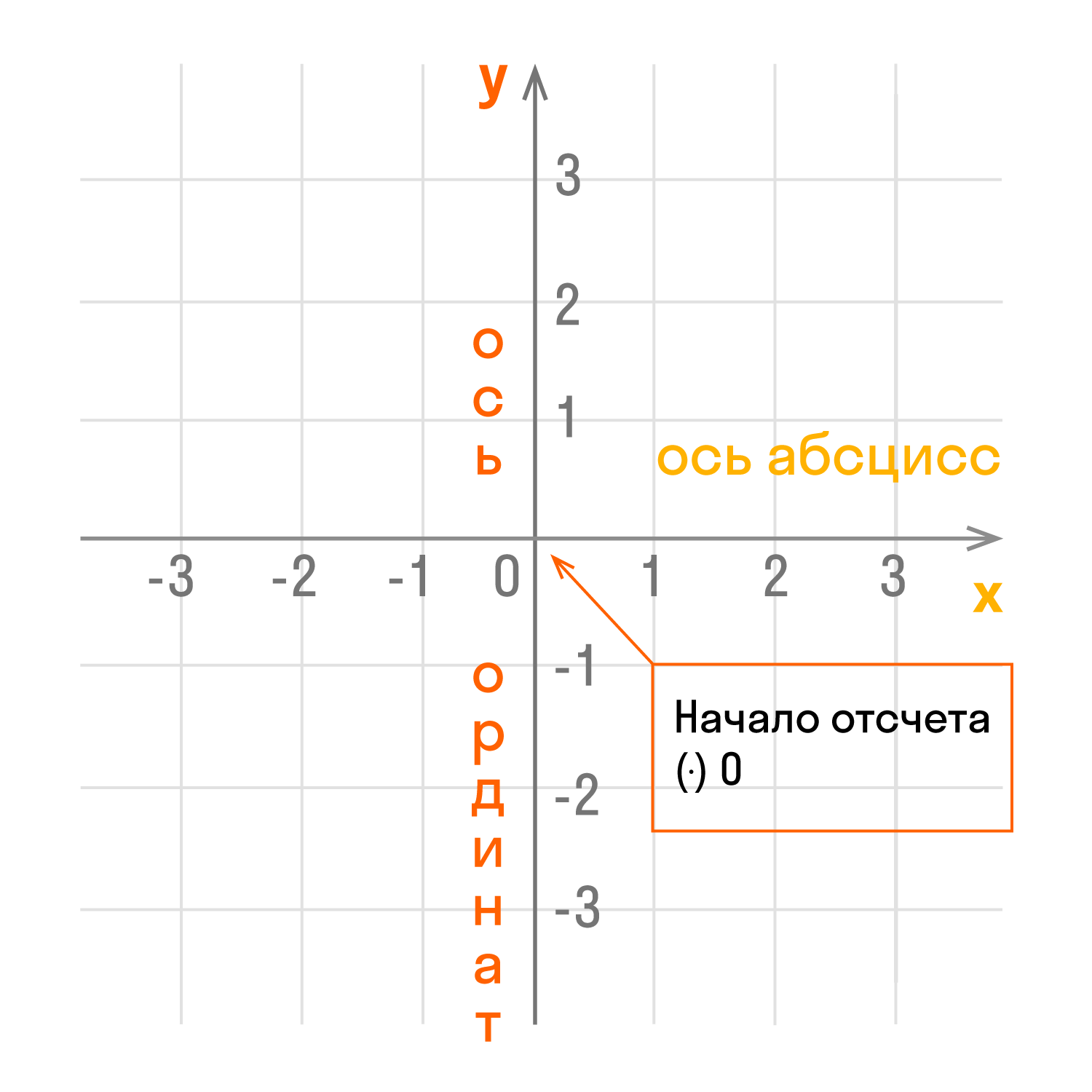
• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

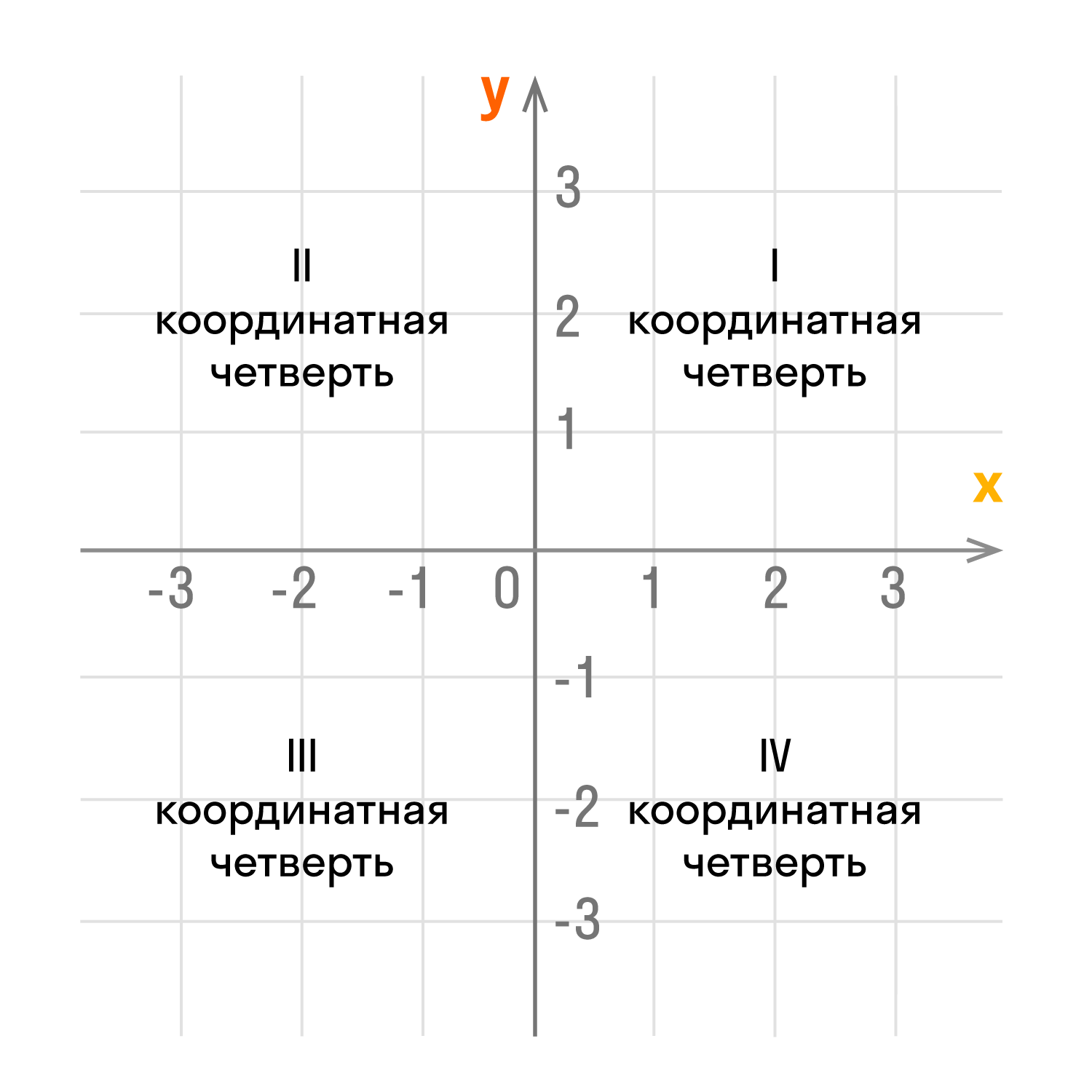
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

Правила координат:

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Шаг 3: Определение точки на координатной плоскости

После того, как мы нашли значение абсциссы и ординаты по отдельности, настало время определить точку на координатной плоскости.

Чтобы найти точку, соединяем найденные значения абсциссы и ординаты на плоскости с помощью линии. Найденная точка будет точкой пересечения этой линии с координатной плоскостью.

Координатная плоскость представляет собой двумерную систему, где горизонтальная ось называется осью абсцисс, а вертикальная ось — осью ординат. Она помогает нам визуализировать и определять точки в пространстве.

Таким образом, путем соединения найденных значений абсциссы и ординаты, мы сможем определить точку на координатной плоскости и использовать ее для решения различных математических задач.

Шаг 3.2: Определение ординаты точки

1. Изучите задачу и позицию точки на координатной плоскости.
2. Определите на оси ординат масштаб и выберите единицы измерения, если это необходимо.
3. Отметьте точку на оси ординат в соответствии с её координатой.
4. Запишите значение ординаты точки.

Применяя эти шаги, вы сможете точно определить ординату точки и использовать её в дальнейших расчетах.

Простая формула для нахождения абсциссы точки по заданной ординате

Когда нам задают ординату точки на плоскости, абсциссу этой точки можно найти следующим образом:

1. Определите положение точки на плоскости. Для этого учтите знак ординаты, отрицательная ордината будет находиться под осью X, а положительная — над осью X.
2. Установите соответствующий знак для абсциссы точки. Если ордината отрицательная, абсцисса будет иметь отрицательное значение, и наоборот.
3. Известно, что точка лежит на плоскости. Если ордината точки равна 0, то абсцисса будет равна 0, так как точка будет находиться на оси X.
4. Если ордината точки не равна 0, воспользуйтесь формулой для нахождения абсциссы точки. Для этого разделите ординату на тангенс угла наклона прямой, проходящей через начало координат и точку.

Теперь, зная значение ординаты и применяя простую формулу, вы можете легко определить абсциссу точки на плоскости. Этот метод является универсальным и применим в различных задачах, связанных с геометрией

Обратите внимание на особые случаи, которые могут возникнуть при нахождении абсциссы точки и всегда проверяйте полученные результаты

Как найти абсциссу точки на координатной плоскости?

Чтобы найти абсциссу точки на координатной плоскости, нужно проанализировать ее расположение относительно осей и посмотреть на соответствующие значения координат.

Представим, что у нас есть точка на плоскости с координатами (x, y). Абсцисса этой точки будет x.

Если точка находится на положительной стороне оси ординат, абсцисса будет положительной. Если точка находится на отрицательной стороне оси ординат, абсцисса будет отрицательной.

Чтобы найти абсциссу точки, можно использовать следующие шаги:

1. Найдите точку на координатной плоскости.
2. Определите расположение точки относительно осей.
3. Определите значение координаты x точки.

Например, рассмотрим точку A с координатами (-3, 2). В данном случае значение x равно -3.

Теперь вы знаете, как найти абсциссу точки на координатной плоскости! Используйте эти шаги для определения абсциссы любой точки.

Декартова система координат.

Фиксируем в пространстве точку \(O\) и рассмотрим произвольную точку \(M\). Радиус-вектором точки \(M\) по отношению к точке \(O\) называется вектор \(\overrightarrow{OM}\). Если в пространстве кроме точки \(O\) выбран некоторый , то точке \(M\) сопоставляется упорядоченная тройка чисел — компоненты ее радиус-вектора.

Определение.

Декартовой системой координат в пространстве называется совокупность точки и базиса.

Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат; первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Определение.

Пусть дана декартова система координат \(O\), \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\). Компоненты \(x\), \(y\), \(z\) радиус-вектора \(\overrightarrow{OM}\) точки \(M\) называются координатами точки \(M\) в данной системе координат:
$$
\overrightarrow{OM} = x\boldsymbol{e_{1}} + y\boldsymbol{e_{2}} + z\boldsymbol{e_{3}}.\nonumber
$$
Первая координата называется абсциссой, вторая — ординатой, а третья — аппликатой.

Аналогично определяются координаты на плоскости и на прямой линии. Разумеется, точка на плоскости имеет только две координаты, а на прямой линии — одну.

Координаты точки пишут в скобках после буквы, обозначающей точку. Например, запись \(A(2,\ 1/2)\) означает, что точка \(A\) имеет координаты 2 и 1/2 в ранее выбранной декартовой системе координат на плоскости (рис. 2.1).

Рис. 2.1

Координаты точки, как и компоненты вектора, — величины безразмерные. В частности, они не зависят от выбранной единицы измерения длин. В самом деле, раскладывая векторы в теореме о , мы сводили дело к разложению вектора по коллинеарному с ним ненулевому вектору. А в этом случае компонента равна .
Легко видеть, что при заданной системе координат координаты точки определены однозначно. С другой стороны, если задана система координат, то для каждой упорядоченной тройки чисел найдется единственная точка, имеющая эти числа в качестве координат. Система координат на плоскости определяет такое же соответствие между точками плоскости и парами чисел. Задание системы координат на прямой линии сопоставляет каждой точке вещественное число и каждому числу — точку.

Рис. 2.2

Рассмотрим две точки \(A\) и \(B\), координаты которых относительно некоторой декартовой системы координат \(O\), \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) соответственно \(x_{1}\), \(y_{1}\), \(z_{1}\) и \(x_{2}\), \(y_{2}\), \(z_{2}\). Поставим себе задачу найти компоненты вектора \(\overrightarrow{AB}\). Очевидно, что \(\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA}\) (рис. 2.2). Компоненты радиус-векторов \(\overrightarrow{OA}\) и \(\overrightarrow{OB}\) равны (\(x_{1}\), \(y_{1}\), \(z_{1}\)) и (\(x_{2}\), \(y_{2}\), \(z_{2}\)) по определению координат. Из ранее доказанного следует, что \(\overrightarrow{AB}\) имеет компоненты (\(x_{2}-x_{1}\), \(y_{2}-y_{1}\), \(z_{2}-z_{1}\)). Этим доказано следующее утверждение.

Утверждение 1.

Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.

History[edit]

The invention of a geographic coordinate system is generally credited to Eratosthenes of Cyrene, who composed his now-lost Geography at the Library of Alexandria in the 3rd century BC. A century later, Hipparchus of Nicaea improved on this system by determining latitude from stellar measurements rather than solar altitude and determining longitude by timings of lunar eclipses, rather than dead reckoning. In the 1st or 2nd century, Marinus of Tyre compiled an extensive gazetteer and mathematically plotted world map using coordinates measured east from a prime meridian at the westernmost known land, designated the Fortunate Isles, off the coast of western Africa around the Canary or Cape Verde Islands, and measured north or south of the island of Rhodes off Asia Minor. Ptolemy credited him with the full adoption of longitude and latitude, rather than measuring latitude in terms of the length of the midsummer day.

Ptolemy’s 2nd-century Geography used the same prime meridian but measured latitude from the Equator instead. After their work was translated into Arabic in the 9th century, Al-Khwārizmī’s Book of the Description of the Earth corrected Marinus’ and Ptolemy’s errors regarding the length of the Mediterranean Sea, causing medieval Arabic cartography to use a prime meridian around 10° east of Ptolemy’s line. Mathematical cartography resumed in Europe following Maximus Planudes’ recovery of Ptolemy’s text a little before 1300; the text was translated into Latin at Florence by Jacobus Angelus around 1407.

In 1884, the United States hosted the International Meridian Conference, attended by representatives from twenty-five nations. Twenty-two of them agreed to adopt the longitude of the Royal Observatory in Greenwich, England as the zero-reference line. The Dominican Republic voted against the motion, while France and Brazil abstained. France adopted Greenwich Mean Time in place of local determinations by the Paris Observatory in 1911.

Координаты точки

Точка на координатной плоскости определяется двумя координатами.

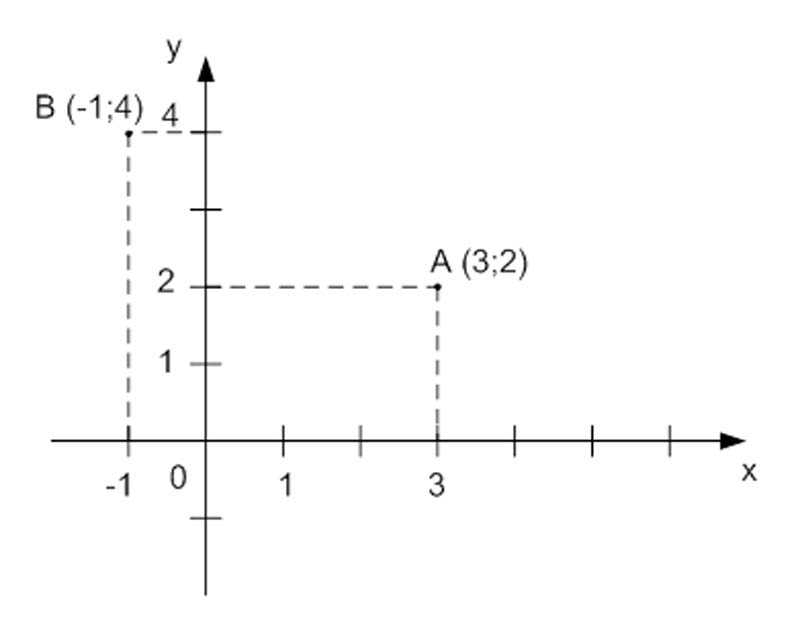
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.

Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.

Для нанесения точки на координатную плоскость действуют в обратном порядке.