Прямоугольная система координат

Основные принципы системы координат в физике 9 класс

Система координат — это метод обозначения и измерения положения точек в пространстве. В физике 9 класс используется прямоугольная декартова система координат, которая состоит из двух осей — горизонтальной (ось OX) и вертикальной (ось OY).

Основные принципы системы координат в физике 9 класс:

• Начало координат. В прямоугольной системе координат начало координат обозначается точкой O, которая совпадает с пересечением осей OX и OY.
• Направление осей. Ось OX направлена горизонтально вправо, а ось OY направлена вертикально вверх.
• Единицы измерения. Для измерения расстояний на осях используются одинаковые единицы измерения, которые могут быть выбраны в соответствии с конкретной задачей.
• Положительные и отрицательные координаты. На оси OX положительные координаты отсчитываются вправо от начала координат, а отрицательные — влево. На оси OY положительные координаты отсчитываются вверх от начала координат, а отрицательные — вниз.
• Координаты точек. Любая точка в системе координат задается двумя числами — ее координатами (x; y), где x — горизонтальная координата (абсцисса), а y — вертикальная координата (ордината).

Система координат играет важную роль в физике, так как позволяет определить положение и перемещение объектов в пространстве. Она также используется для описания физических явлений, построения графиков и анализа данных в различных задачах.

Понятие декартовой системы координат

Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния нужно пройти строго вперёд, а затем — строго вправо, чтобы оказаться в некоторой другой точке, то вы уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой координат в пространстве.

Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат .

С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.

Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.

С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x — a)² + (y — b)² = R² .

Изменение вертикальной подписи

Чтобы изменить вертикальную подпись, кликаем по кнопке «Оси», и далее переходим по наименованию «Основная вертикальная ось». Как видим, в данном случае, нам представляется больше вариантов выбора размещения подписи на оси. Можно вообще не показывать ось, а можно выбрать один из четырех вариантов отображения чисел:

• в тысячах;
• в миллионах;
• в миллиардах;
• в виде логарифмической шкалы.

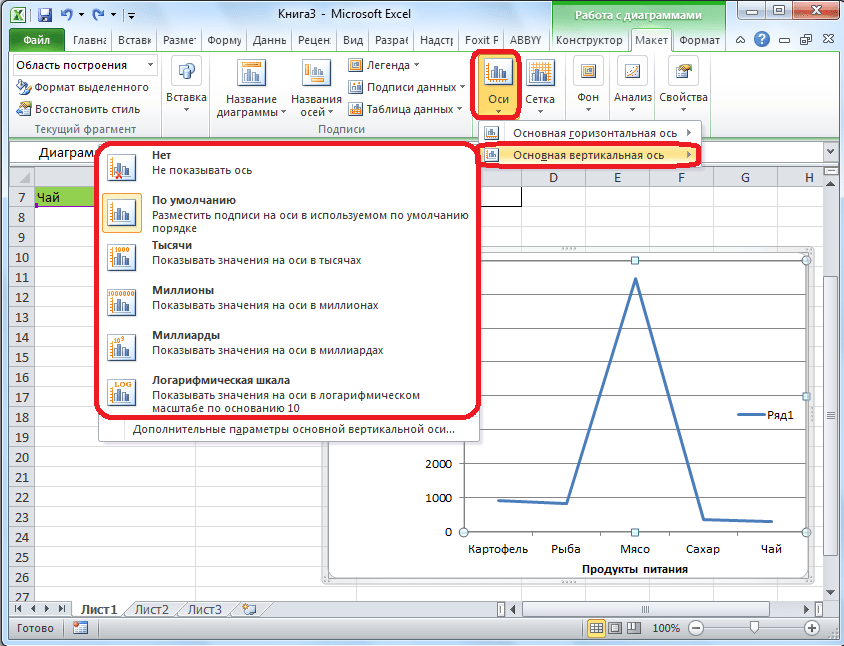
Как нам демонстрирует график ниже, после выбора конкретного пункта, соответственно изменяются и значения шкалы.

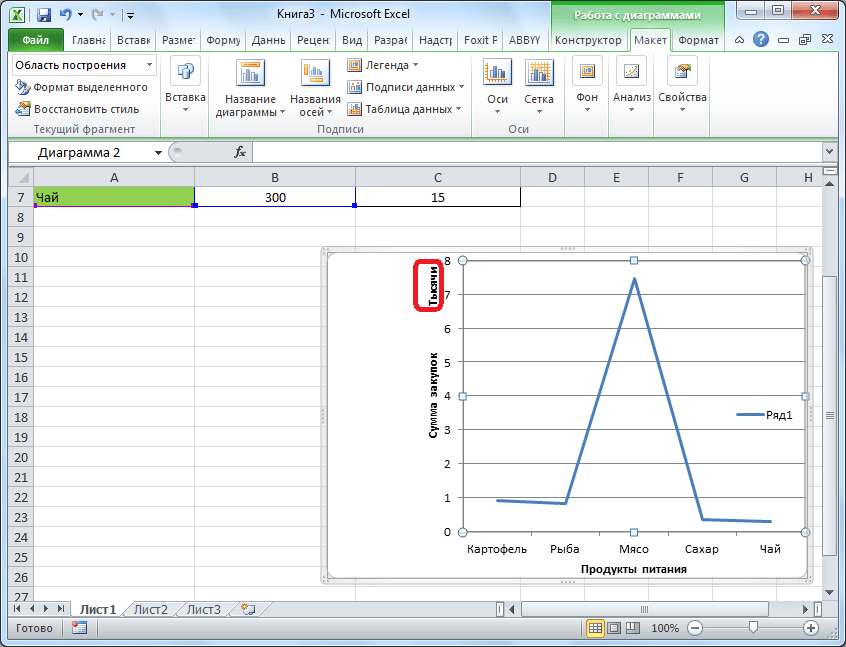
Кроме того, тут же можно выбрать «Дополнительные параметры основной вертикальной оси…». Они аналогичны соответствующему пункту для горизонтальной оси.

Как видим, включение наименования и подписи осей в программе Microsoft Excel процесс не особенно сложный, и, в целом, интуитивно понятный. Но, все-таки с ним легче разобраться, имея под рукой подробное руководство действий. Таким образом, можно значительно сэкономить время на изучении данных возможностей.

Помогла ли Вам статья?

Нет

Абсолютная величина действительного числа

Определение:

Абсолютной величиной или модулем действительного числа х называется само это число, если х ≥ 0 и число -х, если х < 0:(2.1)

Например: |2| = 2, т. к. 2 > 0, |- 3| = -(-3) = 3, т. к. — 3 < 0,∣x² + 4| = x² + 4, т. к. x² + 4 > О при всех х ∈ R, |0| = 0.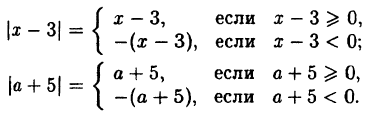

Модуль дейcтвительного числа х равен расстоянию на числовой оси от точки х до начала координат.

Расстояние между двумя точками на оси с координатами x₁ и х₂ выражается формулой:(2.2) d = ∣x₂ — x₁∣

Докажем эту формулу для случая, когда х₂ ≥ x₁ ≥ 0 (рис. 15)

В этом случаеOM₁ = x₁ , OM₂ = x₂ и d — M₁M₂ = OM₂ — OM₁ — x₂ — x₁ — ∣ x₂ — x₁ ∣.Если x₁>x₂ ≥ 0 (рис. 15), то d = M₁M₂ = OM₂ — OM₁ — x₁ — х₂ — (x₂ — x₁) = ∣х₂ — x₁∣ , т. к. х₂ — x₁ < 0.

Рис. 15. Расстояние между точками на оси

Для остальных случаев расположения M₁ и M₂ формула доказывается аналогично.

Пример:

Для данных а и R > 0 отметить на числовой оси множество M = {x|| x — а |< R}.

Решение:

В соответствии с формулой 2.2 множество M есть множество точек числовой оси, расстояние от которых до данной точки меньше R, т.е. интервал с центром в а и длиной 2R: M = {x||x — α |< R} = {x|x ∈ (а — R; а + R)} = = {x∣α — R < х < а + R}.

Ответ: см. рис. 16.

Рис. 16. {x||x — а| < R}

Приведем свойства модуля действительного числа, которые вытекают из определения модуля и свойств арифметических операций.

1) ∣x∣ ≥ 0,2) ∣x∙y∣ = ∣x∣∙∣y∣,3) = 4) ∣x∣ = ∣x∣ если ∃x,5) |x| = |- x|,6) |x| ≤ a ⇔ -a ≤ x ≤ а для ∀a > 0,7) ∣x + y∣ ≤ |x| + |y|,8) ∣x — y∣ ≤ |x| — |y|.

Заметим, что из свойств модуля и того факта, что арифметический корень квадратный неотрицателен, следует, что корень квадратный из полного квадрата некоторого выражения а равен модулю этого выражения: (2.3) √a² = |a|.

Так, например, √5² =5; √(-3)² = 3(а не — 3); √(x + 5)² =| x + 5|.

Аналогичное замечание справедливо при любом сокращении и показателя корня и степени подкоренного выражения на четное число:(2.4) ∀k, n ∈ N

История

Прилагательное Ca Ртезианец относится к французскому математику и философу Рене Декарту, опубликовавшему эту идею в 1637 году. Она была независимо открыта Пьером де Ферма, который также работал в трех измерениях, хотя Ферма не опубликовал открытие. Французский священнослужитель использовал конструкции, подобные декартовым координатам, задолго до времен Декарта и Ферма.

И Декарт, и Ферма использовали одну ось в своих трактах и ​​имеют переменную длину, измеряемую в ссылку на эту ось. Концепция использования пары осей была введена позже, после того, как La Géométrie Декарта была переведена на латынь в 1649 году Франсом ван Скутеном и его учениками. Эти комментаторы представили несколько концепций, пытаясь прояснить идеи, пытаясь в работе Декарта.

Развитие декартовой системы координат сыграло бы фундаментальную роль в развитии исчисления по Исаак Ньютон и Готфрид Вильгельм Лейбниц. Двухкоординатное описание плоскости было обобщено до концепции векторных пространств.

Многие другие системы координат были разработаны со времен Декарта, такие как полярные координаты для плоскости, и сферические и цилиндрические координаты для трехмерного пространства.

Ориентация и рука

В двух измеренийх

правой руки

Фиксация или выбор оси x определяет ось y до направления. А именно, ось y обязательно представляет собой , перпендикуляр оси x через точку, отмеченную 0 на оси x. Но есть выбор, какую из двух половинных линий на перпендикуляре обозначить как положительную, а какую как отрицательную. Каждый из этих двух вариантов определяет различную ориентацию (также называемую хиральностью) декартовой плоскости.

Обычный способ ориентирования плоскости с положительной осью X, направленной вправо, и положительной осью Y, направленной вверх (причем ось X является «первой», а ось Y — «второй» ось) признанной положительной или стандартной ориентацией, также называемой правой ориентацией.

Обычно используемый мнемоник для определения положительной ориентации — это правило правой руки. Поместите несколько сжатую правую руку на плоскость с большим пальцем вверх, указав от оси x к оси y в положительно ориентированной системе координат.

Другой способ ориентировать — это следовать правилам левой руки, положив левую руку на плоскость большим пальцем вверх.

Когда большой палец направлен от начала оси вдоль оси в положительную сторону, кривизна пальцев указывает на положительное вращение вдоль оси.

Независимо от правил, используемой для ориентации плоскости, вращение системы координат сохранит ориентацию. Переключение любых осей изменит ориентацию на обратную, но переключение оставит ориентацию сохранить.

В трех измеренийх

После задания осей x и y они определяют линию , вдоль которой должна лежать ось z, но есть две возможные ориентации для этой линии. Возникающие в результате двух возможных систем координат называются «правая» и «левая». Стандартная ориентация, при которой плоскость xy горизонтальна, а ось z направлена ​​вверх (а ось x и y образуют положительно ориентированную двумерную систему координат в плоскости xy, если смотреть сверху на плоскость xy) называется правосторонней или положительной .

. Название происходит от правой руки. Если указательный палец правой руки направлен вперед, средний палец согнут под прямым углом к ​​нему, а большой палец расположен под прямым углом для обоих пальца указывает относительную ориентацию осей x, y и z в правой системе. Большой палец указывает ось x, указательный палец — ось y, средний палец — ось z. И, если то же самое проделать левой рукой, получится наоборот левосторонняя система.

На рисунке 7 изображены левая и правая системы координат. Отображение трехмерного объекта на двухмерном изображении показано на рисунке. Ось, направленная вниз (и вправо), также есть для направления на наблюдателя, тогда как «средняя» ось для направления в сторону от наблюдателя. Красный круг параллелен горизонтальной плоскости xy и указывает вращение от оси x к оси y (в обоих случаях). Следовательно, красная стрелка проходит перед осью z.

Рисунок 8 — еще одна попытка изобразить правую систему координат. Опять же, возникает неоднозначность, вызванная проецированием трехмерной системы координат на плоскость. Многие наблюдатели видят рисунок 8 как «переворот» между выпуклым кубом и вогнутым «углом». Это соответствует двум возможным ориентациям пространства. Если смотреть на фигуру как выпуклую, это дает левую систему координат. Таким образом увидеть «правильный» способ просмотра рисунка 8 — представить ось x как указывающую в сторону наблюдателя и, таким образом, в изогнутом углу.

Презентация на тему: » Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское.» — Транскрипт:

2

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское

3

Прямоугольной системой координат на плоскости называется… две взаимно перпендикулярные прямые с выбранным на них началом отсчета, единичным отрезком и положительным направлением по каждой оси. x y Как называется горизонтальная ось? Ось абсцисс Ось ординат Как называется точка пересечения координатных прямых? Начало координат Как называется вертикальная ось?

4

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское y x Чем определяется положение точки на координатной плоскости? Как записывают координаты точки? М(х;у) Как называется первая координата? Как называется вторая координата? ордината абсцисса

5

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское y x (-1;-7)(4;8)(-3;-2) (6;0)(-5;4) (-8;0) (0;-7)(0;8) (0;4)(0;4) (0;-2) (0;-5) Ветер по морю гуляет И кораблик подгоняет; Он бежит себе в волнах На раздутых парусах… Но что это на линии горизонта? Поднять команду на борт

6

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское (-3;-3) y x (-1;-2) 2 -2 (2;-2) 4 (4;-2) -4 3 (3;-4) (0;-4) 0 -6 (-6;0) -2 1 (-2;1) (-5;-3) -4 (-4;-1) (-4;4) (3;0) 2 (2;1) -4 3 (0;3) -5 2 (-5;2) 3 3 (3;4) 5 (5;3) (-1;4) 4 -3

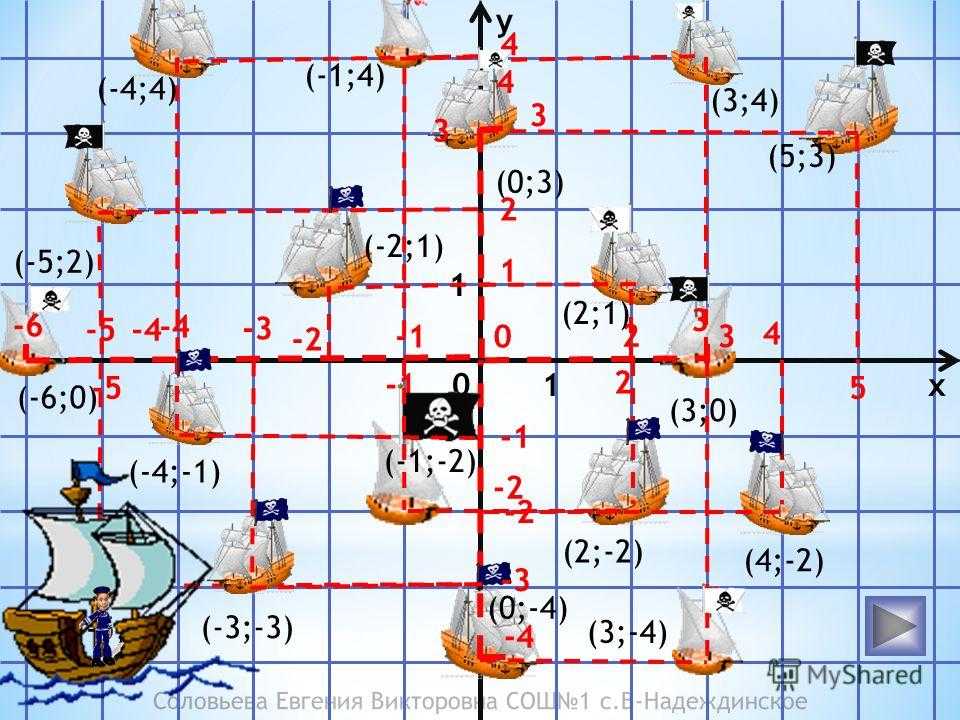
7

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское y x 0 1 1

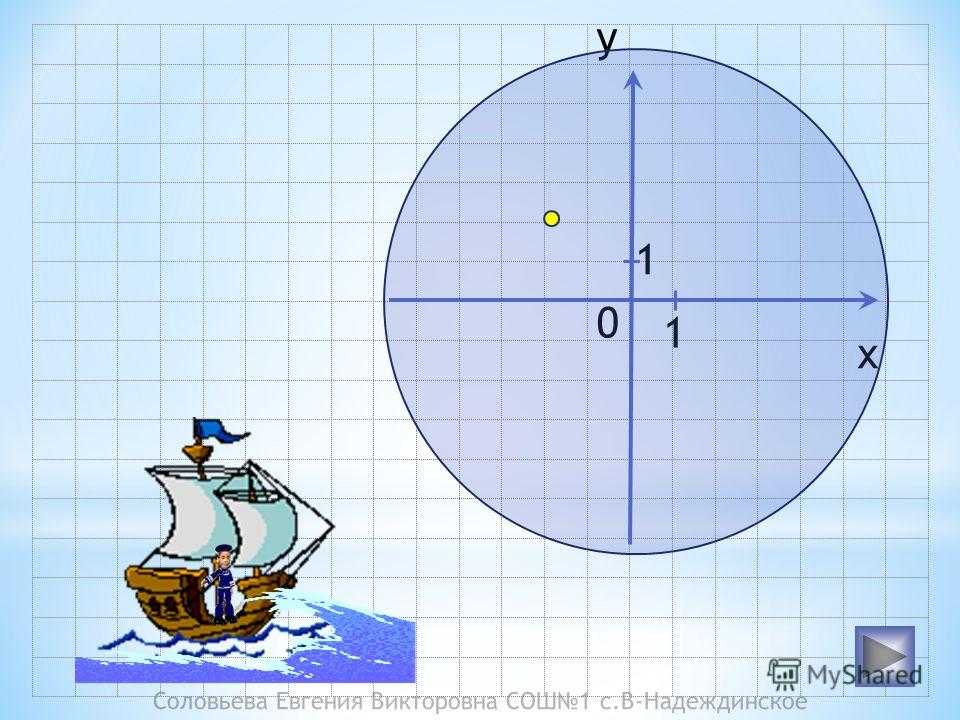
8

y x A(-17;0)Z(-14;-1)Y(-11;-1)X(-12;-2)W(-8;-2)V(-7;-3)T(-4;-4)S(-6;-2)O(6;-3)R(5;-1)P(8;-4)U(7;-2)Q(7;0) N(12;6)M(10;5) L(7;3) K(5;1) H(-3;3)G(-1;7)F(0;8) E(-2;7) D(-6;3) C(-8;3) B(-13;2) A(-17;0) A B C D E F G H K L M N Q U P O R S T V W X Y Z Ребята, чтобы мы вас пропустили, вы должны накормить нас рыбой, но не простой, а той которая плавает в III координатной четверти.

9

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское y x (-6;-9) (-4;-2) (7;-3) (9;5) (-16;-1) (-5;-5) (-11;5)

10

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское Ребята, мы отдадим вам карту сокровищ, если пройдете тест. Говорят, вы знатоки координатной плоскости. Давайте проверим.

11

На сколько частей прямоугольная система координат делит плоскость? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! 5 частей 2 части 4 части

12

Как называются эти части? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! Координатные четверти Координатные плоскости Четвертинки

13

Где на координатной плоскости лежат точки, ординаты которых равны нулю? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! На оси абсцисс В IV координатной четверти На оси ординат

14

В какой координатной четверти лежит точка К(4;-7)? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! В I координатной четверти В IV координатной четверти В III координатной четверти

15

В какой координатной четверти лежит точка М(-5;8)? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! В I координатной четверти В IV координатной четверти Во II координатной четверти

16

Где на координатной плоскости лежат точки, абсциссы которых равны нулю? ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! На оси абсцисс На оси ординат В III координатной четверти

17

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское Вы хорошо потрудились и заслужили карту сокровищ, но расшифровать вам её придется самим. Отметьте на координатной плоскости точки А(-7;5),В(5;7),С(9;-1), D(-4;-4). В точке пересечения отрезков AC и BD зарыт клад. Найдите координаты клада.

18

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское (1;2) y x A(-7;5) B(5;7) C(9;-1) D(-4;-4)

19

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское

20

Если вы читаете эту записку, значит вы дошли до конца и с помощью ЗНАНИЙ победили пиратов, избежали нападения акул, обхитрили дракона. Надеюсь, вы поняли, что главное это не драгоценные камни и золото, а ЗНАНИЯ, которые вы пронесете через всю жизнь. Желаю удачи! Капитан Флинт.

21

Соловьева Евгения Викторовна СОШ1 с.В-Надеждинское Интернет-ресурсы: — Савченко Е.М. (шаблон теста) — анимационные картинки

Координатная ось — «фотография» чисел в виде точек на прямой ##

пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.

Чтобы из любой прямой получить координатную ось ,необходимо выбрать на ней нулевую точку$0$- это будет началом отсчета ;отметитьточку$1$ — определить единичный отрезок(т.е. выбрать масштаб)инарисовать стрелочку в положительном направлении отсчёта .На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу$3$на координатной прямойсопоставляется единственная точка$A$, точке$B$-единственное число$-2$, такое число назвали координатой.

Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.

пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.

Координаты точек на прямой.

пробa Точка$O$разбиваетпрямую$AB$на два луча$OA$и$OB$ . Если примем точку$O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось .Рассмотрим на ней произвольную точку .Как определить ее положение?Для ответа на этот вопрос придумали понятие — координата . Положение любой точки на координатной осизадается её координатой.Чтобы отличить друг от друга координаты , перед числами на левом луче$OA$условились ставить знак «минус », а перед числами на правом луче$OB$-знак«плюс».

Координатысо знаком»$-$»называются отрицательными.Координатысо знаком «+» называютсяположительными .

Точка$O$- начало отсчета илиначало координат , изображает ноль.Само число$0$не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .

Координата точки — это число , показывающее положение точки на прямой.

Записывают координаты точек$B$,$C$,$D$следующим образом:$B(-4,2)$,$C\left(-\frac{1}{2}\right)$,$D(3,9)$.

Изображение чисел точками на координатной оси.

Числа на координатной прямой выглядят точками. Для тогочтобыпостроитьточку, соответствующую некоторому числу$a$ , нужно:определить знак этого числа ;от начала координат отложить отрезок , равный$\left|a\right|$вправо , если знак»+»ивлево , еслизнак»-» .

Число$a$в таком случае называют координатой построенной точки .

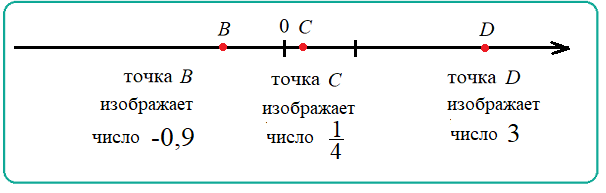
На рисунке числа $3$, $\frac{1}{4}$,$-0,9$изображены соответсвенно точками$B$,$C$,$D$. Числа- это«адреса»точек на координатной прямой.Точки-это»фотографии» чисел.

Введение оси координат:
1) Выбрать на прямой начало координат;
2) Выбрать положительное направление;
3) Выбрать единичный отрезок.

Координаты точки:
Каждой точке можно присвоить свою координату-это расстояние от точки до начала координат с учетом знака: слева от $0$знак $-$ , справа$+$.

Изображение числа : пробa
По любой координате можно восстановить точку.

1.2.1. Декартова система координат window.top.document.title = «1.2.1. Декартова система координат»;

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

График 1.2.1.1.Декартова система координат

В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат; координаты обычно обозначаются латинскими буквами x, y, z и называются, соответственно, абсциссой, ординатой и аппликатой. Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.

График 1.2.1.2.Координаты точки в декартовой системе координат

Важно отметить, что порядок записи координат существенен; так, например, точки A (–3; 2) и B (2; –3) – это две совершенно различные точки. Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям

Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) или B (x; y). В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6)

Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям. Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) или B (x; y). В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6).

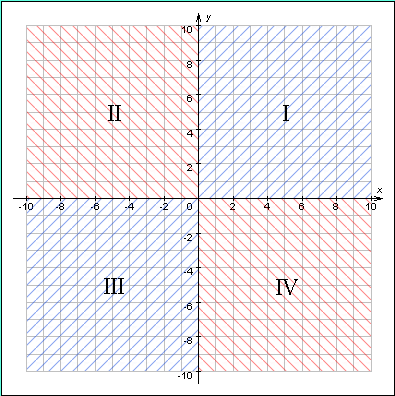Рисунок 1.2.1.1.Координатные оси делят координатную плоскость на четыре квадранта (четверти). Точки, лежащие на осях координат, не принадлежат ни одному квадранту

В двухмерной системе координат все точки, лежащие над (под) осью OX, образуют верхнюю (нижнюю) координатную полуплоскость. Все точки, лежащие правее (левее) оси OY образуют правую (левую) координатную полуплоскость.

Модель 1.5. Расстояние между городами

В конце этого параграфа приведем некоторые очевидные формулы.

• Расстояние от точки A (x; y) до оси OX равно |y|.
• Расстояние от точки A (x; y) до оси OY равно |x|.

• Расстояние от точки

  до начала координат равно

• Расстояние |AB| между точками A (x₁; y₁) и B (x₂; y₂) равно

• Точка M, которая является серединой отрезка AB, где A (x₁; y₁) и B (x₂; y₂), имеет координаты

График 1.2.1.3.Координаты середины отрезка

На случай трехмерного пространства эти формулы обобщаются следующим образом:

• Расстояние от точки A (x; y; z) до плоскости OYZ равно |x|.

• Расстояние от точки A (x; y; z) до начала координат равно

• Расстояние |AB| между точками A (x₁; y₁; z₁) и B (x₂; y₂; z₂) равно

• Координаты точки M, которая является серединой отрезка AB, где A (x₁; y₁; z₁) и B (x₂; y₂; z₂) равны

Продолжаем решать задачи вместе

Пример 6. В декартовой системе координат на плоскости даны точки

Пример 7. В декартовой системе координат на плоскости даны точки

Найти координаты точек, симметричных этим точкам относительно начала координат.

Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:

Пример 8. В декартовой системе координат в пространстве даны точки

Найти координаты проекций этих точек:

1) на плоскость Oxy ;

2) на плоскость Oxz ;

3) на плоскость Oyz ;

1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :

2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :

3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :

Пример 9. В декартовой системе координат в пространстве даны точки

Найти координаты точек, симметричных этим точкам относительно:

7) начала координат.

По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.

4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:

5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:

6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:

7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:

2.3 Геодезическая система координат

С геодезической системой координат связывают понятия геодезической
широты, долготы и высоты. Геодезическая широта В есть угол, под которым
пересекается нормаль к поверхности эллипсоида с плоскостью экватора. Долгота
— двугранный угол между плоскостью нулевого меридиана и плоскостью
меридиана, проходящего через заданную точку.

Геодезические широта и долгота отличаются от соответствующих астрономических
координат, связанных с отвесной линией, так как отвесная линия не совпадает
с нормалью к эллипсоиду. Отклонение отвесной линии можно спроецировать на
две плоскости: плоскость меридиана и плоскость первого вертикала. Нетрудно
понять, что обе эти составляющие можно определить через разности между
астрономическими и геодезическими координатами

(2.2)

Отклонения отвесной линии составляют, как правило, первые несколько секунд
дуги.

Заметим, что геодезическая и геоцентрическая долготы совпадают. Обе они
определены как двугранный угол между плоскостью нулевого меридиана и
плоскостью, содержащей ось вращения и заданную точку. Геоцентрическая же
широта отличается от геодезической.

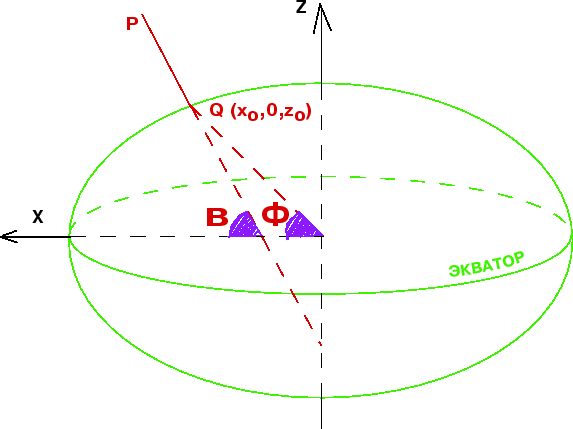
Рассмотрим точку , лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на
поверхность эллипсоида и продолжим его до пересечения с экваториальной
плоскостью ().
Проекцию точки на поверхность эллипсоида обозначим через
Тогда отрезок PQ есть геодезическая высота точки .
Угол, под которым упомянутый
перпендикуляр пересекает плоскость экватора, есть геодезическая широта . Она
относится как к точке , так и к точке . Геоцентрические широты этих двух
точек, как видно из рисунка, различаются. Геоцентрическая широта точки угол
между радиус-вектором этой точки и плоскостью экватора.

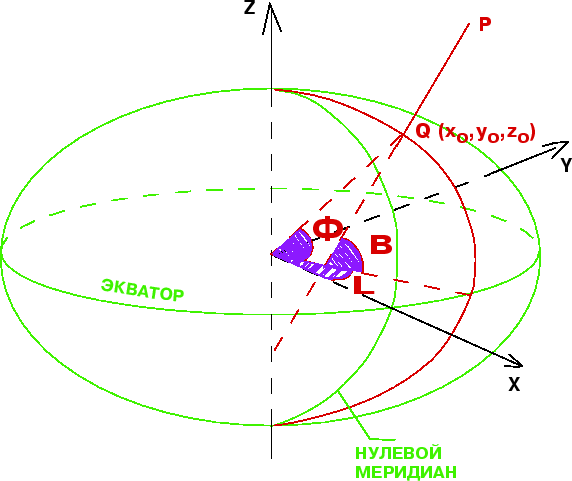Рис. 2.

Установим связь между координатами точки , сжатием эллипсоида и
широтами и . Поскольку точка лежит на поверхности эллипсоида, то ее
прямоугольные координаты
подчиняются уравнению
эллипсоида вращения:
. Рассмотрим сечение .
Тогда, как легко
видеть,
. Чтобы
определить , нужно найти угловой коэффициент нормали в точке .
Уравнение
нормали к кривой в точке
имеет вид

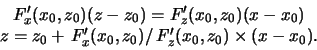(2.3)

У нас
,
поэтому
,

,

Следовательно,

Определим отличие геоцентрической широты от геодезической .
Имеем очевидные равенства

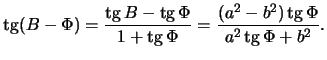(2.4)

Второй эксцентриситет эллипса, как мы знаем, определяется следующим образом

, поэтому

Для Земли второй эксцентриситет мал, поэтому, пренебрегая малыми второго
порядка относительно сжатия, получим
. Можно
также считать, что

Учитывая сказанное, получим

Наибольшее отличие геодезической широты от геоцентрической достигается на
широте 45° и составляет
.

Связь глобальных декартовых координат с геоцентрическими определяется
формулами (). Определим теперь формулы, связывающие декартовы
координаты с
геодезическими. Это означает, что бы должны определить координаты точки
через параметры эллипсоида и геодезические широту и долготу.

Поскольку
, для определения координат , , точки
достаточно, для начала,
определить только координаты и ,
то есть все рассуждения проводить только
для сечения . Обратимся к .

Рис. 3.

Определим прямоугольные координаты точки , расположенной на высоте Н над
поверхностью эллипсоида. Сначала определим координаты проекции точки на
поверхность эллипсоида (точка ). Ее координаты в сечении Охz равны

Индексом «0» мы отметили принадлежность координат к точке, лежащей на
поверхности эллипсоида. Как мы видели

поэтому

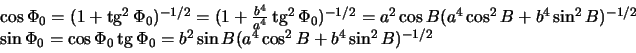
Остается определить радиус-вектор точки .
Воспользуемся уравнением эллипса
и выполним необходимые преобразования.

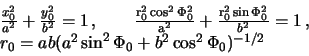(2.5)

Выразим
и
через и
, для чего
воспользуемся приведенными выше формулами. Определим радиус-вектор точки

следовательно,

(2.6)

Обозначим

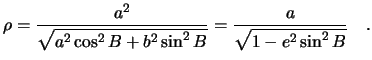(2.7)

Теперь

(2.8)

Для произвольного сечения, проходящего через ось вращения ,
будем иметь

(2.9)

Теперь поднимем точку на высоту Н и совместим ее с точкой .
Прямоугольные координаты изменятся на

(2.10)

Окончательно, теперь формулы для пересчета геодезических координат и Н в
прямоугольные примут вид

(2.11)

Здесь , определенный формулой () имеет простой геометрический смысл:
он равен отрезку нормали, проходящей через точку , от этой точки до точки
пересечения ее с осью вращения эллипсоида. Справедливость этого утверждения
предлагается доказать самостоятельно.