Вычисление радиуса окружности, описанной около треугольника

Формулы площади квадрата

Альберт Эйнштейн и формула площади квадрата

Однажды, в одном городе, жил-был ученый по имени Альберт Эйнштейн. Он был известен своими открытиями в области физики и математики, но однажды он столкнулся с проблемой, которая казалась ему неразрешимой.

Однажды Альберт решил провести эксперимент, чтобы доказать свою теорию о том, что площадь квадрата равна квадрату его длины. Но как он ни старался, он не мог найти способ, как это сделать.

Он провел множество экспериментов, использовал различные методы и инструменты, но все было напрасно.

В конце концов, он решил обратиться за помощью к своим коллегам-ученым.

Когда он пришел к ним, они были удивлены его просьбой. Они сказали ему, что это невозможно, потому что площадь квадрата не может быть выражена в виде формулы.

Но Альберт не сдавался. Он продолжал искать решение этой проблемы.

И однажды, когда он сидел в своем кабинете, его осенило. Он понял, что площадь квадрата можно выразить в виде формулы, если использовать не длину стороны квадрата, а его диагональ.

И вот, наконец, Альберт нашел решение своей проблемы. Он создал формулу, которая позволяла вычислить площадь квадрата по его диагонали. Это было настоящим прорывом в науке!

С тех пор Альберт стал известен как создатель формулы площади квадрата. Его открытие стало одним из самых важных в истории математики и физики.

Касательная, хорда, секущая к окружности

Касательная

Касательная имеет с окружностью только одну общую точку. Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.а — касательная,А — точка касания,ОА — радиус окружности,a┴OA

Отрезки касательных

Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
а, b  — касательные,

ВС=СА,

∠ВСО=∠ОСА

Угол между касательной и хордой

Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.
а — касательная,А — точка касания,ВА — хорда,∠ВАС= половине градусной меры дуги АВ.

Свойство касательной и секущей

Если через точку, лежащую вне круга провести касательную и секущую, то квадрат длины отрезка касательной равен произведению длин отрезков секущей и ее внешней части.
а — касательная,А — точка касания,CD — секущая,
СА2=СВ*СD.

Свойство хорд

Если хорды пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.
CF, AB — хорды,

CK*KF=AK*KB

Свойство секущих

Если через точку, лежащую вне круга провести две секущие, то произведение длин секущей и ее внешней части одной секущей равно произведению длин секущей и ее внешней части другой секущей.CD, CF — секущие,CD*CB=CF*CA.

Длина окружности. Длина дуги

Длина вычисляется по формуле: С=2πR.
Длина дуги вычисляется по формуле: l=C*α:360 или l=πRα:180. α — градусная мера дуги.

Площадь круга. Площадь сектора. Площадь сегмента

OFB — секторKCA — сегментПлощадь круга вычисляется по формуле: S=πR2.
Площадь сектора вычисляется по формуле: S=πR2 *α : 360.

Площадь сегмента находят как разность площадей сектора и треугольника: S=S сектора КОС — S треугольника КОС.

Описанные многоугольники

В любой треугольник можно вписать единственную окружность. Центр окружности — точка пересечения биссектрис треугольника.

Если в прямоугольный треугольник вписать окружность, то радиус можно найти по формуле: r=(a+b-c):2, где a,b — катеты, с- гипотенуза треугольника.

Если в четырехугольник можно вписать окружность, то суммы длин его противолежащих сторон равны.

a+b=c+d
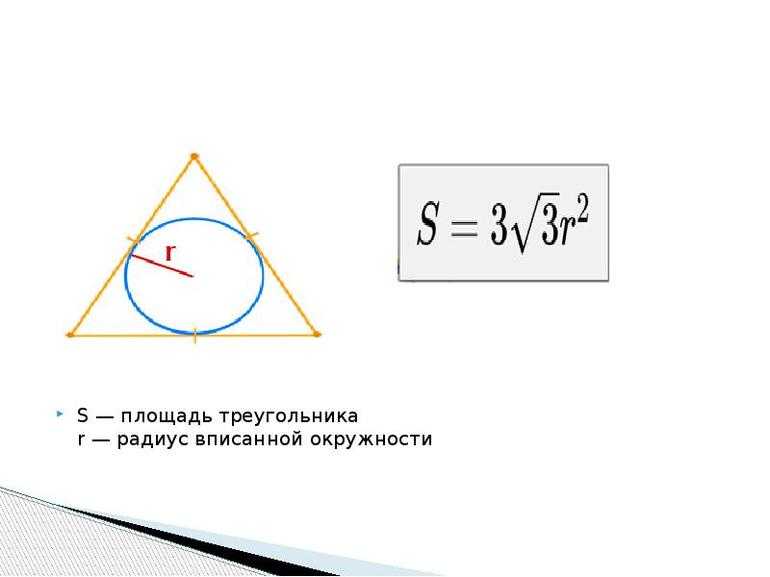
Площадь описанного многоугольника: S=p*r, где р — полупериметр многоугольника, r — радиус окружности.

Вписанные многоугольники

Около любого треугольника можно описать единственную окружность. Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Радиус описанной окружности можно найти по формуле: 2R=a: sin α, где а — сторона треугольника и α — противолежащий ей угол. В прямоугольном треугольнике R=c:2, где с — гипотенуза.

Если около четырехугольника описана окружность, то суммы градусных мер противолежащих углов  равны 180°.∠А+∠С=∠В+∠D=180°

Вписанный в окружность треугольник

Чтобы уметь вычислять площадь описанного треугольника, следует понимать, о каком взаимном расположении многоугольника и окружности идет речь. Согласно определению, если через все вершины полигона проходит окружность, значит, он считается вписанным в нее. Это простое определение не всегда выполняется для произвольного многоугольника, однако, для любой правильной фигуры оно будет справедливым, например, для квадрата или прямоугольника.

Касательно треугольника следует отметить, что он является единственным многоугольником, для которого всегда можно найти центр и радиус описывающей его окружности. Причем независимо от того, какой тип фигуры рассматривается.

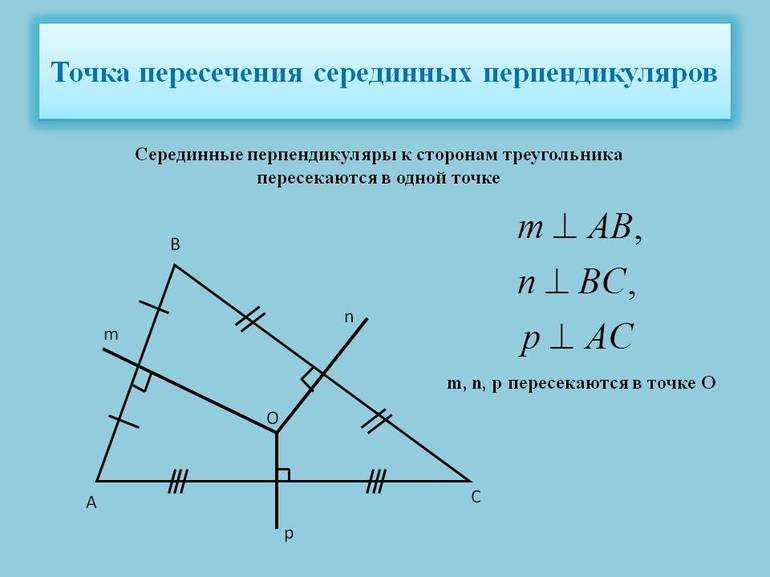
Пересечение медиатрис

В рассматриваемой фигуре имеется три разных медиатрисы. Каждую из них построить несложно для любой из сторон. Для построения следует выполнить последовательность действий:

1. Выбрать сторону.
2. Установить циркуль в один из концов стороны и провести дугу окружности, которая будет пересекать сторону дальше, чем посередине.
3. Пункт 2 выполнить, установив циркуль во второй конец стороны.
4. Соединить точки пересечения дуг в одну линию. Она является медиатрисой.

Из проделанных построений следует один важный факт для всех треугольников: точка пересечения их медиатрис является центром описывающей фигуру окружности. Доказать это утверждение легко. Например, имеется треугольник ABC. Пусть проведена медиатриса m к стороне AB. Любая из точек, принадлежащих прямой m, находится на одинаковом расстоянии от вершин A и B.

Пусть проведена еще одна медиатриса n к стороне BC. Прямые m и n пересекаются в точке O. Поскольку O принадлежит обеим медиатрисам, то она, с одной стороны, находится на одном расстоянии от A и B, с другой стороны, она находится на одинаковой дистанции от вершин B и C. Этот факт дает право сделать вывод о том, что расстояния OA, OB и OC равны. Если их обозначить буквой R, то можно говорить, что R — радиус окружности с центром в точке O, которая проходит через три вершины треугольника, то есть описывается его.

Типы фигур и точка O

Поскольку для треугольника любого типа можно провести описывающую его окружность, то представляет интерес рассмотреть вопрос положения ее центра O. В общем случае существуют три типа рассматриваемого многоугольника:

1. С острыми углами, то есть все они менее 90 °. К этим треугольникам относятся равносторонние. Для них центр описанной окружности всегда расположен внутри фигуры.
2. С одним тупым углом и двумя острыми. Это может быть либо равнобедренный треугольник, либо фигура общего типа. Для нее точка O всегда расположена вне области, ограниченной сторонами многоугольника, то есть за его пределами.
3. Прямоугольный. Для такого типа треугольников центр описанной окружности расположен точно посередине гипотенузы. Это свойство треугольника, которое доказывается просто, если рассмотреть точку пересечения двух средних линий, проведенных относительно катетов. Поскольку O лежит посередине гипотенузы, то последняя является диаметром описанной окружности. Любой треугольник, который опирается на диаметр одной из своих сторон, и третья вершина которого лежит на окружности, является прямоугольным.

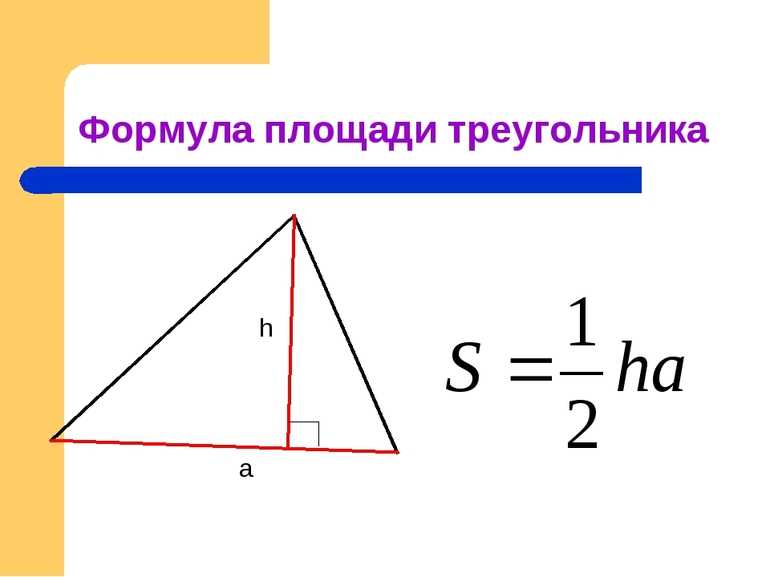
Формулы для определения площади

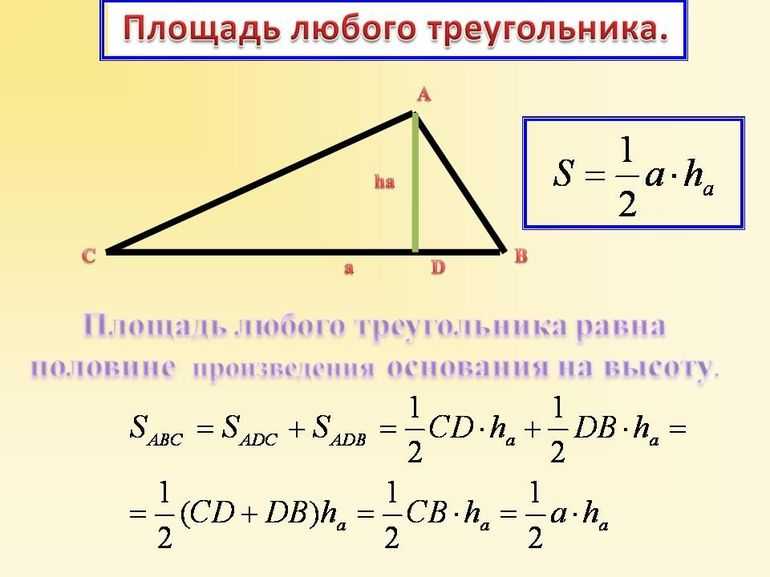
Как известно, площадь треугольника произвольного типа может быть рассчитана, как половина произведения высоты h на длину основания a: S = ½*h*a. Существует также еще одно универсальное выражение для определения S — это половина модуля векторного произведения направляющих отрезков, образующих любые две стороны.

Что касается формул площади треугольника, описанного около окружности, то нужно отметить, что известны несколько из них. Соответствующие равенства имеют следующий вид:

• S = a*b*c/(4*R);
• S = (½*R*ha*hb*hc)^0,5;
• S = 2*R 2 *ha*hb*hc/(a*b*c).

Где a, b, c — длины соответствующих сторон треугольника, ha, hb, hc — высоты, проведенные к a, b и c, соответственно. Видно, что все три формулы требуют знание минимум 4 параметров для рассматриваемой фигуры (радиус и три высоты или три длины сторон).

Полезно также привести формулу для расчета радиуса R:

R = ¼*a*b*c/(p*(p-a)*(p-b)*(p-c))^0,5.

Нужен ли решебник третьеклассникам?

Многим взрослым кажется, что программа этого года не такая уж и сложная, чтобы детям могла понадобиться хоть сколь-нибудь серьезная помощь. Однако при этом они совсем не учитывают, что учителям не хватает времени, чтобы подробно объяснить все нюансы материала, поэтому ребята часто недопонимают, как подступиться к решению заданий. Применяя сборник ответов «Математика 3 класс Учебник Моро М. И. (Просвещение)», ребята получат шанс самостоятельно разобраться в предмете.

Сведениям из пособия вполне можно доверять, так как оно:

• составлено опытными методистами-предметниками;
• соответствует учебной программе;
• отвечает требованиям ФГОС;
• прошел многочисленные проверки на достоверность.

Школьникам часто не хватает усидчивости, чтобы штудировать достаточно объемные параграфы. Кроме того, они иногда не понимают, какая информация важна, а что можно пропустить. Из-за этого их знания носят сумбурный и разрозненный характер. Когда приходит время писать очередной тест или контрольную, ученики не могут собраться с мыслями и допускают одну ошибку за другой. Занятия с решебником помогут учащимся систематизировать свои навыки и успешно справиться с учебной программой этого года.

Теорема об ортоцентрической системе точек

Если в четвёрке точек $A, B, C, H$ точка $H$ является точкой
пересечения высот треугольника $ABC$, то и любая из четырёх точек
является ортоцентром треугольника, образованного тремя остальными
точками.

Доказательство

Рассмотрим треугольник $ABC$, в котором $AA_1, BB_1, CC_1$ – это
высоты, точка $H$ – это ортоцентр.

Докажем, что точка $A$ – это ортоцентр треугольника $BCH$.

Действительно, для треугольника $BCH$ высотами являются $BC_1, HA_1$
и $B_1C$.

А прямые, содержащие эти отрезки, пересекаются в точке $A$.

Аналогично точки $B$ и $C$ являются ортоцентрами для треугольников $ACH$ и $ABH$ соответственно.

Зачем нужно знать формулу площади треугольника?

Формула для расчета площади треугольника может показаться не очень полезной знанием для ребенка, но на самом деле она имеет множество практических применений.

Во-первых, знание формулы площади треугольника поможет детям лучше понять геометрические принципы. Расчет площади является одним из основных понятий геометрии, и строится на основе различных пропорций и связей между сторонами и углами треугольника. Это поможет развить логическое мышление и абстрактное мышление у ребенка, а также повысит их понимание пространственных отношений.

Во-вторых, площадь треугольника может быть использована в реальной жизни для решения разнообразных задач и задачек. Например, зная формулу площади треугольника, ребенок сможет рассчитать площадь участка земли или огорода, площадь фасада здания или шкафа, площадь картинки или стены для расчета необходимого количества краски и многое другое. Эти навыки могут быть полезными в повседневной жизни, а также в будущем при решении математических задач в школе и университете.

Кроме того, знание формулы площади треугольника является необходимым для изучения более сложных геометрических концепций и формул. Оно является основой для изучения других фигур, таких как квадрат, прямоугольник, параллелограмм и т. д. Поэтому, понимание формулы площади треугольника будет полезным в будущем, при изучении более сложных тем геометрии.

Наконец, знание формулы площади треугольника способствует развитию математических навыков у детей. Решение задач на нахождение площади треугольника требует умения правильно применять формулу, а также умения работать с числами и считать. В ходе решения таких задач дети могут прокачать свои навыки вычислений, отработать логику решения задач, а также улучшить навыки использования математических схем и таблиц.

В целом, знание формулы площади треугольника является полезным навыком для детей. Оно поможет им развить логическое мышление, применить математические навыки на практике и облегчит изучение геометрии в школе и университете. Также оно позволит использовать геометрические принципы и решать реальные задачи в повседневной жизни.

Фигура с тремя сторонами

Чтобы понять, как рассчитывать площадь треугольника, вписанного в окружность, необходимо иметь четкое представление о рассматриваемой фигуре. Каждый школьник знает о геометрическом объекте, который ограничен тремя отрезками. Основными элементами треугольника являются следующие:

1. Стороны, которых у фигуры три. Они могут быть равны по длине или отличаться друг от друга. При этом всегда справедливым остается тот факт, что длина любой стороны меньше суммы длин двух других.
2. Вершины — это три точки, которые образованы на пересечении соответствующих сторон. Каждая из них характеризуется определенным значением угла. Для трех углов треугольника справедливо следующее равенство: ∠A + ∠B + ∠C = 180 °, где латинскими буквами названы соответствующие вершины.

Помимо вершин и сторон, треугольник характеризуется дополнительными отрезками, которые часто используются для доказательства теорем и решения геометрических задач. К имеющим специальное название отрезкам относятся такие:

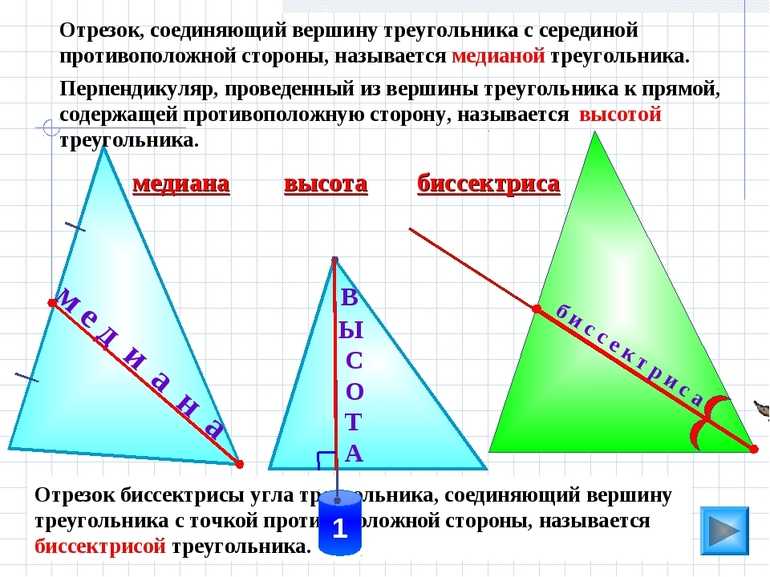
1. Медиана — делящий треугольник на две фигуры с одинаковой площадью отрезок. Он проходит через вершину и середину противоположной стороны. Все три медианы пересекаются в одной точке, которая является массовым центром рассматриваемого геометрического объекта.
2. Биссектриса — отрезок, который делит пополам угол при вершине. Все три биссектрисы, как и медианы, пересекаются в одной точке, которая является центром вписанной в треугольник окружности.
3. Высота — перпендикуляр, который через вершину опускается на противоположную сторону. Высоты часто используются при вычислении площадей.
4. Средняя линия — проходящая через середины двух сторон линия, которая является параллельной третьей. Обе стороны отсекают отрезок, длина которого составляет половину от длины противоположной стороны.
5. Медиатриса или серединный перпендикуляр — это прямая линия, которая пересекает под углом 90 ° сторону треугольника. Важным свойством медиатрис является тот факт, что точка из пересечения — это центр описанной вокруг фигуры окружности.

Влияние ГДЗ на учебный процесс

Третий класс оказывается для ребят намного труднее, чем два предыдущих. В некоторых школах начинается подготовка к ВПР, что увеличивает учебные нагрузки. Помимо этого детям приходится изучать много нового материала, запоминать различные нюансы предметов. Сложнее всего большинству школьников дается математика. Чтобы правильно уяснить все аспекты программы и не наделать при этом много ошибок, стоит воспользоваться «ГДЗ по Математике 3 класс Учебник Моро, Бантова, Бельтюкова (Просвещение)».

Текущие темы весьма трудны, поэтому нужно внимательно подходить к их освоению:

1. Обозначение геометрических фигур буквами.
2. Умножение и деление.
3. Единицы площади.
4. Построение геометрических фигур, симметричных заданным.
5. Приёмы устных вычислений.
6. Виды треугольников, и т.д.

Благодаря работе с пособием ученики получают возможность внимательно проштудировать каждую тему и разобрать все непонятные места из учебника, что позволит им приобрести полноценные навыки. С решебником учащиеся обретут уверенность в своих силах, станут с удовольствием тянуть руку на уроке, чтобы продемонстрировать свои знания.

Практическое применение

Навык расчета периметра и площади треугольников имеет практическое применение в различных сферах жизни. Он часто используется в строительстве, архитектуре, геометрии, судостроении и даже в дизайне.

В строительстве периметр и площадь треугольников используются для расчета длины загородного забора, отделки стен, площади крыши или пола. Зная эти параметры, можно более точно планировать необходимое количество материалов для работ.

В архитектуре и дизайне треугольники широко используются для создания уникальных форм и композиций. Знание периметра и площади помогает архитекторам и дизайнерам рассчитывать размеры и пропорции элементов сооружений и интерьеров.

В геометрии треугольники служат основой для изучения других фигур и их свойств. Расчет периметра и площади треугольников позволяет углубить понимание геометрических принципов и улучшить навыки решения задач.

Использование этих правил поможет учащимся развить логическое мышление, математическую грамотность и применить полученные знания в реальных ситуациях.

Формула площади прямоугольника

Жил-был учёный, который не мог запомнить формулу…

Жил-был один ученый по имени Иван Иванович. Он был очень умный и талантливый, но у него была одна проблема — он не мог запомнить формулы.

Однажды ему нужно было вычислить площадь прямоугольника, и он начал думать: «Площадь прямоугольника равна длине умноженной на ширину». Но как только он начинал писать формулу, его мысли разбегались, и он забывал, что хотел написать.

Тогда Иван Иванович решил пойти к своему другу, который был математическим гением. Он спросил у него, как вычислить площадь прямоугольника. Друг ответил: «Площадь прямоугольника равна удвоенной длине на ширину».
Иван Иванович был очень удивлен, ведь он всегда думал, что площадь равна длине умножить на ширину. Но друг объяснил ему, что если мы удвоим длину, то получим удвоенную площадь, а если удвоим ширину, то получим утроенную площадь.

С тех пор Иван Иванович стал запоминать формулы с помощью картинок. Он рисовал прямоугольник на бумаге, а затем делил его на две части и рисовал еще один прямоугольник внутри первого. Затем он писал формулу площади для каждого прямоугольника и соединял их вместе.
Теперь Иван Иванович мог легко вычислять площадь прямоугольника и не забывать формулы. И он понимал, что это не только помогает ему в учебе, но и делает его более умным и сообразительным.

Теорема (расстояние между ортоцентром и инцентром)

$$HI = \sqrt{4R^2-\dfrac{a^3+b^3+c^3+abc}{2p}}.$$

Доказательство

Чтобы центр масс треугольника попал в инцентр $I$ вершины $A, B, C$ нужно загрузить массами $a, b, c$ соответственно.

Тогда для любой точки $X$ будет верно равенство $$\overrightarrow{XI} = \dfrac{a}{a+b+c}\overrightarrow{XA}+\dfrac{b}{a+b+c}\overrightarrow{XB}+\dfrac{c}{a+b+c}\overrightarrow{XC}.$$

Тогда можно взять вместо точки $X$ ортоцентр $H$:

$$\overrightarrow{HI} = \dfrac{1}{2p}\left(a\cdot \overrightarrow{HA}+b\cdot \overrightarrow{HB}+c\cdot \overrightarrow{HC}\right)$$

Вспомним, что $HA = a\ctg{\alpha}$. Тогда

$HI^2 = \dfrac{1}{4p^2}\left(a\cdot \overrightarrow{HA}+b\cdot \overrightarrow{HB}+c\cdot \overrightarrow{HC}\right)^2 = $

$ = \dfrac{1}{4p^2}\left(a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2+2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC}\right)$

Лемма 0

$$\cos{\alpha}\cos{\beta}\cos{\gamma} = \dfrac{\sin^2{\alpha}+\sin^2{\beta}+\sin^2{\gamma}}{2}-1 = \dfrac{a^2+b^2+c^2}{8R^2}-1$$

Лемма 1

$a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2 = $

$= a^4\ctg^2{\alpha}+b^4\ctg^2{\beta}+c^4\ctg^2{\gamma} = $

$= 16R^4\sin^4{\alpha}\ctg^2{\alpha}+16R^4\sin^4{\beta}\ctg^2{\beta}+16R^4\sin^4{\gamma}\ctg^2{\gamma} = $

$= 16R^4(\sin^2{\alpha}\cos^2{\alpha}+\sin^2{\beta}\cos^2{\beta}+\sin^2{\gamma}\cos^2{\gamma}) = $

$= 16R^4(\sin^2{\alpha}-\sin^4{\alpha}+\sin^2{\beta}-\sin^4{\beta}+\sin^2{\gamma}-\sin^4{\gamma}) = $

$= 16R^4\left(\dfrac{a^2}{4R^2}+\dfrac{b^2}{4R^2}+\dfrac{c^2}{4R^2}-\dfrac{a^4}{16R^4}-\dfrac{b^4}{16R^4}-\dfrac{c^4}{16R^4}\right) = $

$=4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)$

Лемма 2

$2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC} = $

$ = +2a^2b^2\ctg^2{\alpha}\ctg^2{\beta}\cos{(180^\circ-\gamma)} + 2b^2c^2\ctg^2{\beta}\ctg^2{\gamma}\cos{(180^\circ-\alpha)} + 2a^2c^2\ctg^2{\alpha}\ctg^2{\gamma}\cos{(180^\circ-\beta)} = $

$ = -2a^2b^2\ctg^2{\alpha}\ctg^2{\beta}\cos{\gamma} — 2b^2c^2\ctg^2{\beta}\ctg^2{\gamma}\cos{\alpha} — 2a^2c^2\ctg^2{\alpha}\ctg^2{\gamma}\cos{\beta} = $

$ = -2\cos{\alpha}\cos{\beta}\cos{\gamma}\left(\dfrac{a^2b^2}{\sin{\alpha}\sin{\beta}}+\dfrac{b^2c^2}{\sin{\beta}\sin{\gamma}}+\dfrac{a^2c^2}{\sin{\alpha}\sin{\gamma}}\right) = $

$ = -2\cos{\alpha}\cos{\beta}\cos{\gamma}\left(4R^2ab+4R^2bc+4R^2ac\right) = $

$ = -2\left(\dfrac{a^2+b^2+c^2}{8R^2}-1\right)4R^2\left(ab+bc+ac\right) = $

$ = 4R^2\left(2ab+2bc+2ac\right)-(a^2+b^2+c^2)(ab+bc+ac)$

продолжение доказательства

Тогда

$HI^2 = \dfrac{1}{4p^2}\left(a^2 \overrightarrow{HA}^2+b^2 \overrightarrow{HB}^2+c^2 \overrightarrow{HC}^2+2ab\overrightarrow{HA}\cdot\overrightarrow{HB}+2bc\overrightarrow{HB}\cdot\overrightarrow{HC}+2ac\overrightarrow{HA}\cdot\overrightarrow{HC}\right) =$

$= \dfrac{1}{4p^2}\left(4R^2(a^2+b^2+c^2)-(a^4+b^4+c^4)+4R^2\left(2ab+2bc+2ac\right)-(a^2+b^2+c^2)(ab+bc+ac)\right) = $

$= \dfrac{1}{4p^2}\left(4R^2(a^2+b^2+c^2+2ab+2bc+2ac)-(a^4+b^4+c^4+(a^2+b^2+c^2)(ab+bc+ac))\right) = $

$= \dfrac{1}{4p^2}\left(4R^2(a+b+c)^2-(a^4+b^4+c^4+a^3b+a^2bc+a^3c+ab^3+b^3c+b^2ac+abc^2+bc^3+ac^3)\right) = $

$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^4+a^3b+a^3c+ab^3+b^4+cb^3+ac^3+bc^3+c^4+a^2bc+ab^2c+abc^2)\right)=$

$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^3(a+b+c)+b^3(a+b+c)+c^3(a+b+c)+abc(a+b+c))\right) =$

$= \dfrac{1}{4p^2}\left(16R^2p^2-(a^3+b^3+c^3+abc)2p\right) =$

$= 4R^2-\dfrac{a^3+b^3+c^3+abc}{a+b+c}$

Ответ

Проверено экспертом

Центр вписанной окружности в равносторонний треугольник лежит на высоте (биссектрисе и медиане) и делит её в отношении 2/1 считая от вершины. ⇒ высота (7+7*2)=21 ед.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера»

Равносторонний треугольник — треугольник, у которого все стороны равны.

Какие же особенные свойства присущи равностороннему треугольнику?

Равносторонний треугольник. Свойства

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны .

Естественно, не правда ли? Три одинаковых угла, в сумме , значит, каждый по .

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник:

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром! В равностороннем треугольнике оказалось не особенных линий, как во всяком обычном треугольнике, а всего три!

  Посоветуйте интересную книгу форум

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной.

Уже должно быть очевидно, отчего так.

Посмотри на рисунок: точка – центр треугольника. Значит, – радиус описанной окружности (обозначили его ), а – радиус вписанной окружности (обозначим ).

Но ведь точка – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении , считая от вершины.

Поэтому , то есть .

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.

Рассмотрим – он прямоугольный.

Равносторонний треугольник. Радиус описанной окружности

Мы уже выяснили, что точка – не только центр описанной окружности, но и точка пересечения медиан. Значит, .

Величину мы уже находили. Теперь подставляем:

Равносторонний треугольник. Радиус вписанной окружности

Это уже теперь должно быть совсем ясно

Ну вот, все основные сведения обсудили. Конечно, можно задавать сотни вопросов про всякие длины всяких отрезков в равностороннем треугольнике.

Но главное, что следует иметь в виду, решая задачки о равностороннем треугольнике, – это то, что все его углы известны – равны и все высоты являются и биссектрисами, и медианами, и серединными перпендикулярами.

Равносторонний треугольник. краткое изложение и основные формулы

Равносторонний треугольник — треугольник, у которого все стороны равны: .

В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой, которые проведены из той же вершины Точки пересечения высот, биссектрис, медиан и серединных перпендикуляров равностороннего треугольника совпадают.

  С чем можно поесть сгущенку

Центры вписанной и описанной окружностей равностороннего треугольника совпадают: точка . В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной: .

В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны :

Высота=медиане=биссектрисе : Радиус описанной окружности : Радиус вписанной окружности : Площадь : Периметр :

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

• Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
• Площадь треугольника равна произведению ПЕРИМЕТРА на радиус!
• Площадь треугольника равна произведению ПОЛУПЕРИМЕТРА на радиус вписанной окружности

Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

Из формулы , где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности:

Равносторонний треугольник вписан в окружность найти радиус Ссылка на основную публикацию