Как пишется высота в математике

Задачи на показатель преломления

№2.
Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с: v.

Решение.
Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ.
Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3.
Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи.
Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.

Решение.
В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ.
Значение угла преломления — 26º.

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = aba = 6, b = 2S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = abS = 12, a = 6, b = x12 = 6 × xx = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2a = 8S = 82 = 64 см2Ответ: площадь квадрата со стороной 8 см равна 64 см2

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abca = 6, b = 4, c = 3V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abcV = 200, a = 10, b = 5, c = x200 = 10 × 5 × x200 = 50xx = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.

Решение

a — длинаb — ширинаc — высота

a = 42 мb = мc = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525a = 5.8b = 3.5c = x

35,525 = 5,8 × 3,5 × x35,525 = 20,3 × xx = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

1.1.8 Дифференцирование векторов

Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.

Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.

По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:

~u = ~u(t + t) ~u(t):

Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис

1.6
(напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).

~u(t) ~u

Рис. 1.6. Изменение вектора

Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:

При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_
не слишком хорошо смотрится) и ограничиваемся обозначением (1.18
). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.

Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.

Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от

предела в правой части (1.18
) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.

Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.

Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.

1. Постоянный скалярный множитель выносится за знак производной: если c = const, то

d(c~u) = c
d~u:
dt dt

Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона

будет переписан в виде:

2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt
d
(x(t)~c) = x(t)~c:

3. Производная суммы векторов равна сумме их производных:

dt
d
(~u + ~v) =d~u
dt
+d~v
dt
:

Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7
).

Рис. 1.7. Разложение вектора по базису

Как известно, любой вектор ~u единственным образом раскладывается по базису единичных

векторов ~
,~
,~
: i j k

~u = ux
i + uy
j + uz
k:

Здесь ux
, uy
, uz
проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.

Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux
, uy
, uz
являются функциями времени:

~u(t) = ux (t) i	Uy (t) j	Uz (t)k:

Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:

ux (t)~ i +

uy (t)~ j

uz (t)~ k:

Затем выносим постоянные векторы за знак производной:

Ux (t)i + uy (t)j + uz (t)k:

Таким образом, если вектор ~u имеет координаты (ux
; uy
; uz
), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux
; uy
; uz
).

Ввиду особой важности формулы (1.20
) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19
) имеем:. ~u(t + t) = ux
(t + t) i + uy
(t + t) j + uz
(t + t)k:

~u(t + t) = ux
(t + t) i + uy
(t + t) j + uz
(t + t)k:

Напишем изменение вектора ~u:

~u = ~u(t + t) ~u(t) =

Ux
(t + t) i + uy
(t + t) j + uz
(t + t)k ux
(t) i + uy
(t) j + uz
(t)k =

= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k =
Ux i + uy j + uz k:
Делим обе части полученного равенства на t:
				T i +	t j +

В пределе при t ! 0 дроби ux
= t, uy
= t, uz
= t переходят соответственно в производные ux
, uy
, uz
, и мы снова получаем соотношение (1.20
):

Ux
i + uy
j + uz
k.

Коротко о главном

В соответствии с советским ГОСТ 2.321-84, который заменил более старый ГОСТ 3452—59, для обозначения длины используется латинская буква «L», для ширины – «B», а для высоты – применяется литера «Н». Данные символы утверждены в XX века.

При обозначении обычно величины указываются в следующем порядке: длина, ширина и высота. При этом учитывается контекст и наиболее важный параметр, который пишется в начале. Еще принято первым обозначать наибольший размер из всех других величин. Хотя могут устанавливаться индивидуальные стандарты последовательности указания габаритов для конкретных изделий.

Вопрос

Как пишут длина ширина высота?

длину буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А, высоту или глубину – h, ширину – В.

В каком порядке указываются габаритные размеры?

Габаритные размеры изделия длина 1500 мм ширина 1200 мм высота 2500 мм, есть сомнению что может нужно записать 1500×1200×2500, как прописана во многих формулярах изделий, но вот правильности чередования в ГОСТах (длина×ширина×высота или ширина×длина×высота или…)

Что сначала указывается ширина или высота?

Пусть сначала всегда идёт длина, потом ширина и высота. Так покупателю будет проще привыкнуть к формату. Формат «1450×975×455 мм» вполне понятен и без уточнений, ведь рядом есть картинка. Для многих предметов важны не только габаритные размеры.

Как правильно указать размер картины?

Для произведений живописи указываются размеры по подрамнику или по доске (высота, ширина). Для произведений графики указывается двойной размер (высота, ширина) – листа и изображения. это еще в школе учили: оси X и Y. всегда сначала ширина, а потом высота.

Как правильно обозначать размеры?

Как обозначаются размеры длина ширина высота

Длина	L , l
Ширина	B, b
Высота, глубина	H, h
Толщина (листов, стенок, ребер и т.д.)	s
Диаметр	D, d

В каком порядке идут размеры?

Буквенные значения латиницей: русская расшифровка

Буквенное обозначение	Мужские размары	Женские размеры
M	48	44
L	50	46
XL	52	48
XXL	54-56	50-52

Как указываются размеры сумок?

Высота и ширина сумки: высота измеряется от самой верхней точки до нижнего края (без учета ручки), ширина – между двумя крайними точками по горизонтали. Глубина сумки: измеряется сбоку в самом широком месте. Длина ручки: измеряется от одного конца до другого гибкой сантиметровой лентой.

Как определить что у предмета длина А что ширина?

Ширина – это протяженность между двумя точками плоскости, которые лежат, в отличие от длины, на наименьшем расстоянии друг от друга. То есть, длина – это наибольший размер предмета, а ширина – наименьшей. Нужно помнить, что ширина всегда измеряется в поперечном направлении к длине.

Как обозначают длину и ширину?

Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.

Какие есть размеры картин?

Стандартные размеры картин, плакатов и постеров(европейский ряд, см):18х24, 24х30, 30х40, 35х50, 40х50, 50х60, 50х70, 50х100, 60х70, 60х80, 60х90, 90х120. Стандартные форматы картин и фотографий( см):21х29,7 (формат А4), 29,7х42 (формат А3), 32,9х48,3 (А3+), 42х59,4 (формат А2).

Какой буквой обозначают ширину?

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет.

Какой буквой обозначают высоту?

Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.

Как правильно пишутся размеры?

А писать надо сначала длину (по горизонтали Х), потом ширину (по вертикали Y), потом глубину (по оси Z). Ширина Высота Длина (она же Глубина, она же Толщина) — это те же XYZ.

Как определить размеры мебели?

Размеры указываются в миллиметрах (рис. 1): – ширина, глубина, высота – при описании мебели для хранения и мебели для сидения; – ширина, длина, высота – при описании мебели для лежания и от- дельно стоящих столов.

Как пишутся размеры одежды?

Расшифровка обозначений (значки на ярлыках одежды): «XS» (eXtra small – очень маленький), «S» (small — маленький), «M» (medium – средний), «L» (large – большой размер), «XL» (eXtra Large – очень большой), «XXL» (eXtra eXtra Large – супер-большой), «XXXL» и так далее (подробнее – в таблице).

Размеры длина, ширина, высота

Производство асбоцементных профилей организовано в соответствии госстандартами: 3034095 для волновых и 1812495 для плоских.

Волновые АЦЛ

Хотя состав стройматериала одинаковый, по размерам изделия могут разниться. Это также касается толщины изделия. Как правило, она изменяется в промежутке от 5 до 9 мм. Что же касается ширины, то она определяется количеством волн.

Профиль АЦЛ зависит от формы поперечного сечения и расстояния между волнами. Форма поперечного сечения бывает двух типов – 40 на 150 и 54 на 200. Первое число этого показателя (40 или 54) указывает на высоту волны, а второе (150 или 200), соответственно, на ее шаг. Высота шифера есть не что иное, как длина отрезка, связывающее верх волны и низ без учета толщины профиля.

Вариант шифера	Высота	Ширина	Длина	Шаг волны
7-ми волн.	8-ми волн.	6-ти волн.
40/150/1750	40	980	1130		1750	150
54/200/1750	54			1125	1750	200

На заметкуОтечественные производители имеют право на производство нестандартных АЦЛ на основе собственных ТУ.

Листы с различными профилями классифицируют в три группы:

• ВО – обычный профиль;
• УВ – унифицированный;
• ВУ – усиленный.

• для обычных – 1,2 на 0,68 м;
• для унифицированных – 1,75 на 1,125 м;
• для усиленных длина шифера равна 2,80 м.
• волн современных асбоцементных листов – шесть, семь и восемь. К примеру, стандартный шифер 8 ми волнового – 1,75х1,13 м при толщине – 5,2 или 5,8 мм, величина площади – 1,977 кв. м. У 7-ми и 8-ми — одинаковая высота, ширина же отличается, поскольку количество волн не совпадает.

Плоские АЦЛ

Определенные качества плоских и волновых профилей схожи, тем не менее между ними есть определенные различия. К примеру, плоские могут быть непрессованными, а это значит, что они будут отличаться по своим техническим характеристикам. Следует отметить, что плоские АЦЛ более прочные по сравнению с волновыми. К примеру, их прочность на сжатие и изгиб достигает, соответственно, 90-130 и 20-50 Мпа.

Главное достоинство этого материала, скорее всего, в разнообразии его использования. Всего несколько примеров:

•  достаточно малый вес позволяет использовать плоские профили при устройстве перекрытия, причем дополнительные элементы укрепления при этом не используют.
• довольно часто используется в качестве внутренней и внешней отделки зданий;
• с их помощью возводят перегородки различного типа и вертикальные ограждения.

• длина может быть 2,5, 3,0 и 3,5 м;
• ширина – 1,2 и 1,5 м;
• толщина – 0,6, 0,8 и 1,0 см.

На строительном рынке можно встретить также плоские листы промышленного производства меньших габаритов (длина – 0,6 м, ширина – 0,4 м), которые подходят для устройства кровли.

Следует отметить, что производители изготавливают на заказ профили других габаритов и оттенков. Разработанные красители отличаются устойчивостью не только к воздействиям атмосферы, но и к выгоранию.

2019 stylekrov.ru

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n 21 = v 1: v 2 = n 2: n 1 ,

где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.

Основные понятия

Высота – это расстояние от вершины фигуры до её основания. В математике высота может относиться к различным фигурам: к треугольнику, параллелограмму, трапеции, прямоугольнику, кругу и т.д.

Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на основание или на продолжение этой основания. Высота может быть внутренней, тогда она относится к основанию и находится внутри треугольника, или высота может быть внешней, тогда она продолжает основание за пределы треугольника.

Высота параллелограмма – это отрезок, соединяющий две противоположные вершины параллелограмма, перпендикулярный параллельной стороне.

Высота трапеции – это перпендикуляр, опущенный к основанию трапеции из точки пересечения диагоналей. Если трапеция прямоугольная, то высота является одной из её боковых сторон.

Высота прямоугольника – это любая сторона, перпендикулярная другой стороне.

Высота круга (диаметр) – это отрезок, соединяющий две точки на окружности и проходящий через её центр. Часто вместо термина «высота круга» используется термин «диаметр». Это наибольшее возможное расстояние между двумя точками на окружности.

Все эти понятия высоты в математике широко используются при решении задач по геометрии, которые часто встречаются в учебных заведениях.

Как правильно пишутся размеры высота, ширина, длина обозначения латинскими буквами

Решая геометрические задачи, ученики сталкиваются с вопросом: как правильно обозначить те или иные части чертежа? Например, высоту треугольника, ширину прямоугольника, размеры бассейна. Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила.

Как обозначаются различные параметры

В единой системе измерения используется обозначение латинскими буквами:

Как обозначить глубину?

Почему же для высоты и глубины применяется одна и та же буква? Если вы построите чертеж параллелепипеда, то здесь вы отметите высоту фигуры.

А если составить чертеж прямоугольного бассейна того же размера, что и параллелепипед, то обозначается глубина. Таким образом, можно сказать, высота и глубина в этом случае будут одной величиной.

Понятие «глубина» встречается и в географии. На картах она отображается цветом. Если речь идет о водных просторах, то чем темнее синий, цвет, тем больше глубина, а если речь идет о суше, то низменности обозначаются темно-зеленым цветом.

В черчении эта величина обозначается литерой S. Она позволяет создать полное восприятие объекта иногда даже с одним видом.

Что бывает длинным

Что же такое длина и как обозначается этот показатель? Она указывает расстояние от точки до точки, то есть размер отрезка. В геометрических задачах его принято обозначать как А. В стереометрии ее могут обозначать и А, и l (например, в задачах, где встречается прямая, пересекающая плоскость).

В физике же длина маятника, плеча рычага и т.д. в «Дано» обозначается буквой l, так как речь идет об отдельной прямой.

Отличие длины от высоты

А высота – это перпендикуляр, опущенный на противолежащую плоскость.

То есть можно сделать вывод, что длина от высоты отличается тем, что является частью фигуры, совпадая с ее гранью, а высота получается в результате дополнительного построения на чертеже.

Высоту проводят для того, чтобы получить новые данные для решения задач, а также новых фигур в составе исходной.

Вот такой ширины

Ширина предмета необходима для того, чтобы понять форму как двумерного, так и трехмерного объекта. Как правило, она обозначается буквой В.

Измеряется ширина в метрах (по СИ). Но если предмет слишком мал, то для удобства используют более мелкие единицы измерения:

А если предмет слишком крупный, то пишутся такие приставки:

Как называются стороны прямоугольника?

В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.

Это значит, что стороны, образующие углы различны.

Как правило, более длинную сторону прямоугольника называют длиной, а ширина прямоугольника — это его короткая сторона.

В чем измеряются размеры длины, ширины и высоты по СИ

По единой системе измерения длина, высота и ширина измеряются в метрах. Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.

Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать значения приставок.

После подсчетов эти единицы должны быть переведены в метры.

Существуют также внесистемные единицы, но они встречаются очень редко:

При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы

(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).

А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.

Обозначения длины, ширины, высоты в геометрии

Измеряем геометрические параметры

Теперь вы знаете, какой буквой обозначается длина, в чем измеряется ширина прямоугольника, и сможете сами объяснить любому, как обозначаются различные параметры.

Это интересно! Легкие правила округления чисел после запятой

Соотношение с мебелью

Картины в интерьере не являются частью пустого музейного пространства с белыми стенами, а дополняют помещение, уже наполненное разнообразными предметами мебели, с которыми они должны органично взаимодействовать

Развешивая картины, следует обратить внимание на наличие выступов и ниш, уровень верхнего края дверей и окон, положение мебели

Простые рисунки или орнаменты, повторить который под силу почти каждому, могут органично украсить интерьер. Пример симметричной композиции из работ одинакового формата, Pottery Barn

Совет: вешать картины рядом с высокими шкафами не рекомендуется, а вот крупная картина даже над небольшим каминным порталом будет смотреться весьма эффектно.

Классический вариант размещения картин в гостиной — над диваном или другим крупным, но невысоким предметом мебели

Чаще всего картины группируют на одной из стен комнаты, например, над камином, низким комодом или диваном

В этом случае, важно, проведите воображаемую линию от края предмета обстановки, и расположить картина таким образом, чтобы между ними и этой линией оставалось свободное пространство

Таблица единиц измерения «Электричество и магнетизм»

Физическая величина	Символ	Единица измерения физической величины	Ед. изм. физ. вел.	Описание	Примечания
Сила тока	I			Протекающий в единицу времени заряд.
Плотность тока	j	ампер на квадратный метр		Сила электрического тока, протекающего через элемент поверхности единичной площади.	Векторная величина
Электрический заряд	Q , q		Кл = (А·с)	Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.	экстенсивная, сохраняющаяся величина
Электрический дипольный момент	p	кулон-метр		Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
Поляризованность	P	кулон на квадратный метр	Кл/м 2	Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Напряжение	U			Изменение потенциальной энергии, приходящееся на единицу заряда.
Потенциал, ЭДС	φ, σ			Работа сторонних сил (некулоновских) по перемещению заряда.
	E	вольт на метр		Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Электрическая емкость	C			Мера способности проводника накапливать электрический заряд
Электрическое сопротивление	R, r		Ом = (м 2 ·кг/(с 3 ·А 2))	сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление	ρ			Способность материала препятствовать прохождению электрического тока
Электрическая проводимость	G			Способность тела (среды) проводить электрический ток
Магнитная индукция	B			Векторная величина, являющаяся силовой характеристикой магнитного поля	Векторная величина
Магнитный поток	Ф		(кг/(с 2 ·А))	Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля	H	ампер на метр		Разность вектора магнитной индукции B и вектора намагниченности M	Векторная величина
Магнитный момент	p m	ампер-квадратный метр		Величина, характеризующая магнитные свойства вещества
Намагниченность	J	ампер на метр		Величина, характеризующая магнитное состояние макроскопического физического тела.	векторная величина
Индуктивность	L			Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Электромагнитная энергия	N		Дж = (кг·м 2 /с 2)	Энергия, заключенная в электромагнитном поле
Объемная плотность энергии	w	джоуль на кубический метр	Дж/м 3	Энергия электрического поля конденсатора
Активная мощность	P			Мощность в цепи переменного тока
Реактивная мощность	Q			Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Полная мощность	S	ватт-ампер		Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях — мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

постоянная Авогадро;

увеличение оптического прибора;

концентрация вещества;

число Дебая;

полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

показатель преломления, причем он может быть абсолютным или относительным;

нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так — нет информации.

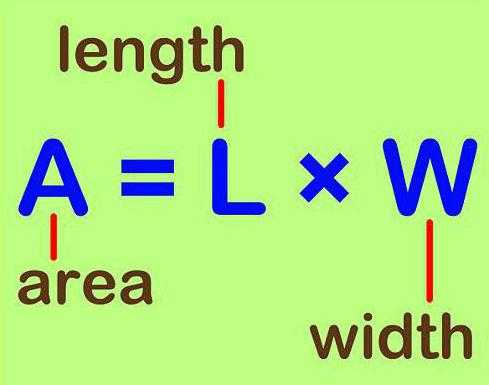
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь — это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).