История возникновения цифр и чисел.
Я узнал что первое доказательство использования древними людьми счета — это волчья кость, на которой 30 тысяч лет назад сделали зарубки.
счет появился более 30 тысяч лет назад

Если уж своих пальцев не хватало, звали приятеля, чтобы уже считать на его руках и ногах. Но такой способ был неудобен.
При ведении хозяйства, при общении с соплеменниками человек использовал пальцы рук, а иногда и ног, чтобы посчитать, например, количество голов скота в стаде, или показать, сколько мужчин пойдет сегодня на охоту.
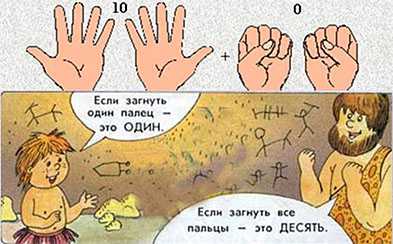
Потом начали применять для счета подручные материалы (камушки, палочки…)
Цифры появились у разных народов в разное время.
индейцы майя

В Древнем Египте около 7 тысяч лет назад использовали такую запись чисел: единица обозначалась палочкой, сотня — пальмовым листом.
А сто тысяч — обозначалось лягушкой (в дельте Нила было очень много лягушек, вот у людей и возникла такая ассоциация: сто тысяч — очень много, как лягушек в Ниле).
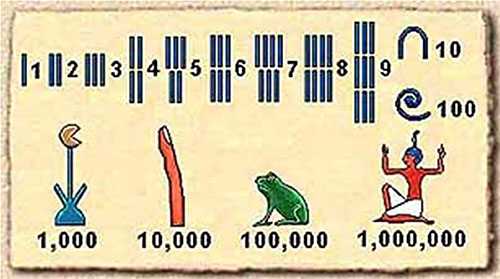
Римские цифры появились 2500 лет назад. С небольшими числами эта форма записи вполне удобна, но для записи больших чисел очень сложна. И с ними неудобно проводить вычисления. Сейчас римские цифры тоже применяют, например, в записи века, порядкового номера монарха и т.п.

Индейцы и народы Древней Азии при счете завязывали узелки на шнурках разной длины и цвета.
счетной книги
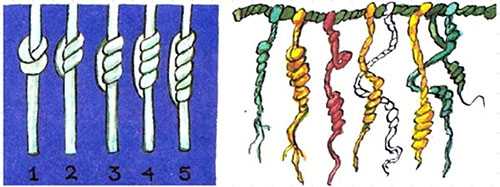
В V веке в Индии появилась система записи чисел, которая является основой для современных цифр. Индия была оторвана от других стран, — на пути лежали тысячи километров расстояния и высокие горы.
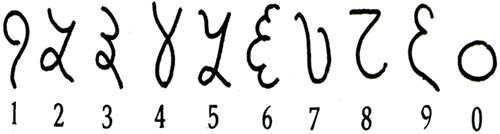
Арабы были первыми «чужими», которые заимствовали цифры у индийцев и привезли их в Европу.
цифры имеют арабское происхождение

Арабы немного видоизменили индийскую систему записи цифр, приспособив к своему письму. Но с течением времени цифры видоизменялись.
Считается, что арабские математики для удобства решили привязать количество углов в записи цифры к его численному значению. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
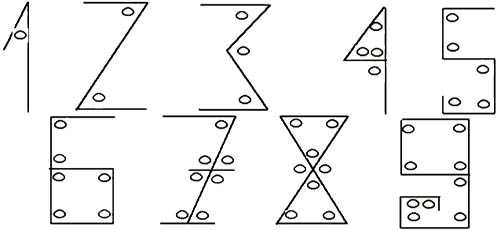
Привычные нам формы цифр, более округлые, потому что угловатые цифры писать долго и не очень удобно.
Но, я заметил, что угловатые цифры все же используются и в нашей жизни при написании индекса на конверте, цифр в электронных часах и калькуляторах.

Хотя они выглядят уже немного не так. Да и с развитием книгопечатания появилось много различных шрифтов как для букв, так и для цифр. Но в школах России учат писать всех детей одинаково.

Вот такая история цифр и чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют во всем мире.
Как мир учился считать
Цифры и числа – это разные понятия. В обиходе мы их путаем, но существенная разница в сути слов от этого не исчезла. Цифра служит для условного обозначения числа. Число выражает количественную характеристику в цифрах, и представляет собой более обобщенное понятие.
Если проанализировать, какими были первые цифры, можно увидеть обширную историю культуры отдельного народа. Составление обозначений для чисел потребовало более высокого интеллектуального уровня. Поэтому наши предки оставляли тысячи зарубок на твердых материалах. Столько, сколько требовалось. Так, наивно, но достоверно, заполнялись древние отчетные документы, «чеки» и т.п. Первые цифры представляли собой примитивные засечки и значки.

Пример древних чисел и цифр
Генезис цифр останется для ученых неизведанной Марианской впадиной. Витиеватая история возникновения вызывает замешательство. Точно известно, что первые попытки письменной фиксации цифр были в Египте и Месопотамии: найденные древние математические записи тому свидетельство. Эти государства располагались далеко друг от друга, письменность и культура в каждом из них уникальна.
В Древнем Египте сформировалось скорописное иероглифическое письмо, месопотамские писцы использовали клинопись. Поэтому египетские первые цифры своей формой передавали природу всех окружающих предметов: животные, растения, предметы быта и т.д. Папирус Ринда (1650 г. до н.э.) и папирус Голенищева (1850 г. до н.э.) – числовые древнеегипетские документы — свидетельствуют о высоком культурном развитии народа. Месопотамская клинопись запечатлена на глиняных табличках, на которых цифры представлены небольшими клиньями, повернутыми в разные стороны соответственно своему значению.
И в египетских, и в месопотамских системах счисления есть цифры от 1 до 10, особые метки для обозначения десятков, сотен и тысяч, и ноль, который обозначали выделенным пустым местом.
В иероглифах все проще. Число 100 выглядело почти как арабская цифра 9, но египтяне назвали ее лотосом. Далее все аналогично — 200 – 2 «лотоса», 300 – 3 и т.д.

Египетские числа и цифры
Вы заметили, что в древнем Египте с самого начала сформировалась десятичная система? Однако Месопотамия все же превзошла Египет, когда на ее территории обрел независимость и возвысился Вавилон. Там вырастала отдельная культура, вскормленная достижениями соседних завоеванных государств.
Достижение Вавилона
Числа древнего Вавилона мало отличались от месопотамских: те же клиновидные знаки служили для обозначения единиц — ˅, и десятков — ˃. Комбинация этих знаков применялась для обозначения чисел 11-59. Число 60 в письме выглядело как зеркальное отражение буквы «Г». 70 – Г˃, 80 — Г˃˃ и так далее, принцип ясен, клинопись не отличается гениальностью.
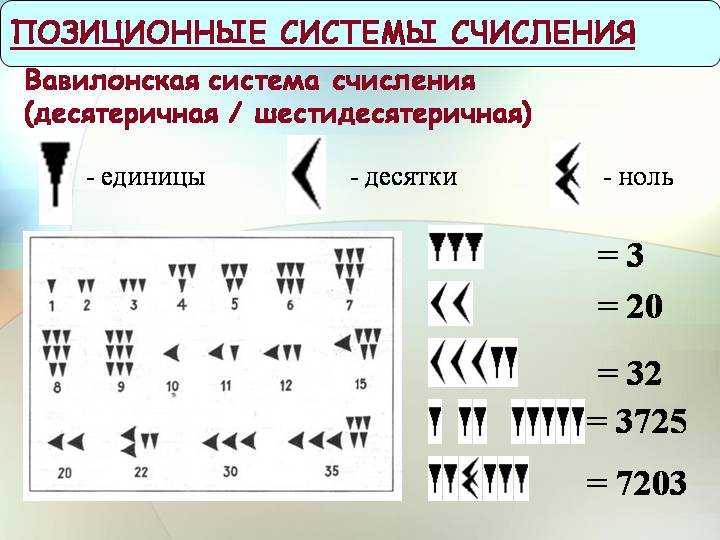
Вавилонская система счисления
Основная ценность заключается в том, что один и тот же знак – обратите внимание – в зависимости от того, где он расположен в записи числа, имеет разное значение. Речь идет о поместном размещении знаков в системе счисления
Те же клиновидные знаки, указанные в разных разрядах, обладают разной значимостью. Поэтому Вавилонскую систему счисления с нулем принято называть позиционной. Математики могут с этим поспорить, потому что не найдено ни одного источника, в которой ноль располагался бы в конце числовой записи, что говорит об относительной позиционности.
Вавилонская система стала своеобразным трамплином, с которого человечество совершило прыжок на новый этап своего развития. Идея со временем попала в руки индусов. Они внесли свои коррективы, усовершенствовав систему счисления. Переняли идею итальянские торговцы, которые привезли ее в Европу вместе с товаром. Позиционная система счисления облетела весь мир, обогатив своим появлением не только математические науки, но и современный счет.
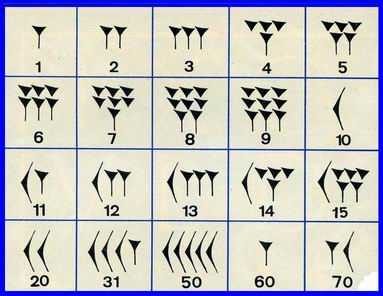
Знаете, откуда взялось деление часа на 60 минут, а минут – на 60 секунд? Из рассмотренной выше шестидесятеричной системы чисел. Взгляните, как обозначали числа древние вавилоняне, и в клиновидных значках увидите сакральный смысл современного, привычного для всех счисления.
«Биография» арабской цифры
История цифры 1.
Не только первая цифра в ряду, но и символ единства, совершенной целостности, как бог или космос. Смысл числительного «первый» семантически связано с именем Адама («первый человек»), а также с именами мифических персонажей Атум (созвучно со словом «атом», а мы знаем, что он неделимый), Один (от сканд. «первый», «верховный», «главенствующий»). Чувствуется фонетическое подобие слова «один» с «ЕДИНый», «жАДИНа». Улавливаете сходство?

История цифры 2
В названии цифры чувствуется парность, бинарное противопоставление, антонимичность, дуальность, четность. 2 – это защита от небытия и одиночества, противостояние единому. Вспомним, что Адам значит «первый», но после него не землю пришла Ева, она была «вторая». Ева значит «дева», а поскольку в древней Руси буквы «о» и «е» отсутствовали, то слово «дева» в письменном варианте выглядело как «дъва». Учитывая глубокую религиозную приверженность наших предков, имя «два» могло произойти из христианской мифологии.

История цифры 3
Недаром китайский цифровой ряд начинается с «тройки». Это совершенное число, за которым стоит ряд русских традиций – трижды постучать по дереву, трижды произнести «аминь» по окончанию молитвы, бог в православной вере существует в трех ипостасях. Цифра 3 обозначает крайнюю степень какой-либо характеристики. Например, «треклятый», «трисвятый». «Тройка» пишется практически одинаково с буквой «з», с которой начинается слово «земля». Как одна из стихий (1 – огонь, 2 – вода), земля вполне может оказаться третьей.
История цифры 4
Сравните русское слово «веер» с немецким словом «vier» («четыре»). Четвертая стихия – ветер — прячется под «четверкой». Кроме того, это четное число, «четыр». Оттуда и название.

История цифры 5
Одна из важнейших характеристик микро- и макрокосма. Ничего загадочного в этом нет. Вспомните, сколько у нас чувств, сколько классов животных, сколько элементов в буддийских упанишадах? Их пять. Цифра 5 находится у истоков навыков счета. В древней Руси считали «на пятках», то есть на пальцах руки. Выражение «знать, как пять своих пальцев», родом из той эпохи.

История цифры 6
На Руси цифру записывали под буквой «зело», пока не были введены арабские цифры. Сравните слова «зело» и «зло». Ведь 666 – три «зело» — обозначает абсолютное зло, треклятое (см. историю цифры 3).

История цифры 7
Цифра 7 начертанием и произношением сходна с латинской буквой Z («zet»). «Семь» созвучно с «земь», то есть «опора», «центр».

Сразу слышится «осемь», т.е. «ось». Цифра 8 напоминает букву «В», с которой начинается ее буквенная запись.

История цифры 9
Мы слышим троекратное повторение триады. «Девятка» — это обобщение всего цифрового ряда и ее превосходство одновременно.

Зная историю возникновения чисел, вы будете смотреть на них через призму своих знаний, будучи осведомленным о том смысле, который они таят под своим начертанием. Может, вы интуитивно догадывались об этих смыслах?
3.1 Древнеегипетская десятичная
Примерно в третьем тысячелетии до нашей эры древние
египтяне придумали свою числовую систему, в которой для обозначения ключевых
чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции
сложения. Система счисления Древнего Египта является десятичной, но
непозиционной и аддитивной.
|
1. Как и большинство людей |
|
|
Если палочек нужно изобразить несколько, то их изображали |
|
|
10. Такими путами египтяне |
|
|
Если нужно изобразить несколько десятков, то иероглиф |
|
|
100. Это мерная веревка, |
|
|
1 000. Вы когда-нибудь |
|
|
10 000. «В |
|
|
100 000. Это головастик. |
|
|
1 000 000. Увидев |
|
|
10 000 000. Египтяне |
Записывались цифры числа начиная с больших значений и
заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не
было, то переходили к следующему разряду.
— 1205, — 1 023 029
Попробуйте сложить эти два числа, зная, что более 9
одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с
этой системой нужен специальный человек. Обычному человеку это не под силу.
Характеристики чисел
Числа — это абстрактные математические объекты, которые играют ключевую роль в математических вычислениях и науках.
Характеристики чисел — это свойства, которые могут быть присвоены числам в соответствии с их определениями. Некоторые из характеристик чисел:
- Натуральные числа: положительные целые числа, которые начинаются с единицы и продолжаются бесконечно далее. Они используются для подсчета предметов и количества.
- Целые числа: все натуральные числа включая ноль и все отрицательные значения. Они используются для описания положительных и отрицательных значений, таких как температура и долги.
- Рациональные числа: числа, которые могут быть представлены в виде дроби, где верхняя и нижняя части представлены числами из целых чисел. Они используются для описания отношений и долей.
- Иррациональные числа: числа, которые не могут быть представлены в виде дроби. Они используются в математических вычислениях, где необходима высокая точность.
- Вещественные числа: числа, которые могут быть представлены в виде десятичных дробей. Они используются в математических вычислениях, где необходима высокая точность и значения могут быть положительными или отрицательными.
Характеристики чисел помогают ученым и математикам определить, какие операции можно выполнять с числами, какие свойства чисел можно использовать для решения задач и какие числа нужны для определенных задач.
ХарактеристикаПримеры чисел
| Натуральные числа | 1, 2, 3, 4, 5, … |
| Целые числа | -3, -2, -1, 0, 1, 2, 3, … |
| Рациональные числа | 1/2, 3/4, -1/3, 2/5, 0.75 |
| Иррациональные числа | √2, π, ℂ |
| Вещественные числа | -3.14, -0.5, 0, 0.5, 3.14 |
Часть 1. Теория.
Общеизвестна теория, описывающая возможный способ создания арабских цифр. Согласно ей каждая цифра содержит в своём написании соответствующее количество углов: цифра один содержит в своём написании один угол, цифра два содержит два угла и т.д. до девятки, которая содержит соответственно девять углов.
 |
Некоторые исследователи полагают, что именно такое соответствие углов (на рисунке выше) легло в основу написания современных цифр.
Однако, эта теория вызывает несколько вопросов. Почему двойка в данном исполнении больше похожа на семёрку, а семёрка на двойку?
Также у единицы изначально не было углов. Она изображалась как одна вертикальная черта. Это можно увидеть на картине Дюрера в магическом квадрате:
Ещё остаётся совершенно непонятным, почему эти цифры были названы арабскими. Нам известны настоящие арабские цифры, они показаны на рисунке в верхнем ряду:
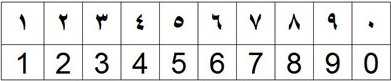 |
Как мы видим, арабская вязь совершенно не соответствует форме написания современных цифр. То же можно сказать и про индийские, и про китайские, и про любые другие, якобы древние, цифры.
Я не буду утруждать читателей анализом всех теорий и фантазий о происхождении современных цифр и сразу перейду к делу. Моя теория заключается в том, что современные цифры были созданы
во-первых: из букв только русского алфавита,
во-вторых: из первой буквы русского названия каждой цифры (кроме единицы, тут случай особый).
Такой путь создания цифр объясняется тем, что из-за высокой цены пергамента некоторые писари сокращали текст до первой буквы каждого слова. Это общеизвестно. Но, чтобы не перепутать обычные слова с числами, пришлось как-то видоизменять те буквы, которые обозначали числа.
2.4 Основание системы счисления
Основание системы счисления – это число, на основе которого
ведется счет. Например, если основание системы счисления равно десяти, то
минимальная счетная группа этой системы счисления равна десяти, это значит,
что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при
этом запоминаем число десятков. В нашей «арабской» системе основанием является
число десять. Есть системы счисления и с другим основанием. Это такие системы
счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.
Десятеричная и пятеричная система возникла от того факта,
что на одной руке человека пять пальцев, на обоих руках 10 пальцев.
Так проще считать. Если добавить пальцы и на ногах, то будет
понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже
связано со счетом на пальцах. Считали большой палец руки и фаланги остальных
четырех пальцев.
Если двенадцать умножить на пять получим шестидесятеричную
систему. Например, на одной руке загибаем пальцы, пока не получим, что отсчитано,
пять штук, а на другой руке прикосновением большого пальца к суставам остальных
четырех указываем количество этих пятерок.
В некоторых системах счисления используются для обозначения
цифр буквы, такие системы счисления называются алфавитными.
Итак, бывают непозиционные (аддитивные) и позиционные (мультипликативные),
пятеричные, десятичные, двенадцатеричные, двадцатеричные, шестидесятеричные и
алфавитные системы счисления.
Вначале рассмотрим непозиционные (аддитивные) системы
счисления.
Откуда взялись современные цифры?
Заслуга изобретения современных цифр (а именно их можно считать настоящими цифрами) принадлежит индусам. В пятом веке нашей эры они сделали важнейшее открытие: ввели в математический обиход понятие ноля и придумали для него знак – пустоту, обведенную в кружок. Насколько открытие ноля было важным, говорит тот факт, что в переводе с арабского само слово «Сыфр» (от которого произошло наше «цифра») обозначает именно ноль. Остальные цифры от 1 до 9 индийцы записывали с помощью простейших символов, похожих на те, которыми мы пользуемся сейчас.
Индусы стали представлять числа позиционным способом, когда число десятков, сотен, тысяч и других разрядов обозначается одной цифрой, стоящей на определенной позиции. Эту традицию они переняли у вавилонян. Стало возможным не просто записывать любые числа от нуля до бесконечности, но и проводить с ними математические операции.
А как индийские цифры попали в Европу и почему мы называем их арабскими? Арабы тесно контактировали с индийцами, вели оживленную торговлю. Кроме того, в арабских странах того времени активно развивались науки, культура и бизнес, а для этого было совершенно необходимо заниматься математикой. Арабы восприняли индийские цифры, начали ими пользоваться.
Известно имя человека, который впервые применил десятичную позиционную запись чисел по индийской методике и популяризировал данную идею в арабском мире. Это был персидский ученый Мухаммед ибн Муса аль-Хорезми, написавший свой знаменитый трактат по арифметике. В книге он изложил основы индийского счета и цифровой записи.
Это произошло в 9-м веке нашей эры. Новая система быстро распространилась на Ближнем Востоке, а в 10-13 веках попала и в Европу. В европейских странах арабские цифры изначально использовались при чеканке монет, затем – при нумерации страниц в книгах, в документах и т.д. Арабская система цифровой записи позволила человечеству сделать огромный скачок в науке, экономике, образовании. Эту систему способен усвоить любой дошкольник, она стала привычной, и мы редко задумываемся о том, что когда-то для записи больших чисел людям приходилось рисовать множество палочек или изображать на папирусе кошку!
Арабская система цифровой записи позволила человечеству сделать огромный скачок в науке, экономике, образовании. Эту систему способен усвоить любой дошкольник, она стала привычной, и мы редко задумываемся о том, что когда-то для записи больших чисел людям приходилось рисовать множество палочек или изображать на папирусе кошку!
Индия.[]
Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую.
Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления. Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чисел). Здесь мы впервые встречаемся с элементами современной системы счисления: индийская система была десятичной, цифровой и позиционной. При желании можно даже усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.
Напомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон. Однако происхождение индийского символа для нуля окутано тайной, так как первое достоверное свидетельство его появления в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не включили в свои системы счисления десятичные дроби, но именно индийцам мы обязаны современной системой записи обыкновенных дробей с числителем, расположенным над знаменателем (но без горизонтальной черты, отделяющей числитель от знаменателя).
Клинопись.
Клинописное письмо
Но человечество развивалось, хозяйство увеличивалось, усложнялись и подсчеты. Появилась потребность в записи чисел. Ведь на память невозможно упомнить, сколько в стаде голов скота, сколько мешков пшеницы у тебя лежит, а сколько потратили, сколько посадили и какой собрали урожай. И вот примерно в V веке до нашей эры появились первые цифры.
Говорят, что первые числа изобрели шумеры, народ, живший на территории Южного Междуречья Тигра и Евфрата, современного Ирака примерно в IV-III тысячелетии до н.э. Шумеры, кстати, очень интересный народ. Огромное количество изобретений, известных сейчас, были впервые использованы ими. Например, постельное белье, обожженный кирпич, колесо.
Шумеры изобрели и так называемое клинописное письмо или клинопись. На глиняных табличках рисовались различные символы в виде клиньев. Цивилизация шумеров была очень развита для тех времен. В их города жили торговцы, ремесленники. Для счета применялись сначала глиняные фишки различной формы. Со временем на них стали делать пометки, которые обозначали количество и вид того, что считали. Например, две козы. Но два мешка писали совершенно по-другому. То есть они описывали количество конкретных объектов и не выделяли отдельно цифру.
После шумеров на этих землях обосновались вавилоняне. Они переняли систему счисления шумеров. Египтяне тоже пользовались похожей системой счета.
Но все-таки подобный способ записи чисел не идеален и с развитием человечества развивалась и запись чисел.
Первобытный счет
Изначально люди использовали засечки. Их выполняли на мягком материале при помощи палочки или вырезали. Одна засечка соответствовала числу 1, две – 2 и так далее. Стоит отметить, что в древнейших документах, которые сохранились, число засечек отвечало тому числу, которое требовалось выразить. Прошло много веков, и люди поняли, что числам требуется присвоить разряды. Благодаря этому крупные величины удалось обозначать отдельными знаками. Это сделало запись намного проще.
Бытует мнение, что впервые числовые обозначения были придуманы в Древнем Египте и Вавилоне. Египтяне создали иероглифическое письмо. При этом числа обозначали черточками. Для разрядов же применялись особые символы. Начиная с сотни, это был стилизованный рисунок священного египетского животного – кошки.
https://youtube.com/watch?v=egwNhy4KGZA
Большой прорыв в обозначении чисел принадлежит древним вавилонянам. Они придумали позиционную запись. При этом в последовательности имел значение знак. В Вавилоне применяли 60-ричную систему счисления, которая используется и сегодня для определения времени. Так, час делится на 60 минут, а минута, в свою очередь, – на 60 секунд. Впоследствии появились римские и арабские цифры.
3.6 Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной
системой для перевода священных библейских книг для славян греческими монахами
братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое
распространение в связи с тем, что имела полное сходство с греческой записью
чисел. До XVII века эта форма записи чисел была официальной на территории
современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии.
До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к
меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед
десятком:
Читаем дословно «четырнадцать» — «четыре и
десять». Как слышим, так и пишем: не 10+4, а 4+10, — четыре и десять.
Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в
ней используется только сложение:
=
800+60+3
Для того чтобы не перепутать буквы и цифры, использовались
титла — горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались
специальные значки, которые дорисовывались к букве. Так образовывались числа:
|
Тысяча |
1000 |
|
|
Тьма |
10 |
|
|
Легион |
100 |
|
|
Леодр |
1 000 |
|
|
Ворон |
10 000 |
|
|
Колода |
100 000 |
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I
в Россию из Европы не пришла позиционная десятичная система счисления.
2.3 Позиционные и непозиционные системы счисления
Системы счисления бывают непозиционными (аддитивными) и
позиционными (мультипликативными).
Чтобы разобраться в этом рассмотрим для примера нашу
«арабскую» систему счисления. Например, число 3333 – три тысячи триста тридцать
три. Здесь каждая цифра «3» в зависимости от того, в каком месте находиться
обозначает свое число. Первая тройка слева, это три тысячи, вторая, три сотни,
третья – три десятка, четвертая – три единицы. Т.е. это позиционная система. В
таких же системах значение каждой цифры, зависит от ее положения (места,
позиции) в записи числа. В непозиционных системах значение каждой цифры не
зависит от ее положения (места, позиции) в записи числа.
Число 3333 можно представить в таком виде 3×1000 + 3×100 + 3×10 + 3. Т.е. для
представления этого числа используется умножение (по-английски multiplication), отсюда название этой системы — мультипликативная.
В непозиционных же системах для представления числа
используется сложение всех цифр, по-английски сложение – add.
Поэтому другое название этих систем — аддитивные.
Видео по теме:
Вопрос-ответ:
Кто изобрел цифры?
Цифры были созданы в разных культурах по всему миру. Они развивались на протяжении тысячелетий, и не были изобретены конкретным человеком в определенный момент времени.
Какие культуры внесли вклад в развитие цифр?
Цифры были разработаны и использовались разными культурами, включая Индию, Ближний Восток, Китай и древнюю Аравию. Каждая культура развивала свои собственные системы цифр.
Какие математики помогли в развитии цифр?
Многие математики по всему миру внесли свой вклад в развитие цифр, в том числе Леонардо Фибоначчи, Бхаскарачарья, Аль-Хорезми и т.д.
Какие типы цифр используются в математике?
Существуют два основных типа цифр в математике: арабские и римские. Арабские цифры — это цифры 0-9, они используются во всем мире для записи чисел. Римские цифры — это символы I, V, X, L, C, D, M, использующиеся до сих пор, преимущественно для указания порядка.
Как цифры влияют на развитие общества?
Цифры дали человечеству мощный инструмент для описания и измерения мира, имеют большое значение во всех областях человеческой деятельности, таких как наука, технология, финансы, экономика и т.д.
Как развивались цифры в России?
В России в древности использовались цифры абугидного типа, а позже стали использовать кириллические цифры, которые использовались до середины XIX века. Затем Россия переключилась на арабские цифры.
Как современные технологии влияют на использование цифр?
Современные технологии, такие как компьютеры и мобильные устройства, значительно упростили использование цифр в нашей повседневной жизни. Они помогают нам выполнять математические операции, хранить и анализировать данные и т.д.
Современные технологии и цифры

Современные технологии не только облегчают нашу жизнь, но и связаны с использованием цифр и математики. От обычных приложений для смартфонов до сложных алгоритмов искусственного интеллекта — все это невозможно без цифр и математических формул.
Одно из самых быстрорастущих направлений современной науки — это Big Data и Data Science. Каждый день мы создаем огромный объем данных, и чтобы понимать их, мы используем цифры и математику. Специалисты в этой области разрабатывают алгоритмы для обработки и анализа данных, используя такие инструменты, как Python, R и SQL.
Цифры также играют большую роль в современных финансовых технологиях. Трейдинговые алгоритмы, созданные на основе мыслительных процессов, используют математические модели для принятия решений о торговле акциями и другими видами инвестиций.
В области криптографии цифры играют ключевую роль. С использованием математических алгоритмов были созданы шифры и системы шифрования, которые защищают наши личные данные в Интернете от злоумышленников.
Таким образом, современные технологии и цифры тесно связаны друг с другом. Это открывает новые возможности и вызовы в области науки и технологий.
Будущее цифр в математике
Цифры являются основой математики и без них невозможно представить эту науку. Сегодняшние цифры используют десятичную систему счисления и существуют уже более 2000 лет. Однако, в будущем это может измениться.
С появлением компьютеров и новых технологий, появляется возможность использования других систем счисления в математике. Например, двоичная система счисления широко используется в компьютерной науке. Она позволяет уменьшить размер хранимых данных и ускорить вычисления. В общей математике также может появиться необходимость использования других систем счисления, особенно при работе с большими числами.
Кроме того, с развитием искусственного интеллекта и машинного обучения, цифры уже не только служат инструментом для проведения вычислений, но и могут генерироваться и анализироваться самими компьютерами. Это может привести к появлению новых математических объектов, которые в настоящее время еще не известны.
Также в будущем может измениться способ записи цифр. Например, появление квантовых компьютеров, которые могут работать с квантовыми битами, может привести к созданию новых цифр и нового способа их записи. Это может привести к изменению математических формул и алгоритмов, которые мы используем сейчас.
В целом, будущее цифр в математике связано с развитием технологий и новыми открытиями в науке. Возможно, мы столкнемся с самыми неожиданными и удивительными изменениями, касающимися цифр и их роли в математике.
Покорение Европы
В Средневековье европейцы пользовались римским исчислением, хотя контактировали с арабскими и африканскими странами и наверняка слышали сообщения на тему арабских цифр.
В своем нынешнем написании они появились в североафриканском городе Биджан, что недалеко от Алжира. В этом заслуга знаменитого математика Леонардо Пизанского, больше известного под псевдонимом Фибоначчи. Он является автором современной цифровой системы и во многом способствовал ее популяризации и распространению в мире.
Европейцев с новыми числовыми знаками познакомил другой ученый, Герберт Орильякский. Это произошло в конце X столетия в Испании. Европейцы сопротивлялись и долго не принимали «ноу-хау».

В повседневности ими почти никто не пользовался, хотя студенты в университетах изучали арабскую систему исчисления. В чем причина бытовой подозрительности граждан?
Объяснение простое – европейцев смущала легкость написания символов и возможность быстро исправить 1 на 7, приписать второе число спереди или сзади. А это уже — высокий риск махинаций. Власти Флоренции дошли до того, что запретили чиновникам и горожанам использовать индийский счет на работе и в быту – это произошло в 1299 году. Европейцам потребовалось больше полутора столетий, чтобы оценить его преимущества и отказаться от римской системы.
Арабские цифры.
Арабские цифры
В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
Запись цифры по числу углов
Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время.
Математик Мухаммед Аль-Хорезми в IX веке составил руководство об индийской нумерации. Оно в XII веке попало в Европу и эта система счисления получило очень широкое распространение. Интересно, но именно из-за того, что к нам эти цифры пришли от арабов, мы их называем арабскими, а не индийскими.
Кстати, и само слово «цифра» — арабского происхождения. Арабы перевели индийское «сунья» и получилось «цифр».
Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей.
Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы:
Современные арабские цифры
Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.
Вам также может быть интересно:






























