Форматы лент
- Q4 / квадрофоническая катушка на катушку (1969)
- Quad-8 (Q8) / квадрофонический 8-трековый (1970)
Также были представлены квадрофонические системы на основе ленты, основанные на новом оборудовании, способном воспроизводить четыре дискретных канала. Все эти записи представляют собой дискретные записи 4-4-4, выпущенные в форматах катушки на катушку и 8-трековых картриджей . Для воспроизведения этих записей требовались специально разработанные четырехканальные машины. Они не совместимы со стереоплеерами.
Квадрафоническая лента с открытой катушкой (Q4)
Четыре канала катушки к катушке ленты блок из 1970 — х лет, один из немногих способов достижения дискретного звука четыре канала в домашних условиях
В этих системах все четыре доступных трека были записаны на ленту, идущую в одном направлении. Предварительно записанные 4-х канальные ленты с катушкой на катушку были записаны со скоростью 7 и 1/2 дюйма в секунду (IPS), что является самой высокой скоростью, используемой для бытовых катушечных машин. Для сравнения, стереокассеты с предварительно записанными катушками имеют 2 разные программы, каждая из которых работает в противоположном направлении. Многие стереокассеты были записаны только со скоростью 3 и 3/4 IPS, что составляет половину полной скорости. Более низкая скорость приводит к значительно худшему качеству звука.
Кассета с 8 дорожками Quadraphonic (Quad-8 и Q8)
В апреле 1970 года RCA Records анонсировала четырехканальную версию 8-дорожечной ленты , названную Quad-8 или Quadraphonic 8-Track Tape (позже сокращенную до Q8). В конце концов они появились в сентябре 1970 года. Были и автомобильные плееры, и домашние версии.
Формат был почти идентичен 8-трековому стерео, за исключением небольшой выемки в верхнем левом углу картриджа. Это дало сигнал квадрофоническому 8-трековому проигрывателю объединить нечетные треки в качестве аудиоканалов для программы 1, а четные треки в качестве каналов для программы 2. Формат не был обратно совместим со стерео или моно плеерами; хотя квадрофонические плееры воспроизводили 8-трековые стерео, воспроизведение квадрофонических кассет на стерео проигрывателях приводило к одновременному прослушиванию только половины каналов.
Последний выпуск в квадрофоническом 8-трековом формате был выпущен в 1978 году, хотя большинство из них перестали появляться к концу 1976 года.
Квадрат обладает симметрией относительно своих диагоналей
Одним из важных свойств квадрата является его симметрия относительно своих диагоналей. Квадрат имеет две диагонали: главную и побочную.
Главная диагональ квадрата соединяет противоположные вершины и делит фигуру на два равных треугольника.
Побочная диагональ квадрата соединяет другие две противоположные вершины и также делит фигуру на два равных треугольника.
Интересно, что при отражении квадрата относительно главной диагонали каждая точка сама себе соответствует. То есть, если взять точку A на квадрате и отразить ее относительно главной диагонали, получится точка A. Аналогично, при отражении относительно побочной диагонали, каждая точка также остается на своем месте.
Это свойство симметрии позволяет делать обобщения и решать задачи, связанные с квадратами. Например, если требуется доказать, что определенные углы квадрата равны, можно использовать симметрию относительно диагоналей.
📽️ Видео
Вписанная и описанная окружность — от bezbotvyСкачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Четырехугольники. Вебинар | МатематикаСкачать

Математика без Ху!ни. Определенные интегралы, часть 1.Скачать

Проектирование.Изображение фигур в пространстве.Часть 1.Скачать

Виды четырёхугольниковСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

Миникурс по геометрии. ЧетырехугольникиСкачать

Пространственные фигуры. Прямые и плоскости. 10 класс. Вебинар | МатематикаСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

тема 8 3 Параллельное проектирование и его свойстваСкачать
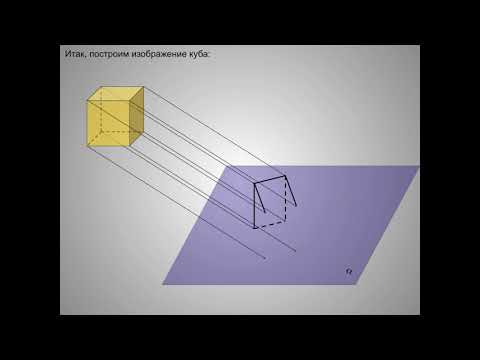
Занятие 1. Пространственные фигуры. Прямые и плоскости. Математика 10 классСкачать

Свойство и признак вписанного четырехугольникаСкачать

4D фигурыСкачать

#211. ГИПЕРКУБ и четвертое измерениеСкачать

Квадрат
Следующий вопрос из тех, что мы рассмотрим в этой публикации, – какой четырехугольник называется квадратом? Это фигура, обладающая равными сторонами и углами в девяносто градусов. Исходя из указанных выше параметров, она обладает всеми теми же свойствами, которыми обладают прямоугольник и ромб. Соответственно имеет также их признаки.
К особенностям квадрата можно отнести уникальные свойства линий, соединяющих его противоположные вершины и называемых диагоналями. Они имеют одну длину и пересекаются под прямым углом.
Прикладное значение квадрата сложно переоценить. Благодаря своей универсальности, простоте определения площади и размеров, эта фигура широко используется в качестве эталонной меры. Число возведенное во вторую степень устойчиво называется математиками квадратом. С помощью квадратных единиц измеряют площадь, осуществляют интеграцию и общие приближения размеров на плоскости. Широко эта геометрическая концепция используется в архитектуре и ландшафтном дизайне.
Современная символика квадрата: от геометрии до искусства
Квадрат – один из фундаментальных геометрических элементов, который обладает множеством символических значений. В современной символике квадрат используется для выражения идей симметрии, устойчивости, равенства и порядка.
Геометрические значения
Самое основное значение квадрата в символике – это его геометрическая форма. Как фигура с четырьмя прямыми и одинаковыми сторонами, квадрат ассоциируется с идеями симметрии и структурированности. Он может служить символом гармонии и уравновешенности в архитектуре и дизайне. Также квадрат используется в математических системах и геометрических расчетах в различных науках.
Символика в искусстве
Квадрат широко применяется в искусстве как символический элемент. В абстрактном искусстве, например, квадрат может выражать идею простоты и минимализма. Он может служить пространственным ориентиром или разделителем в композиции, создавая гармонию и структурированность. Картины с квадратными формами могут восприниматься как устойчивые и сбалансированные.
Символизм в культуре
Квадрат также имеет символическое значение в различных культурах и религиях. Например, в геральдике квадрат может служить символом честности и справедливости. В традиционных японских садах квадратные формы используются для выражения равновесия и порядка. В декоративном искусстве квадрат может символизировать структуру и гармонию всего мира.
Символическое значение цвета
Кроме геометрической формы, цвет квадрата также может иметь символическое значение. Например, черный квадрат может ассоциироваться с мистикой и тайнами, а красный квадрат – с энергией и страстью. Цвет квадрата может быть выбран в соответствии с желаемым эмоциональным или символическим эффектом.
Вывод
Символика квадрата является многообразной и применяется в различных областях, от геометрии до искусства. Квадрат символизирует идеи симметрии, структурированности, устойчивости и порядка. Он может служить основой для создания гармоничных композиций, а также иметь символическое значение в культуре и религии. Кроме геометрической формы, значимость квадрата может быть также связана с его цветом, создавая различные эмоциональные эффекты.
От стерео к квадро

В начале двадцатого столетия на регулярной основе в сфере записи стереозвука проводились различные эксперименты. Но применяемые технологии были не только очень сложными, но и дорогостоящими.
Интересно то, что первой стерео-аппаратурой, выпускающейся серийно, оказался магнитофон. Его изобрели намного позже после появления проигрывателя с грампластинками. Стереомагнитофоны первой стала производить фирма из Америки RCA в 1955 г. В 1958 г., спустя еще три года, было налажено производство стерео-грампластинок и, соответственно, проигрывателей.
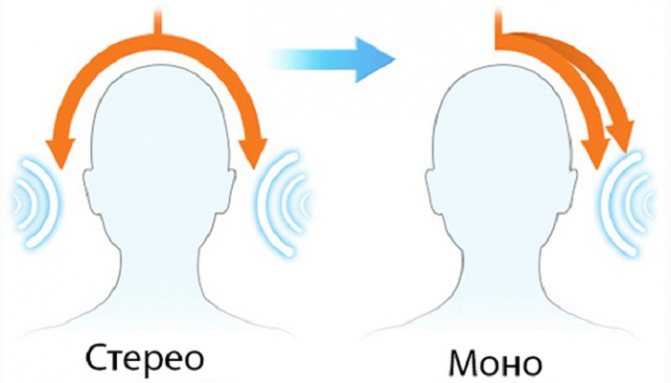
В течение почти десяти последующих лет моно и стерео существовали параллельно и даже не конкурировали. Моно считалась аппаратурой бюджетного класса и была доступной всем. Стерео имела более высокое качество, а значит и цену. Ее могли себе позволить люди с более высоким достатком.
К концу шестидесятых годов прошлого столетия ряд производителей пришел к выводу, что пора налаживать выпуск еще одного типа устройств – таких, которые бы воспроизводили квадро звук. Причиной принятия этого решения стало не слишком уж хорошее качество аппаратуры, а желание получить определенную прибыль. Создатели решили, что если стерео нашло своего потребителя, пусть и не сразу, то и с квадро ситуация будет аналогичной. Но на этой новинке заработать можно будет больше.

Чтобы делать квадро запись, необходимо наличие четырех каналов. Они есть и в стереомагнитофонах – два в одну и два в другую сторону. По большому счету, нужно слегка переделать обычный стереомагнитофон, чтобы он стал квадро. Ну а так как места для дополнительных двух каналов не было, создатели пошли на хитрость. Компании JVC (Япония) и RCA (США) разработали стандарт CD-4 – достаточно интересное решение. Его принцип заключается в том, что на каждый из каналов пластинки производится запись полосы частот 20 Гц-40 кГц. Полоса поделена на два фронтальных стереоканала с частотой 20 Гц-15 кГц. С помощью модуля на полосу с частотой 18 кГц до 45 кГц перенесли тыловые каналы (тоже стерео). Это FM-PM-SSBFM модуляционный тип.

В Columbia Records был разработан «Stereo Quadraphonic». Этот стандарт подразумевал запись на стерео-дорожки комбинированных данных, которые состоят из сигнала фронтальных и тыловых каналов (сдвиг на девяносто градусов). Не лучшее решение, так как межканальное затухание было только 3 Дб. Со временем, конечно, получилось повысить до 12 Дб, но и это не намного лучше. Плюс ко всему, появились сложности с декодированием после того, как комбинированный сигнал передастся по эфиру.
Древние народы и квадрат: первые символические значения
Квадрат – это одна из самых простых и универсальных геометрических форм, которая встречается в природе и создана человеком. Уже в древние времена, различные народы придавали квадрату особое символическое значение. В этой статье мы рассмотрим первые символические значения, которые были связаны с квадратом.
1. Устойчивость и стабильность.
Квадрат, в своей простоте и регулярности, символизировал устойчивость и стабильность. У древних народов, квадрат часто ассоциировался с основой, фундаментом и надежностью. Будучи самодостаточной формой, квадрат создавал ощущение надежности и порядка.
2. Четыре стороны света и баланс.
Во многих культурах, квадрат был символом четырех основных сторон света: востока, запада, севера и юга. Эта ассоциация отражала идею баланса и гармонии, которые присущи природным элементам и вселенной в целом. Квадрат также символизировал равновесие и уравновешенность в жизни человека.
3. Вселенная и космос.
У некоторых древних народов квадрат был ассоциирован с представлением о вселенной и космосе. Вертикальные и горизонтальные линии квадрата могли символизировать основные направления движения и регулярность звездных систем. Квадрат также мог служить моделью для построения земных и космических структур.
4. Защита и безопасность.
Еще одним символическим значением квадрата у древних народов была его связь с идеей защиты и безопасности. За счет своей устойчивости и закрытости, квадрат создавал ощущение защищенности и представлял собой символический убежище от внешних опасностей и злоупотреблений.
Таким образом, уже очень давно квадрат был не только геометрической формой, но и нес в себе глубокие символические значения для древних народов. В следующих статьях мы рассмотрим более развитые символические интерпретации и использования квадрата в различных культурах и эпохах.
Слайд 25Используемая литератураГ.П.Левитас «Современный урок математики. Методы преподавания». («Просвещение»; М., 2004 г.)Д.А.Пойя
«Как решать задачу». (журнал «Квантор», Львов.1998 г.)У.Д.Тайсмаханов «Создание проблемной ситуации» (журнал «Математика в школе», №5 1996 г.)М.Сканари «Избранные задачи». (газета «Математика». №5 2001 г.)Л.Н.Фридман. «Учитесь учиться математике». («Просвещение». М., 2000 г.)Газета «Математика». (2010-2011 г.)М.Е.Козина «Сборник элективных курсов. Математика.8-9 классы». («Учитель». Волгоград., 2006 г.)А.И.Азевич. «Двадцать уроков гармонии». (Москва, «Школа-Пресс», 2008 г.)Л.Э.Генденштейн «Математика. Наглядный справочник с примерами» (Москва. «ИЛЕКСА»., 2009 г.)Хрестоматия «Я познаю мир».Л.С.Атанасян. «Геометрия 7-9 классы».
Стерео наушники или с объемным звуком?
Ответ на этот вопрос довольно прост — лучше подойдут наушники со стерео преобразователями.
- Во-первых, они намного дешевле. И если пользователь планирует потратить на них много денег, они, безусловно, будут предлагать лучшее качество звука, чем сопоставимые эквиваленты 5.1 или 7.1.
- Во-вторых, объемный звук в наушниках — это скорее имитация. На многих форумах можно найти отзывы игроков о том, что традиционные модели намного лучше, а 5.1 или 7.1 — это просто маркетинговый трюк.
Выбирая наушники, стоит проверить их звучание, а также комфорт их расположения на голове. Это может стать решающим фактором при многочасовых игровых сессиях.
Преимущества багги над квадроциклами
Программы на «Квадроранчо» — это не офф-роуд, это прогулки на квадроциклах и багги по пересеченой местности с элементами офф-роуда. Данный формат не подразумевает гонок «на выживание», выезда на серьезное бездорожье и позволяет участвовать всем — и взрослым, и детям (в качестве пассажиров) одновременно, в любую пору года.
Учитывая эти особенности, опыт использования багги на протяжении нескольких сезонов показал их приемущества в сравнении с квадроциклами.
Руль
Багги — это маленький автомобиль, соответственно, руль для большинства пользователей — привычный, автомобильный. Это очень сильно влияет при поездках на длительные расстояния — не «забиваются» руки. Данный факт особенно важен для участников с небольшим опытом или без него. С таким рулем привычнее, удобнее и легче.
За «автомобильным» рулем в зимний период удобнее сидеть в теплых рукавицах, что не всегда удается на квадроцикле.
Безопасность
Багги более безопасны. У машины есть каркас безопасности. Багги шире квадроциклов, что в совокупности с автомобильной посадкой и, соответственно, низким центром тяжести минимизирует вероятность переворота при заносе.
Крыша
У багги есть крыша и экипаж более защищен от солнца, веток, внезапного дождя или снега.
Посадка side-by-side
Водительское и пассажирское сидения расположены рядом. Это очень удобно. Пассажиру не надо держатся за водителя и выглядывать из-за спины. У водителя и пассажира хорошая обзорность.
Дети
Парам с детьми удобно ехать на багги. Ребёнка можно пристегнуть ремнями безопасности к пассажирскому креслу, и он будет всегда под контролем. С детьми на багги безопаснее и удобнее.
Скорость
В формате багги и квадро сафари колонна на багги может ехать быстрее при том же уровне безопасности.
У багги и квадроциклов есть свои плюсы и минусы, выбрать на чем ехать можно исходя из погодных условий, формата катания и состава группы. Однозначного ответа на вопрос, что лучше, нет, потому что это концептуально разная техника.
С уверенностью можно утверждать только одно – один и тот же маршрут на багги и квадроцикле – два совершенно разных маршрута с другими эмоциями и впечатлениями!
История
Первыми машинами, использовавшимися для 4-канальной звукозаписи, были аналоговые катушечные магнитофоны. Они были разработаны для использования звукоинженерами в профессиональных студиях в 1950-х годах в Германии компанией Telefunken, а также компанией Ampex в США. Такие аппараты появились в некоторых европейских студиях электронной музыки к 1954 году, ранним примером была кассетная часть пьесы Карлхайнца Штокхаузена « Контакт» (1958–60). Однако, хотя для этой записи в студии использовалась четырехканальная технология, она никогда не была выпущена для публики в квадрофоническом звуке, только в стерео.
Ранние попытки воспроизвести четырехканальный звук для домашнего воспроизведения начались инженерами аудиолаборатории в 1960-х годах. Небольшое количество квадрофонических записей было представлено на американском потребительском рынке компанией Vanguard Records в июне 1969 года на катушечной ленте. Самая популярная среда , используемая для рынка записей общественности в течение 1970 — х годов был винил LP фонограф запись . Квадрафонические записи на 8-дорожечную ленту также были популярны в 1970-х годах, особенно среди энтузиастов автомобильного звука.
В 1970-х годах крупные производители электроники предлагали населению специализированные аппаратные системы для декодирования 4-канальных записей. Эти декодеры часто продавались как отдельные электронные компоненты. Декодеры также были доступны в качестве встроенных функций некоторых аудиоприемников или усилителей, продаваемых в 1970-х годах.
Во многих квадрофонических записях 1970-х использовались «матричные» технологии для кодирования и декодирования 4-канальной аудиоинформации на 2-канальном носителе, обычно LP. Плохая производительность декодирования ранних матричных форматов была основной причиной их исчезновения после появления улучшенных матричных систем. Более поздние матричные системы были основаны на работе Питера Шайбера . В его базовой формуле использовалась схема с фазовым сдвигом на 90 °, что позволило разработать улучшенные матричные системы 4-2-4, двумя основными лидерами которых были SQ от Columbia и QS Systems от Sansui.
Тремя наиболее популярными квадрофоническими форматами LP в 1970-х были SQ (стереоквадрафонический) , QS (обычный матричный) и CD-4 (совместимый дискретный 4) / квадрадиск .
Вместе с Шайбером и Мартином Уиллкоксом Джим Фосгейт разработал декодер Tate II 101 SQ, который создавал очень точное звуковое поле за счет использования усиления и эффекта Хааса для маскировки артефактов декодирования. В нем использовались заказные, собранные вручную и откалиброванные схемы с компонентами, отсортированными до 1%, для точной работы. Декодеры Sansui серии QSD и приемники серии QRX были очень хороши, они даже синтезировали лево-правое стерео в ⋂ подковообразную топологию. Однако все они появились слишком поздно и были слишком дороги или трудны для публичной покупки, чтобы спасти матричный квад.
К началу 2000-х более сложные «дискретные» многоканальные системы в основном заменили матричные технологии, обеспечивая более высокий уровень производительности и полную независимость каналов.
Сегодня программное обеспечение можно использовать вместо аппаратного декодирования. Современные программные алгоритмы способны обеспечить более точное декодирование, чем более ранние аппаратные технологии.
Все широко используемые сегодня многоканальные аудиосистемы являются цифровыми . Цифровое многоканальное аудио стало доступно для дома, начиная с появления фильмов с объемным звуком с использованием Dolby Digital и DTS в 1990-х годах. Наиболее распространенными цифровыми носителями, способными воспроизводить музыку с объемным звуком сегодня, являются Super Audio CD, DVD и Blu-ray. Все они способны воспроизводить аудио высокого разрешения по нескольким каналам.
История и символика квадрата: от древних времен до современности
Квадрат – это геометрическая фигура, у которой все стороны равны друг другу, а углы прямые. Квадрат имеет множество символических значений и ассоциаций, которые были частью различных культур и цивилизаций на протяжении многих веков.
Древний Египет: Квадрат символизировал стабильность и порядок. В древнем Египте квадрат был ассоциирован с идеей вечного и неизменного, что находило отражение в архитектуре и обрядах.
Древняя Греция: Квадрат был важной геометрической фигурой для древних греков. Они использовали квадрат как символ баланса, справедливости и гармонии
Квадрат также используется как основа для множества других геометрических форм и дизайнов, которые можно найти в античной греческой архитектуре и искусстве.
Средние века: В христианской символике квадрат был ассоциирован с идеей земли и материального мира, в отличие от небесного и духовного. Квадрат также служил символом четырех кардинальных направлений – север, юг, восток и запад.
Раннее Возрождение: В эпоху Возрождения квадрат получил новое значение, ассоциируясь с идеями гармонии, рациональности и равновесия. Квадрат стал одним из ключевых элементов геометрических композиций и рисунков, а также использовался в архитектуре и изобразительном искусстве.
Современность: В современном мире квадрат всё ещё используется как символ порядка, равновесия и степени. Он часто встречается в дизайне и логотипах, чтобы выразить простоту и симметрию. Квадрат также олицетворяет идею стабильности, безопасности и надежности, что делает его популярным выбором для различных брендов и организаций.
Примеры использования квадрата в мире дизайна и логотипов:
Пример 1
Пример 2
Итак, квадрат имеет множество значений и символических ассоциаций, которые привлекают к себе внимание с древних времен до наших дней. Этот простой геометрический символ продолжает влиять на нашу культуру и восприятие мира, а также оставаться популярным средством для выражения идей и концепций
Пространственный четырехугольник
Пространственный четырехугольник обладает рядом особенностей и свойств, которые отличают его от других геометрических фигур.
- Стороны: у пространственного четырехугольника есть четыре стороны, которые могут быть различной длины и формы.
- Углы: пространственный четырехугольник имеет четыре угла, каждый из которых может быть различной величины.
- Диагонали: пространственный четырехугольник имеет шесть диагоналей, которые соединяют вершины фигуры.
- Площадь: пространственный четырехугольник имеет площадь, которая определяется как половина векторного произведения векторов, образованных сторонами четырехугольника.
- Объем: пространственный четырехугольник имеет объем, который определяется как произведение площади основания и высоты фигуры.
Существуют различные виды пространственных четырехугольников, такие как тетраэдр, прямоугольный параллелепипед, ромбоэдр и другие. Каждый из них имеет свои уникальные свойства и характеристики.
Примером пространственного четырехугольника может служить тетраэдр, который состоит из четырех треугольных граней и четырех вершин. У каждой грани тетраэдра есть три стороны и три угла.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Главные виды квадроциклов
Существует несколько основных видов квадроциклов:
Спортивные квадроциклы. Это быстрые и маневренные транспортные средства, специально разработанные для соревнований и экстремального вождения. Они оснащены мощными двигателями и современными системами подвески, которые обеспечивают лучшую управляемость и повышенную проходимость.
Утилитарные квадроциклы. Эти квадроциклы предназначены для использования в сельском хозяйстве, лесном хозяйстве и других рабочих областях. У них практичные грузовые отсеки и специальные приспособления для перевозки грузов. Утилитарные квадроциклы обладают повышенной проходимостью и мощностью, чтобы справиться с тяжелыми условиями работы.
Рекреационные квадроциклы. Их также называют туристическими или охотничьими квадроциклами. Они предназначены для людей, которые ищут приключений на природе. Рекреационные квадроциклы имеют комфортное сиденье и удобные рукоятки для пассажиров. Они обладают хорошей маневренностью и отличными характеристиками, чтобы исследовать труднодоступные места и преодолевать различные препятствия.
Детские квадроциклы. Эта категория квадроциклов предназначена для детей. Они меньше и менее мощные, но все же обладают характеристиками, позволяющими детям получить удовольствие от вождения. Детские квадроциклы оснащены специальными механизмами для безопасности и контроля скорости, чтобы предотвратить травмы и обеспечить безопасное вождение.
Каждый из этих видов квадроциклов имеет свой уникальный набор характеристик и предназначение. Выбор конкретного типа зависит от целей и потребностей каждого владельца.
Что нужно игрокам?
Звук, вопреки внешнему виду, чрезвычайно важен во многих играх. В основном это относится к многопользовательским играм, в которых пользователи соревнуются с другими игроками. Например, в «Counter-Strike: Global Offensive» играть без наушников практически бессмысленно. Без них игрок не услышит приближающегося врага и не зафиксируем момент начала обезвреживания бомбы. Но то же самое касается «Battlefield» или «Call of Duty». Тем не менее все эти игры довольно хорошо справляются с воспроизведением объемного звука на обычных стереонаушниках. Создатели позаботились о соответствующих решениях, благодаря которым можно отлично слышать, с какой стороны приближается соперник. Но разве с наушниками 5.1 или 7.1 не было бы еще проще?
Сколько прямых углов в квадрате?
По диагоналям: Если диагонали четырехугольника равны, перпендикулярны и делятся пополам в точке пересечения, то это квадрат. По ромбу: Если в ромбе все углы прямые, то это квадрат. По прямоугольнику: Если в прямоугольнике все стороны равны, то это квадрат.
Одна диагональ разделяет квадрат на два равнобедренных треугольника, обе — на четыре. Что такое квадрат, мы с вами выяснили. Давайте подробнее рассмотрим детали, ведь фигура квадрат самый симметричный четырехугольник. У него пять осей симметрии, причем одна четвертого порядка проходит через центр и является перпендикуляром к плоскости самого квадрата, а четыре другие — оси симметрии второго порядка, две из них параллельны сторонам, а еще две проходят через диагонали квадрата. Способы построения квадрата Исходя из определений, кажется, что нет ничего проще, чем построить правильный квадрат. Это так, но при условии, что у вас есть все измерительные инструменты. А если чего-то нет в наличии? Давайте рассмотрим существующие способы, которые помогут нам построить эту фигуру. Измерительная линейка и угольник — это основные инструменты, при помощи которых наиболее просто можно построить квадрат. Сначала отметьте точку, допустим А, от нее мы построим основание квадрата. С помощью линейки отложите от нее вправо расстояние, равное длине стороны, допустим 30 мм, и поставьте точку Б. Теперь от обеих точек, воспользовавшись угольником, проведите вверх перпендикуляры по 30 мм каждый. На концах перпендикуляров ставим точки В и Г, которые соединяем между собой, пользуясь линейкой — все, квадрат АБВГ со стороной 30 мм готов! С помощью линейки и транспортира тоже довольно легко построить квадрат. Начните, как и в предыдущем случае с точки, допустим Н, от нее отложите горизонтальный отрезок, например 50 мм. Поставьте точку О. Теперь центр транспортира соедините с точкой Н, поставьте отметку у величины угла 900, через нее и точку Н постройте вертикальный отрезок 50 мм, на его конце поставьте точку П. Далее подобным образом постройте третий отрезок от точки О через угол 900, равный 50 мм, пусть он заканчивается точкой Р. Соедините точки П и Р. У вас получился квадрат НОРП с длиной стороны 50 мм. Можно построить квадрат, пользуясь только циркулем и линейкой. Если вам важен размер квадрата и известна длина стороны, то понадобится еще и калькулятор. Итак, ставьте первую точку Е — это будет она из вершин квадрата. Далее укажите место, где будет находится противоположная вершина Ж, то есть постойте диагональ ЕЖ вашей фигуры. После того как вы узнаете длину диагонали, постройте отрезок ЕЖ этой величины. Из точки Е с помощью циркуля в направлении точки Ж проведите полукруг радиусом ЕЖ. И наоборот, из точки Ж — полукруг в сторону точки Е, радиусом ЖЕ. Через точки пересечения этих полукругов, пользуясь линейкой, постройте отрезок ЗИ. ЕЖ и ЗИ пересекаются под прямым углом и являются диагоналями будущего квадрата. Еще есть возможность построить квадрат с помощью одной линейки. Это участок плоскости, ограниченный пересекающимися отрезками линиями, лучами. Следовательно, мы можем построить квадрат по координатам его вершин. Сначала начертите оси координат. Стороны квадрата могут лежать на них, или центр пересечения диагоналей будет совпадать с точкой начала координат — это зависит от вашего желания или условий задачи. Возможно, ваша фигура будет отстоять от осей на некотором расстоянии. В любом случае, сначала отмечаете по числовым значениям произвольно или условно две точки, тогда вам будет известна длина стороны квадрата. Теперь можно вычислить координаты оставшихся двух вершин, помня, что стороны квадрата равны и между собой попарно параллельны. Последний шаг — соединить все точки последовательно между собой с помощью линейки. Какие бывают квадраты? Квадрат — фигура четко определенная и жестко ограниченная своими определениями, поэтому виды квадратов не отличаются многообразием. В Неевклидовой геометрии квадрат воспринимается более широко — это четырехугольник с равными сторонами и углами, но градус углов не задан. Это значит, что углы могут быть и по 120 градусов «выпуклый» квадрат и, например, по 72 градуса «вогнутый» квадрат. Если вы спросите, что такое квадрат, у геометра или информатика, вам ответят, что — это полный или планарный граф графы с К1 по К4. И это абсолютно справедливо.
Разбиение квадрата сеткой одинаковых более мелких квадратов также приводит к множеству проблем, используемых, в частности, в теории латинских и греко-латинских квадратов , магических квадратов , в игре судоку.
Свойства
Пространственные четырехугольники обладают рядом уникальных свойств.
1. Пространственный четырехугольник имеет четыре вершины, которые образуют четыре угла.
2. Все стороны пространственного четырехугольника являются отрезками прямых линий, которые соединяют вершины четырехугольника.
3. Сумма всех углов в пространственном четырехугольнике равна 360 градусов.
4. Пространственный четырехугольник может быть выпуклым или невыпуклым. Выпуклый четырехугольник имеет все углы меньше 180 градусов, в то время как невыпуклый четырехугольник имеет как минимум один угол больше 180 градусов.
5. Сумма длин двух противоположных сторон пространственного четырехугольника всегда больше суммы длин двух других сторон.
6. Диагонали противоположных углов пространственного четырехугольника пересекаются в точке, которая называется точкой пересечения диагоналей.
7. Пространственные четырехугольники могут быть разделены на два треугольника при проведении одной из диагоналей.
8. Сумма длин двух противоположных сторон пространственного четырехугольника всегда больше длины диагонали.
Знание этих свойств позволяет более детально изучить и анализировать пространственные четырехугольники и их особенности.
Какие свойства имеет пространственный четырехугольник?
Во-первых, пространственный четырехугольник имеет четыре стороны, которые являются отрезками, соединяющими вершины этой фигуры. Каждая сторона пространственного четырехугольника определяется двумя вершинами.
Во-вторых, пространственный четырехугольник имеет четыре угла. Каждый угол образован двумя соседними сторонами пространственного четырехугольника.
В-третьих, пространственный четырехугольник может быть выпуклым или невыпуклым. Если все точки внутри пространственного четырехугольника лежат по одну сторону от плоскости, образованной его сторонами, то он называется выпуклым. В противном случае, если есть точки, лежащие по обе стороны плоскости, пространственный четырехугольник называется невыпуклым.
В-четвертых, пространственный четырехугольник может быть регулярным или нерегулярным. Регулярный пространственный четырехугольник имеет все стороны и углы одинаковой длины, тогда как нерегулярный пространственный четырехугольник имеет разные стороны и углы.
В-пятых, пространственный четырехугольник может иметь различные измерения. Может быть пространственный четырехугольник плоским, то есть все его вершины лежат в одной плоскости. Может быть также пространственный четырехугольник невыпуклым, когда он пересекает себя.
Также важно отметить, что пространственный четырехугольник может быть прямоугольным, когда он имеет четыре прямых угла. Он также может быть трапецией, ромбом, ромбоидом или квадратом, в зависимости от своих сторон и углов
Какие существуют виды пространственных четырехугольников?
Пространственные четырехугольники могут быть различных видов и иметь разнообразные свойства. Некоторые из наиболее распространенных видов пространственных четырехугольников:
- Прямоугольник — четырехугольник, у которого все углы равны 90 градусов. У прямоугольника противоположные стороны параллельны, а все его углы прямые.
- Квадрат — особый вид прямоугольника, у которого все стороны равны и все углы прямые. Квадрат является одновременно и прямоугольником.
- Ромб — четырехугольник, у которого все стороны равны. У ромба противоположные углы равны, но они не являются прямыми.
- Трапеция — четырехугольник, у которого две пары противоположных сторон параллельны. У трапеции нет равных углов, но два угла могут быть сумplementными, то есть их сумма составляет 180 градусов.
- Параллелограмм — четырехугольник, у которого противоположные стороны параллельны. У параллелограмма все углы прямые, или два зеркально-симметричными относительно центра или два сумplementными, то есть их сумма составляет 180 градусов.
Это лишь некоторые из возможных видов пространственных четырехугольников. В зависимости от свойств и соотношений сторон и углов, их может быть гораздо больше. Каждый вид четырехугольника имеет свои уникальные характеристики и применения в практических задачах.
Видео:Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

Четырехугольник с прямыми углами: название и свойства
Четырехугольник, у которого все углы прямые, называется прямоугольником. Это особый тип четырехугольника, который обладает рядом уникальных свойств.
Свойства прямоугольника:
- Все углы прямые. Прямые углы равны 90 градусам, что делает прямоугольник идеальной фигурой для построения и измерения прямых углов.
- Противоположные стороны прямоугольника равны по длине. Это означает, что две стороны параллельные и равные друг другу, а также две другие стороны параллельные и равные друг другу.
- Диагонали прямоугольника равны по длине и делят его пополам. Диагонали пересекаются в точке, которая является центром симметрии прямоугольника.
- Прямоугольник может быть разделен на два прямоугольных треугольника, каждый из которых имеет гипотенузу, параллельную одной из сторон прямоугольника.
- Периметр прямоугольника вычисляется по формуле P = 2a + 2b, где a и b — длины сторон прямоугольника.
- Площадь прямоугольника вычисляется по формуле S = a * b, где a и b — длины сторон прямоугольника.
Прямоугольник является одной из наиболее распространенных геометрических фигур и широко используется в архитектуре, инженерии, строительстве и других областях. Его уникальные свойства делают его важным инструментом для измерений и расчетов.






























