Квантиль распределения: определение
Медиана – это пример квантиля. Когда мы говорим о медиане, мы обычно имеем в виду 50-й процентный квантиль. На графике плотности распределения медиана является значением, которое делит площадь по обе стороны графика на две равные части.
Квантили широко используются в статистике и экономике. Они позволяют изучать распределение случайной величины и анализировать вероятности значений внутри этого распределения. Как правило, квантили используются для оценки риска и принятия решений на основе статистических данных.
Квантиль распределения: понятие и свойства
Как правило, квантили обозначаются буквой q, за которой следует уровень вероятности в процентном выражении. Например, если значению квантиля соответствует вероятность 0.25, то его обозначают как q25.
Основное свойство квантилей – это возрастание вероятности с ростом значения квантиля. Другими словами, чем больше значение квантиля, тем выше вероятность того, что случайная величина будет принимать значения меньше этого квантиля.
Также стоит отметить, что существуют различные типы квантилей. Например, медиана – это квантиль, который разделяет распределение на две равные части. Наиболее часто используются квантили, разделяющие распределение на четыре равные части (четвертили), пять равных частей (квинтили) или десять равных частей (децили).
| Тип квантиля | Обозначение | Количество частей |
|---|---|---|
| Медиана | q50 | 2 |
| Первый и третий квартили | q25, q75 | 4 |
| Пятая и девяностая децили | q5, q90 | 10 |
Знание квантилей распределения позволяет проводить анализ данных и оценивать вероятность появления определенных значений случайной величины. К примеру, определяя квантиль, можно сказать, в каком интервале находится большинство значений случайной величины или насколько большие значения она может принимать с заданной вероятностью.
Квантиль распределения: примеры использования
Примеры использования квантиля распределения:
- Построение доверительных интервалов: квантили распределения часто используются для определения значений, которые ограничивают интервалы, содержащие заданную вероятностную массу.
- Анализ риска: квантили распределения могут быть использованы для измерения и оценки риска в различных областях, таких как финансы, медицина и страхование.
- Статистический анализ данных: квантили распределения помогают определять критические значения для проверки гипотез и проведения статистических тестов.
- Прогнозирование: квантили распределения используются для определения доверительных интервалов для прогнозов и оценки вероятности определенных событий.
- Моделирование: квантили распределения могут быть использованы для оценки параметров моделей и создания новых моделей на основе данных.
В целом, квантили распределения играют важную роль в статистике и имеют множество применений в различных областях, где требуется анализ данных и вероятностной оценки.
Квантили распределения
Квантили распределения представляют собой измерения, используемые для определения значений во взятом наборе данных. Они представляют собой процентные значения, указывающие долю наблюдений, которые имеют значение менее или равное данному квантилю.
Квантили используются в различных областях, таких как статистика, экономика, финансы и многих других. Они позволяют оценить не только среднее значение, но и разброс данных и их распределение.
Квантили обозначаются числами от 0 до 1, представляющими процентную долю данных, находящихся ниже данного значения. Например, 0.25 квантиль показывает, что 25% наблюдений имеют значение меньше или равное данному квантилю, а 0.5 квантиль (или медиана) равна значению, разделяющему набор данных на две равные части.
Для расчета квантилей можно использовать различные методы, такие как эмпирические, перцентильные, интерполяционные, а также специфические для определенных распределений. На практике часто используются наиболее распространенные квантили: 0.25 (первый квартиль), 0.5 (медиана), 0.75 (третий квартиль).
Квантили распределения позволяют проводить анализ данных, определять выбросы, сравнивать различные группы данных и принимать решения на основе вероятностных оценок.
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 2, 3, 4} медианой, по определению, может служить любое число из интервала (2,3)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений.
Мода (статистика)
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
У этого термина существуют и другие значения, см. Мода (значения).
Мода — значение во множестве наблюдений, которое встречается наиболее часто. Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.
Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.
Абсолютное отклонение
В статистике абсолютное отклонение элементов в совокупности данных — абсолютная разница между элементом и выбранной точкой, от которой отсчитывается отклонение. В случаях, когда априорно известно, что выбранная точка является константой, а распределение элементов данных симметрично относительно неё, при отсутствии дополнительных данных, за точку отсчёта абсолютного отклонения принимается медиана или среднее значение рассматриваемой совокупности данных.
где
— абсолютное отклонение,
— элемент совокупности данных,
— одно из средних значений совокупности данных; это может быть среднее арифметическое (), но чаще всего в качестве среднего значения берется медиана.
Среднее абсолютное отклонение, или просто среднее отклонение (MAD – mean absolute deviation) — величина, используемая для оценки прогнозных функций:
Выбор среднего значения сильно влияет на среднее отклонение. Например, для совокупности {2, 2, 3, 4, 14}:
|
Среднее значение |
Среднее абсолютное отклонение |
|
Среднее арифметическое = 5 |
|
|
Медиана = 3 |
|
|
Мода = 2 |
Среднеквадратическое отклонение
Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.
Основные сведения
Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Среднеквадратическое отклонение:
стандартное отклонение (Оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещенной оценки ее дисперсии):
где — дисперсия; — i-й элемент выборки; — объём выборки; — среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещенными. В общем случае несмещенную оценку построить невозомжно. Однако оценка на основе оценки несмещенной дисперсии является состоятельной.
Приближенный метод проверки нормальности распределения
Квантиль распределения: определение и суть
Суть квантиля состоит в следующем: если мы имеем распределение данных, то квантиль позволяет вычислить значение, по которому данные делятся на две части, причем одна часть содержит заданную долю наблюдений. Как правило, доли выбираются в диапазоне от 0 до 1, что соответствует процентам от 0% до 100%, соответственно.
Например, 25-й квантиль (или первый квартиль) разделяет данные на две части таким образом, что 25% данных находятся слева от этого значения, а 75% данных – справа от него. Также существуют медиана (50-й квантиль) и 75-й квантиль (или третий квартиль), определяющие местоположение данных относительно их распределения.
Квантили широко используются в статистике и экономике для описания, изучения и обработки данных. Они помогают понять, как данные распределены и какой процент данных относится к определенной области. Квантили также полезны для строительства доверительных интервалов и анализа вероятностей в различных приложениях.
Пример
Теперь мы рассмотрели почти всю теоретическую часть, связанную с квантилем NumPy(). В этом разделе мы рассмотрим различные компоненты приложения на различных примерах. Мы начнем с примера элементарного уровня и постепенно будем продвигаться вверх.
#input import numpy as ppool a= print(ppool.quantile(a,.25)) print(ppool.quantile(a,.50)) print(ppool.quantile(a,.75))
Выход:
Выше мы можем увидеть простой пример квантиля. Здесь мы имеем дело с < сильным>четырехгрупповым квантилем, также называемым <сильным>квартилем. Сначала мы импортировали модуль NumPy. Затем они объявили 1-d массив. После чего мы использовали наш синтаксис и оператор print, чтобы получить желаемый результат. Как и любая другая статическая операция, во-первых, наши данные расположены в определенном порядке, обычно по возрастанию. После чего выполняется операция.
Теперь рассмотрим другой пример.
#input import numpy as ppool a=, ] print(ppool.quantile(a,.10)) print(ppool.quantile(a,.50)) print(ppool.quantile(a,1))
Выход:
В приведенном выше примере мы рассмотрели 2-мерный массив . Rest мы выполнили все шаги так же, как и в первом примере. Здесь мы имеем дело с < сильным>10 – групповым квантилем, который также известен как <сильные>децили. Здесь мы запросили выходные данные для (.1, .5 и 1) из программы, и наш вывод оправдывает это.
Далее давайте рассмотрим пример, который включает в себя некоторые из наших необязательных параметров.
#input import numpy as ppool a=, ] print(ppool.quantile(a,.50))))
Выход:
В приведенном выше примере мы рассмотрели аналогичный массив, как и в приведенном выше примере. Но в синтаксисе мы внесли определенные изменения, добавив необязательный параметр href=”https://en.wikipedia.org/wiki/Axis”>ось в первом случае без оси, где мы пытаемся найти квантиль со значением (.50). Здесь, поскольку мы не указали никакой оси, программа сплющила массив и обработала его как 1 одиночный массив вместо 2-d массива. В то время как во втором случае мы определили ось как 1, поэтому мы получаем значение квантиля отдельно для 2 суб-массивов. href=”https://en.wikipedia.org/wiki/Axis”>ось в первом случае без оси, где мы пытаемся найти квантиль со значением (.50). Здесь, поскольку мы не указали никакой оси, программа сплющила массив и обработала его как 1 одиночный массив вместо 2-d массива. В то время как во втором случае мы определили ось как 1, поэтому мы получаем значение квантиля отдельно для 2 суб-массивов.
Зачем нужно знать значение квантиля
1. Оценка рисков и принятие решений
Значение квантиля позволяет оценить вероятность наступления события и принять информированное решение на основе этой вероятности. Например, если вы знаете квантиль уровня 0.95 для доходности инвестиций, то вы можете оценить вероятность потери средств и принять решение о продолжении или прекращении инвестиций.
2. Измерение изменчивости
Значение квантиля можно использовать для измерения уровня изменчивости данных. Например, если вы знаете квантиль уровня 0.75 для продаж в определенный день, то это означает, что 75% продаж были ниже этого значения. Это позволяет оценить степень разброса в данных и принять соответствующие меры для управления рисками или оптимизации процессов.
3. Сравнение результатов
Значение квантиля позволяет сравнивать результаты различных наборов данных. Например, если вы сравниваете продажи в разные города, то зная значение квантиля уровня 0.9 для каждого города, вы сможете сказать, что 90% городов имеют продажи ниже этого значения. Это позволяет выявить лидеров и аутсайдеров, а также определить направления дальнейшего развития.
4. Моделирование и прогнозирование
Значение квантиля позволяет строить модели и прогнозировать будущие значения на основе статистической информации. Например, если вы знаете квантиль уровня 0.1 для цен на нефть, то можно прогнозировать, что с вероятностью 90% цена нефти будет выше этого значения. Это позволяет принимать решения о покупке или продаже активов на основе прогнозов и управлять рисками.
5. Определение целевых значений
Значение квантиля может быть использовано для определения целевых значений в бизнесе. Например, если вы знаете квантиль уровня 0.9 для прибыли от производства, то вы можете установить цель, чтобы 90% случаев приносили прибыль выше этого значения. Это поможет сориентировать команду на достижение заданных показателей и улучшение результатов.
Центральная тенденция: квантиль.
1)Квантильное понятие
Квантиль: упорядочивайте данные от малого к большему, разделите данные на n интервалов через n-1 квантиль, чтобы количество значений в каждом интервале было равным (приблизительно равным).
На примере квартилей данные делятся на 4 интервала по 3 квантиля. (Дециль имеет то же значение)
Первый квантиль становится квантилем 1/4 (нижний квартиль), а 1/4 данных в данных меньше этого квантиля.
Второй квантиль становится квантилем 2/4 (средний квартиль, также называемый медианой), а 2/4 данных меньше этого квантиля.
Третий квантиль становится 3/4 квантиля (нижний квартиль), а 3/4 данных в данных меньше этого квантиля.

2)Как найти квантиль
Учитывая набор данных (хранящихся в массиве), как рассчитать его значение квартиля? Первое, что необходимо прояснить, это то, что значение квартиля не обязательно совпадает с элементом массива.
В Python значение квартиля рассчитывается следующим образом:
① Сначала вычислите положение квартиля.
Среди них индекс позиции начинается с 1, а n — количество элементов в массиве.
② Рассчитайте значение квартиля в соответствии с положением.
Если index является целым числом (0 после десятичной точки), значение квартиля — это элемент, индексированный в массиве (обратите внимание, что индекс позиции начинается с 1). Если index не является целым числом, позиция квартиля находится между ceil (индекс) и floor (индекс), и значение квартиля определяется на основе элементов в этих двух позициях
Если index не является целым числом, позиция квартиля находится между ceil (индекс) и floor (индекс), и значение квартиля определяется на основе элементов в этих двух позициях.
3)Квантиль — это случай элементов в массиве
Результаты приведены ниже:

Нарисуйте графику:
Результаты приведены ниже:
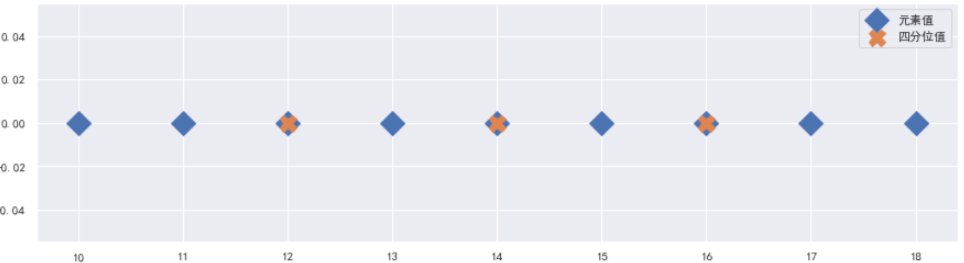
4)Квантиль не является элементом массива
Результаты приведены ниже:
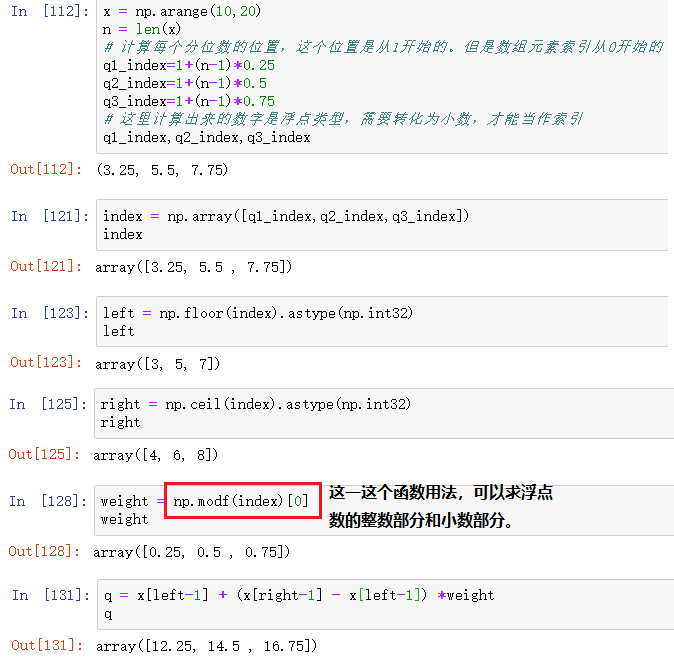
Нарисуйте графику:
Результаты приведены ниже:
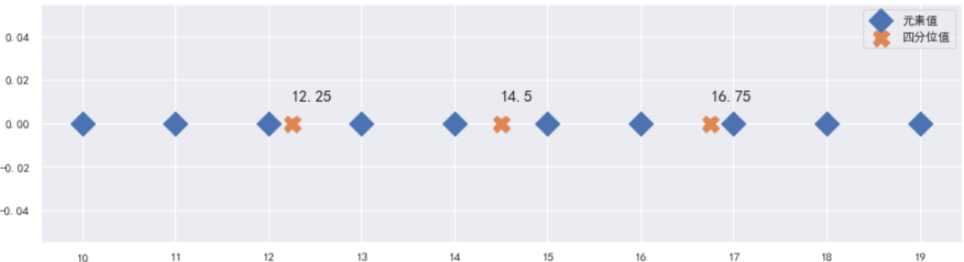
5)Функция для вычисления квантиля в numpy: quantile ()
Результаты приведены ниже:

Из результата видно, что приведенный выше результат квантиля, вычисленный нами, совпадает с результатом квантиля, вычисленным с использованием этой функции.
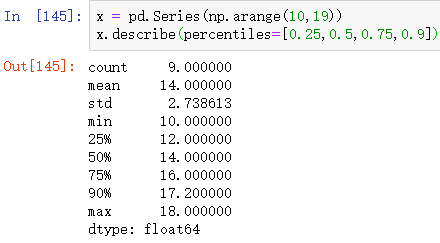
6)Функция для вычисления квантиля в пандах: description ()
Результаты приведены ниже:
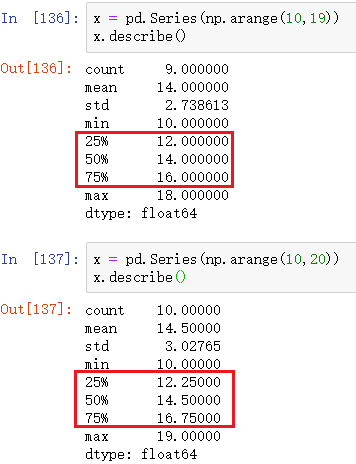
Примечание. Вы можете передать параметр процентилей в описании (), чтобы получить значение указанного квантиля.
Результаты приведены ниже:
Форма расчета квантилей
Квантили можно рассчитать с параметрической и непараметрической точки зрения. Давайте рассмотрим как более подробно, так и так называемую «квантильную функцию».
- Параметрический: Они используются в дистрибутивах, форма которых нам известна. То есть распределение будет нормальным, равномерным, экспоненциальным и так далее. Таким образом, предполагается, что он известен, а также его основные параметры (среднее арифметическое и дисперсия).
- Непараметрический: Он подходит для небольших образцов, где трудно узнать его точную форму, и поэтому мы не знаем его функцию распределения. Этот метод обеспечивает значения, аналогичные предыдущему при увеличении выборки, и, следовательно, использование обоих безразлично.
- Квантильная функция: Перед нами вероятностная форма расчета. Цель состоит в том, чтобы вычислить значение, которое имеет определенную вероятность в функции распределения. Мы не будем вдаваться в математические вопросы, усложняющие концепцию.
Наиболее частые квантили
Мы собираемся показать, какие квантили чаще всего используются в статистике. Большинство из них обычно используются для детального анализа распределения данных. Кроме того, еще одно его использование — разделение данных на группы с возможностью выбора самого высокого или самого низкого. В примере мы увидим это более подробно.
- Квартиль: Разделите значения на четыре равные группы и получите три квартиля. Это самый частый. Первый квартиль (Q1) — самые низкие данные, а третий квартиль (Q3) — самые высокие. С другой стороны, второй квартиль (Q2) соответствует медиане (Me), которая представляет собой статистику положения, которая делит распределение данных пополам. Значения квантилей будут 0,25 (Q1), 0,5 (Q2) и 0,75 (Q3).
- Квинтиль: Подобно предыдущему, он выполняется реже и делит данные на пять равных частей. Таким образом, есть четыре квинтиля. Значения квантилей в этом случае будут 0,20, 0,40, 0,60, 0,80.
- Дециль: В этом случае они разделены на десять частей и, следовательно, есть девять децилей. Опять же, это тоже не так уж часто. Их значения будут от 0,1 до 0,9.
- Процентили: Перед нами вариант, при котором раздача делится на сто равных частей. Это может быть интересно для очень больших выборок. Их значения варьируются от 0,01 до 0,99.
Общие языковые определения
В квантилях из в одномерном, дискретном (например , целое числе) или непрерывная (реальная) случайная величина являются значением , что переменное принимают для значений вероятности ниже квантиля считается, будучи стоит замечательного значения, например , 3 десятых, или 5 сотые и т. д. Их также называют -квантильными , полным синонимом в зависимости от контекста использования, и они являются взаимным значением функции распределения по вероятностному закону считается. Нас особенно интересуют некоторые наборы значений квантилей, соответствующие кратным простым долям 100% полной вероятности. Например, мы можем разделить 100% общую вероятность на 4 массы вероятностей, каждая из которых равна 1 ⁄ 4 = 25%, что соответствует для значений случайной величины четырем смежным интервалам. Таким образом, три промежуточных значения определяют, соответственно, фрактили 1 ⁄ 4 = 0,25, 1 ⁄ 2 = 0,5 и 3 ⁄ 4 = 0,75, или в единицах долей квантили четверти, половины и трех четвертей ( два крайних предела: нижний, соответствующий квантилю 0, и верхний, — квантилю 1, являются пределами области определения случайной величины.
В квантилях о наличии статистической выборки чисел замечательны значения позволяют разделить множество этих упорядоченные (т.е. отсортированные) данные в последовательные интервалы , содержащих одинаковое количество данных (к правильности целочисленного деления общего количества данных, кроме). Например, выборка из 90 данных может быть разделена на 10 последовательных подинтервалов с использованием набора из 9 квантилей (плюс нижний и верхний пределы области выборки).
Некоторым наборам квантилей даны определенные имена:
- квантили, кратные сотой, называются процентилями или процентилями в соответствии с частым англицизмом . Таким образом, 5- й процентиль разделяет выборку на 5% данных в ней, а остальные 95% — над ней. Последний процентиль ( 99- й ) часто играет чрезвычайно важную пороговую роль для мер, которые отражают интенсивность явления, подверженного критическим изменениям, и, таким образом, помогают в мониторинге (см. Ниже Пример определения 100-летнего наводнения в гидрологии );
- квантили, кратные одной десятой, являются децилями . Они часто используются в горной геологии (изучение гранулометрических характеристик разделенных материалов), гидрологии (определение уровней воды, включая паводки, 9- й дециль потока реки, устанавливающий ее уровень в год паводка ), а также в много медицинской статистики;
- квантили кратных квартала являются квартилями . Первый квартиль — это общая отмеченная статистика q 1 ; второй квартиль — не что иное, как медиана ; третий квартиль обозначается q 3, а интервал 1- го квартиля определяет межквартильный диапазон , который является традиционным измерением дисперсии выборки данных, однако более надежным, чем стандартное отклонение .
Все еще были определены четыре квинтиля и два терциля, которые используются редко.
Примечание : некоторые компьютерные программы определяют минимальный и максимальный квантиль соответственно квантилем 0 и квантилем 100%. Однако такая терминология выходит за рамки традиционных определений статистики.
Центральная тенденция
1)Среднее, медианное, понятие моды
Среднее: среднее значение, которое представляет собой сумму набора данных, деленную на количество данных.
Медиана: упорядочивайте группу данных в порядке возрастания, а значение в середине группы данных является медианной. Если количество данных четное, берется среднее из двух средних значений.
Режим: значение наиболее частого появления в наборе данных.
2)Разница между средним, медианным и модой
«Числовые переменные» обычно используют среднее и медиану для обозначения центральной тенденции.
«Категориальные переменные» обычно используют режим для обозначения центральной тенденции.
Поэтому при вычислении среднего оно подвержено экстремальным значениям. На расчет медианы и моды не влияют экстремальные значения, поэтому он будет относительно стабильным.
Режим не может быть уникальным в наборе данных. Но среднее и медиана уникальны.
При нормальном распределении все три одинаковы. При неравномерном распределении все три будут разными.
3)При разных распределениях соотношение между средним, медианой и модой
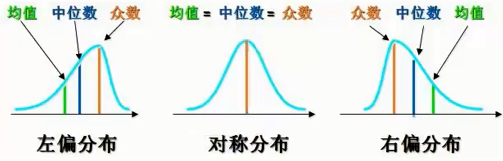
Метод запоминания: какая сторона хвоста длинная, называется «X частичным». Хвост слева длинный, он называется «косой влево», хвост справа длинный, называется «перекос вправо». Среднее значение находится ближе всего к хвосту, медиана всегда находится посередине, а мода — дальше всего от хвоста.
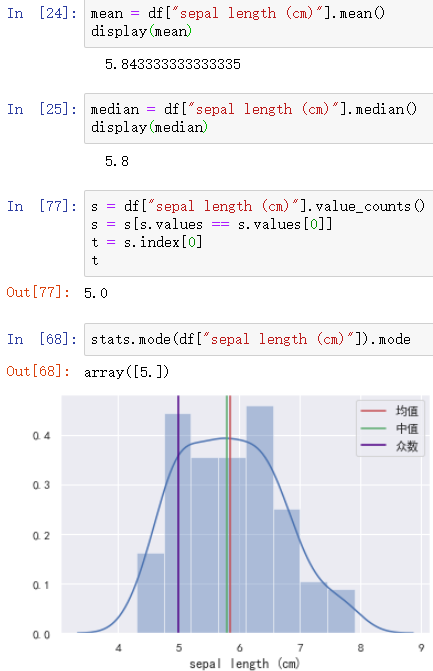
4)Код: вычислить среднее, медианное значение и моду длины чашечки в наборе данных радужки.
Результаты приведены ниже:
Квантиль в статистике
Квантиль – это показатель, который позволяет разделить упорядоченный набор данных на части определенной доли или вероятности. Квантили используются для анализа данных и распределений в статистике. Они помогают определить, какие значения находятся в заданном промежутке и как они распределены.
Квантили параметризуют распределение данных. Например, медиана – это 0,5-квантиль, так как она делит данные на две части такого же размера.
Существует несколько типов квантилей, но наиболее распространеными являются:
- Медиана (0,5-квантиль): делит данные на две равные половины.
- Первый квартиль (0,25-квантиль): разделяет данные так, что 25% значений находятся ниже него, а 75% – выше него.
- Третий квартиль (0,75-квантиль): разбивает данные так, что 75% значений находятся ниже него, а 25% – выше него.
Квантили широко применяются в статистике для изучения различных распределений, определения величин и вероятностей. Они могут использоваться для анализа экономических данных, оценки рисков, построения прогнозов и многое другое.
Например, при анализе финансовых данных квантили могут помочь определить, какая сумма денег будет достаточной для покрытия определенного процента риска. Также они могут использоваться для изучения распределения доходов населения и определения категорий населения с различным уровнем доходов.
В заключение можно сказать, что квантиль – это инструмент, который позволяет более глубоко проанализировать данные и получить показатели, имеющие практическую ценность в различных областях: экономике, социологии, медицине, физике и других науках.
Квантиль и регрессия
Квантили часто используются в статистике для анализа данных и построения моделей, таких как регрессия. Регрессия — это метод анализа данных, который позволяет определить зависимость между одной или несколькими независимыми переменными и зависимой переменной. Квантили играют важную роль в регрессионном анализе.
Когда мы строим регрессионную модель, мы пытаемся определить, как одна или несколько независимых переменных влияют на зависимую переменную. Мы можем использовать квантили, чтобы определить, какие значения независимых переменных связаны с определенными значениями зависимой переменной.
Например, представим себе модель, в которой мы пытаемся предсказать цену дома на основе таких факторов, как площадь дома, количество комнат и удаленность от центра города. Мы можем использовать квантили, чтобы определить, какие значения этих факторов связаны с определенными значениями цены дома.
Мы можем поделить наши данные на несколько квантилей, например, 25-й, 50-й и 75-й квантили, чтобы узнать, какие значения факторов связаны с ценой дома, находящейся в соответствующем квантиле. Например, если у нас есть данные о площади домов и ценах на эти дома, мы можем узнать, какие значения площади соответствуют низким ценам, а какие значения площади соответствуют высоким ценам, с помощью квантилей.
Зная эти связи, мы можем использовать квантили для предсказания цен на новые дома, исходя из их площади и других факторов. Квантили помогают определить диапазон возможных значений зависимой переменной, основываясь на независимых переменных.
Вывод: квантили играют важную роль в регрессионном анализе, позволяя нам определить связь между независимыми и зависимыми переменными и предсказывать значения зависимой переменной на основе значений независимых переменных.
Как найти квантиль вручную и с использованием статистического ПО
Квантиль — это значение данных, которое разделяет распределение на определенные доли. Найдя квантиль, можно понять, какое значение находится выше или ниже определенного порога. Ручной расчет квантилей может быть трудоемким и затруднительным при большом объеме данных. Однако, с помощью статистического ПО вычисление квантилей становится проще и быстрее.
Чтобы найти квантиль вручную, необходимо следующее:
- Отсортировать данные по возрастанию;
- Определить, на какую долю нужно поделить данные;
- Умножить долю на количество наблюдений (n);
- Найти целочисленную часть результата;
- Найти значение, соответствующее найденному номеру наблюдения.
Например, для нахождения медианы (50%-квантиля), необходимо разделить данные на две равные части. Если количество наблюдений четное, то медиана будет равна среднему арифметическому значений двух средних наблюдений. Если число наблюдений нечетное, то медиана определяется как значение серединного элемента.
Для нахождения квантиля с использованием статистического ПО, достаточно выбрать соответствующую команду и указать уровень значимости. Например, для R, команда quantile(dane, prob=c(0.25,0.5,0.75)) выведет значения 25%, 50% и 75%-квантилей для данных dane. Для Excel, можно использовать функцию QUARTILE, указав номер квантиля и диапазон данных.
Вывод: нахождение квантилей может быть сложным и трудоемким процессом. Однако, с использованием статистического ПО, расчет квантилей становится проще и быстрее
Тем не менее, стоит помнить о том, что интерпретация квантилей должна осуществляться с осторожностью, учитывая особенности распределения данных и выборку
Цикл for
Цикл обеспечивает перебор всех значений, поставляемых итератором. Он эквивалентен циклу в таких языках,
как C#.
Телом цикла может быть блок кода.
Как отмечено выше, цикл позволяет проходить по всем элементам объекта, имеющего итератор, например:
- обладающего внутренней или внешней функцией , возвращаемый тип которой :
- обладает внутренней или внешней функцией
- обладает внутренней или внешней функцией , возвращающей .
Все три указанные функции должны быть объявлены как .
Чтобы перебрать диапазон чисел, используйте выражение диапазона:
Цикл по диапазону или массиву компилируется в основанный на индексе цикл, который не создает объект итератора.
Если при проходе по массиву или списку необходим порядковый номер элемента, используйте следующий подход:
Также вы можете использовать библиотечную функцию .






























