Страница 31 — гдз математика 4 класс. моро, бантова. учебник часть 1

Что такое центральная симметрия

Точки А и А1 называются симметричными относительно точки О, если О — середина АА1.

Рисунок 1. Центральная симметрия в снежинке. 

Например, центр симметрии:

• окружности — центр окружности;
• параллелограмма — точка пересечения его диагоналей;
• прямой — любая точка прямой, то есть бесконечное множество центров симметрии.

Фигуру можно называть симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. 

Фигуры, симметричные относительно некоторой точки, равны. 

Одним из первых ученых, подробно изучавшим центральную симметрию, был выдающийся немецкий математик Феликс Клейн. При изучении геометрии, утверждал Клейн, нужно рассматривать не только объекты (треугольники, окружности и т.д.), но и перемещения.

В классической геометрии Евклида более двух тысяч лет под перемещениями понимались только движения твердого тела: можно взять фигуру и поместить ее копию в новое место. При подходе Клейна геометрия охватывает гораздо более широкий класс задач, чем в классическом понимании. 

1. Доказательство с помощью векторов: Пусть точки A и B отобразились соответственно на A1 и B1, а О — центр симметрии. Тогда, из определения центральной симметрии, векторы OA1 = -OA, OB1 = -OB.

Рассмотрим вектор A1B1 = OB1 — OA1= -(OB)-(-OA)= -OB+OA= -(OB-OA)= -AB.

Следовательно, центральная симметрия является движением, изменяющим направление на противоположное.

2. Доказательство геометрическим методом. 

Дано: точки А и В, точка О — центр, А1, В1 — образы исходных точек, АО=ОА1, ВО=ОВ1. 

Доказать, что АВ=А1В1. 

Рисунок 2. 

Решение: 

Рассмотрим ΔAOB и ΔA1OB1 (рисунок 2). По условию: 

1. AO=A1O.
2. BO=B1O.
3. 3. ∠AOB=∠A1OB1, так как это вертикальные углы.

1,2,3 ⇒ ΔAOB = ΔA1OB ⇒ AB=A1B1. Что и требовалось доказать. 

Фигуры, обладающие симметрией

Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Пример №1

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

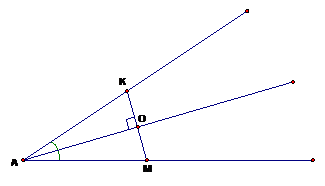
Рассмотрим Δ KAO и Δ MAO:

• AO – общая сторона
• Из свойства биссектрисы: ∠ MAO = ∠KAO
• Треугольники KAO и MAO прямоугольные,

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

Пример №2

Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

Пример №3

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Пример №4

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Пример №5

Пример №6

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Применение

В математике

Единичный квадрат используется как эталон единицы измерения площади, а также в определении площади произвольных плоских фигур. Фигуры, у которых можно определить площадь, называются квадрируемыми.

Теорема Пифагора первоначально формулировалась геометрически: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Квадратами являются грани куба — одного из пяти правильных многогранников.

В математической физике символ квадрата может означать «оператор Д’Аламбера» (даламбериан) — дифференциальный оператор второго порядка:

u:=∂2u∂x2+∂2u∂y2+∂2u∂z2−1c2∂2u∂t2{\displaystyle \square u:={\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}}

Из теоремы Бойяи — Гервина следует, что любой многоугольник равносоставлен квадрату, то есть его можно разрезать на конечное число частей, из которых составляется квадрат (и обратно).

Графы:
K₄полный граф часто изображается как квадрат с шестью рёбрами.

3-симплекс (3D)

Другие применения

Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.

Квадратный флаг Лима поделён на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.

Графика

Ряд символов имеют форму квадрата:

• Символы Юникода U+25A0 — U+25CF
• U+20DE ◌⃞ COMBINING ENCLOSING SQUARE
• ロ (Японский иероглиф «Ро» (катакана))
• 口 (Китайский иероглиф «рот»)
• 囗 (Китайский иероглиф «ограда»)

В Latex для вставки символа квадрата служат конструкции или .

В HTML, чтобы заключить произвольный текст в квадрат или прямоугольник, можно использовать конструкцию:

text; результат: text.

Примеры фигур, обладающих центральной симметрией

Рисунок 2. Примеры геометрических фигур с центром симметрии.

В повседневной жизни нас также окружают предметы, обладающие центральной симметрией. Она видна в строении кристаллов и снежинок, которые являются кристаллами льда. Их формы сложные и многообразные, но все они центрально симметричны. В природе это также цветы (подсолнух, ромашка, астра) и некоторые растения, а в искусстве — необычные орнаменты и строения архитектуры. 

Рисунок 3. Примеры центральной симметрии в окружающем мире. 

Не обладают центральной симметрией: угол, произвольный треугольник, трапеция, неправильные многоугольники. 

Имеют и осевую, и центральную симметрию: квадрат, окружность, ромб и др.  

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы. 

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Теорема и доказательство

Теорема

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется. 

Если отрезок MN симметричен отрезку M₁N₁  относительно прямой a, то MN = M₁N₁. 

Чтобы доказать, что MN = M₁N₁, сделаем дополнительные построения:

• P – это точка пересечения MM₁ и прямой a;
• Q – это точка пересечения NN₁ и прямой a; 
• построим отрезок MK, перпендикулярный NN₁;
• тогда точка K отразится в точку K₁.

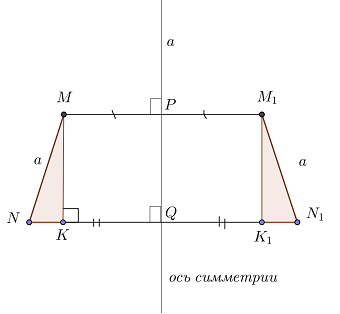
Докажем, что прямоугольные треугольники MNK и M₁N₁K₁ равны. Стороны MN и M₁N₁ являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

МК = М₁К₁ , так как перпендикулярны к параллельным прямым.

По построению:

NK = NQ – KQ,

N₁K₁ = N₁Q – K₁Q. 

Точка N отобразилась в точку N₁,  значит:

NK = N₁K₁.

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть  MN = M₁N₁, что и требовалось доказать.

Основные понятия симметрии и ее виды.

Понятие симметрии пр
оходит
через всю историю человечества. Оно
встречается уже у истоков человеческого
знания. Возникло оно в связи с изучением
живого ор­ганизма, а именно человека.
И употреблялось скульпторами ещё в 5
веке до н. э. Слово “симметрия” греческое,
оно означает “соразмерность,
пропорциональность, одинаковость в
расположении частей”. Его широко
используют все без исключения направления
современной науки. Об этой закономерности
задумывались многие ве­ликие люди.
Например, Л. Н. Толстой говорил: “Стоя
перед черной доской и рисуя на ней мелом
разные фигуры, я вдруг был поражен
мыслью: почему симметрия по­нятна
глазу? Что такое симметрия? Это врожденное
чувство, отвечал я сам себе. На чем же
оно основано?”. Действительно
симметричность приятна глазу. Кто не
любо­вался симметричностью творений
природы: листьями, цветами, птицами,
живот­ными; или творениями человека:
зданиями, техникой, – всем тем, что нас
с детства окружает, тем, что стремится
к красоте и гармонии. Герман Вейль
сказал: “Симмет­рия является той
идеей, посредством которой человек на
протяжении веков пытался постичь и
создать порядок, красоту и совершенство”.
Герман Вейль – это немецкий математик.
Его деятельность приходится на первую
половину ХХ века. Именно он сформулировал
определение симметрии, установил по
каким признакам усмотреть наличие или,
наоборот, отсутствие симметрии в том
или ином случае. Таким обра­зом,
математически строгое представление
сформировалось сравнительно недавно
– в начале ХХ века. Оно достаточно
сложное. Мы же обратимся и еще раз
вспомним те определения, которые даны
нам в учебнике.

Свойства

Далее в этом разделе a{\displaystyle a} обозначает длину стороны квадрата, d{\displaystyle d} — длину диагонали, R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности.

Стороны и диагонали

Диагонали квадрата равны, взаимно перпендикулярны, делятся точкой пересечения пополам и сами делят углы квадрата пополам (другими словами, являются биссектрисами внутренних углов квадрата). Длина каждой диагонали d=a2.{\displaystyle d=a{\sqrt {2}}.}

Периметр квадрата P{\displaystyle P} равен:

P=4a=42R=8r{\displaystyle P=4a=4{\sqrt {2}}R=8r}.

Вписанная и описанная окружности

Вписанная и описанная окружности для квадрата

Центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей.

Радиус вписанной окружности квадрата равен половине стороны квадрата:

r=a2.{\displaystyle r={\frac {a}{2}}.}

Радиус описанной окружности квадрата равен половине диагонали квадрата:

R=22a.{\displaystyle R={\frac {\sqrt {2}}{2}}a.}

Из этих формул следует, что площадь описанной окружности вдвое больше площади вписанной.

Площадь

Площадь S{\displaystyle S} квадрата равна

S=a2=2R2=4r2=12d2{\displaystyle S=a^{2}=2R^{2}=4r^{2}={1 \over 2}d^{2}}.

Из формулы S=a2,{\displaystyle S=a^{2},} связывающей сторону квадрата с его площадью, видно, почему возведение числа во вторую степень традиционно называется «возведением в квадрат», а результаты такого возведения называются «квадратными числами» или просто квадратами. Аналогично корень 2-й степени называется квадратным корнем.

Квадрат имеет два замечательных свойства.

1. Из всех четырёхугольников с заданным периметром квадрат имеет наибольшую площадь.
2. Из всех четырёхугольников с заданной площадью квадрат имеет наименьший периметр.

К уравнению квадрата; здесь R=2,x=y={\displaystyle R=2,x_{0}=y_{0}=0}

Уравнение квадрата

В прямоугольной системе координат уравнение квадрата с центром в точке {x,y}{\displaystyle \{x_{0},y_{0}\}} и диагоналями, параллельными осям координат (см. рисунок), может быть записано в виде:

|x−x|+|y−y|=R,{\displaystyle |x-x_{0}|+|y-y_{0}|=R,}

где R{\displaystyle R} — радиус описанной окружности, равный половине длины диагонали квадрата. Сторона квадрата тогда равна R2,{\displaystyle R{\sqrt {2}},} его диагональ равна 2R,{\displaystyle 2R,} а площадь квадрата равна 2R2.{\displaystyle 2R^{2}.}

К уравнению квадрата

1. |x−y|+|x+y|=a{\displaystyle |x-y|+|x+y|=a} (легко получается применением поворота на 45° к предыдущему уравнению)
2. max(x2,y2)=r2{\displaystyle \max(x^{2},y^{2})=r^{2}}
3. (в полярных координатах) r(φ)=min(r|cos⁡φ|,r|sin⁡φ|){\displaystyle \quad r(\varphi )=\min \left({\frac {r}{|\cos \varphi |}},{\frac {r}{|\sin \varphi |}}\right)}

Математические проблемы

Пример квадрирования квадрата 112×112{\displaystyle 112\times 112}

С квадратами связаны ряд проблем, часть из которых до сих пор не имеет решения.

• Квадратура круга — древняя проблема построения циркулем и линейкой квадрата, равновеликого по площади заданному кругу. В 1882 году Фердинанд Линдеман доказал, что это невозможно.
• Квадрирование квадрата — задача о разбиении квадрата на конечное число меньших квадратов, без «дырок», причём длины сторон квадратов должны отличаться друг от друга (в идеале должны быть все различны). Найден ряд решений этой задачи.
• Долгое время математики пытались доказать, что непрерывное отображение отрезка прямой в квадрат невозможно, пока Джузеппе Пеано не построил свой контрпример.
• Гипотеза Тёплица: на всякой замкнутой плоской жордановой кривой можно отыскать четыре точки, образующие вершины квадрата. Не доказана и не опровергнута.
• Разбиение квадрата сеткой одинаковых более мелких квадратов также приводит к множеству проблем, используемых, в частности, в теории латинских и греко-латинских квадратов, магических квадратов, в игре судоку.

Симметрия

Линии симметрии

Квадрат обладает наибольшей осевой симметрией среди всех четырёхугольников. Он имеет:

• одну ось симметрии четвёртого порядка — ось, перпендикулярную плоскости квадрата и проходящую через его центр;
• четыре оси симметрии второго порядка (то есть относительно них квадрат отражается сам в себя), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.

Центральная симметрия

3.1
Основные определения

Определение
.

Две точки А и А 1
называются симметричными относительно
точки О, если О — середина отрезка АА 1 .
Точка О считается симметричной са­мой
себе.

Определение.

Фигура
называется симметричной относительно
точки О, если для каждой точки фигуры
симметричная ей точка относительно
точки О также принадлежит этой фигуре.

3.2
План построения

Построение
треугольника симметричного данному
относительно цен­тра О.

Чтобы построить
точку, симметричную точке А
относи­тельно
точки О
,
достаточно провести прямую ОА
(рис. 46)
и по другую
сторону от точки О
от­ложить
отрезок, равный отрезку ОА
.
Иными
словами,

точки А
и
;
В и
;
С и

симметричны
относительно некоторой точки
О. На рис. 46
по­строен треугольник, симметричный
треуголь­нику ABC
относительно
точки О.
Эти
треугольники равны.

Построение симметричных точек
относительно центра.

На рисунке точки М
и М 1 ,
N и N 1
симметричны относительно точки О, а
точки Р и Q не симметричны относительно
этой точки.

Вообще фигуры,
симметричные относительно некоторой
точки, равны.

3.3
Примеры

Приведём примеры
фигур, обладающие центральной симметрией.
Простейшими фигурами, обладающими
центральной симметрией, является
окружность
и паралле­лограмм.

Точка О называется
центром симметрии фигуры. В подобных
случаях фигура обладает центральной
симметрией. Центром
симметрии окружности является центр
окружности, а центром симметрии
параллелограмма- точка пересечения его
диаго­налей.

Прямая также обладает
центральной симметрией, однако в отличие
от окруж­ности и параллелограмма,
которые имеют только один центр симметрии
(точка О на рисунке) у прямой их бесконечно
много — любая точка прямой является её
центром симметрии.

На рисунках показан
угол симметричный относительно вершины,
отрезок сим­метричный другому отрезку
относительно центра А

и четырехугольник симметрич­ный
относительно своей вершины М.

Примером фигуры, не имеющей центра
симметрии, является треугольник.