Десятичная система счисления. классы и разряды

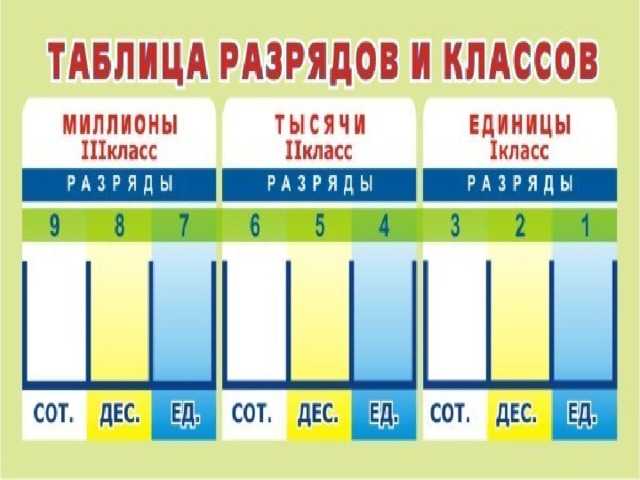
Разрядность чисел

Разряд
— это место (позиция), на котором в записи числа стоит цифра.

Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.

Разряды отсчитываются с конца числа.

Разряд единиц
— это самый младший разряд, которым заканчивается любое число.

Цифра «5» — означает «5» единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).

Разряд десятков
— это разряд, который стоит перед разрядом единиц.

Цифра «5» — означает «5» десятков, если она стоит на предпоследнем месте (в разряде десятков).

Разряд сотен
— это разряд, который стоит перед разрядом десятков. Цифра «5» означает «5» сотен, если она стоит на третьем месте от конца числа (в разряде сотен).

Пример. В числе «807» содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа
.807 = 8 сотен 0 десятков 7 единиц

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.

Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.

Сумма разрядных слагаемых

Любое натуральное число можно записать в виде суммы разрядных слагаемых.

Как это делается, видно из следующего примера: число 999 состоит из 9 сотен, 9 десятков и 9 единиц, поэтому:

999 = 9 сотен + 9 десятков + 9 единиц = 900 + 90 + 9

Числа 900, 90 и 9 – разрядные слагаемые. Разрядное слагаемое
– это просто количество единиц в данном разряде.

Сумму разрядных слагаемых также можно записать следующим образом:

999 = 9 · 100 + 9 · 10 + 9 · 1

Числа, на которые выполняется умножение (1, 10, 100, 1000 и т. д.), называются разрядными единицами
. Так, 1 – это единица разряда единиц, 10 – единица разряда десятков, 100 – единица разряда сотен и т. д. Числа, которые умножаются на разрядные единицы выражают количество разрядных единиц
.

Запись любого числа в виде:

12 = 1 · 10 + 2 · 1 или 12 = 10 + 2

называется разложением числа на разрядные слагаемые
(или суммой разрядных слагаемых
).

3278 = 3 · 1000 + 2 · 100 + 7 · 10 + 8 · 1 = 3000 + 200 + 70 + 8 5031 = 5 · 1000 + 0 · 100 + 3 · 10 + 1 · 1 = 5000 + 30 + 1 3700 = 3 · 1000 + 7 · 100 + 0 · 10 + 0 · 1 = 3000 + 700

Задание № 4

Запиши пять чисел (рис. 4), каждое из которых содержит 37 десятков. Сколько таких чисел можно записать?

Решение: 1 37 десятков – это число 370. Если менять количество единиц, то количество десятков не изменится, поэтому запишем 370, 371, 372, 373, 374.

2. Всего таких чисел можно записать десять: 370, 371, 372, 373, 374, 375, 376, 378, 379.

Список литературы

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
2. Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
3. Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / – 2-е изд. – М.: Просвещение, 2012., ст. 51 № 1–5.
2. Назови правило, по которому можно определить общее число единиц или десятков, или сотен в числе.
3. Сколько можно написать трёхзначных чисел, у которых 52 десятка?
4. * Сколько единиц составляет семь сотен? А сколько единиц в 70 десятках? Сравни полученные числа.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

“>

Правило встречается в следующих упражнениях:

2 класс

Страница 41. Урок 21,
Петерсон, Учебник, часть 1

Страница 42. Урок 22,
Петерсон, Учебник, часть 1

Страница 43. Урок 22,
Петерсон, Учебник, часть 1

Страница 48. Урок 25,
Петерсон, Учебник, часть 1

Страница 65. Урок 33,
Петерсон, Учебник, часть 1

Страница 35. Урок 12,
Петерсон, Учебник, часть 3

3 класс

Страница 82. Урок 30,
Петерсон, Учебник, часть 1

Страница 85. Урок 31,
Петерсон, Учебник, часть 1

Страница 89. Урок 33,
Петерсон, Учебник, часть 1

Страница 15. Урок 6,
Петерсон, Учебник, часть 2

Страница 48. Урок 19,
Петерсон, Учебник, часть 2

Страница 92. Урок 40,
Петерсон, Учебник, часть 2

Страница 95. Урок 42,
Петерсон, Учебник, часть 2

Страница 37. Урок 17,
Петерсон, Учебник, часть 3

Страница 54. Урок 24,
Петерсон, Учебник, часть 3

Страница 67. Повторение,
Петерсон, Учебник, часть 3

4 класс

Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 24,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 76. Тест. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 77. Тест. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 114,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 27,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 33. Урок 11,
Петерсон, Учебник, часть 1

5 класс

Номер 846,
Мерзляк, Полонский, Якир, Учебник

Номер 847,
Мерзляк, Полонский, Якир, Учебник

Номер 851,
Мерзляк, Полонский, Якир, Учебник

Номер 852,
Мерзляк, Полонский, Якир, Учебник

Номер 853,
Мерзляк, Полонский, Якир, Учебник

Номер 854,
Мерзляк, Полонский, Якир, Учебник

Номер 856,
Мерзляк, Полонский, Якир, Учебник

Номер 858,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Классы и разряды

В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.

Класс единиц
или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен
.

Пример.

Числа	Класс единиц (первый класс)
сотни	десятки	единицы
6	—	—	6
34	—	3	4
148	1	4	8

Класс тысяч
или второй класс — это класс, который образуют следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч.

Пример.

Числа	Класс тысяч (второй класс)	Класс единиц (первый класс)
сотни тысяч	десятки тысяч	единицы тысяч	сотни	десятки	единицы
5234	—	—	5	2	3	4
12 803	—	1	2	8	3
356 149	3	5	6	1	4	9

Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу (единицу следующего разряда: единицу тысяч в классе тысяч).

10 сотен = 1 тысяча

Класс миллионов
или третий класс — это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.

Единица разряда миллионов — это один миллион или тысяча тысяч (1 000 тысяч). Один миллион можно записать в виде числа 1 000 000.

Десять таких единиц образуют новую разрядную единицу — десять миллионов (10 000 000).

Десять десятков миллионов образуют новую разрядную единицу — сто миллионов или в записи цифрами 100 000 000.

Пример.

Числа	Класс миллионов (третий класс)	Класс тысяч (второй класс)	Класс единиц (первый класс)
сотни миллионов	десятки миллионов	единицы миллионов	сотни тысяч	десятки тысяч	единицы тысяч	сотни	десятки	единицы
8 345 216	—	—	8	3	4	5	2	1	6
93 785 342	—	9	3	7	8	5	3	4	2
134 590 720	1	3	4	5	9	7	2

Задание 2

За­пи­ши­те циф­ра­ми числа:

1. Сто во­семь тысяч три­ста де­вять

2. Трид­цать тысяч семь­сот де­вять

3. Во­семь тысяч шесть­сот

Ре­ше­ние

Мно­го­знач­ные числа за­пи­сы­ва­ют по клас­сам, на­чи­ная с выс­ше­го. Чтобы за­пи­сать циф­ра­ми число, на­при­мер «сто во­семь тысяч три­ста де­вять», сна­ча­ла за­пи­сы­ва­ют, сколь­ко всего еди­ниц вто­ро­го, выс­ше­го, клас­са в числе – 108, потом за­пи­сы­ва­ют, сколь­ко всего еди­ниц пер­во­го клас­са в числе.

Для числа «трид­цать тысяч семь­сот семь­де­сят» за­пи­шем ко­ли­че­ство еди­ниц вто­ро­го выс­ше­го клас­са в числе, их трид­цать, и ко­ли­че­ство еди­ниц пер­во­го клас­са в числе, семь­сот семь­де­сят.

В числе «во­семь тысяч шесть­сот» 8 еди­ниц вто­ро­го клас­са и шесть­сот еди­ниц пер­во­го клас­са.

2 класс – класс тысяч	1 класс – класс еди­ниц
Сотни  тысяч	Де­сят­ки тысяч	Еди­ни­цы тысяч	Сотни	Де­сят­ки	Еди­ни­цы
1	8	3	9
	3	7	7
		8	6

Что такое натуральное число

Слово «натуральный» обозначает природный, естественный. То есть, натуральное число — это число, которое получается естественным образом при подсчёте чего-либо. 

Ноль не является натуральным числом, ведь ноль — это пустота, нисколько предметов. 

Отрицательные числа, перед которыми стоит знак минуса, такие как -1, -19, -327, не являются натуральными, потому что они обозначают то, чего не хватает. Следовательно, их нельзя посчитать. 

Нецелые числа, те, которые обозначают половину, треть, четверть и тому подобное, тоже не относятся к натуральным.

Самое маленькое натуральное число — 1. 

Натуральных чисел бесконечно много, потому что, если представить себе самое-самое большое натуральное число, то всё равно к нему можно прибавить 1, и получится ещё большее число. Бесконечность натуральных чисел обозначается латинской буквой N. 

Практика:

Попросите ребёнка посмотреть вокруг себя и сосчитать, сколько он видит книг, сколько тетрадок и сколько ручек.

Например, 8 книг, 2 тетради и 1 ручка.

8, 2 и 1 — это натуральные числа. Они обозначаются такими же цифрами: 8, 2 и 1.

Образуем числа

Ниже приведены примеры упражнений, направленных на отработку понимания образования чисел. Их необходимое количество будет зависеть от уровня развития учеников класса.

1. Используя рисунок, расскажите, как образовалось число. Прочитайте его (2 сотни, 4 десятка, 3 единицы). Число изображено геометрическими фигурами, например, большими и маленькими треугольниками, точками.
2. Запишите и прочитайте числа. Изобразите их при помощи геометрических фигур. (Учитель читает: «2 сотни, 8 десятков, 6 единиц». Дети слушают задание, затем последовательно выполняют его).
3. Продолжите запись по образцу. Прочитайте числа и изобразите их с помощью модели. (4 сот. 8 ед. = 4 сот. 0 дес. 8 ед. = 408; 3 сот. 4 ед. = … сот. … дес. … ед. = …).

Классы и разряды

В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.

Класс единиц
или первый класс — это класс,
который образуют первые три разряда
(справа от конца числа): разряд единиц, разряд десятков и разряд сотен
.

Класс тысяч
или второй класс — это класс, который образуют следующие
три разряда: единицы тысяч, десятки тысяч и сотни тысяч.

сотни тысяч

десятки тысяч

единицы тысяч

сотни

десятки

единицы

Напоминаем, что 10
единиц разряда сотен (из класса единиц) образуют одну тысячу
(единицу следующего разряда: единицу тысяч в классе тысяч).

Класс миллионов
или третий класс — это класс, который
образуют следующие три разряда:
единицы миллионов, десятки миллионов и сотни миллионов.

Единица разряда миллионов — это один миллион или тысяча тысяч (1 000
тысяч).
Один миллион можно записать в виде числа «1 000 000
».

Десять таких единиц образуют новую разрядную единицу —
десять миллионов « 10 000 000
»

Десять десятков миллионов образуют
новую разрядную единицу — сто миллионов или в записи цифрами
«100 000 000
».

сотни миллионов

десятки миллионов

единицы миллионов

сотни тысяч

десятки тысяч

единицы тысяч

сотни

десятки

единицы

сотни миллионов

десятки миллионов

единицы миллионов

сотни тысяч

десятки тысяч

единицы тысяч

сотни

десятки

единицы

Как прочитать многозначное число

Запомните!

Не произносят название класса единиц, а также название класса, все три цифры которого нули.

Например, число «134 590 720
» читаем:
сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот
двадцать.

Число «418 000 547
» читаем: четыреста восемнадцать миллионов пятьсот сорок семь.

На нашем сайте
для проверки своих результатов
вы можете
воспользоваться калькулятором разложения числа на разряды онлайн .

Важно!

Десятичная система счисления

Когда древние люди научились считать, им понадобилось как-то обозначать количество. Сначала для этого использовались собственные пальцы, но это было не очень-то удобно, потому что пальцев на руках и ногах всего двадцать, а предметов может быть больше. 

Тогда люди придумали специальные символы, которые назвали цифрами. Цифры бывают арабскими и римскими. 

Арабские цифры выглядят вот так:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Римские цифры выглядят вот так:

I, II, III, IV, V, VI, VII, VIII, IX, X

Римскими цифрами не очень удобно пользоваться, поэтому в математике мы используем арабские. Их всего десять, поэтому арифметические действия, производимые с их помощью, называются десятичной системой счисления.

Свойства натуральных чисел

Сложение, вычитание, умножение и деление подчиняются законам арифметики. Всего этих законов, основанных на свойствах натуральных чисел, пять.

1. Переместительный закон сложения.

При сложении можно менять порядок слагаемых чисел как угодно — результат всегда будет одинаковым.

5 + 7 = 12 и 7 + 5 = 12

24 + 6 + 8 = 38 и 6 + 24 + 8 = 38 и 8 + 6 + 24 = 38

2. Переместительный закон умножения.

При умножении можно менять порядок множителей как угодно — результат всегда будет одинаковым.

2 х 4 = 8 и 4 х 2 = 8

4 х 3 х 5 = 60 и 3 х 5 х 4 = 60 и 5 х 4 х 3 = 60

3. Сочетательный закон сложения.

При сложении трёх чисел можно сложить первое и второе, и к их сумме прибавить третье, а можно сложить второе и третье, и к их сумме прибавить первое — результат будет один и тот же.

(5 + 7) + 8 = 12 + 8 = 20 и 5 + (7 + = 5 + 15 = 20

17 + (4 + 23) = 17 + 27 = 44 и (17 + 23) + 4 = 40 + 4 = 44

4. Сочетательный закон умножения.

Когда умножаем три числа, то результат не изменится, если перемножать множители не по порядку.

3 х (2 х 5) = 30 и (3 х 5) х 2 = 30

5. Распределительный закон.

Результат умножения суммы на число будет равен результату сложения произведений каждого слагаемого суммы на это число.

5 х (3 + 4) = 5 х 3 + 5 х 4 = 35

Вот мы и познакомились с основной информацией о натуральных числах. Мы используем их каждый день: считаем, сколько ложечек сахара положить в чай, сколько бензина залить в машину. С помощью натуральных чисел мы определяем, что выгодней: купить три маленьких коробочки с печеньем или одну большую. Вычисляем, на сколько долек разрезать яблоко, чтобы угостить сестру, маму, папу — и полакомиться самому. Поэтому обязательно учитесь пользоваться натуральными числами — и они обязательно ещё не раз сослужат вам добрую службу.

Знания лучше всего закрепляются в памяти, если ребёнок применяет их на практике, выполняя интересные задания. Такую возможность предоставляет образовательная платформа iSmart. Здесь представлены онлайн-тренажёры, разработанные в соответствии с образовательными стандартами РФ, являющиеся эффективным вспомогательным инструментом для усвоения школьной программы.

Есть разделы по математике, русскому и английскому языкам, окружающему миру, логике и другим предметам. Кроме упражнений для закрепления материала есть также возможность подготовиться к ВПР и контрольным работам. 

Зарегистрируйте своего ребёнка на образовательной платформе iSmart, чтобы начать занятия.

Примеры решения задач

Для чего требуется знание числовых разрядов на практике? Для правильного нахождения суммы и разности чисел. 

Хотя подобные примеры можно решить онлайн, полезнее уметь просчитывать их самостоятельно. Вычисления проводятся при помощи сложения или вычитания в столбик или

Задача 1

Найти сумму 135 и 241.

Для этого требуется сложить 135 и 241. При этом единицы складываются с единицами и так далее. Поэтому сначала нужно охарактеризовать позицию цифр каждого из слагаемых.

Далее производится сложение — 135 + 241:

• друг к другу прибавляются единицы – 1 + 5 = 6;

• складываются десятки – 3 + 4 = 7;

• складываются сотни – 1 + 2 = 3.

+	1	3	5
2	4	1
	3	7	6

Сходным образом выполняется вычитание.

Задача 2

Найти разность 567 и 254:

• сначала вычитаются значения единиц 7 – 4 = 3;

• отнимают десятки 6 – 5 = 1;

• вычитают сотни 5 – 2 = 3.

—	5	6	7
2	5	4
	3	1	3

Ответ: 313.

Если постоянно упражняться в решении примеров, начиная с самых простых, которые изучаются в 1 классе, и постепенно усложняя, многие арифметические действия можно вычислять устно, тренируя тем самым свой ум, внимание, память и сообразительность.

Разряды натурального числа. Значение разряда

Место, которое цифра занимает в числе, называется разрядом. От этого места зависит её значение. Всего есть три разряда: единицы, десятки и сотни.

Разряды могут быть старшими и младшими. Старшими считаются разряды, которые располагаются слева, а младшими — справа. Самый младший — это всегда разряд единиц. 

В числе 42 цифра 4 обозначает четыре десятка, это старший разряд. Цифра 2 обозначает две единицы, это младший разряд.

В числе 4762 самый старший разряд — тысячный, он обозначен цифрой 4. Цифра 7 — это разряд сотен, он младше разряда тысяч, но старше разряда десятков. Цифра 6 младше и разряда тысяч, и разряда сотен, но старше разряда единиц. 2 — самый младший разряд.  

Количество разрядов всегда такое же, как и количество цифр в числе.

42 — две цифры, два разряда: разряд десятков и разряд единиц.

891 — три цифры, три разряда: разряд сотен, разряд десятков, разряд единиц.

Практика:

Предложите ребёнку самостоятельно определить разряды в следующих числах:

607, 23, 1126.

Числа и цифры

Числа являются единицами исчисления. Используя числа, вы можете подсчитать количество объектов и определить различные значения.

Для записи цифр используются специальные символы — цифры. Их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

• Один (1) — это наименьшее число, и это не самое большое число.
• Ноль (0) означает отсутствие элемента. Ноль не является натуральным числом.

Имя зависит от количества цифр в числе.

Число, имеющее только одну цифру, называется однозначным. Самая маленькая однозначная цифра — 1, самая большая — 9.

Число, состоящее из двух цифр, называется двузначным числом. Самое маленькое двузначное число — 10, самое большое — 99.

Числа, записанные двумя, тремя, четырьмя и более цифрами, называются двузначными, трехзначными, четырехзначными или многозначными. Самое маленькое трехзначное число — 100, самое большое — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Классы и разряды

классы

Для того чтобы прочесть число, его разбивают справа налево на группы по три цифры в каждой. Эти группы называются классами.

• Первый класс справа называют классом единиц, 
• второй — классом тысяч,
• третий — классом миллионов,
• четвертый — классом миллиардов и т. д.

разряды

В каждом классе три разряда — единицы, десятки и сотни.

пример

Чтобы прочитать число $165378964535$, разобьем его справа налево на группы по три цифры. Вот так: $\textcolor{lightblue}{165} \space \textcolor{darkgreen}{378} \space \textcolor{orange}{964} \space \textcolor{coral}{535}$. Теперь можно его прочесть:

$\textcolor{lightblue}{165}$ миллиардов, $\textcolor{darkgreen}{378}$ миллионов, $\textcolor{orange}{964}$ тысячи, $\textcolor{coral}{535}$.

{"questions":,"placeholder":0,"answer":0}}}]}

Действия с натуральными числами

С натуральными числами можно производить следующие вычисления: сложение, вычитание, умножение и деление.

Сложение:

слагаемое + слагаемое = сумма

2 + 4 = 6

14 + 3 = 17

25 + 14 = 39

Кстати, если хотите дать ребёнку возможность потренироваться в сложении, предложите ему позаниматься на образовательной платформе iSmart. Здесь много разных интересных заданий, которые помогут лучше разобраться в арифметических действиях и надежно закрепить их в памяти.

Вычитание:

уменьшаемое — вычитаемое = разность

5 — 3 = 2

19 — 7 = 12

43 — 41 = 2

Потренироваться в вычитании можно на платформе iSmart.

Умножение:

множитель х множитель = произведение

5 х 3 = 15

12 х 4 = 48

17 х 23 = 391

Чтобы улучшить навыки умножения, загляните на платформу iSmart.

Деление: 

делимое : делитель = частное

8 : 2 = 4

27 : 3 = 9

64 : 32 = 2

Навыки деления также можно совершенствовать на платформе iSmart.

Примечание: если уменьшаемое число будет равно вычитаемому, то в итоге получится ноль. Если уменьшаемое число будет меньше вычитаемого, то в итоге получится отрицательное число. Ноль и отрицательное число не являются натуральными числами. 

Это же касается деления: если делимое меньше делителя, то в результате мы получим не целое, а дробное число.

Поэтому в результате сложения и умножения мы всегда получаем натуральные числа, а в результате вычитания и деления — как натуральные, так и не натуральные.

Разряды чисел.

Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.

Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.

Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда
.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда.
Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.

Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.

Такой разбор числа называется разрядным составом числа
.

Что такое разрядные слагаемые правило

Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

С помощью десяти цифр можно записать любое натуральное число.

От количества знаков (цифр) в числе зависит его название.

Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — 1, наибольшее — 9.

Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — 10, наибольшее — 99.

Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определённое место — позицию.

Разряд — это место (позиция), на котором в записи числа стоит цифра.

Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.

Разряды отсчитываются с конца числа.

Разряд единиц — это самый младший разряд, которым заканчивается любое число.

Цифра 5 — означает 5 единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).

Разряд десятков — это разряд, который стоит перед разрядом единиц.

Цифра 5 — означает 5 десятков, если она стоит на предпоследнем месте (в разряде десятков).

Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра 5 означает 5 сотен, если она стоит на третьем месте от конца числа (в разряде сотен).

Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 (ноль).

Пример. В числе 807 содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа.

807 = 8 сотен 0 десятков 7 единиц

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.

Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.

Количественный смысл натуральных чисел

Натуральные числа используются для чего-то, что можно посчитать или пронумеровать. Например, мы можем посчитать, сколько ножек у стола, сколько учеников в классе или даже сколько орешков в пачке.

А ещё мы можем пронумеровать автобусные маршруты, билеты на спектакль или спортивные разряды. 

Сколько человек в классе? 25. Это значит, что именно столько человек должны присутствовать на уроке (если, конечно, никто не болеет).

Какой номер маршрута у автобуса? 17-й. Это значит, что в городе есть ещё как минимум шестнадцать разных маршрутов, по которым ходят автобусы. 

Натуральные числа здесь выступают как средство для нумерации. Именно в этом заключается их количественный смысл — обозначать количество того, что можно посчитать.

Числа больше триллиона

Цифра ноль играет важную роль при подсчете очень больших чисел. Это помогает отслеживать эти числа, кратные 10, потому что чем больше число, тем больше нулей требуется. В приведенной ниже таблице в первом столбце указано имя числа, во втором указано количество нулей, следующих за начальной цифрой, а в третьем указано, сколько групп из трех нулей вам потребуется для записи каждого числа.

Имя	Количество нулей	Группы (3) нулей
Десять	1	(10)
Сотня	2	(100)
Тысяча	3	1 (1000)
Десять тысяч	4	(10 000)
Сотня тысяч	5	(100,000)
Миллион	6	2 (1,000,000)
Миллиард	9	3 (1000000000)
Триллион	12	4 (1000000000000)
Квадриллион	15	5
Квинтиллион	18	6
Секстиллион	21	7
Септиллион	24	8
Октиллион	27	9
Нониллион	30	10
Decillion	33	11
Undecillion	36	12
Duodecillion	39	13
Tredecillion	42	14
Кватттуор-дециллион	45	15
Квиндециллион	48	16
Сексдециллион	51	17
Септен-дециллион	54	18
Октодециллион	57	19
Novemdecillion	60	20
Вигинтиллион	63	21
Сантиллион	303	101

Все эти нули

Таблица, подобная приведенной выше, безусловно, может быть полезна для перечисления имен всех чисел в зависимости от того, сколько в них нулей. Но может быть действительно ошеломляющим видеть, как выглядят некоторые из этих чисел. Ниже приведен список, включающий все нули, для чисел до дециллиона, что немного больше, чем половина чисел, перечисленных в приведенной выше таблице..

Десять: 10 (1 ноль) Сотня: 100 (2 нуля) Тысяча: 1000 (3 нуля) Десять тысяч 10 000 (4 нуля) Сто тысяч 100 000 (5 нулей) Миллион 1 000 000 (6 нулей) Миллиард 1 000 000 000 (9 нулей) Триллион 1,000,000,000,000 (12 нулей) Квадриллион 1,000,000,000,000,000 (15 нулей) Квинтиллион 1,000,000,000,000,000,000 (18 нулей) Секстиллион 1,000,000,000,000,000,000,000 (21 ноль) Септиллион 1,000,000,000,000,000,000,000,000 (24 нуля) Октиллион 1 000 000 000 000 000 000 000 000 000 (27 нулей) Нониллион 1 000 000 000 000 000 000 000 000 000 000 000 (30 нулей) Дециллион 1 000 000 000 000 000 000 000 000 000 000 000 000 (33 нуля)

Нули, сгруппированные в наборы по 3

Ссылка на наборы нулей зарезервирована для групп из трех нулей, что означает, что они не актуальны для меньших чисел. Мы пишем числа с запятыми, разделяющими наборы из трех нулей, чтобы было легче читать и понимать значение. Например, вы пишете один миллион как 1000000, а не как 1000000.

В качестве другого примера гораздо проще вспомнить, что триллион записывается с четырьмя наборами по три. нулей, чем для подсчета 12 отдельных нулей. Хотя вы можете подумать, что это довольно просто, просто подождите, пока вам не придется считать 27 нулей для октиллиона или 303 нуля для сантиллиона.

Это так. тогда вы будете благодарны за то, что вам нужно запомнить только девять и 101 набор нулей соответственно.

Числа с очень большими числами нулей

Число гугол (названное Милтоном Сироттой) имеет после себя 100 нулей. Вот как выглядит гугол, включая все необходимые ему нули:

10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

Как вы думаете, это число большое? Как насчет гуголплекса , который представляет собой единицу, за которой следует гугол нулей. Гуголплекс настолько велик, что пока не имеет смысла – он больше, чем количество атомов во Вселенной.

Миллион и миллиард : Некоторые отличия

В Соединенных Штатах, а также во всем мире в области науки и финансов миллиард равен 1 000 миллионам, что записывается как единица с девятью нулями. Это также называется «короткой шкалой».

Существует также «длинная шкала», которая используется во Франции и ранее использовалась в Соединенном Королевстве. , в котором миллиард означает один миллион миллионов. Согласно этому определению миллиарда, число записывается с единицей, за которой следуют 12 нулей. Краткая шкала и длинная шкала были описаны французским математиком Женевьевой Гитель в 1975 году..

Можно ли умножать на пустоту

Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

• Если съесть по два яблока пять раз, то съедено 2?5 = 2+2+2+2+2 = 10 яблок
• Если их съесть по два трижды, то съедено 2?3 = 2+2+2 = 6 яблок
• Если съесть по два яблока ноль раз, то не будет съедено ничего — 2?0 = 0?2 = 0+0 = 0

Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.

Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль – это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.

Расскажу тебе позволь,

Чтобы не делил на 0!

Режь 1 как хочешь, вдоль,

Только не дели на 0!

obrazovanie.guru

Как правильно произносить числа с разрядом десятков тысяч?

Числа с разрядом десятков тысяч произносятся с учетом особенностей русского языка и правил чтения числительных. Для правильного произношения таких чисел необходимо знать следующие правила и примеры.

В числительных до 20 необходимо учитывать первую цифру в числе, которая соответствует десяткам:

1. 10 000 — «десять тысяч«;
2. 11 000 — «одиннадцать тысяч«;
3. 12 000 — «двенадцать тысяч«;
4. 13 000 — «тринадцать тысяч«;
5. 14 000 — «четырнадцать тысяч«;
6. 15 000 — «пятнадцать тысяч«;
7. 16 000 — «шестнадцать тысяч«;
8. 17 000 — «семнадцать тысяч«;
9. 18 000 — «восемнадцать тысяч«;
10. 19 000 — «девятнадцать тысяч«;
11. 20 000 — «двадцать тысяч«.

От 21 до 99 первая цифра произносится соответственно для десятков:

1. 21 000 — «двадцать одна тысяча«;
2. 32 000 — «тридцать две тысячи«;
3. 43 000 — «сорок три тысячи«;
4. 54 000 — «пятьдесят четыре тысячи«;
5. 65 000 — «шестьдесят пять тысяч«;
6. 76 000 — «семьдесят шесть тысяч«;
7. 87 000 — «восемьдесят семь тысяч«;
8. 98 000 — «девяносто восемь тысяч«;
9. 99 000 — «девяносто девять тысяч«.

Примеры приведенных выше числительных демонстрируют произношение чисел с разрядом десятков тысяч в соответствии с правилами.

Натуральный ряд

Натуральный ряд — это последовательность всех натуральных чисел, расположенных в порядке возрастания. В натуральном ряду каждое последующее число равно предыдущему + 1. 

Примеры натуральных рядов:

1, 2, 3, 4, 5, 6, 7

34, 35, 36, 37, 38, 39, 40, 41

122, 123, 124

Если разница между натуральными числами больше единицы или если последующее натуральное число меньше предыдущего, эта последовательность не является натуральным рядом.

Примеры ненатуральных рядов:

9, 10, 12, 13

47, 46, 48, 49

Практика:

Предложите ребёнку определить, какие из приведённых ниже последовательностей можно отнести к натуральным рядам:

а) 56, 57, 59, 60

б) 108, 109, 110, 111, 112, 113

в) 74, 73, 72, 71, 70

г) 6, 7, 8, 9, 10, 11, 12, 13

Примеры использования разряда десятков тысяч

Разряд десятков тысяч используется для отображения чисел, которые содержат от 10 000 до 99 999. Этот разряд находится перед разрядом тысяч и обозначает количество десятков тысяч в числе.

Вот несколько примеров чисел, где разряд десятков тысяч играет значимую роль:

• 32 546 — здесь число 3 означает, что есть 3 разряда десятков тысяч. Это число можно прочитать как «тридцать две тысячи пятьсот сорок шесть».
• 47 892 — здесь число 4 означает, что есть 4 разряда десятков тысяч. Это число можно прочитать как «сорок семь тысяч восемьсот девяносто два».
• 99 999 — это самое большое число в разряде десятков тысяч. Оно можно прочитать как «девяносто девять тысяч девятьсот девяносто девять».

Разряд десятков тысяч помогает нам определить, сколько тысяч содержится в числе и упрощает чтение больших чисел. Он также используется в математических операциях и в счетных методах.

Значение разряда десятков тысяч в числах

Разряд десятков тысяч — это позиция числа, которая находится перед разрядом тысяч

Он определяет количество десятков тысяч в числе и имеет важное значение при чтении и записи больших чисел

Каждая цифра в разряде десятков тысяч представляет собой умножение числа на 10 в пятой степени. Таким образом, значение цифры в разряде десятков тысяч увеличивается в 10 000 раз по сравнению со значением цифры в разряде тысяч.

Например, в числе 52 345 разряд десятков тысяч содержит цифру 2. Это означает, что в числе содержится 2 десятка тысяч.

Разряд десятков тысяч используется для обозначения больших чисел, таких как годы, население городов и т. д. Он помогает упростить запись и чтение чисел, делая их более понятными и удобными для использования.

Найдем двухзначное число в котором число единиц на 8 больше чем число десятков

Давайте следовать составленному алгоритму и вспомним понятие двухзначного числа в математике.

Двухзначными числами в математике называются числа, которые состоят из двух цифр.

Это цифры от 10 до 99.

Двухзначное число состоит из разряда единиц, которые принимают значение от 0 до 9 и десятков — они принимают значение от 10, 20, 30 до 90.

Введем переменные обозначив за a число десятков, а за b число единиц.

То есть наше число должно иметь вид ab.

В условии сказано, что число единиц должно быть больше на 8 числа десятков.

С помощью введенных переменных это можно записать так:

то есть: b – a = 8.

В результате мы получили уравнение с двумя переменными.

Решать уравнение будем методом подбора.

Числа a и b могут принимать значения от 0 до 9.

Под это условие подходит только число такая комбинация единиц и десятков как:

Кто в итоге прав

Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй. Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!

Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.

Это интересно: Как найти разность чисел в математике?