Вершина угла: что это значит

Содержание

• 1 Правильные пятиугольники
  • 1.1 Вывод формулы площади
  • 1.2 Inradius
  • 1.3 Хорды ​​от описанной окружности к вершины
  • 1.4 Точка на плоскости
  • 1.5 Построение правильного пятиугольника
    • 1.5.1 Метод Ричмонда
    • 1.5.2 Круги Карлайла
    • 1.5.3 Использование t ригонометрия и теорема Пифагора
    • 1.5.4 † Доказательство того, что cos 36 ° = 1 + 5 4 {\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}
    • 1.5.5 Задана длина стороны
  • 1.6 Метод Евклида
  • 1.7 Физические методы
  • 1.8 Симметрия
• 2 Равносторонние пятиугольники
• 3 Циклические пятиугольники
• 4 Общие выпуклые пятиугольники
• 5 Графики
• 6 Примеры пятиугольников
  • 6.1 Растения
  • 6.2 Животные
  • 6.3 Минералы
  • 6.4 Искусственные
• 7 Пентагонов в мозаике
• 8 Пентагонов в многогранниках
• 9 См. Также
• 10 Встроенные примечания и ссылки
• 11 Внешние ссылки

Как определить стороны пятиугольника?

Для определения сторон пятиугольника, необходимо провести измерение каждого отрезка, соединяющего соседние вершины

При измерении важно соблюдать правило округления до определенного числа знаков после запятой

Как правило, в геометрии для обозначения сторон пятиугольника используется такая нотация: AB, BC, CD, DE и EA, где A, B, C, D и E — вершины пятиугольника.

Вычисление длин сторон пятиугольника может быть полезным в различных аспектах: от расчета площади и периметра фигуры до определения углов пятиугольника с помощью теоремы косинусов.

Зная длины сторон пятиугольника, можно также проверить, является ли он правильным или неправильным. Правильный пятиугольник имеет все стороны одинаковой длины, а неправильный пятиугольник – стороны разной длины.

Как видно, определение сторон пятиугольника является важным шагом в изучении и анализе этого многоугольника, что позволяет получить информацию о его геометрических свойствах и характеристиках.

Геометрическое определение вершин пятиугольника

Каждая вершина пятиугольника имеет координаты в двумерной плоскости. Для того чтобы определить вершину пятиугольника, необходимо знать координаты точек, образующих его стороны. Зная эти координаты, можно легко вычислить координаты вершин пятиугольника.

Вершины пятиугольника можно расположить на плоскости по разным правилам. Например, если пятиугольник является правильным, то все его стороны имеют одинаковую длину, а его вершины равноудалены друг от друга. В этом случае, можно использовать геометрическую формулу для определения координат вершин правильного пятиугольника.

Определение вершин пятиугольника является важным шагом при решении геометрических задач, связанных с этой фигурой. Зная координаты вершин, можно определить свойства пятиугольника, например, его периметр, площадь или длину его сторон. Это позволяет проводить анализ и сравнение различных пятиугольников и использовать их в различных приложениях, таких как архитектура, дизайн и наука.

Литература

• Thomas L. Heath. The Thirteen Books of Euclid’s Elements. — 2nd ed. — New York: Dover Publications, 1956. — ISBN v1: 0-486-60088-2 , v2: 0-486-60089-0 , v3: 0-486-60090-4. (Аутентичный перевод книги Евклида «Начала» с обширными историческими исследованиями и детальными комментариями по тексту книги.)
• Lanru Jing, Ove Stephansson. Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications. — 2007. — ISBN 978-0-444-82937-5.
• Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
• Introduction to the Mathematics of Quasicrystals / M.V. Jaric. — Academic Press, 1989.. — Т. 2. — (Aperiodicity and Order). — ISBN 0-12-040602-0.
• Alexander I. Bobenko, Peter Schröder, John M. Sullivan, . Discrete differential geometry. — Birkhäuser Verlag AG, 2008. — ISBN 978-3-7643-8620-7.
• Satyan Devadoss, Joseph O’Rourke. Discrete and Computational Geometry. — Princeton University Press, 2011. — ISBN 978-0-691-14553-2.
• Martin Christen Clockworkcoders Tutorials: Vertex Attributes. — Khronos Group, 2009.

Презентация на тему: » УГОЛ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых.» — Транскрипт:

1

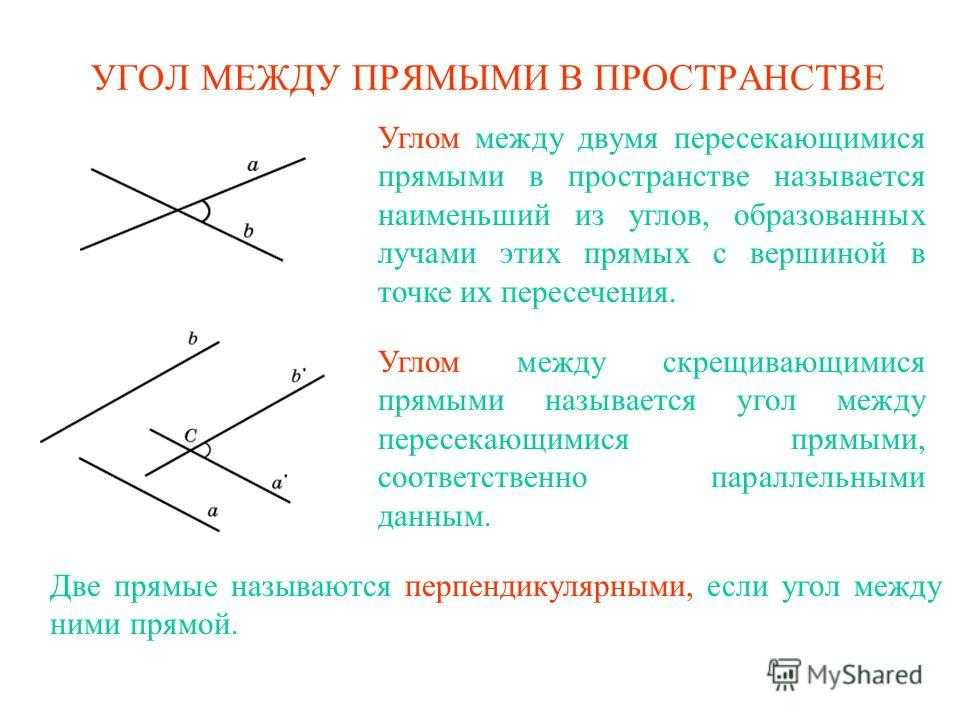
УГОЛ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным. Две прямые называются перпендикулярными, если угол между ними прямой.

2

Дана прямая в пространстве, на ней взята точка. Сколько можно построить прямых, проходящих через эту точку и перпендикулярных данной прямой? Ответ: Бесконечно много. Упражнение 1

3

Даны прямая и точка вне ее. Сколько можно построить прямых, проходящих через эту точку и перпендикулярных данной прямой? Ответ: Бесконечно много. Упражнение 2

4

Даны плоскость и параллельная ей прямая. Сколько прямых, перпендикулярных этой прямой, можно провести в данной плоскости? Ответ: Бесконечно много. Упражнение 3

5

Из планиметрии известно, что две прямые, перпендикулярные третьей прямой, параллельны. Верно ли это утверждение для стереометрии? Ответ: Нет. Упражнение 4

6

Чему равен угол между пересекающимися ребрами: а) куба; б) правильного тетраэдра? Ответ: а) 90 о ; Упражнение 5 б) 60 о.

7

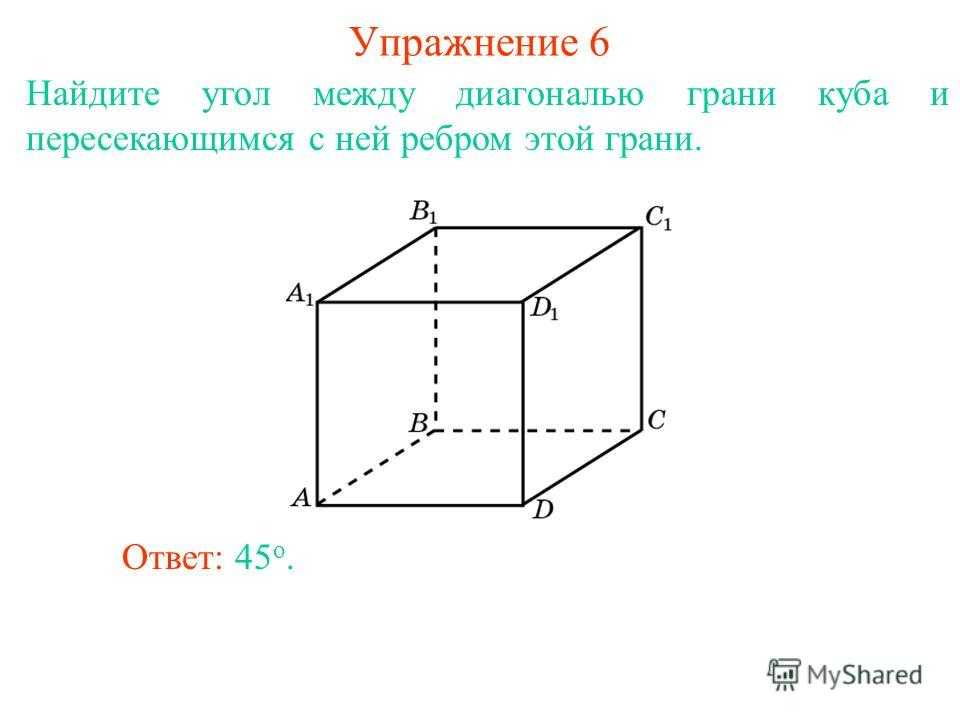
Найдите угол между диагональю грани куба и пересекающимся с ней ребром этой грани. Ответ: 45 о. Упражнение 6

8

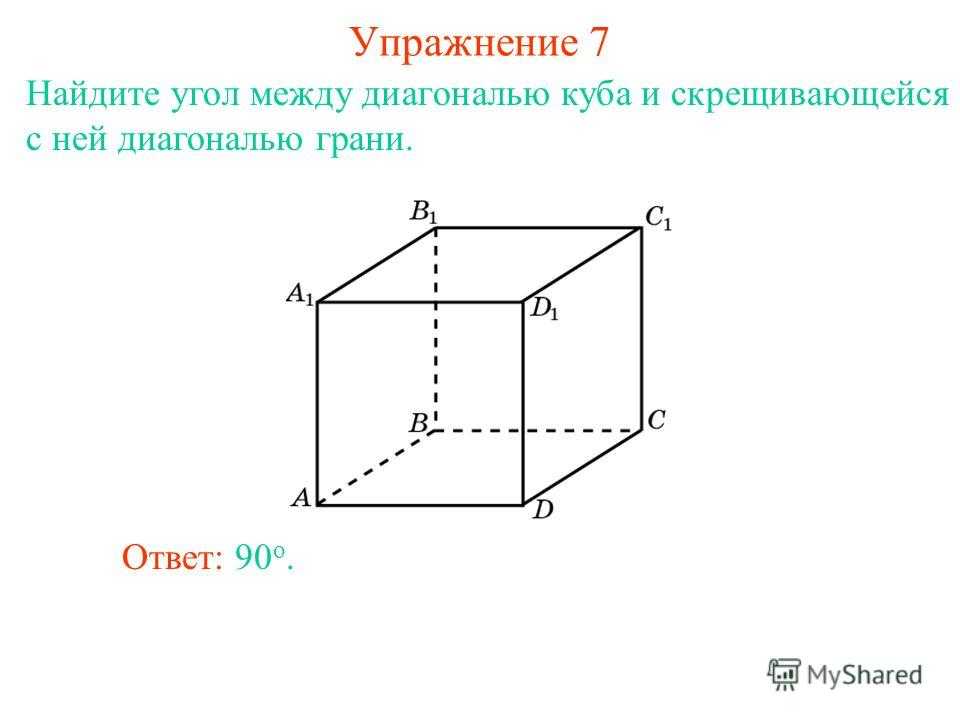
Найдите угол между диагональю куба и скрещивающейся с ней диагональю грани. Ответ: 90 о. Упражнение 7

9

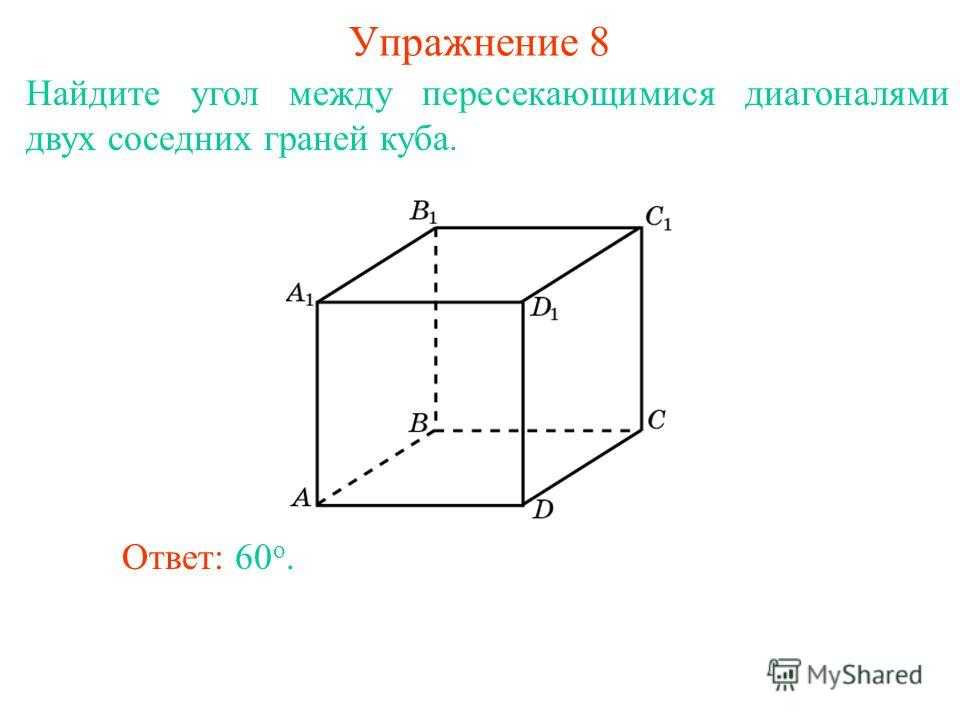
Найдите угол между пересекающимися диагоналями двух соседних граней куба. Ответ: 60 о. Упражнение 8

10

Найдите угол между диагональю куба и пересекающим ее ребром куба. Упражнение 9 Ответ:

11

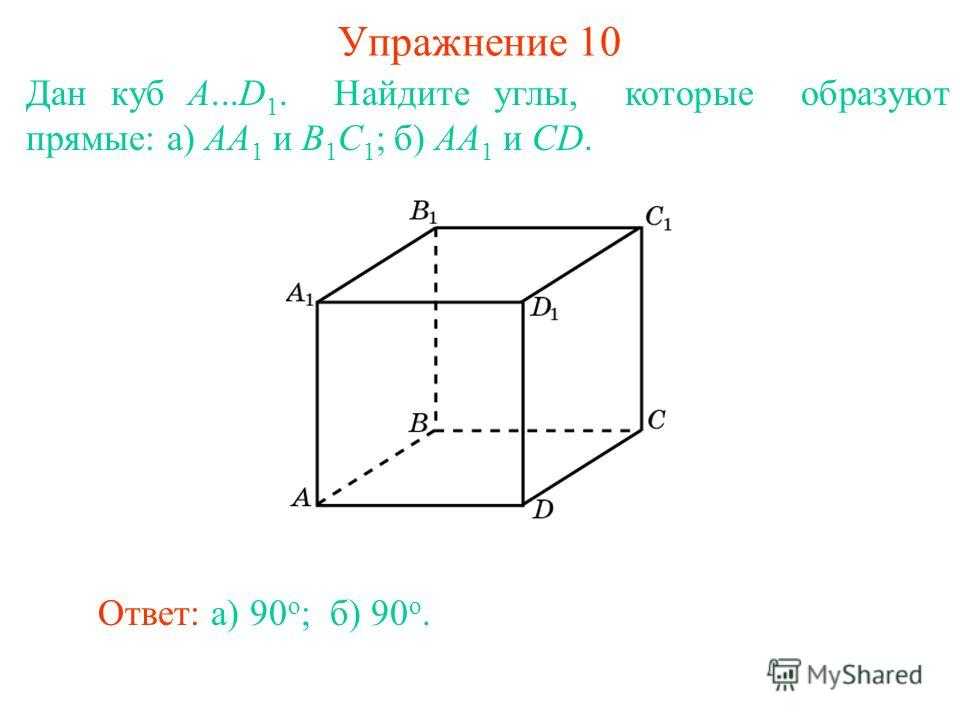
Дан куб A…D 1. Найдите углы, которые образуют прямые: а) AA 1 и B 1 C 1 ; б) AA 1 и CD. Упражнение 10 Ответ: а) 90 о ;б) 90 о.

12

В кубе A…D 1 найдите углы между прямыми: а) AD и A 1 C 1 ; б) AC 1 и DD 1 ; в) AB 1 и BC 1. Упражнение 11 Ответ: а) 45 о ;б)в) 60 о.

13

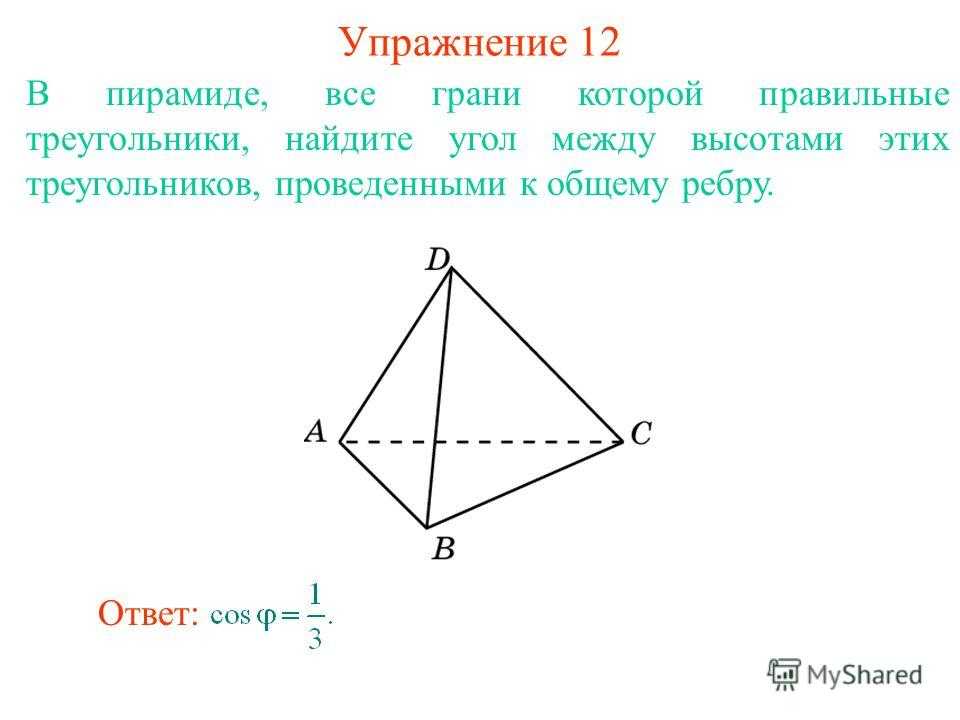
В пирамиде, все грани которой правильные треугольники, найдите угол между высотами этих треугольников, проведенными к общему ребру. Упражнение 12 Ответ:

14

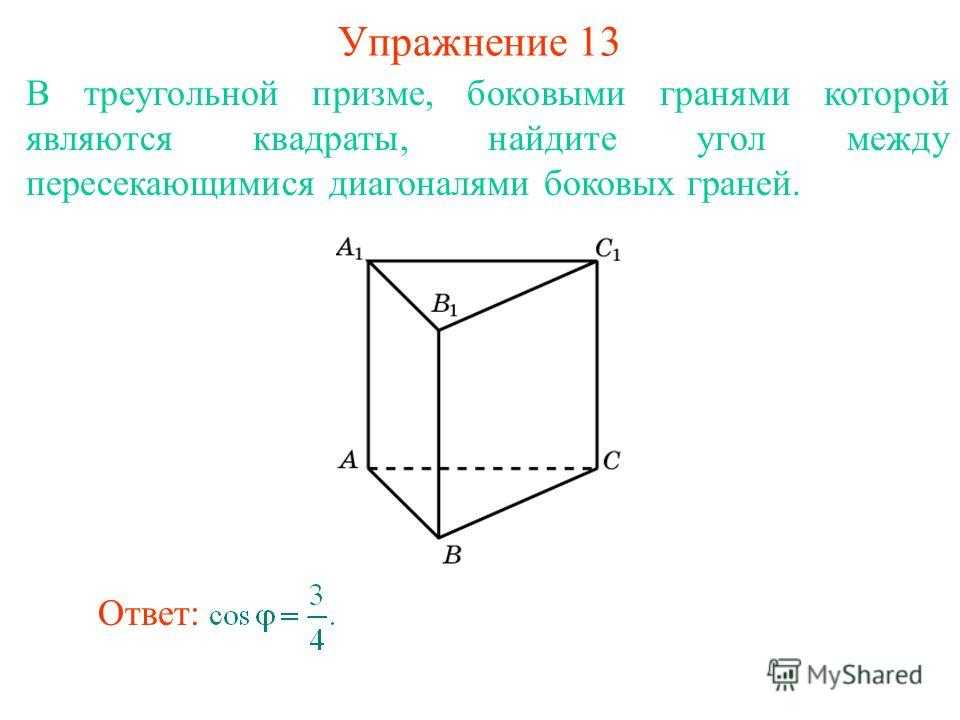
В треугольной призме, боковыми гранями которой являются квадраты, найдите угол между пересекающимися диагоналями боковых граней. Упражнение 13 Ответ:

15

В правильной четырехугольной пирамиде со стороной основания, равной боковому ребру, найдите угол между стороной основания и скрещивающимся с ней боковым ребром. Упражнение 14 Ответ: 60 o.

16

A, B, C — точки на попарно перпендикулярных лучах OA, OB, OC. Найдите углы треугольника ABC, если известно, что OA=OB=OC. Упражнение 15 Ответ: 60 o.

17

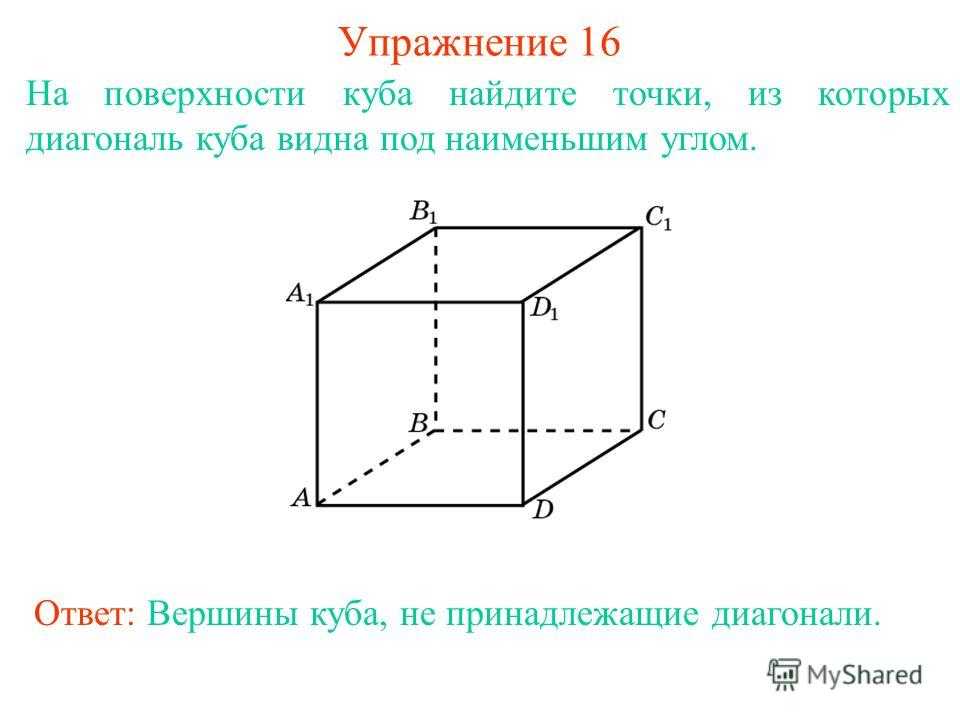
На поверхности куба найдите точки, из которых диагональ куба видна под наименьшим углом. Упражнение 16 Ответ: Вершины куба, не принадлежащие диагонали.

Пятиугольник, выпуклый и невыпуклый пятиугольник:

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).

Пятиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

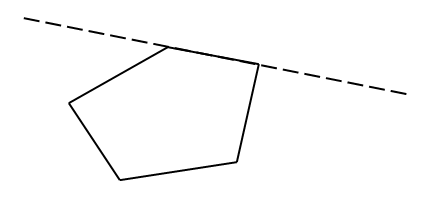
Рис. 1. Выпуклый пятиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 540°.

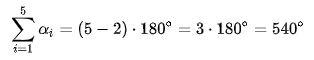
Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.

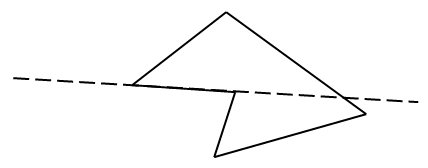
Рис. 2. Невыпуклый пятиугольник

Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.

Пентагон, выложенный плиткой

Самая известная упаковкаструктура с двойной решеткой

Правильный пятиугольник не может появляться ни в одной мозаике правильных полигоны

Во-первых, чтобы доказать, что пятиугольник не может образовывать правильную мозаику (в которой все грани конгруэнтны, что требует, чтобы все многоугольники были пятиугольниками), обратите внимание, что 360 ° / 108 ° = 3 ⁄ 3 (где 108 ° — внутренний угол), который не является целым числом; следовательно, не существует целого числа пятиугольников, разделяющих одну вершину и не оставляющих промежутков между ними. Сложнее доказать, что пятиугольник не может быть ни в какой мозаике от края до края, образованной правильными многоугольниками:

Максимальная известная плотность упаковки правильного пятиугольника составляет приблизительно 0,921, что достигается с помощью показана упаковка с двойной решеткой. В препринте, выпущенном в 2016 году, Томас Хейлз и Веден Куснер объявили о доказательстве того, что двойная решетчатая упаковка правильного пятиугольника (которую они называют упаковкой «пятиугольного ледяного луча», и что они прослеживают до работы китайских мастеров в 1900 году) имеет оптимальную плотность среди всех упаковок правильных пятиугольников в плоскости. По состоянию на 2020 год их доказательства еще не рецензировались и не публиковались.

Не существует комбинаций правильных многоугольников с 4 или более пересекающимися в вершине, содержащими пятиугольник. Для комбинаций с 3, если 3 многоугольника встречаются в вершине и один имеет нечетное количество сторон, другие 2 должны быть конгруэнтными. Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 °. Чтобы найти количество сторон этого многоугольника, результат: 360 / (180 — 126) = 6 ⁄ 3, что не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.

Существует 15 классов пятиугольников, которые могут . Ни один из пятиугольников не обладает какой-либо симметрией в целом, хотя у некоторых есть особые случаи с зеркальной симметрией.

15 одноугольных пятиугольных плиток

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

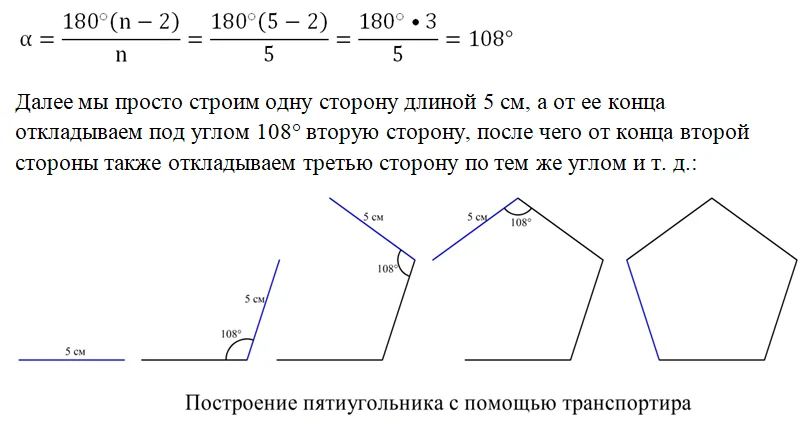
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

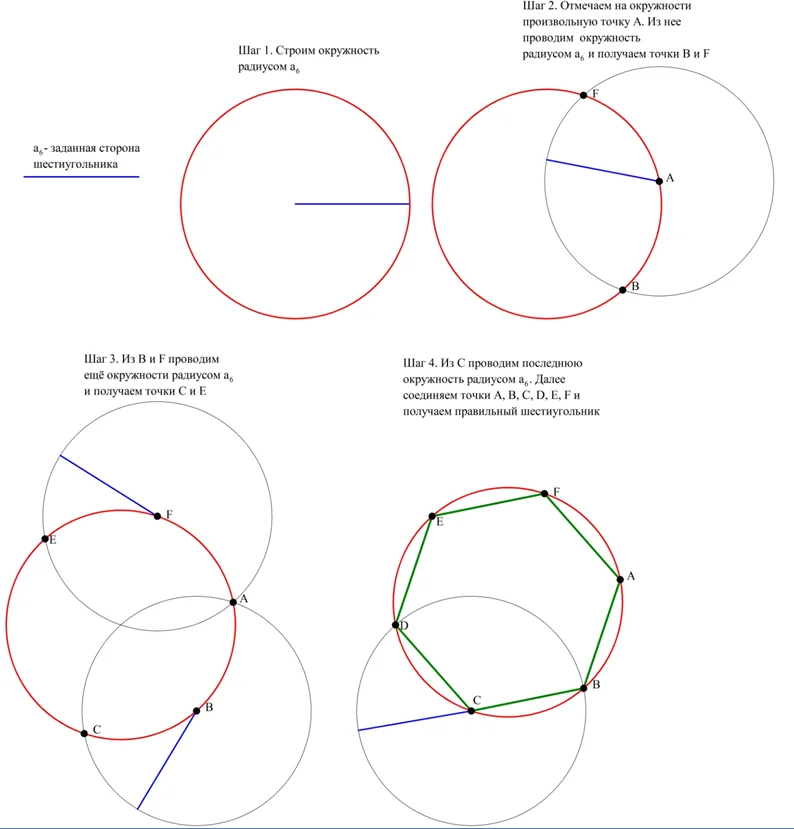
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

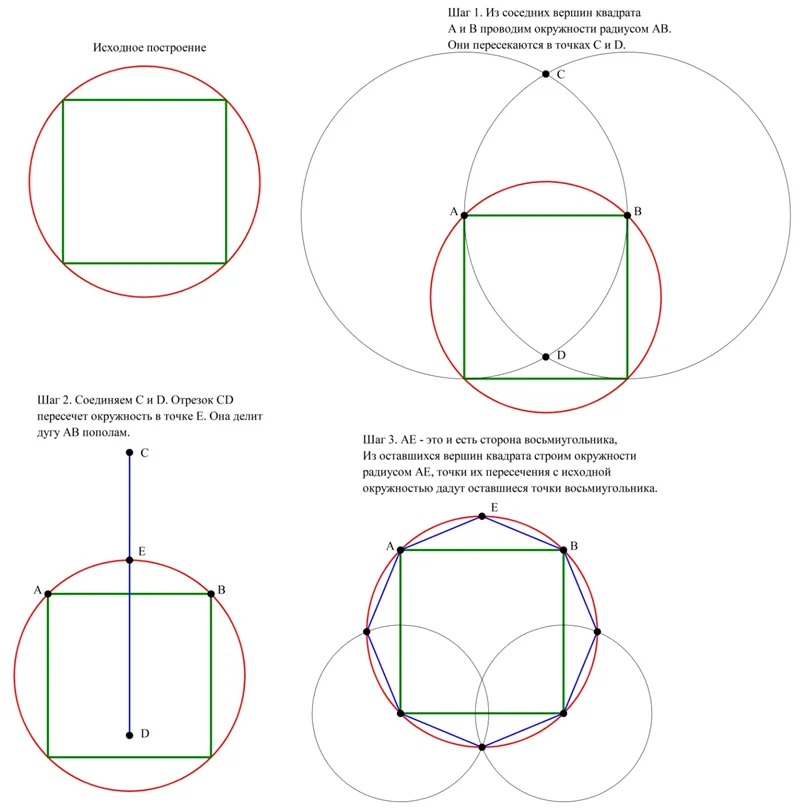
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах

Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности

Понятие многогранника

Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.

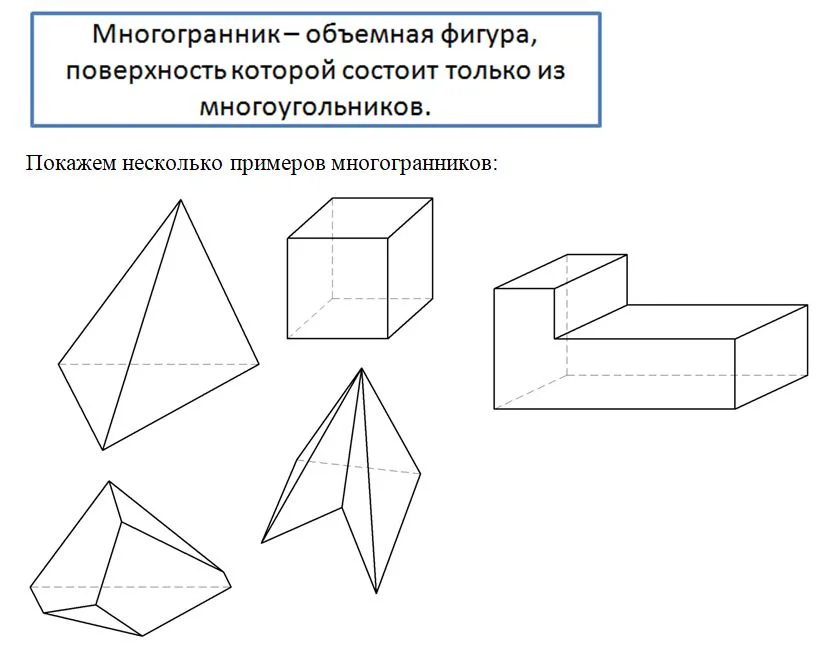
Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».

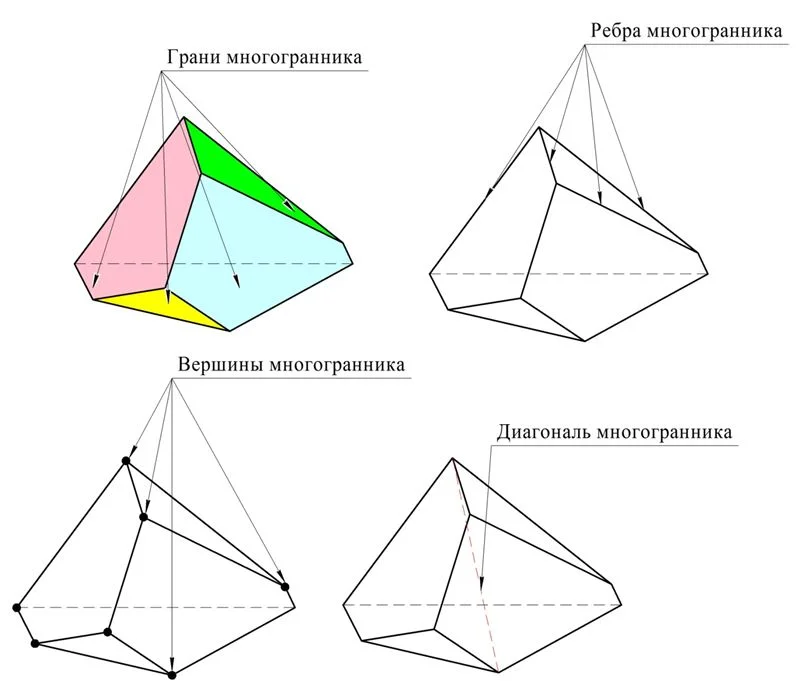
Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.

Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника

Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу

Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:

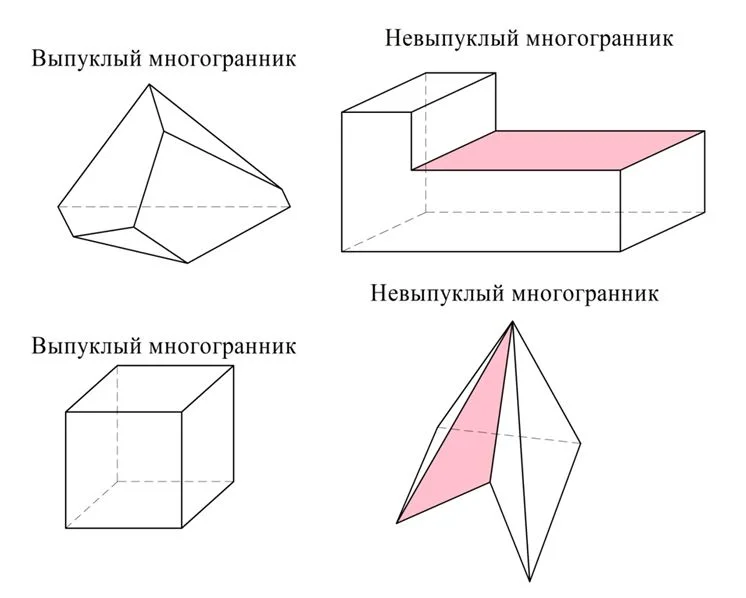
На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.

Определение [ править ]

Угла

Вершина угла — это конечная точка, в которой соединяются две линии или лучи.

Вершина из угла в точку , где два начинают или встречаться, где два отрезка присоединиться или встретиться, где две линии пересекаются (крест), или любой подходящей комбинации лучей, отрезков и линий , которые приводят две прямые «стороны» Встреча в одном месте.

Многогранника

Вершина является угловой точкой многоугольника , многогранника или других Многомерным многогранника , образованным пересечением из ребер , граней или граней объекта.

В многоугольнике вершина называется « выпуклой », если внутренний угол многоугольника (т. Е. Угол, образованный двумя ребрами в вершине с многоугольником внутри угла) меньше π радиан (180 °, два прямых угла ); в противном случае его называют «вогнутым» или «рефлекторным». В более общем смысле, вершина многогранника или многогранника является выпуклой, если пересечение многогранника или многогранника с достаточно малой сферой с центром в вершине выпукло, и вогнутым в противном случае.

Вершины многогранника связаны с вершинами графов в том смысле , что 1-скелет многогранника является графом, вершины которого соответствуют вершинам многогранника , и в этом случае граф можно рассматривать как одномерный симплициальный комплекс, вершинами которого являются вершины графа.

Однако в теории графов у вершин может быть меньше двух инцидентных ребер, что обычно недопустимо для геометрических вершин. Существует также связь между геометрическими вершинами и вершинами кривой , ее точками крайней кривизны: в некотором смысле вершины многоугольника являются точками бесконечной кривизны, и если многоугольник аппроксимируется гладкой кривой, будет точка крайней кривизны около каждой вершины многоугольника. Однако гладкая кривая, аппроксимирующая многоугольник, также будет иметь дополнительные вершины в точках, где его кривизна минимальна.

Планировки плоскости править

Вершина мозаики плоскости или мозаики — это точка, в которой встречаются три или более плиток; обычно, но не всегда, плитки мозаики являются многоугольниками, а вершины мозаики также являются вершинами ее плиток. В более общем смысле тесселяцию можно рассматривать как своего рода топологический комплекс ячеек , как и грани многогранника или многогранника; вершины других видов комплексов, таких как симплициальные комплексы, являются его нульмерными гранями.

Примеры из реальной жизни пятиугольников

Пятиугольники встречаются в разных областях нашей жизни и природы. Вот некоторые примеры:

1. Здания: В архитектуре пятиугольники могут использоваться в качестве основы для дизайна зданий. Например, пятиугольные комнаты могут предоставлять удобство и эстетичность.

2. Растения: Некоторые растения, такие как младеницы и цветок «Радуга», имеют пятиугольные формы цветков или листьев.

3. Знаки дорожного движения: Некоторые знаки на дороге, такие как знак «Конец зоны ограниченной видимости», имеют форму пятиугольника.

4. Упаковка: Пятиугольные упаковки могут использоваться для создания необычных контейнеров или упаковки подарков, которые выделяются.

5. Музыка: В музыкальной нотации пятиугольники используются для обозначения острия стрелки, указывающего на паузу в музыкальной композиции.

Это лишь несколько примеров, которые демонстрируют, что пятиугольники обычно встречаются не только в математике, но и в реальной жизни. Они придают уникальность и красоту вокруг нас.

Теорема Эйлера

У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?

Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:

4 + 4 — 6 = 2

Если выполнить такие же действия для параллелепипеда, то снова получится двойка:

6 + 8 — 12 = 2

Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:

Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.

Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?

Решение. Запишем теорему Эйлера:

Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?

Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:

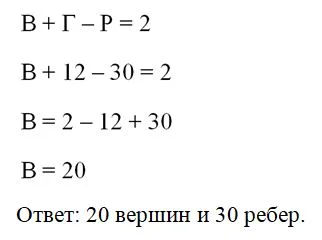
Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?

Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:

Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?

Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:

Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:

Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.

Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.

Определение пятиугольника

Пятиугольник — это геометрическая фигура, которая состоит из пяти вершин и пяти сторон. Все стороны пятиугольника равны между собой, а углы при вершинах составляют 108 градусов.

Пятиугольник является одним из видов многоугольников, которые имеют более двух вершин и сторон. Он также называется пятиугольным полигоном.

У пятиугольника общая длина его сторон суммируется, чтобы получить его периметр. Периметр пятиугольника можно найти, сложив длины всех его сторон. Чтобы найти площадь пятиугольника, необходимо знать длину его сторон и использовать соответствующую формулу.

Расположение вершин пятиугольника может быть разным. На рисунке ниже показан пример пятиугольника с указанием вершин и сторон:

Пятиугольники можно классифицировать в зависимости от различных параметров, например, в выпуклые или невыпуклые, правильные или неправильные. Правильный пятиугольник — это пятиугольник, у которого все стороны и углы равны. Неправильный пятиугольник — это пятиугольник, у которого стороны и/или углы не равны.

Примеры неправильных пятиугольников:

• Пятиугольник с разными длинами сторон;
• Пятиугольник с углами, не равными 108 градусам;
• Пятиугольник с пересекающимися сторонами.

Примеры правильных пятиугольников:

• Пентагон;
• Звезда с пятью равными сторонами;
• Построенный с использованием геометрического инструмента «компас».

Изучение свойств и характеристик пятиугольников является важной задачей в геометрии и имеет широкое применение в различных областях, таких как архитектура, дизайн, инженерия и т. д

Определение геометрической фигуры

Геометрическая фигура — это совокупность определенных элементов, таких как стороны, углы, вершины, которые образуют определенную форму в двухмерном или трехмерном пространстве.

В геометрии существует множество различных фигур, каждая из которых имеет свои особенности и характеристики. Одной из таких фигур является пятиугольник.

Пятиугольник — это геометрическая фигура, состоящая из пяти отрезков, соединенных последовательно в плоскости друг с другом. У пятиугольника есть пять сторон, пять вершин и пять углов.

Название «пятиугольник» уже указывает на то, сколько у него вершин — пять. Вершины пятиугольника образуются там, где соединяются две стороны.

Форма пятиугольника

Пятиугольник — это многоугольник, который состоит из пяти вершин и пяти сторон.

Чтобы определить, сколько вершин у пятиугольника, достаточно просмотреть его форму. В данном случае, пятиугольник имеет пять вершин.

Форма	Количество вершин
Треугольник	3
Четырехугольник	4
Пятиугольник	5

Таким образом, пятиугольник имеет пять вершин.

Задание стиля многоугольника

У любого простого -вершинного многоугольника всегда существует триангуляция, причём количество треугольников в ней независимо от самой триангуляции. В общем случае в произвольном -угольнике всего возможных вариантов построения диагоналей. Для некоторых классов многоугольников предыдущую оценку можно улучшить. Например, если многоугольник выпуклый, то достаточно лишь выбирать одну его вершину и соединять со всеми остальными, кроме его соседей.

Тогда докажем, что содержит split и merge вершины. Чтобы сделать многоугольник монотонным, нужно избавиться от split и merge вершин путём проведения непересекающихся дигоналей из таких вершин. Рассмотрим горизонтальную заметающую прямую, будем перемещать её сверху вниз вдоль плоскости на которой лежит исходный многоугольник. Будем останавливать её в каждой вершине многоугольника.

Как определяется угол?

Угол — это фигура, образованная двумя полупрямыми, которые начинаются в одной точке, называемой вершиной угла. Каждая из полупрямых называется стороной угла.

Углы могут быть заданы по различным параметрам – мерой угла, его видом или по расположению сторон относительно друг друга.

1. Мера угла определяется в градусах, минутах и секундах. Обычно принято измерять углы в градусах, где один полный оборот равен 360 градусам.
2. Вид угла может быть острый, прямой, тупой, полный или коллинеарный.
3. Расположение сторон относительно друг друга может быть параллельным или пересекающимся.

Определение угла имеет большое применение в различных областях, включая геометрию, физику, инженерию и архитектуру.

Основная вершина [ править ]

Вершина B — это ухо, потому что открытый отрезок линии между C и D полностью находится внутри многоугольника. Вершина C — это рот, потому что открытый отрезок линии между A и B полностью находится за пределами многоугольника.

Вершина многоугольника x _i простого многоугольника P является главной вершиной многоугольника, если диагональ [ x _{(i — 1)} , x _{(i + 1)} ] пересекает границу P только в точках x _{(i — 1)} и x _{(i + 1)} . Есть два типа основных вершин: уши и рты .

Уши править

Основная вершина х _I простого многоугольника Р называется уха , если диагонали [ х _{(я — 1)} , х _{(г + 1)} ] , что мосты х _я целиком лежит в P . (см. также выпуклый многоугольник ) Согласно теореме о двух ушах , каждый простой многоугольник имеет как минимум два уха.

Вершины в компьютерной графике

В компьютерной графике объекты часто представляются как триангулированные многогранники , в которых вершинам объекта сопоставляются не только три пространственные координаты , но и другая необходимая для правильного построения изображения объекта графическая информация, такая как цвет, отражательная способность , текстура , нормали вершин . Эти свойства используются при построении изображения с помощью

Любая диагональ делит на два многоугольника и. За и обозначим количество вершин в и соответственно. Многоугольник является -монотонным, если в нём отсутствуют split и merge вершины.

ВЕРШИНА — ВЕРШИНА, в математике точка, в которой сходятся две стороны треугольника или другого многоугольника, либо пересекаются три и более сторон пирамиды или другого многогранника. Алгоритм точки в многоугольнике — Проверка принадлежности данной точки данному многоугольнику На плоскости даны многоугольник и точка. Многоугольник может быть как выпуклым, так и невыпуклым.

ДИАГОНАЛЬ — (греч., от dia чрез, и gonia угол). 1) прямая линия, соединяющая в прямолинейной фигуре вершины двух углов, не лежащие на одной прямой. Определение. Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех и более отрезков (звеньев). Отрезки (звенья) замкнутой ломаной линии называются сторонами многоугольника, а общие точки двух отрезков — его вершинами.

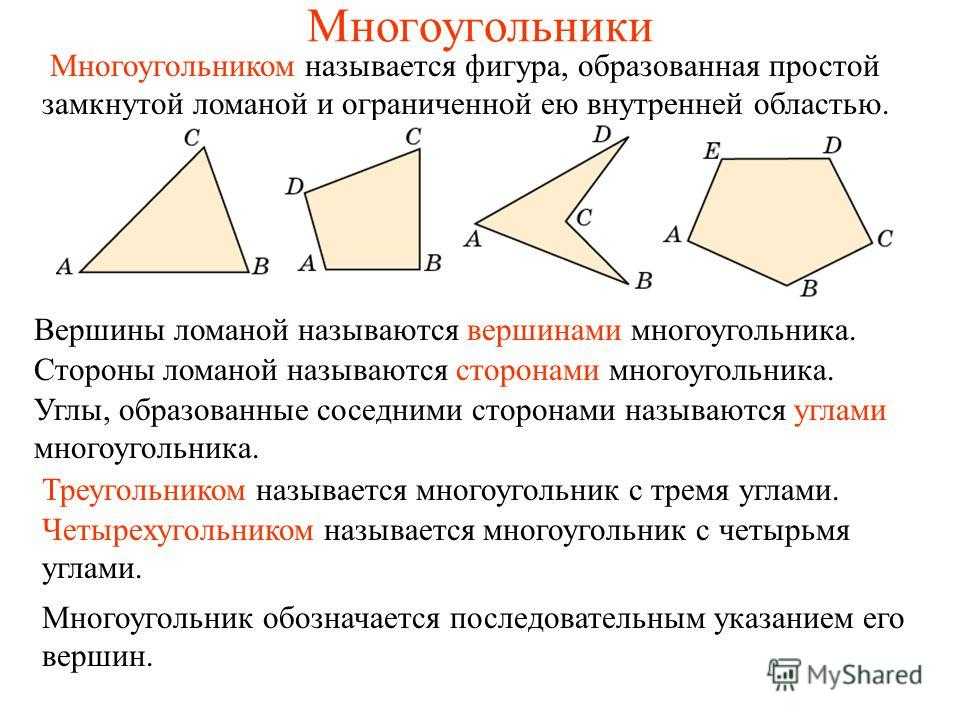
Определение. Четырехугольник — это плоская геометрическая фигура, состоящая из четырех точек (вершин четырехугольника) и четырех последовательно соединяющих их отрезков (сторон четырехугольника). У четырехугольника никогда на одной прямой не лежат три вершины. Прямоугольник — это четырехугольник, у которого все углы прямые. Многоугольником может называться замкнутая ломаная с самопресечениями и правильные звёздчатые многоугольники.