Дельта и d в физике: основные различия

Дельта в математических выражениях

Символ дельта (Δ) имеет широкое применение в математике и науке. Он происхожден из греческого алфавита и обычно используется для обозначения разности или изменения какого-то значения.

В математике дельта-обозначение может быть использовано для обозначения разности двух значений, например, Δx для разности координаты x2 и x1. Также дельта-обозначение может быть использовано для обозначения приращения функции, например, Δf для приращения функции f(x).

Дельта-обозначение также используется в физике. Например, Δt обозначает изменение времени, Δv обозначает изменение скорости, а ΔE обозначает изменение энергии.

Один из наиболее известных примеров применения дельта в физике это формула для определения delta-v, которая используется в космогонии и астрономии. Формула выглядит следующим образом: Δv = v2 — v1, где Δv — изменение скорости, v2 — конечная скорость и v1 — начальная скорость.

Дельта также может быть использована для обозначения треугольника в геометрии. Например, ΔABC означает треугольник с вершинами A, B и C.

Дельта-обозначение можно использовать как символ для обмена или вращения. Например, Δx может обозначать векторное перемещение или изменение положения объекта.

Другой вариант использования дельта-обозначения — это в области географии. Она может использоваться для обозначения изменения высоты над уровнем моря. Например, Δh может обозначать изменение высоты между двумя точками на карте.

В информатике дельта-обозначение может быть использовано для обозначения разности между двумя версиями программного обеспечения или базы данных. Например, Δx может обозначать различия между версией X и предыдущей версией.

Символ delta (Δ) также имеет альтернативный вариант записи — маленькую латинскую букву d с чертой сверху (d̄). Он используется для обозначения дифференциала, например, dx или dy.

В типографии дельта-обозначение может быть представлено в виде символа Δ или в виде латинской буквы d с чертой сверху (d̄). Чтобы вставить этот символ в текст, можно использовать соответствующий код символа: Δ — U+0394 или d̄ — U+1E0C.

Таким образом, символ дельта широко применяется в математике, физике, астрономии, географии и других наук. Он используется для обозначения разности, изменения, вращения, обмена и других величин. Объясните своим читателям, что такое дельта и как и когда она применяется в различных областях науки.

Определение и значение дельты в физике

В физике символ дельта (Δ) обычно используется для обозначения разности между двумя величинами. Он также может использоваться для обозначения изменения величины в течение определенного времени или в пределах определенного пространства.

Обозначение дельта часто используется для обозначения разности координат, времени, энергии, скорости и других физических величин. Например, ∆x обозначает изменение координаты по оси x, ∆t обозначает изменение времени, а ∆E может обозначать изменение энергии.

Определение дельта в физике очень важно, поскольку позволяет измерять и анализировать изменения величин. Он позволяет физикам изучать, как различные физические параметры изменяются во времени или пространстве и как эти изменения влияют на систему в целом

Дельта также играет важную роль в уравнениях и формулах физики. Она позволяет выразить изменение величины с помощью математического символа и использовать его для решения различных задач и уравнений.

Символ	Описание
∆x	Изменение координаты по оси x
∆t	Изменение времени
∆E	Изменение энергии
∆v	Изменение скорости

Понятие дельты

В физике термин «дельта» (обозначается греческой буквой Δ) обычно используется для обозначения изменения или разности между двумя значениями. Математически дельта обозначает разность между двумя величинами и вычисляется как разность их значений.

Дельта может быть использована для измерения изменений в различных физических величинах, таких как время, расстояние, скорость и т.д. Например, если объект движется с постоянной скоростью, дельта времени будет обозначать изменение времени, прошедшее между двумя разными моментами.

Кроме того, дельта может быть использована для обозначения разности величин, таких как разность потенциалов, разность температур или разность давления. Например, дельта температуры будет обозначать разность между начальной и конечной температурой в системе.

Дельта в физике также используется для обозначения бесконечно малых приращений или разностей. Например, дельта x может использоваться для обозначения бесконечно малого изменения координаты x.

Таким образом, понятие дельты играет важную роль в физике, позволяя измерять изменения различных физических величин и вычислять разные разности между ними.

Значение дельты в физике

Когда мы используем символ дельта, мы указываем, что что-то меняется или имеет разность. Например, дельта может обозначать изменение времени (Δt), изменение расстояния (Δd) или изменение скорости (Δv).

Дельта также может использоваться для обозначения разности между двумя значениями. Например, если у нас есть начальное значение величины (a) и конечное значение (b), мы можем обозначить разницу между ними как Δa = b — a.

Дельта является полезным символом в физике, так как позволяет нам выразить изменение или разность величин и легко обозначать их в уравнениях. Он помогает нам понять, как одно значение отличается от другого и как величины взаимосвязаны друг с другом.

Примеры использования дельты в физике

1. Скорость изменения: Дельта может быть использована для измерения скорости изменения величин, таких как скорость, ускорение или температура. Например, скорость изменения положения объекта может быть выражена как Δx/Δt, где Δx — изменение в положении объекта, а Δt — изменение во времени.

2. Разность величин: Дельта также может использоваться для измерения разности между двумя физическими величинами. Например, давление в точке A может быть обозначено как P_A, а давление в точке B — P_B. Разность между ними может быть выражена как ΔP = P_A — P_B.

3. Изменение энергии: Дельта может использоваться для измерения изменения энергии в системе. Например, изменение внутренней энергии системы может быть выражено как ΔU = U_{конечная} — U_{начальная}, где U_{конечная} — внутренняя энергия в конечном состоянии, а U_{начальная} — внутренняя энергия в начальном состоянии.

4. Разница в потенциале: Дельта также может быть использована для измерения разницы в потенциале, например, электрическом или гравитационном. Например, разница в электрическом потенциале между двумя точками A и B может быть выражена как ΔV = V_A — V_B, где V_A — электрический потенциал в точке A, а V_B — электрический потенциал в точке B.

Все эти примеры демонстрируют, как дельта используется для измерения изменений или различий в физических величинах. Она позволяет уточнить и точнее определить изменение величины, что является важным аспектом в физике и других науках.

Видео:Дельта альфа альфа штрих | МФТИСкачать

Значение дельты в лингвистике

Дельта может относиться к звуковым изменениям внутри языка, таким как звуковые сдвиги, слияния или разделения фонем, изменения в произношении. Она также может охватывать изменения в грамматике, лексике или семантике языка.

Пример использования дельты в лингвистике:

Исследователи лингвистической дельты обратили внимание на серию фонетических и морфологических изменений в диалектах региона. Они обнаружили, что звук в начале слова заменяется на , а окончание слова «-ing» превращается в «-in»

Эти изменения в диалекте являются примером лингвистической дельты, которая проявляется в звуковой системе и грамматике.

Таким образом, дельта имеет важное значение в лингвистике, помогая исследователям понять и объяснить различия между языками и языковыми вариантами. Она позволяет изучать эволюцию и развитие языка, а также углублять наше понимание его структуры и семантических особенностей

Таблица символов: оптимальное решение в любом случае

Не всегда инсталлирован на компьютере текстовый процессор «Ворд». ЭВМ может быть не подключена к глобальной паутине и копировать знак дельта просто неоткуда. А АСКИ-код этого символа не помним. Как бы получается безвыходная ситуация. Но решение есть. Причем очень простое. Достаточно использовать такую стандартную утилиту, как «Таблица символов». Для этого выполняем следующие манипуляции:

• Открываем меню «Пуск» с помощью нажатия соответствующей клавиши или кликом правой кнопки манипулятора типа мышь.
• В открывшемся списке необходимо выбрать пункт «Программы».
• На следующем этапе кликаем на надписи «Стандартные».
• Далее нужен раздел «Системные».
• Тут находим утилиту с надписью «Таблица символов».
• В списке находим нужную нам букву (заглавную Δ или прописную δ).
• Затем совершаем клик правой кнопкой мышки на кнопке «Выбрать». После этого должна активной стать другая кнопка – «Копировать». Ее и нажимаем. Затем выбранный нами символ помещается в буфер обмена.
• Далее переходим в то приложение, в котором необходимо вставить такой символ и нажимаем стандартную комбинацию «Ctrl» и «V». В качестве альтернативы можно использовать «Shift» и «Insert». Еще один способ вставки – это использование меню «Вставка» и одноименной кнопки.

В отличие от всех ранее приведенных методов, этот является универсальным и работает во всех программах под управлением такой операционной системы, как «Виндовс».

Значение дельты в физике

Одним из самых частых значений дельты является обозначение разницы или изменения величин. Например, в физике дельта часто используется для обозначения изменения положения (Δx), скорости (Δv) или времени (Δt). Она указывает на разницу между двумя значениями и позволяет рассчитать и измерить изменение величины величину.

Дельта также может использоваться для обозначения дискретности или квантования величин. В квантовой физике, например, дельта (ΔE) может обозначать энергетический уровень или разницу энергии между двумя состояниями. Также дельта может обозначать дискретность величин в дифференциальном и интегральном исчислении.

Кроме того, дельта может использоваться для обозначения конечной разности или предела, включая дифференциал и поправку. Например, дельта (Δf) может обозначать изменение функции f(x) при изменении аргумента x. Она указывает на увеличение или уменьшение значения и может быть выражена как фактическое значение или в виде производной.

Таким образом, значение дельты в физике может быть связано с изменением величины, разницей между значениями, квантованием или конечными разностями. Это важный символ, который позволяет ученым обозначать и измерять величины и свойства в различных научных и инженерных дисциплинах.

Валкнут

Три взаимосвязанных треугольника получили название от древнескандинавских слов valr (убитые воины) и knut (узел). Знак присутствует на множестве археологических объектов древних германских народов. Составное существительное valknut появилось в современную эпоху, и неизвестно, как символ назывался во время его исторического изображения.

Ученые, давая описание символа триединства валкнута, затрудняются в точной его трактовке. Некоторые связывают знак с богом Одином. Авторитетный специалист по германскому и кельтскому язычеству академик Хильда Эллис Дэвидсон считала, что фигура означала Одина в окружении его атрибутов, двух волков или воронов. Эти животные, как и валкнут, часто изображались на кремационных урнах, найденных на англосаксонских кладбищах Восточной Англии.

Так как символ присутствует рядом с изображением Одина на погребальных плитах и подношениях, то большинство специалистов считает, что знак соотносится с религиозными практиками, связанными со смертью.

Изображение применяется в современной народной культуре неоязычества. Как и другие древние символы, в наше время знак валкнут обретает новые интерпретации. Его используют различные политические и коммерческие группы, иногда изображение встречается в современной народной культуре.

Поскольку знак происходит из традиций германского язычества, его как символ своего наследия используют некоторые «белые» националистические группы. Несмотря на это, валкнут не был классифицирован немецким правительством как нежелательное изображение.

https://fb.ru/article/400566/simvol-triedinstva-znachenie-opisanie-avtor-znaka-mira-osobennosti-ispolzovaniya-vidyi-izobrajeniya-i-svyaschennyie-simvolyi

Видео по теме:

Вопрос-ответ:

Для чего нужен дельта знак в математике?

Дельта знак используется, чтобы обозначить разность двух значений какой-либо величины. Этот знак часто используется в геометрических расчетах, исследовании функций и при вычислении производных.

Как записывается дельта знак в математике?

Дельта знак выглядит как буква греческого алфавита «∆» и обычно пишется от руки, но также может быть введен в текст с помощью соответствующего символа.

Какие формулы можно решить с помощью дельта знака?

Дельта знак может быть использован для решения формул нахождения разности двух величин, таких как площадь прямоугольника и правильного многоугольника, объем и площадь поверхности шара, длина окружности и длина дуги.

Каковы правила использования дельта знака?

Правила использования дельта знака зависят от конкретной задачи. Для решения уравнений используется формула Δ=b^2-4ac (для квадратных уравнений), для расчета границ листа бумаги используется формула Δp=2(a+b), где a и b — кратности первой и второй стороны листа.

Как использовать дельта знак для нахождения производной?

Для нахождения производной функции используется формула Δf/Δx, где Δx — бесконечно малая величина, а Δf — разность значений функции f(x) при изменении аргумента x на Δx.

Можно ли применять дельта знак для решения задач статистики?

Да, дельта знак можно использовать для расчета изменения процентных показателей статистических данных. Например, Δp= (np-nq)/n*100%, где p и q — процентные показатели, n – выборка.

Можно ли использовать дельта знак при решении задач по физике?

Да, дельта знак можно использовать для расчета изменения физических величин. Например, ΔV=V2-V1 (для вычисления разности объемов), Δt=t2-t1 (для вычисления разности временных интервалов) и т.д.

Дельта знак и его значение в технике

Дельта знак – это математический символ, который используется для обозначения изменения. Однако, его использование не ограничивается только математикой и наукообразными дисциплинами. Дельта знак также широко применяется в технике.

В технике дельта знак часто используется для обозначения разности между двумя значениями. Например, дельта напряжения описывает изменение значений напряжения между двумя точками, а дельта температуры – изменение температуры между двумя моментами времени или в разных точках.

Часто дельта знак используется в технических документах и отчетах, чтобы дать понимание о том, насколько значительны изменения

И, конечно, важно уметь правильно читать и использовать дельта знак в технике

Список литературы

Дельта знак — это математический символ, который обозначает разность двух значений. Для ознакомления с его основами и примерами использования рекомендуется обратиться к следующим источникам:

• «Математический словарь». Под редакцией И. Н. Бронштейна и К. А. Семенова. — М.: Наука, 2000.
• «Курс математического анализа». Автор А. Н. Колмогоров, С. В. Фомин. — М.: Наука, 1981.
• «Математический анализ». Автор Л. Д. Кудрявцев. — М.: Наука, 2006.

В этих работах вы найдете подробное описание правил применения дельта знака в математических операциях. Также вы можете использовать онлайн-ресурсы для расчетов с дельта знаком, такие как WolframAlpha или Symbolab.

Наконец, вы можете найти много примеров использования дельта знака в вычислительной математике в научных статьях и исследовательских работах. Рекомендуется обращаться к таким журналам, как «Mathematical Proceedings of the Cambridge Philosophical Society» и «Journal of Mathematical Analysis and Applications».

Подробнее о скорости: что же это такое

Достаточно просто, не так ли? Точнее говоря (физики очень любят точность), скорость равняется изменению положения, деленному на изменение времени. Потому скорость движения вдоль оси X можно выразить следующим образом:

В реальном мире скорость может принимать очень разные формы, некоторые из них описываются в следующих разделах.

Смотрим на спидометр: мгновенная скорость

Итак, у нас уже есть общее представление о скорости. Именно ее измеряет спидометр автомобиля, не так ли? Когда вы катите по прямолинейному шоссе, все, что нужно делать, — всего лишь следить за показаниями спидометра. “Уже 140 километров в час. Пожалуй, сбросим скорость до 120”. Именно так мы часто поступаем в жизни, а иначе говоря, так мы определяем мгновенную скорость.

Движемся постоянно: равномерная скорость

А что если долгое время автомобиль едет со скоростью 120 километров в час? В физике эта скорость называется равномерной (или постоянной), а в жизни она возможна только при движении на абсолютно ровных и прямолинейных дорогах, когда долгое время можно поддерживать движение без изменения скорости.

Равномерное движение с постоянной скоростью является простейшим видом движения, поскольку оно никак не меняется.

Движемся вперед и назад: неравномерное движение

Название этого типа движения говорит само за себя: неравномерное движение означает движение со скоростью, меняющейся со временем. Именно с такой скоростью мы чаще всего сталкиваемся в повседневной жизни. Вот как выглядит уравнение изменения скорости от исходной скорости ​\( v_1 \)​ до конечной скорости ​\( v_0 \)​:

Остальная часть этой главы посвящена ускорению, которое характеризует неравномерность движения.

Жмем на секундомер и определяем среднюю скорость

Выражение со скоростями не так уж неосязаемо, как может показаться. Измерения скорости можно сделать более конкретными. Допустим, что вам хочется совершить путешествие из Нью-Йорка в Лос-Анджелес, которые находятся на расстоянии около 2781 миль друг от друга. Если предположить, на это путешествие ушло 4 суток, то какой была ваша скорость?

Скорость можно найти, если поделить пройденное расстояние на затраченное на это время:

Итак, результат 695,3 получен, но в каких единицах он выражен?

В этом выражении мили делятся на сутки, т.е. результат равен 695,3 милям в сутки. Это не совсем стандартная единица измерений и вполне естественно было бы поинтересоваться: а сколько это миль в час? Для ответа на этот вопрос нужно перевести сутки в часы, как показано в главе 2. Поскольку в сутках 24 часа, то получим следующий результат:

Итак, получен более понятный результат 28,97 миль в час. Смущает лишь столь малая величина скорости, ведь обычно машины едут со скоростью в 2-3 раза быстрее, однако среднюю скорость для всего путешествия мы вычислили, разделив все расстояния на все время, включая время отдыха.

Средняя скорость и неравномерное движение

Средняя скорость отличается от мгновенной, если только вы не движетесь равномерно, когда скорость вообще не меняется. А средняя скорость неравномерного движения, когда все расстояние делится на все время, может отличаться от мгновенной скорости.

Путешествуя из Нью-Йорка в Лос-Анджелес, вам наверняка придется провести несколько ночей в отелях, и во время вашего отдыха мгновенная скорость автомобиля равна 0 миль в час, а средняя скорость — 28,97 миль в час! Дело в том, что средняя скорость получена в результате деления всего расстояния на все время.

Средняя скорость может зависеть от фактически пройденного пути. Допустим, что, путешествуя по штату Огайо, вы решили подвезти попутчика в штат Индиана и погостить у вашей сестры в штате Мичиган. Все путешествие может иметь вид, показанный на рис. 3.3: первые 80 миль — в штат Индиана, а потом 30 миль — в штат Мичиган.

Если ехать со скоростью 55 миль в час, то для преодоления всего пути длиной 80 + 30 = 110 миль потребуется 2 часа. Но если взять расстояние по прямой между начальной и конечной точкой путешествия, которое равно 85,4 миль, то средняя скорость будет равна:

Таким образом, получена средняя скорость для расстояния от начальной до конечной точки путешествия вдоль пунктирной линии. Но если вам нужно определить скорость для каждого из двух отрезков фактически пройденного пути, то нужно измерить длину каждого из двух отрезков и разделить их на время их прохождения.

При движении с равномерной скоростью это можно сделать легко и просто, поскольку в таком случае средняя скорость равняется мгновенной скорости в любой точке пути.

Доказательства теорем об углах, связанных с окружностью

      Теорема 1. Величина равна половине величины , опирающегося на ту же дугу.

      Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является, и центральный угол AOC (рис. 5).

Рис. 5

      Так как отрезки AO и BO являются, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является AOB, то справедливы равенства

      Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

      Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6

      В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

      Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

Рис. 7

      В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

      Теорема 2. Величина угла, образованного пересекающимися, равна половине суммы величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 8.

Рис. 8

      Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – BED, а углы CDB и ABD являются , то справедливы равенства

что и требовалось доказать.

      Теорема 3. Величина угла, образованного, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 9.

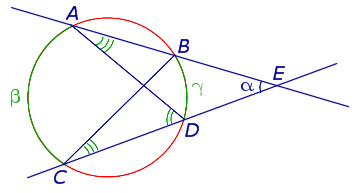
Рис. 9

      Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – ADE, а углы ADC , DCB и DAB являются , то справедливы равенства

что и требовалось доказать.

      Теорема 4. Величина угла, образованного  и   и , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

      Доказательство. Рассмотрим рисунок 10.

Рис. 10

      Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD –, проходящий через точку касания, а угол ACD – , опирающийся на диаметр, . Поэтому справедливы равенства

что и требовалось доказать

      Теорема 5. Величина угла, образованного, равна половине разности величин дуг, заключённых между сторонами этого угла.

      Доказательство. Рассмотрим рисунок 11.

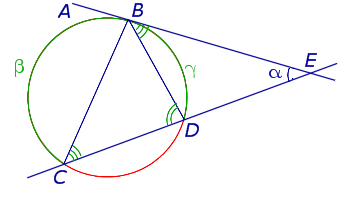
Рис. 11

      Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – DBE, а углы BDC и BCD являются . Кроме того, углы DBE и DCB, в силу , равны. Поэтому справедливы равенства

что и требовалось доказать.

      Теорема 6.Величина угла, образованного двумя, равна половине разности величин дуг, заключённых между его сторонами.

      Доказательство. Рассмотрим рисунок 12.

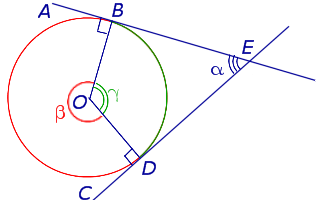
Рис. 12

      Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что . Поэтому справедливо равенство

α = π – γ .

      Далее получаем

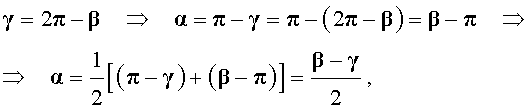
что и требовалось доказать.

Христианские варианты треугольника

В религиозной символике Средневековья появлялось много разновидностей подобных фигур:

1. Треугольник в сочетании с крестом символизировал смерть на кресте Иисуса за грехи человеческие, воскресение его Богом-Отцом, покаяние христиан и снисхождение Святого Духа.
2. Три рыбы, составляющие треугольник, означали: Иисус Христос, Сын Божий, Спаситель. Также они знаменовали Троицу.
3. Треугольник, содержащий греческие буквы Omicron, Omega и Nu. Эти буквы означают собой слова εγω ειμι ο ων, сказанные Богом Моисею из горящего куста (Исход 3:14), которые переводятся как «Я есть Сущий». Дословно фраза была взята из Септуагинты, древнегреческого перевода Ветхого Завета.
4. Три фигурки бегущих кроликов создают два треугольника, внутренний и внешний. Символ часто присутствовал как рельефный элемент архитектуры и деревянных деталей. Знак также знаменует Триединого Бога. Такое изображение встречается в настенной живописи древнего Египта и, возможно, тогда символизировало мужчину, женщину, потомство.

Диакритические знаки[править | править код]

Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.

Символ	Значение
x˙{\displaystyle {\dot {x}}}	первая производная по времени
x¨{\displaystyle {\ddot {x}}}	вторая производная по времени
x′{\displaystyle x^{\prime }}	первая производная
x′′{\displaystyle x^{\prime \prime }}	вторая производная
x→{\displaystyle {\vec {x}}}	векторная величина
x¯{\displaystyle {\bar {x}}}	среднее значение, античастица, комплексно сопряжённое
x^{\displaystyle {\hat {x}}}	оператор
x~{\displaystyle {\tilde {x}}}	подчёркивает отличие величины от предварительно принятой
x^∗{\displaystyle {\hat {x}}^{*}}
x^†{\displaystyle {\hat {x}}^{\dagger }}	оператор эрмитового сопряжения
Å	ангстрем

Роль дельта в экологии и гидрологии

Дельта представляет собой важное экологическое и гидрологическое образование, которое образуется на месте впадения реки в океан, море или озеро. В районе дельты наблюдается смешение пресной и соленой воды, что создает уникальные условия для развития редких видов растений и животных

Одной из основных ролей дельты в экологии является обеспечение биоразнообразия. Здесь обитают множество видов растений и животных, которые адаптировались к уникальным условиям этой местности. Кроме того, дельта служит убежищем и местом размножения для многих видов птиц и рыб.

Важную роль дельта играет в гидрологии. В связи с переносом наносов и осаждением в дельте, она способствует образованию новых земельных площадей. Кроме того, дельта может служить естественным регулятором речного стока, поглощая и задерживая часть воды при паводках и снижая риск наводнений.

Однако дельты оказываются уязвимыми перед различными угрозами. Засорение, загрязнение воды, изменение пределов паралельноого отка образуют ряд проблем для дельт. Изменения климата и многие другие факторы могут привести к их уничтожению или деградации.

Чтобы сохранить и восстановить дельты, требуется масштабная экологическая работа, включающая в себя мониторинг состояния и устойчивости дельт, разработку мер по охране и восстановлению их экосистем, осуществление контроля загрязнения и обеспечение устойчивого использования ресурсов.

Примеры дельт	Местоположение
Дельта Нила	Египет
Дельта Миссисипи	США
Дельта Волги	Россия